材料力学(金忠谋)第六版答案第10章

习 题14-1 195-2c 型柴油机连杆大头螺栓如图示，工作时所受最大拉力P max =9.58 kN ，P min＝8.71 kN ，螺栓最小直径d =8.5mm 。

试求其应力幅a σ，平均应力m σ和循环特征r ，并作出t -σ曲线。

解:()()MPaA P P A P a a67.7105.814.3412/1071.858.92//623min max =⨯⨯⨯⨯⨯-=-==-σ ()()MPaA P P A P m m161105.814.3412/1071.858.92//623min max =⨯⨯⨯⨯⨯+=+==-σ91.0maxmin ==σσr14-2 某阀门弹簧如图所示，当阀门关闭时,最小工作载荷P min ＝200N ， 当阀门顶开时最大工作载荷P max ＝500N 。

设簧丝的直径d ＝5mm ，弹簧外径mm D 361=，试求平均应力m τ，应力振幅a τ，循环特性r ，并作出t -τ曲线。

解:4.14/==d D C∴()()09.134/24=-+=C C K∴MPadD P Km m 28010514.31023625002001609.12/169333=⨯⨯⨯⨯+⨯⨯==--πτMPadD P Ka a 12010514.31023622005001609.12/169333=⨯⨯⨯⨯-⨯⨯==--πτ4.0/max min ==P P r14-3 阶梯轴如图所示。

材料为铬镍合金钢，MPa b 920=σ，MPa 4201=-σ，MPa 2501=-τ。

轴的尺寸d =40mm ，D ＝50mm ，r =5mm 。

试计算弯曲和 扭转时的有效应力集中系数和尺寸系数。

解: 由已知条件25.1=d D ，125.0=dr查图表14-12（c ）可得57.1=σK 由图表14-16，当d=40mm 时对MPa b 500=σ的钢材，84.0=σε 对MPa b 1200=σ的钢材，73.0=σε 对MPa b 920=σ的钢材， ()774.073.084.05001200920120073.0=-⨯--+=σε14-4 图示为一货车车轴，轴上的载荷P =110kN ，轴的材料为碳钢，MPa b 550=σ，MPa 2401=-σ，mm a 118=，mm l 1435=，mm d 133=，mm D 146=，mm r 20=，轴表面经磨削加工，规定安全系数8.1=n 。

衿解：在材料相同、截面相同的情况下，螆相当长度最小的压杆的临界力最大。

For personal use only in studyand research; not for commercial use薄第十章压杆稳定羃第十章答案蚈10.1图示为支撑情况不同的圆截面细长杆 ，各杆直径和材料相同，哪个杆的临界力最大。

蚁（a ） U =2 l =2l '' '■'艿（b ） J l =1 1.3l =1.3l羈（c ） T =0.7 1.7l =1.19l腿（d ） J l =0.5 2l =l ，临界力最大。

莃10.2图示为支撑情况不同的两个细长杆，两个杆的长度和材料相同，为使两个压杆的临 界力相等，b 2与b 1之比应为多少: 1 ）膈蕿解:芈 F cr 「(1) 二2EI 2(2I)2 (2)蚂令(1) = (2): I 2 12莈解: -2EI2 = Feos J (2lJ 2(1) (2)b 2 = 2b 薂10.3铰接结构ABC 由截面和材料相同的细长杆组成， 若由于杆件在 ABC 平面内失稳而引起破坏，试确定荷载F 为最大时(两个杆同时失稳时)的0 (0v 0< TI /2)角。

(带arctan (1/3)=18.44 ° )-2EI(2®薄10.4图示压杆，型号为 20a 工字钢，在xoz 平面内为两端固定，在 xoy 平面内为一端固 定，一端自由，材料的弹性模量 E = 200GPa ,比例极限 萨200MPa ，试求此压杆的临 界力。

(F c r = 402.2kN )膂解：(1)柔度计算 查表知:例极限OP = 200MPa ，屈服极限 数n st =2.5，试校核结构是否安全。

OS= 240MPa ，强度安全系数n=2，规定的稳定安全系 （P cr =45.2kN,压杆安全，拉(y= 67.52MPa,安全) 袅解：（1）受力分析： AN 杆受拉力F N1=1.414F=21.21Kn肃BC 杆受压力F N2=F=15Kn聿（2）强度计算:［刁= 120MPa -2 F N1 3 4 21.1 10■: 2023 4 15 10 JI 202= 67.5MPa :::［刁，强度够;= 47.7MPa 十］ 上=81.5mm,y 21.1mm ,A = 3558mm螇(2)xoz 平面内失稳： * = 竺 =2000二94.78i y 21.1蒄为中柔度杆，二⑴=a —b \ =197.8MPa, F cr = ；： cr A = 704kN (2)膂(2)xoy 平面内失稳： Z =，2~ = 8000 =98.16i Z 81.5葿为中柔度杆， 二r =a-b z =194.1MPa, F cr 二二cr A = 690kN袇10.5结构如图，二杆的直径均为 d=20mm ，材料相同，材料的弹性模量 E = 210GPa ,比= 100, 0a -；「S 2E (1)=60肇（3）稳定性分析:1 ,3 巾732F,F N2 2、3F 13 螁(2)稳定性分析：膀取［F ］=F2=47.6kNI = 1m , d = 40mm ，材料的 q = 240MPa ，直线经验公， q r =,一端自由， 圆形截面杆长为 0.8I ，试确 入圆=3.2( d /d),矩形截面杆临界应力小，| F 羅解：对细长杆， cr 蒃矩形: i r 荿圆形： 二2E (1.2d) d V 121.2d二 2EI (7) 「— 3.46』 r i r d叫0.81)4'薁满足稳定性条件 肂10.6图示二圆截面压杆的长度、直径和材料均相同，已知 弹性模量E = 200GPa ,比例极限q p = 200MPa ，屈服极限 304-1.12入(MPa)，试求二压杆的临界力。

第一章 绪论1-1 求图示杆在各截面（I ）、（II ）、（III ）上的力，并说明它的性质．解：（a ）I-I 截面： N = 20KN (拉)II-II 截面： N = -10KN （压）III-III 截面： N = -50KN (压)（b ）I-I 截面： N = 40KN （拉）II-II 截面： N = 10KN (拉)III-III 截面： N = 20KN （拉）1-2 已知P 、M 0、l 、a ，分别求山下列图示各杆指定截面（I ）、(II)上的力解：（a ）：（I ）截面：力为零。

（II ）截面：M = Pa （弯矩）Q = -P （剪力）（b ）：（I ）截面：θsin 31P Q =θsin 61PL M = （II ）截面：θsin 32P Q = θsin 92PL M =（c ）：（I ）截面：L M Q 0-= 021M M = （II ）截面：L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙，试求（1）支座反力，（2）1-1、2-２、3-3各横截面上的力（1-1，2-2是无限接近集中力偶作用点．）解：10110=⨯=A Y （KN ）1055.110-=+⨯-=A M （KN-M ）（1-1） 截面：10110=⨯=Q （KN ）521110-=⨯⨯-=M （KN-M ） （2-2）截面：10=Q （KN ）055=-=M （KN-M ）（2-3）截面：10=Q （KN ）551110-=+⨯⨯-=M （KN-M ）1-4 求图示挂钩AB 在截面 1-1、2-2上的力．解：（1-1）截面：P N 32=a P M ⋅=43 （2-2）截面：P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座，B 端用拉杆约束住，求拉杆的力和在梁1-1截面上的力．解：（1）拉杆力T ：1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT （KN ）（拉） （2）（1-1）截面力：Q 、N 、M ：5030sin -=-=οT Q （KN ）6.8630cos -=-=οT N （KN ）（压）()2550.030sin =⨯=οT M （KN-M ）1-6 一重物 P ＝10 kN 由均质杆 AB 及绳索 CD 支持如图示，杆的自重不计。

材料力学(金忠谋)第六版答案第14章第十三章 动载荷13－1 铸铁杆AB 长m l 8.1=，以等角速度绕垂直轴O －O 旋转如图示。

已知铸铁的比重3/74m kN =γ，许用拉应力[]MPa 40=σ，材料的弹性模量E ＝160 Gpa 。

试求此杆的极限转速，并计算此杆在转速m r n /100=时的绝对伸长。

解： （1） 极限转速m rn s s l g l g A A Ndl gA dr r qd r Nd x r gAdr ma r qd x r a jx dl n n 1092260137.114175.130799.010*******.92)2(][2][)2(21][)2(21)()()()()(235222222222====⨯⨯⨯⨯⨯=≤≤≤======⎰πωωγσωσωγσσωγωγω（2） 当n ＝1000m rcm m Eg l r EA r Nd l s n l 0252.01052.28.91016039.072.104107423)2(2)(2172.1046010002602492233220=⨯=⨯⨯⨯⨯⨯⨯⨯===∆=⨯==-⎰ωππω（2）吊索： MPa A P d d 55.2105276.14max=⨯==-σ13－3 轴上装一钢质圆盘，盘上有一圆孔。

若轴与盘以s140=ω的匀角速度旋转，论求轴内由这一圆孔引起的最大正应力。

解：23max max 22225.1212.021*********.01060041411060064003.03.047800640404.0mMN W M mN L P N Na gA ma P s m r a z d d d d n n d n =⨯⨯==⋅=⨯⋅===⨯⨯⨯⨯=⋅⋅⋅===⨯==πσπδγω13－4 飞轮轮缘的平均直径D ＝1.2m ，材料比重3/72m kN =γ，弹性模量GPa E 200=，轮缘与轮幅装配时的过盈量mmD2.0=∆，若不计轮相的影响，求飞轮允许的最大转速。

习题2-1一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量E0.10 10 5MPa．如不计柱自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形．解：（1）轴力图（2） AC 段应力100 10 3 2.5 10 6 a 2.5 a0.2 2CB 段应力260 10 3 6.5 10 6 a 6.5a0.2 2（ 3）AC 段线应变0.12.5 2.510 4N- 图105CB 段线应变0.16.5 6.510 4 105（ 4）总变形 2.510 4 1.5 6.5 10 4 1.5 1.35 103 m2-2图 (a) 所示铆接件，板件的受力情况如图（ｂ）所示．已知：P＝ 7 kN ， t＝ 0.15cm， b1＝ 0.4cm，b2 =0.5cm， b3=0.6cml 。

试绘板件的轴力图，并计算板内的最大拉应力。

解:（1）轴力图1 7（2） 1310 710 6194.4a0.40.15 22 7310 7 10 20.50.15 230.15 7107 100.6 266311.1a388.9 a 最大拉应力 max3388.9 a2-3 直径为１ cm 的圆杆， 在拉力 P ＝ 10 kN 的作用下， 试求杆内最大剪应力， 以及与横截面夹角为＝ 30o 的斜截面上的正应力与剪应力。

解 :（ 1） 最大剪应力max122 （ 2）30 界面上的应力2 10 10 710663.66a41 d 2121 cos 263.66395.49 a22sin 263.66 sin 3055.13 a22-4 图示结构中 ABC 与 CD 均为刚性梁， C 与D 均为铰接，铅垂力 P ＝ 20kN 作用在 C 铰，若（ 1）杆的直径 d 1=1cm ，（ 2）杆的直径 d 2=2cm ，两杆的材料相同， E ＝ 200Gpa ，其他尺寸如图示，试求（ 1）两杆的应力；（ 2） C 点的位移。

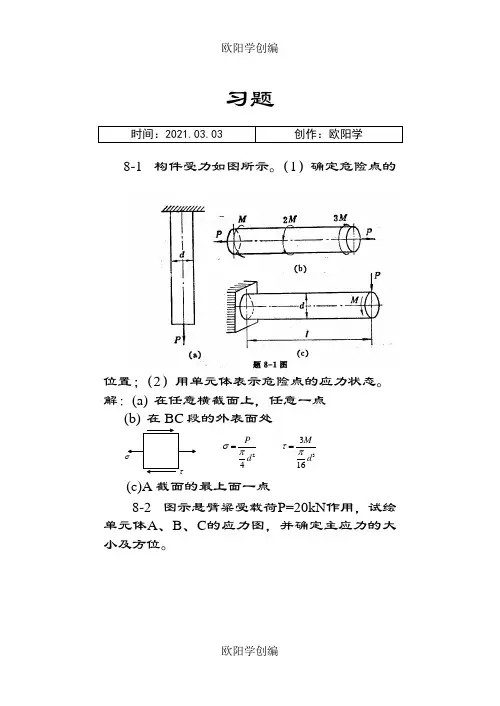
习题时间：2021.03.03 创作：欧阳学8-1 构件受力如图所示。

（1）确定危险点的位置；（2）用单元体表示危险点的应力状态。

解：(a) 在任意横截面上，任意一点24P d σπ=3316M dτπ= τσ (c)A 截面的最上面一点8-2 图示悬臂粱受载荷P=20kN 作用，试绘单元体A 、B 、C 的应力图，并确定主应力的大小及方位。

解：8-3主应力单元体各面上的应力如图所示，试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ，并找出最大剪应力值及方位（应力单位：MPa ）。

解：(a) ()()1212205205cos 2cos 6013.752222MPaασσσσσα+---+-=+=+= 45α= （与120σ=方向夹角）(b)()()()121220102010cos 2cos 135 5.6062222M ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=- 45α= （与1σ方向夹角）或135（与水平方向交角）(c)45α= （与140σ=方向夹角）(d)8-4单元体各面的应力如图示（应力单位为MPa ），试用解析法和图解法计算主应力的大小及所在截面的方位，并在单元体内注明。

解：(a)(b)(c)(d)8-5作出图示单元体的三向应力图，并求出主应力和最大剪应力，画出主单元体。

解：(a) (b) (c ) (d)(e)8-6 已知矩形截面梁某截面上的弯矩和剪力分别为M ＝10kN·m ，FS ＝120kN ，试绘出截面上1、2、3、4各点单元体的应力状态，并求其主应力。

解：8-7在棱柱形单元体的AB 面上以及与ABC 面平行的前后面上（与纸平面平行的面），均无应力作用。

在AC 面和BC 面上的正应力均为-15MPa ，试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。

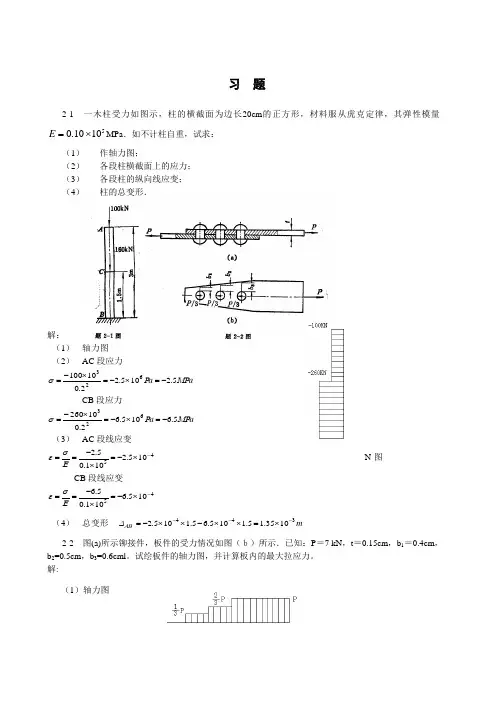
习 题2-1 一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量51010.0⨯=E MPa ．如不计柱自重，试求：（1）作轴力图； （2）各段柱横截面上的应力； （3）各段柱的纵向线应变； （4） 柱的总变形．解：（1） 轴力图（2） AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-= CB 段应力 a a MP P σ5.6105.62.010260623-=⨯-=⨯-=（3） AC 段线应变 45105.2101.05.2-⨯-=⨯-==E σε N-图CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε （4） 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7 kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。

试绘板件的轴力图，并计算板内的最大拉应力。

解:（1）轴力图（2）a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=-a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=- a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max == 2-3 直径为１cm 的圆杆，在拉力P ＝10 kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为α＝30o 的斜截面上的正应力与剪应力。

解:（1） 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- （2） ︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒2-4 图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。

第十一章 变形能法11-1求图示两等直杆的变形能。

已知两杆的抗拉刚度EA 相同。

解：（a ）EAdxN dU 22=lP q =2EIDAlllAll⎰⎰=====llEAlP dx EAl x P dU U x tP qx N 0222262(b)EAl P dx EA l x P U lx P N l 6721)1(2022=⎪⎭⎫⎝⎛+=+=⎰11-2两根圆截面直杆的材料相同，尺寸如图所示，其中一根为等截面杆，另一根为变截面杆，试比较两根杆的变形能。

（各杆自重不计）解：杆（a ）2222242Ed l P dE lP U a ππ=⨯= 杆（b ）22222287424)2(4283EdlP d E l P d E lP U b πππ=⨯⨯+⨯⨯= 故716=b a U U11-3图示桁架各杆材料相同，截面面积相等，试求在P 力作用下，桁架的变形能。

解：支反力2P R R P R B AyAx ===各杆的轴力和变形能如表所示故珩架的变形能为EA lP EA l P Ui U i 2251957.04122=+==∑=11-4 试计算图示各杆的变形能。

(a) 轴材料的剪切弹性模量为G ，1223d d =； (b) 梁的抗弯刚度EI ，略去剪切变形的影响。

解：（a ）m M mM n n ==211421P GJ l m U =2422P GJ lm U = 41321d J P π=41423206.5322d d J P ππ==412216.9d G lm U U U π=+= (b) 支反力 lM R R B A == 111x l M x R M A -=-= （301l x ≤≤） 222x l M x R M B == （3202l x ≤≤）⎰⎰=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+=3202222130211822l l BCAC EJl M dx EJ x l M dx FJ x l M U U U11-5 试求图示悬臂梁的弹性变形能，梁的抗弯刚度为EI ，并求自由端的挠度。

材料力学(金忠谋)第六版答案第10章第十章组合变形的强度计算10-1图示为梁的各种截面形状，设横向力P 的作用线如图示虚线位置，试问哪些为平面弯曲？哪些为斜弯曲？并指出截面上危险点的位置。

（a）(b) (c) (d)斜弯曲平面弯曲平面弯曲斜弯曲弯心（）（）弯心弯心（）（）斜弯曲 弯扭组合平面弯曲 斜弯曲 “×”为危险点位置。

10-2矩形截面木制简支梁AB ，在跨度中点C 承受一与垂直方向成ϕ＝15°的集中力P ＝10 kN 作用如图示，已知木材的弹性模量MPa100.14⨯=E 。

试确定①截面上中性轴的位置；②危险截面上的最大正应力；③C 点的总挠度的大小和方向。

解：66.915cos 10cos =⨯== ϕP P y KN 59.215sin 10sin =⨯== ϕP P z KN4310122015=⨯=z J4cm3310cm Wz=10-3 矩形截面木材悬臂梁受力如图示，P 1＝800 N ，P 2＝1600 N 。

材料许用应力[σ]=10MPa ，弹性模量E ＝10GPa ，设梁截面的宽度b 与高度h 之比为1：2。

①试选择梁的截面尺寸；②求自由端总挠度的大小和方向。

解：（I ）6.112m ax=⨯=P Mz KN6.120max=⨯=P M y KN322326)2(6bb b bh W z ===33231626bb bh W y ===hbP 220cm15cm[]633133323m ax m ax m ax1010106.1106.1⨯=≤⨯+⨯=+=σσb b W M W M Y y z zb = 9 cm ， h = 18 cm （II）cm m EJ P EJ P EJ P f zz y 97.11097.11213132223232231=⨯⎪⎪⎭⎫⎝⎛⨯⨯+⨯+⎪⎪⎭⎫ ⎝⎛⨯=-1.81,305.095.1tan ===ααy z f f10-4简支梁的受力及横截面尺寸如图示。

材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m －m 截面上A 点的正应力和危险截面上最大正应力。

题 6-1图解：（a ）m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ （b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。

4解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。

第10章 疲劳强度的概念思考题10-1 什么是交变应力？举例说明。

答 随时间作周期性变化的应力称交变应力。

如下图所示的圆轴以角速度ω匀速转动，轴上一点A 的位置随时间变化，从A 到A ′，再到A ′′，再到A ′′′，又到A 处，如此循环往复。

轴上该点的正应力A σ也从0到，再到0，再到，又到0，产生拉压应力循环。

该点的应力即为交变应力。

+max σ−max σ10-2 疲劳失效有何特点？疲劳失效与静载失效有什么区别？疲劳失效时其断口分成几个区域？是如何形成的？答 （1）疲劳失效时的应力σ远低于危险应力u σ（静载荷下的强度指标）；需要经过一定的应力循环次数；构件（即使是塑性很好的材料）破坏前和破坏时无显著的塑性变形，呈现脆性断裂破坏特征。

（2）疲劳失效的最大工作应力σ远低于危险应力u σ；静载失效的最大工作应力σ为危险应力u σ。

（3）疲劳失效时其断口分成2个区域：光滑区域和颗粒状粗糙区域。

（4）构件在微观上，其内部组织是不均匀的。

在足够大的交变应力下，金属中受力较大或强度较弱的晶粒与晶界上将出现滑移带。

随着应力变化次数的增加，滑移加剧，滑移带开裂形成微观裂纹，简称“微裂纹”。

另外，构件内部初始缺陷或表面刻痕以及应力集中处，都可能最先产生微裂纹。

这些微裂纹便是疲劳失效的起源，简称“疲劳源”。

微裂纹随着应力交变次数的继续增加而不断扩展，形成了裸眼可见的宏观裂纹。

在裂纹的扩展过程中，由于应力交替变化，裂纹两表面的材料时而互相挤压、时而分离，这样就形成了断口表面的光滑区。

宏观裂纹继续扩展，致使构件的承载截面不断被削弱，类似在构件上形成尖锐的“切口”。

这种切口造成的应力集中，使局部区域内的应力达到很大数值。

最终在较低的应力水平下，由于累积损伤，致使构件在某一次载荷作用时突然断裂。

断口表面的颗粒状区域就是这种突然断裂造成的，所以疲劳失效的过程可以理解为裂纹产生、扩展直至构件断裂的一个过程。

10-3 什么是对称循环？什么是脉冲循环？ 答 对称循环是指最大应力与最小应力大小相等，正负号相反的应力循环。