1.4 菲涅耳公式

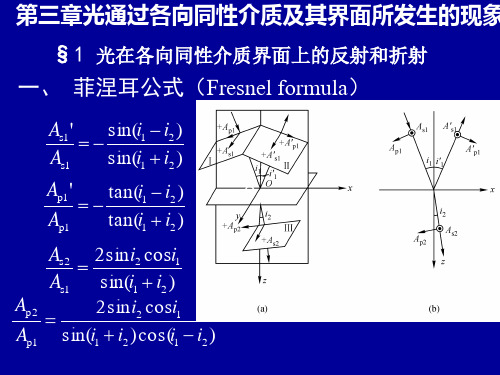
§1-6 菲涅耳公式一．菲涅耳公式电磁波通过不同介质的分界面时会发生反射和折射，在电动力学中将讲到入射、反射和折射三束波在分界面上振幅的大小和方向之间的关系，这一关系可由菲涅耳公式表达出来，上节提到的在反射过程中发生的半波损失问题，就可以用这个公式来解释，这一公式对以后讲到的许多光学现象，都能圆满地加以说明。

菲涅耳公式的内容说明如下：在任何时刻，我们都可以把入射波、反射波和折射波的电矢量分成两个分量，一个平行于入射面，另一个垂直于入射面。

有关各量的平等分量与垂直分量依次用指标P 和S 来表示。

以1i 、'1i 和2i 分别表示入射角、反射角和折射角，它们确定了各波的传播方向（在大多数情况下，只要注意各波的磁场矢量即可，因为知道了各个波的传播方向，各波的磁场矢量就可按右螺旋关系确定）。

以1A 、'1A 和2A 来依次表示入射波、反射波和折射波的电矢量的振幅，它们的分量相应就是1P A 、1'P A 、2P A 和1s A 、1's A 、2s A 。

由于三个波的传播方向各不相同，必须分别规定各分量的某一个方向作为正方向，这种规定当然是任意的。

但是只要在一个问题材的全部讨论过程中始终采取同一种正方向的选择，由此得到的各个关系式就具有普遍的意义，(a)(b)(图1-16)图1-16中xy 平面为两介质的分界面，z 轴为法线方向，xz 平面为入射面，规定电矢量的s 分量以沿着y +方向的为正，这对于入射、反射和折射三个波都相同，图中III II I 、、三个面依次表示入射、反射和折射三个波的波面。

电矢量的P 分量沿着这三个波面与入射面的交线，它们的正方向分别规定为如图1-16)()(b a 、所示，且S 分量、P 分量和传播方向三者构成右螺旋关系。

在传播过程中，电矢量的方向是在不断变化的，我们所注意的仅是在反射、折射过程这一瞬时的变化，所以菲涅耳公式所表示的有关各量的方向都是指紧靠两介质分界面O 点处而言的（在图中为清楚起见，将通过O 点的三个波面画III II I 、、画在离开O 点较远之处）。

菲涅尔公式是描述光在两种介质交界面上反射和折射现象的一组公式，由法国物理学家菲涅尔在19世纪提出。

该公式包含了入射光线的角度、两种介质的折射率以及反射和折射光线的角度等因素。

菲涅尔公式可以用来计算反射和透射光线的强度和相对方向，是光学研究中非常重要的工具。

它的表达式形式较为复杂，包括两个方程式：一个是描述垂直入射光线的情况，另一个是描述斜入射光线的情况。

具体表达式如下：
垂直入射光线：
反射系数R = ((n1-n2)/(n1+n2))²
透射系数T = 1-R
斜入射光线：
反射系数R = ((n1cosθ1 - n2cosθ2)/(n1cosθ1 + n2cosθ2))²
透射系数T = 1-R
其中，n1和n2表示两种介质的折射率，θ1和θ2表示入射光线和反射/折射光线的夹角（取决于光线从哪种介质入射），cos表示夹角的余弦值。

- 1 -。

菲涅耳公式
费涅耳公式，也称费涅耳定律，它是由德国物理学家威廉·费涅耳在1850年提出的一种物理公式，主要用于研究不同温度下液体的密度和比重。

它可以用来计算一定温度下液体的密度和比重，也可以用来研究液体的物理性质。

费涅耳公式的表达式为：ρ=ρ0（1-α（t-t0）），其中ρ表示温度t时的液体密度，ρ0表示温度t0时的液体密度，α表示温度变化时的热膨胀系数。

这个公式表明，任何液体的温度变化都会导致其密度和比重发生变化。

费涅耳公式也可以用来研究液体的物理性质，因为液体温度的变化会对液体的物理性质产生影响。

例如，当液体温度升高时，液体的粘度和抗拉强度会降低；当液体温度升高时，液体的比表面张力会增加。

费涅耳公式的发现对于物理学的发展有着重要的意义，它给出了不同温度下液体的密度和比重之间的关系，使得研究液体的物理性质变得更加精确和客观。

它也为控制液体的性质提供了有效的方法，使得很多工业生产变得更加高效和可控。

总之，费涅耳公式是一个重要的物理学公式，它为液体的研究和控制提供了重要的理论基础。

菲涅尔积分公式
菲涅尔积分公式是光学和工程学中非常重要的公式之一，它用于描述光在两种不同介质之间反射和折射的过程。

这个公式是由物理学家和数学家奥古斯特·菲涅尔在19世纪初提出的，它基于光的波动理论，描述了光波在两种不同介质之间的传播行为。

菲涅尔积分公式包含两个部分：反射系数和折射系数。

反射系数用于描述光在两种不同介质之间的反射行为，而折射系数用于描述光在两种不同介质之间的折射行为。

这两个系数都与入射角、反射角和折射角有关，同时也与两种介质的折射率有关。

反射系数和折射系数的具体形式如下：
1. 反射系数R = (n2 * sinθi - n1 * sinθt) / (n2 * sinθi + n1 * sinθt)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和反射角。

2. 折射系数T = 2 * n1 * sinθi / (n2 * sinθt + n1 * sinθi)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和折射角。

在光学和工程学中，菲涅尔积分公式被广泛应用于计算光在各种不同介质之间的反射和折射行为。

这个公式对于光学设计、成像系统分析、光学仪器制造等领域非常重要。

除了菲涅尔积分公式外，还有许多其他公式和定理用于描述光的行为，例如斯涅尔定律、反射定理、折射定理等。

这些公式和定理都是基于光的波动理论或量子理论，是光学和工程学领域的重要工具。

综上所述，菲涅尔积分公式是一个重要的公式，用于描述光在两种不同介质之间反射和折射的行为。

它基于光的波动理论，包含反射系数和折射系数两个部分，对于光学设计和工程学领域非常重要。

菲涅耳公式
菲涅耳公式，又称为“菲涅耳现象”，是由瑞士天文学家哈维·菲涅耳（Johannes Kepler）所提出的一种数学定律。

菲涅耳公式描述了两个相邻星体之间的关系，即它们之间的距离是衡量它们之间的强度的重要因素。

菲涅耳公式可以用以下方程式表示：F = Gm1m2/r^2，其中F是两个物体之间的引力，m1和m2是两个物体的质量，G是万有引力常数，r是两个物体之间的距离。

该公式表明，两个物体之间的引力是由它们的质量以及它们之间的距离决定的。

菲涅耳公式是物理学和天文学领域中最重要的数学定律之一，它描述了两个物体之间的引力，这种引力是由它们的质量和它们之间的距离决定的。

菲涅耳公式对于解释宇宙中星体之间的运动有着重要的作用，它给天文学家和物理学家带来了深刻的启发，它也是天体力学理论上最有用的数学公式之一。

菲涅耳公式可以应用于多种情况，如行星的轨道等。

它也可用于研究太阳系的稳定性，它的应用非常广泛，甚至可以用来计算地球与月球之间的引力。

总之，菲涅耳公式是物理学和天文学领域中一个重要的数学定律，它描述了两个物体之间的引力，这种引力是由它们的质量和它们之
间的距离决定的，它也是天体力学理论上最有用的数学公式之一，广泛应用于多种情况，如行星轨道等。

实验名称 菲涅尔公式的认识一、实验目的:加深理解菲涅尔公式，对给出的反射波或折射波与入射波振幅的相对变化进行分析，以及对相位变化进行分析。

二、实验原理:任一方位振动的光矢量E 都可以分解成互相垂直的两个分量称平行于入射面振动的分量为光矢量的p 分量，记为EP 。

称垂直于入射面振动的分量为光矢量的s 分量，记为ES 。

1.菲涅耳公式:表示反射波、折射波与入射波的振幅和位相关系。

（1）S 波（垂直于入射面分量）的菲涅耳公式s r ——S 波的振幅反射系数 s t ——S 波的振幅透射系数（2）P 波（平行于入射面分量）的菲涅耳公式p r ——P 波的振幅反射系数 p t ——P 波的振幅透射系数2.光从光疏介质入射到光密介质（如空气射向玻璃）当 时，即垂直入射时， 都不为零，表示存在反射波和折射波。

当 时，即掠入射时， 即没有折射光波。

s t 、p t 随1θ的增大而减小；s r 随1θ的增大而增大，直到等于1；221122112121s 1s 1s n n n n A A r θθθθθθθθcos cos cos cos )sin()sin('+-=+--==2211112121s 1s 2s n n n 22A A t θθθθθθθcos cos cos )sin(sin cos +=+==211221122121p 1p1p n n n n tg tg A A r θθθθθθθθcos cos cos cos )()('+-=+-==211211212112p1p 2p n n n 22A A t θθθθθθθθθcos cos cos )cos()sin(cos sin +=-+==p s p s t t r r 、、、01=θ901=θ0t t 1r r p s p s ====,p r 值在() 902B B 1=+=θθθθ时，有0r p =，即反射光波中没有p 波，只有s 波，产生全偏振现象。

斯涅耳定律和菲涅耳公式
首先我们来看看斯涅耳定律。

斯涅耳定律是描述声音在不同介质中传播时的规律的定律。

它指出，当声音由一个介质传播到另一个介质时，入射角、折射角和介质的声速之间存在着一定的关系。

斯涅耳定律的数学表达式为，n1sin(θ1) = n2sin(θ2)，其中n1和n2分别为两个介质的声速，θ1和θ2分别为声波在两个介质中的入射角和折射角。

斯涅耳定律的发现为我们理解声音在不同介质中传播的规律提供了重要的理论基础，也为声波的传播和应用提供了重要的指导。

接下来我们来看看菲涅耳公式。

菲涅耳公式是描述光在介质中折射和反射的规律的公式。

它包括了反射角、折射角和介质的折射率之间的关系。

菲涅耳公式的数学表达式为，(n1sin(θ1)) =
(n2sin(θ2))，其中n1和n2分别为两个介质的折射率，θ1和θ2分别为光线在两个介质中的入射角和折射角。

菲涅耳公式的发现为我们理解光在介质中传播的规律提供了重要的理论基础，也为光的传播和应用提供了重要的指导。

斯涅耳定律和菲涅耳公式的发现和应用为我们理解和利用声音和光的传播提供了重要的理论基础。

它们的应用不仅帮助我们解释
自然现象，还为声波和光线的传播和应用提供了重要的指导。

因此，斯涅耳定律和菲涅耳公式在物理学中具有非常重要的意义。