菲涅耳公式推导

fresnel公式【原创实用版】目录1.Fresnel 公式的定义与含义2.Fresnel 公式的应用领域3.Fresnel 公式的推导过程4.Fresnel 公式的实际应用案例5.Fresnel 公式的局限性与未来发展方向正文【1.Fresnel 公式的定义与含义】Fresnel 公式，又称菲涅耳公式，是由法国物理学家奥古斯特 - 路易 - 菲涅耳（Augustin-Louis Fresnel）于 19 世纪初提出的一种描述光的传播和反射、折射等现象的数学公式。

Fresnel 公式主要描述了光在两种介质之间传播时，反射光和折射光的振幅比值关系。

这一公式在物理学、光学等领域具有重要的理论意义和应用价值。

【2.Fresnel 公式的应用领域】Fresnel 公式在多个领域有广泛的应用，包括但不限于：- 光学领域：Fresnel 公式可以用于解释和预测光的反射、折射等现象，对于光学元件的设计和制造具有重要意义。

- 通信领域：Fresnel 公式在光通信中起到关键作用，例如在光纤通信系统中，通过 Fresnel 公式可以计算光信号在光纤中的传播特性。

- 物理学领域：Fresnel 公式为研究光的基本性质提供了理论基础，有助于我们深入理解光的传播规律。

【3.Fresnel 公式的推导过程】Fresnel 公式的推导过程相对简单，假设光在两种介质之间传播，分别用 A 和 B 表示两种介质，光的入射角为θi，折射角为θr。

设入射光的振幅为 A1，折射光的振幅为 A2，反射光的振幅为 A"1。

根据波动理论，可以得到以下关系式：A1 = A2 * cosθr / cosθiA"1 = A1 * (1 - cosθr / cosθi)通过上述公式，我们可以得到 Fresnel 公式：A"1 / A1 = (1 - cosθr / cosθi)【4.Fresnel 公式的实际应用案例】Fresnel 公式在现实生活中有很多应用案例，例如在光学镜头设计中，通过 Fresnel 公式可以优化镜头的性能，减少光的反射损失，提高成像质量。

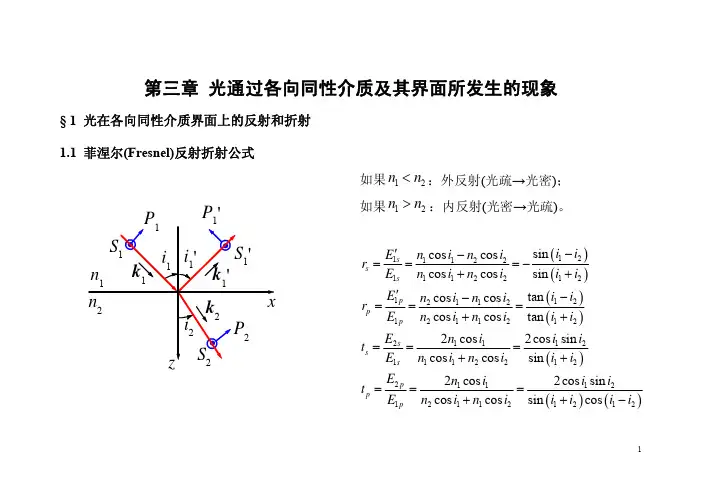
§1-6 菲涅耳公式一．菲涅耳公式电磁波通过不同介质的分界面时会发生反射和折射，在电动力学中将讲到入射、反射和折射三束波在分界面上振幅的大小和方向之间的关系，这一关系可由菲涅耳公式表达出来，上节提到的在反射过程中发生的半波损失问题，就可以用这个公式来解释，这一公式对以后讲到的许多光学现象，都能圆满地加以说明。

菲涅耳公式的内容说明如下：在任何时刻，我们都可以把入射波、反射波和折射波的电矢量分成两个分量，一个平行于入射面，另一个垂直于入射面。

有关各量的平等分量与垂直分量依次用指标P 和S 来表示。

以1i 、'1i 和2i 分别表示入射角、反射角和折射角，它们确定了各波的传播方向（在大多数情况下，只要注意各波的磁场矢量即可，因为知道了各个波的传播方向，各波的磁场矢量就可按右螺旋关系确定）。

以1A 、'1A 和2A 来依次表示入射波、反射波和折射波的电矢量的振幅，它们的分量相应就是1P A 、1'P A 、2P A 和1s A 、1's A 、2s A 。

由于三个波的传播方向各不相同，必须分别规定各分量的某一个方向作为正方向，这种规定当然是任意的。

但是只要在一个问题材的全部讨论过程中始终采取同一种正方向的选择，由此得到的各个关系式就具有普遍的意义，(a)(b)(图1-16)图1-16中xy 平面为两介质的分界面，z 轴为法线方向，xz 平面为入射面，规定电矢量的s 分量以沿着y +方向的为正，这对于入射、反射和折射三个波都相同，图中III II I 、、三个面依次表示入射、反射和折射三个波的波面。

电矢量的P 分量沿着这三个波面与入射面的交线，它们的正方向分别规定为如图1-16)()(b a 、所示，且S 分量、P 分量和传播方向三者构成右螺旋关系。

在传播过程中，电矢量的方向是在不断变化的，我们所注意的仅是在反射、折射过程这一瞬时的变化，所以菲涅耳公式所表示的有关各量的方向都是指紧靠两介质分界面O 点处而言的（在图中为清楚起见，将通过O 点的三个波面画III II I 、、画在离开O 点较远之处）。

菲涅耳公式
费涅耳公式，也称费涅耳定律，它是由德国物理学家威廉·费涅耳在1850年提出的一种物理公式，主要用于研究不同温度下液体的密度和比重。

它可以用来计算一定温度下液体的密度和比重，也可以用来研究液体的物理性质。

费涅耳公式的表达式为：ρ=ρ0（1-α（t-t0）），其中ρ表示温度t时的液体密度，ρ0表示温度t0时的液体密度，α表示温度变化时的热膨胀系数。

这个公式表明，任何液体的温度变化都会导致其密度和比重发生变化。

费涅耳公式也可以用来研究液体的物理性质，因为液体温度的变化会对液体的物理性质产生影响。

例如，当液体温度升高时，液体的粘度和抗拉强度会降低；当液体温度升高时，液体的比表面张力会增加。

费涅耳公式的发现对于物理学的发展有着重要的意义，它给出了不同温度下液体的密度和比重之间的关系，使得研究液体的物理性质变得更加精确和客观。

它也为控制液体的性质提供了有效的方法，使得很多工业生产变得更加高效和可控。

总之，费涅耳公式是一个重要的物理学公式，它为液体的研究和控制提供了重要的理论基础。

隔声屏障菲涅尔数公式
隔声屏障的菲涅尔数公式为：$N = \frac{2}{\lambda}(A + B - d) =
\frac{2\delta}{\lambda} = \frac{\delta f}{170}$，其中λ是声源的波长，f 是声波的频率。

N代表菲涅尔数，Δ表示屏障高度。

根据这个公式，可以通过计算的菲涅尔数N查找到降噪量NR，其中表中的负号表示声线与接收点的连线不与声屏障相交，即声屏障对此连线无遮挡，但声波仍会有衰减。

当$N = 1 \sim 10$的范围内，还可用公式$NR \approx 13 + 10\lg
N(dB)$近似估算。

由于菲涅尔数N与声波频率f成正比，则有声波频率增加一倍，声屏障降噪量大约增加3dB。

以上信息仅供参考，如需获取更多详细信息，建议查阅声学专业书籍或咨询专业人士。

推导菲涅尔公式
菲涅尔公式是用来描述光在介质边界发生反射和折射的现象的公式。

它由奥古斯严·菲涅尔（Augustin-Jean Fresnel）在19世纪初提出，并经过后来的实验验证。

推导菲涅尔公式的过程如下：
1. 首先，考虑光从真空（折射率为n1=1）射入一个不同折射率的介质（折射率为n2）的情况。

设光线入射角为θ1，折射角为θ2。

2. 根据光的波动理论，我们知道光是电磁波，具有垂直于传播方向的电场分量和磁场分量。

这里我们只关注电场分量。

3. 假设入射光的电场分量为E1，反射光的电场分量为E_r，折射光的电场分量为E_t。

4. 根据光的边界条件，可以得到以下两个关系式：
- (1) 入射光的电场分量在入射面上的分量：E1 = Er*cos(θ1) + Et*cos(θ2)
- (2) 入射光的电场分量在入射面上的法向分量：E1*sin(θ1) = Er*sin(θ1) - Et*sin(θ2)
5. 利用折射率的定义，即光在不同介质中的传播速度之比等于折射率之比，可以得到以下关系式：
- (3) n1*sin(θ1) = n2*sin(θ2)
6. 利用这些关系式，我们可以解出反射光的电场分量Er和折射光的电场分量Et与入射光的电场分量E1之间的关系。

7. 最终，通过计算得到的反射光和折射光的电场分量与入射光
的电场分量之比，可以得到反射系数R和透射系数T。

8. 菲涅尔公式就是关于反射系数R和透射系数T的表达式。

需要注意的是，具体的推导过程包含一些复杂的数学计算和光学理论，超出了简单的文字描述范围。

菲涅尔公式的推导过程菲涅尔公式是电磁波在两介质交界处反射和折射的行为的数学描述，它的推导过程相当有趣和具有指导意义。

下面我们将详细讨论菲涅尔公式的推导过程。

假设我们有一束入射电磁波，它以某个角度从介质1射向介质2的边界，我们将波的入射角定义为θ1。

此外，我们知道波的入射角和折射角（波从边界反射或折射出去后，与介质界面的夹角）是相关的，根据折射定律可以得到折射角θ2。

接下来，我们考虑入射波如何在介质界面处发生反射和折射。

当电磁波从介质1射入介质2时，一部分波将被反射回来，同时一部分波将折射进入介质2。

假设反射波的电场振幅为Er，折射波的电场振幅为Et。

为了推导菲涅尔公式，我们将利用边界条件和电磁波的性质。

首先考虑边界条件，边界上的电场分量垂直于介质界面，我们假设介质1和介质2分别为真空和某种线性均匀介质。

根据这些假设，我们可以得到两个边界条件：1. 在介质1与介质2的边界上，电场的切向分量相等，即E1t =E2t。

2. 在介质1与介质2的边界上，电场的法向分量比值等于两个介质的电磁波阻抗之比，即(E1n / E2n) = (Z1 / Z2)。

其中切向分量表示电场平行于界面方向的分量，法向分量表示电场垂直于界面方向的分量，而电磁波阻抗则表示电磁波在特定介质中传播的难易程度，它是介质的电磁参数（电导率和相对介电常数）的函数。

基于这些边界条件，我们可以采用分析法和矢量法来推导出菲涅尔公式。

接下来我们使用矢量法。

首先，由于电场在边界上的切向分量相等，我们可以写出以下方程：Er.sin(θ1) = Et.sin(θ2) --（1）其中sin(θ1)表示入射角的正弦值，sin(θ2)表示折射角的正弦值。

然后，由于电场在边界上的法向分量比值等于两个介质的电磁波阻抗之比，我们可以写出以下方程：(Er.cos(θ1)) / (Et.cos(θ2)) = (Z1 / Z2) --（2）其中cos(θ1)表示入射角的余弦值，cos(θ2)表示折射角的余弦值。

菲涅尔公式的推导过程菲涅尔公式是光学中的重要公式之一，用于计算光的干涉和衍射现象。

该公式的推导过程主要基于惠更斯-菲涅尔原理和边界条件。

下面将详细介绍菲涅尔公式的推导过程。

一、惠更斯-菲涅尔原理惠更斯-菲涅尔原理是光学中的基本原理之一，它描述了波前上的每一点都可以看作是一个次波源，它们发出的球面波会相互干涉，从而形成新的波前。

对于光的干涉和衍射现象，惠更斯-菲涅尔原理是一个重要的理论基础。

在光的干涉和衍射现象中，我们可以将光波的波前看作是由许多个次波源组成的。

对于一个点光源，它的波前可以看作是由许多个点组成的。

每个点都可以看作是一个次波源，它们发出的球面波会相互干涉，从而形成新的波前。

对于两个相邻的点光源，它们发出的球面波会在空间中相遇。

当这两个球面波的相位相同时，它们会相互增强，形成明亮的区域；当相位相反时，它们会相互抵消，形成暗的区域。

这种相位相同和相位相反的情况会导致光的干涉现象。

对于一个衍射孔，它可以看作是一个由许多个点组成的次波源。

每个点都可以看作是一个次波源，它们发出的球面波会相互干涉，从而形成新的波前。

当这些球面波在空间中相遇时，它们会产生加强或抵消的效果，这种效果会导致光的衍射现象。

二、边界条件边界条件是指在两个不同介质的分界面上，光的振幅、相位和偏振态等物理量的变化规律。

在光的干涉和衍射现象中，边界条件是非常重要的。

对于一个折射率为n的介质，当一束光线从介质1射向介质2时，光的折射定律可以表示为：n1 * sin(θ1) = n2 * sin(θ2)其中，n1和n2分别为介质1和介质2的折射率，θ1和θ2分别为入射角和折射角。

这个公式表示了光的折射定律，也可以用来描述光的反射定律。

对于一个反射面，当一束光线从介质1射向介质2时，光的反射定律可以表示为：n1 * cos(θ1) = n2 * cos(θ2)其中，n1和n2分别为介质1和介质2的折射率，θ1和θ2分别为入射角和折射角。

菲涅尔衍射公式与基尔霍夫衍射公式的推导
与比较
菲涅尔衍射公式和基尔霍夫衍射公式都描述了光波通过一个狭缝或孔径时的衍射现象，但它们的推导和适用条件有所不同。

菲涅尔衍射公式是根据菲涅尔衍射理论推导出来的，适用于衍射角比较大的情况。

菲涅尔衍射公式表达为：
I = (A/λ) * sin(θ)^2
其中，I表示在角度θ处的衍射强度，A是狭缝或孔径的宽度，λ是光波的波长。

基尔霍夫衍射公式则是根据基尔霍夫衍射理论推导得到的，适用于衍射角比较小的情况。

基尔霍夫衍射公式表达为：
I = (A^2 * sin(πa sin(θ) / (πa sin(θ))^2) * (sin(πb sin(θ)) / (πb sin(θ))^2))^2
其中，A是狭缝或孔径的宽度，a和b分别表示狭缝或孔径在x和y方向的宽度，θ是衍射角。

总体来说，菲涅尔衍射公式适用于衍射角比较大的情况，而基尔霍夫衍射公式适用于衍射角比较小的情况。

在实际应用中，需要根据具体情况选择合适的衍射公式来进行计算。

另外，需要注意的是，菲涅尔衍射公式和基尔霍夫衍射公式都是近似公式，在某些情况下可能会存在误差，需要谨慎使用。

菲涅尔积分公式
菲涅尔积分公式是光学和工程学中非常重要的公式之一，它用于描述光在两种不同介质之间反射和折射的过程。

这个公式是由物理学家和数学家奥古斯特·菲涅尔在19世纪初提出的，它基于光的波动理论，描述了光波在两种不同介质之间的传播行为。

菲涅尔积分公式包含两个部分：反射系数和折射系数。

反射系数用于描述光在两种不同介质之间的反射行为，而折射系数用于描述光在两种不同介质之间的折射行为。

这两个系数都与入射角、反射角和折射角有关，同时也与两种介质的折射率有关。

反射系数和折射系数的具体形式如下：
1. 反射系数R = (n2 * sinθi - n1 * sinθt) / (n2 * sinθi + n1 * sinθt)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和反射角。

2. 折射系数T = 2 * n1 * sinθi / (n2 * sinθt + n1 * sinθi)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和折射角。

在光学和工程学中，菲涅尔积分公式被广泛应用于计算光在各种不同介质之间的反射和折射行为。

这个公式对于光学设计、成像系统分析、光学仪器制造等领域非常重要。

除了菲涅尔积分公式外，还有许多其他公式和定理用于描述光的行为，例如斯涅尔定律、反射定理、折射定理等。

这些公式和定理都是基于光的波动理论或量子理论，是光学和工程学领域的重要工具。

综上所述，菲涅尔积分公式是一个重要的公式，用于描述光在两种不同介质之间反射和折射的行为。

它基于光的波动理论，包含反射系数和折射系数两个部分，对于光学设计和工程学领域非常重要。

菲涅耳公式推导:
菲涅耳公式是描述入射波与反射波，入射波与透射波振幅关系的式子。

由于自然光可以 等效为偏振面相互垂直的两个线偏振光的叠加，即任意平面电磁波可以等价为其电场矢量相互垂直的两个线偏振波的叠加。

故下面只分别推导电场强度E 垂直入射面和E 平行入射面时的两种情况即可。

1.1 电场强度E 垂直入射面的情况
设两种不同绝缘介质的介电常数和磁导率分别为1ε，1μ和2ε ，2μ。

取如图1所示的坐标。

分界面为z=0的平面，电磁波的入射面为y=0的面。

入射波电场强度只有y 分量。

波动光学中的菲涅尔公式推导波动光学是研究光的传播和相互作用的学科，其中菲涅尔公式是波动光学中的重要公式之一。

本文将对菲涅尔公式的推导进行讨论。

菲涅尔公式是描述光在两个介质之间传播时的反射和折射现象的公式。

它由法国物理学家奥古斯丁·菲涅尔于19世纪初提出，并成为波动光学的基础。

菲涅尔公式的推导基于麦克斯韦方程组和边界条件。

首先，我们需要了解光在介质中的传播方式。

光是一种电磁波，其传播速度和方向受到介质折射率的影响。

当光从一个介质传播到另一个介质时，它会发生折射和反射。

折射是光线改变传播方向的现象，而反射是光线从界面上弹回的现象。

为了推导菲涅尔公式，我们先考虑光从真空进入一个介质的情况。

设光的入射角为θ1，折射角为θ2，光的波长为λ。

根据菲涅尔公式，反射光的振幅与入射光的振幅之比为：r = (n1cosθ1 - n2cosθ2) / (n1cosθ1 + n2cosθ2)其中，n1和n2分别是真空和介质的折射率。

折射光的振幅与入射光的振幅之比为：t = (2n1cosθ1) / (n1cosθ1 + n2cosθ2)接下来，我们来推导这些公式。

首先，根据麦克斯韦方程组，可以得到入射光和反射光的电场分量分别为：Ei = E0e^(i(k1x - ωt))Er = -E0re^(i(k1x + ωt))其中，E0是入射光的振幅，k1是入射光的波矢，ω是角频率。

反射光的振幅与入射光的振幅之比r可以通过比较入射光和反射光的电场分量得到。

接下来，考虑光的传播方向。

根据光的传播方向和入射角度，可以得到入射光和反射光的波矢分量分别为：k1x = k1sinθ1k1z = k1cosθ1k2x = k2sinθ2k2z = k2cosθ2其中，k2是折射光的波矢。

根据光的传播方向和波矢分量，可以得到入射光和反射光的电场分量在界面上的分布情况。

接下来，考虑边界条件。

根据边界条件，入射光和反射光的电场分量在界面上必须连续。

菲涅尔反射公式
菲涅尔反射公式（全称叫做菲涅尔散射定律）由19世纪末的著名物理学家安德烈·菲涅尔提出。

它描述了由任何一个点发出的光被另一个介质中的物质反射或散射出去的情况。

公式表达为：
I=I0*((n*cosθi)^2)/(1+(n-1)^2*(tanθi)^2)
其中，I代表所得到的反射亮度，I0代表光源亮度，n是介质材料的折射率，θi代表入射角。

菲涅尔散射定律是量子物理学领域中重要的散射理论，它是对矫正非直射性成像及光晕、光斑等散射现象的工程分析极为重要的基础理论。

菲涅尔反射公式不仅在天文学、光学、材料科学、仪器科学、生物学仪器测量方面都得到广泛的应用，而且还在军事、航空等领域起着重要作用。

菲涅尔反射公式也被称为菲涅尔反射定律。

它是通过实验证明而被得出的事实，即当曲线上的材料反射光线时，反射光线的强度与入射光线的强度成比例感应下来。

菲涅尔反射定律是定量的，当入射光线的数值为1时，反射光线的数值也会达到一定的值，这个值为I0（即反射光线的最大亮度），我们称之为菲涅尔反射比率。

光的衍射与菲涅尔衍射公式光的衍射是指光通过一个或多个小孔后，产生的波的传播现象。

它是光的波动性质的一种表现，也是研究光的重要原理之一。

菲涅尔衍射公式是用来计算光的衍射现象的数学表达式，它是基于菲涅尔衍射原理和赫兹互衍原理推导得出的。

1. 衍射的基本原理光的衍射是基于光的波动性质，当光通过一个孔或者绕过一个物体时，波的振幅将发生变化，从而导致光的传播方向和强度的变化。

根据衍射的基本原理，可以推导出光的衍射公式。

2. 菲涅尔衍射公式的推导假设光通过一个孔或绕过一个物体后，在衍射屏上形成一系列衍射波阵列，每个波的振幅和相位都会受到影响。

根据菲涅尔衍射原理和赫兹互衍原理，可以得到菲涅尔衍射公式：A = (A1 + A2)e^(ikr)/r其中，A表示在衍射屏上的某一点的光强度（振幅的平方），A1和A2分别表示入射波和散射波的振幅，k是波矢量，r是衍射点到源点的距离。

3. 菲涅尔衍射公式的应用菲涅尔衍射公式可以用于计算不同形状和大小的开孔、物体或间隙对光的衍射效应。

通过将衍射公式应用于实际情况，我们可以计算光的衍射现象，并预测光的传播方向和强度的变化。

4. 衍射的实际应用光的衍射在许多领域都有重要的应用，例如光学显微镜、天文学、图像处理等。

通过掌握和应用衍射原理和衍射公式，人们可以改善光学仪器的性能，提高光学成像的分辨率，并且在物理学和工程学领域有更深入的研究。

5. 总结光的衍射是光的波动性质的一种表现，通过菲涅尔衍射公式可以定量地计算光的衍射效应。

菲涅尔衍射公式基于菲涅尔衍射原理和赫兹互衍原理推导而来，并广泛应用于光学领域的实际问题。

衍射现象的研究和应用有助于改善光学仪器性能，并在科学研究和工程实践中发挥重要作用。

（总字数：241）。

菲涅尔衍射积分推导本文将介绍菲涅尔衍射的概念及其积分推导过程。

在介绍菲涅尔衍射前，我们先来了解一下衍射现象。

衍射是光通过物体边缘或孔径时发生的现象，这种现象会导致光的波前发生变形，使光在远离物体时出现扩散的现象。

菲涅尔衍射是一种特殊的衍射现象，它是由于物体尺寸远大于光波长时发生的衍射现象。

菲涅尔衍射的积分推导过程可以分为以下几个步骤：1. 假设有一平面波在垂直于其传播方向上有一孔径，该孔径大小为d。

我们将孔径上每个点上的光视为发射子波。

2. 对于孔径上任意一点P，其到达某一点M的光波前传播距离为r。

考虑三角形OPM，其中O为光源，由勾股定理可知：r=d+(x-x)+(y-y)，其中(x,y)为光线通过孔径的中心点，(x,y)为点M的坐标。

3. 将上述距离代入菲涅尔衍射公式：U(M)=U∫∫(孔径内所有点)exp(ikr)/r*dxdy，其中U为孔径上一点的振幅，k为波数。

将积分区域限定在孔径d内，即∫∫(孔径内所有点)exp(ikr)/r*dxdy变为∫∫(孔径内所有点)exp(ikd/2r)*exp(ixk(x-x)/r)*exp(ik(y-y)/2r)*dxdy。

4. 对上述积分进行近似处理，忽略分母中的r，将分子分别在x、y方向上进行泰勒展开，保留前两项，即exp(ikd/2r)≈1+ikd/2r和exp(ixk(x-x)/r)≈1+ixk(x-x)/r，exp(ik(y-y)/2r)≈1+ik(y-y)/2r。

5. 将上述近似处理的结果代入积分式中，化简得到U(M)=Uexp(ikr)/r*exp(-ikd/(2r))*exp(ik(x-x)/(2r))*exp(ik(y-y)/(2r))。

6. 将波前因子exp(ik(x-x)/(2r))*exp(ik(y-y)/(2r))代入菲涅尔衍射公式中，得到U(M)=Uexp(ikr)/r*exp(-ikd/(2r))*exp(ik(x-x)/(2r))*exp(ik(y-y)/(2r))*exp(iπλz(1-λx-y)/2z)。

菲涅耳公式推导一、引言菲涅耳公式是描述光在两介质交界面上的光线反射和折射的定律，对理解光的传播和光学现象具有重要意义。

它的推导基于麦克斯韦方程组和边界条件，通过数学方法得到了反射和折射的强度和角度之间的关系。

二、麦克斯韦方程组我们需要了解一些麦克斯韦方程组的基本知识。

麦克斯韦方程组是描述电磁场的基本方程，包括四个方程：电场的高斯定律、磁场的高斯定律、法拉第电磁感应定律和安培环路定律。

这些方程描述了电场和磁场的变化规律和相互作用关系，为推导菲涅耳公式提供了理论基础。

三、边界条件在光在两介质交界面上的反射和折射过程中，有一些边界条件需要满足。

首先，电场和磁场的切向分量在界面上必须连续，即电场和磁场的切向分量在界面上的值相等。

其次，法向分量的电场和磁场的导数在界面上必须连续，即电场和磁场的法向分量在界面上的导数值相等。

这些边界条件保证了光的连续性和一致性。

四、推导过程根据麦克斯韦方程组和边界条件，可以推导出菲涅耳公式。

首先考虑入射光线和界面法线的夹角，利用电场和磁场的边界条件，可以得到反射光的电场和磁场的幅度与入射光的关系。

然后考虑入射光线和界面法线的夹角，利用电场和磁场的边界条件，可以得到折射光的电场和磁场的幅度与入射光的关系。

最后，根据反射和折射的电场和磁场幅度，可以得到反射光和折射光的强度和角度之间的关系，即菲涅耳公式。

五、菲涅耳公式的应用菲涅耳公式在光学中有广泛的应用。

首先，它可以用于计算反射率和透射率，即入射光的一部分被反射，一部分被折射。

这对于设计反射镜、透镜和光学薄膜具有重要意义。

其次，菲涅耳公式可以用于计算反射和折射的角度，根据入射角度和介质折射率的关系，可以确定折射光线的方向。

此外，菲涅耳公式还可以用于研究偏振光的反射和折射现象，对于光的偏振性质研究具有重要意义。

六、总结菲涅耳公式是描述光在两介质交界面上的反射和折射现象的定律，通过麦克斯韦方程组和边界条件的推导得到。

它在光学研究中具有重要的理论和实际应用价值，可以用于计算反射率、透射率和光线的角度，对于光学器件设计和光学现象的解释具有重要意义。