菲涅耳公式与薄膜光学

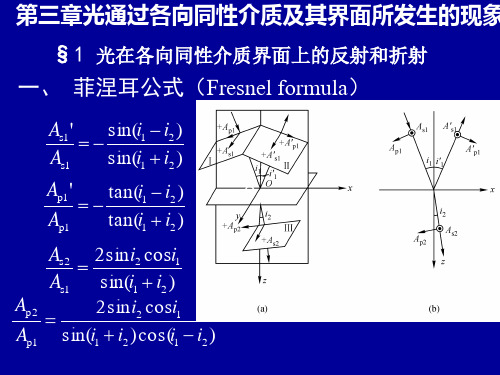
§1-6 菲涅耳公式一．菲涅耳公式电磁波通过不同介质的分界面时会发生反射和折射，在电动力学中将讲到入射、反射和折射三束波在分界面上振幅的大小和方向之间的关系，这一关系可由菲涅耳公式表达出来，上节提到的在反射过程中发生的半波损失问题，就可以用这个公式来解释，这一公式对以后讲到的许多光学现象，都能圆满地加以说明。

菲涅耳公式的内容说明如下：在任何时刻，我们都可以把入射波、反射波和折射波的电矢量分成两个分量，一个平行于入射面，另一个垂直于入射面。

有关各量的平等分量与垂直分量依次用指标P 和S 来表示。

以1i 、'1i 和2i 分别表示入射角、反射角和折射角，它们确定了各波的传播方向（在大多数情况下，只要注意各波的磁场矢量即可，因为知道了各个波的传播方向，各波的磁场矢量就可按右螺旋关系确定）。

以1A 、'1A 和2A 来依次表示入射波、反射波和折射波的电矢量的振幅，它们的分量相应就是1P A 、1'P A 、2P A 和1s A 、1's A 、2s A 。

由于三个波的传播方向各不相同，必须分别规定各分量的某一个方向作为正方向，这种规定当然是任意的。

但是只要在一个问题材的全部讨论过程中始终采取同一种正方向的选择，由此得到的各个关系式就具有普遍的意义，(a)(b)(图1-16)图1-16中xy 平面为两介质的分界面，z 轴为法线方向，xz 平面为入射面，规定电矢量的s 分量以沿着y +方向的为正，这对于入射、反射和折射三个波都相同，图中III II I 、、三个面依次表示入射、反射和折射三个波的波面。

电矢量的P 分量沿着这三个波面与入射面的交线，它们的正方向分别规定为如图1-16)()(b a 、所示，且S 分量、P 分量和传播方向三者构成右螺旋关系。

在传播过程中，电矢量的方向是在不断变化的，我们所注意的仅是在反射、折射过程这一瞬时的变化，所以菲涅耳公式所表示的有关各量的方向都是指紧靠两介质分界面O 点处而言的（在图中为清楚起见，将通过O 点的三个波面画III II I 、、画在离开O 点较远之处）。

菲涅尔方程式
菲涅耳方程式（Fresnel Equations）是用来描述光在两种介质界面上反射和透射的现象和规律的方程式。

它由奥古斯汀·菲涅耳（Augustin-Jean Fresnel）在19世纪提出，并成为光学领域中的重要理论工具。

菲涅耳方程式分为反射方程和透射方程，分别描述了光在界面上的反射和折射（透射）行为。

这些方程式基于电磁波的传播和边界条件，可以通过麦克斯韦方程和边界条件进行推导。

反射方程描述了入射光波在介质界面上的反射行为。

对于垂直入射的光，反射系数（反射光强与入射光强之比）可以通过下述菲涅耳反射方程计算：
r = (n1 - n2) / (n1 + n2)
其中，n1和n2分别是两种介质的折射率，r是反射系数。

透射方程描述了入射光波通过介质界面的折射行为。

同样对于垂直入射的光，透射系数（透射光强与入射光强之比）可以通过下述菲涅耳透射方程计算：
t = 2n1 / (n1 + n2)
其中，n1和n2分别是两种介质的折射率，t是透射系数。

需要注意的是，菲涅耳方程式仅适用于垂直入射的光，并且忽略了光在界面上的散射和吸收行为。

在实际应用中，还需要考虑光的入射角度、极化状态和表面特性等因素，并结合其他衍射、干涉等现象来对界面上的光行为进行更全面的描述。

菲涅耳方程式在材料科学、光学器件设计和表面反射控制等领域中具有广泛的应用，并能解释和预测光在界面上的反射和透射现象。

菲涅尔公式是描述光在两种介质交界面上反射和折射现象的一组公式，由法国物理学家菲涅尔在19世纪提出。

该公式包含了入射光线的角度、两种介质的折射率以及反射和折射光线的角度等因素。

菲涅尔公式可以用来计算反射和透射光线的强度和相对方向，是光学研究中非常重要的工具。

它的表达式形式较为复杂，包括两个方程式：一个是描述垂直入射光线的情况，另一个是描述斜入射光线的情况。

具体表达式如下：
垂直入射光线：
反射系数R = ((n1-n2)/(n1+n2))²
透射系数T = 1-R
斜入射光线：
反射系数R = ((n1cosθ1 - n2cosθ2)/(n1cosθ1 + n2cosθ2))²
透射系数T = 1-R
其中，n1和n2表示两种介质的折射率，θ1和θ2表示入射光线和反射/折射光线的夹角（取决于光线从哪种介质入射），cos表示夹角的余弦值。

- 1 -。

光在介质膜界面的反射率一、光垂直入射介质界面时的反射率光在介质界面反射、折射时的菲涅耳公式为:式中r s 、r p 分别为s分量、p分量振幅反射系数, t s 、t p 分别为s分量、p分量振幅透射系数.二、单层膜的反射率首先计算单层膜反射率的多光束干涉形式. 也就是说, 上述计算单层薄膜反射率的双光束干涉形式仅是近似的处理方法.如图, 假定在折射率为n 2 的光学基板上有一层厚度均匀的薄膜, 膜折射率为n 1 , 膜的几何厚度为d 1 , 入射介质的折射率为n 0 , 当光束照射到薄膜上表面时, 光束在薄膜两表面上要多次反射, 因而产生一组反射光束1, 2, 3,……, 和一组透射1’,2’,3’,……，如果入射光的振幅为E 0 , 则各反射光束的振幅为这里的分别表示在两个界面上的反射系数和透射系数(图2).由斯托克斯定律可知, .式(1)中的为膜的位相厚度,即两相邻光束间的位相差为.反射光的合振幅E R 为于是我们得到单层膜的反射系数为从上式可见, 单层膜的反射系数是一个复数,故上式可写成上式中可通过菲涅尔公式求得为膜的位相厚度. 为反射光相移,表示反射光波的位相落后于入射光波的值.单层膜的反射率R 为从上面的结果我们可以看出,单层膜的两个界面可以用一个等效界面来代替.如图3所示,膜的折射率为nk,入射介质的折射率为nk-1,出射介质(或基板玻璃)的折射率为nk+1,膜的位相厚度是k,设单层膜上界面的反射系数为rk,下界面的反射系数为rk+1,于是这个单层膜的等效界面的反射系数为,综上求得:三、多层膜的反射率经过这样处理和理解以后, 我们可以将单层膜的反射率计算推广应用到多层膜场合. 首先从与基片相邻的底层膜开始, 将底层膜的两个界面等效成一个界面, 然后再将这个等效界面与上一个界面等效为一个界面, 依次往上递推到膜系的顶层的第一个界面, 如图由之前的结果可知：根据折射定律, 有因此可以得到各层膜中光的入射和折射角i对各层膜有，根据菲涅尔公式计算出各层的菲涅尔系数，对p分量，对s分量最后求出反射率四、增透膜，增反膜为了减少光在光学元件表面上的反射损失,可利用薄膜上、下表面反射光的相消干涉来减少反射光. 因此常在光学元件的表面镀制介质薄膜———增透膜.为了提高反射率, 常在玻璃上镀制增反膜, 增反膜的折射率比玻璃的高, 称为高膜。

实验名称 菲涅尔公式的认识一、实验目的:加深理解菲涅尔公式，对给出的反射波或折射波与入射波振幅的相对变化进行分析，以及对相位变化进行分析。

二、实验原理:任一方位振动的光矢量E 都可以分解成互相垂直的两个分量称平行于入射面振动的分量为光矢量的p 分量，记为EP 。

称垂直于入射面振动的分量为光矢量的s 分量，记为ES 。

1.菲涅耳公式:表示反射波、折射波与入射波的振幅和位相关系。

（1）S 波（垂直于入射面分量）的菲涅耳公式s r ——S 波的振幅反射系数 s t ——S 波的振幅透射系数（2）P 波（平行于入射面分量）的菲涅耳公式p r ——P 波的振幅反射系数 p t ——P 波的振幅透射系数2.光从光疏介质入射到光密介质（如空气射向玻璃）当 时，即垂直入射时， 都不为零，表示存在反射波和折射波。

当 时，即掠入射时， 即没有折射光波。

s t 、p t 随1θ的增大而减小；s r 随1θ的增大而增大，直到等于1；221122112121s 1s 1s n n n n A A r θθθθθθθθcos cos cos cos )sin()sin('+-=+--==2211112121s 1s 2s n n n 22A A t θθθθθθθcos cos cos )sin(sin cos +=+==211221122121p 1p1p n n n n tg tg A A r θθθθθθθθcos cos cos cos )()('+-=+-==211211212112p1p 2p n n n 22A A t θθθθθθθθθcos cos cos )cos()sin(cos sin +=-+==p s p s t t r r 、、、01=θ901=θ0t t 1r r p s p s ====,p r 值在() 902B B 1=+=θθθθ时，有0r p =，即反射光波中没有p 波，只有s 波，产生全偏振现象。

二、证明：1.光学厚度为入M2的膜层，在其中心波长处为虚设层。

2.证明：在边界处E与H的切向分量连续。

3.试证明所谓的薄膜系统的不变性：即当薄膜系统的所有折射率都乘以一个相同的常数，或用它们的倒数替代时，膜系的反射率和透过率没有任何变化。

三、设计问题：1.分析并设计一个应用于太阳能集热器的膜系，注意阳光的色温为5800K,黑体辐射为750Ko（查找资料获得阳光辐射曲线和照体辐射曲线，利用TFCalc设计膜系）。

2.计算一个简单周期规整膜系A|（LH）6 7 8|S的截止波长位置、带宽、截止深度及其在截止波长处的反射率（H:T6 n=2.3； L:SiO2, n=1.45； A:空气，S:K9）。

3.设计一款宽带高反射膜，H:T I O2, n=2.3： L:S I O2, n=1.45,需要考虑那些主要问题？4.设计一个覆盖可见光波段的宽带全介质高反射膜，叙述其设计思想与设计步骤。

5.设计一个可见光区的减反射膜，要求如下：波长区间400〜700nm,平均反射率＜0.4%,最人反射率＜0.6%。

10•请设计棱镜分色系统所需要的所有膜系6 设计一个可见光区的高反射膜，要求如下：波长区间400〜700nm,平均反射率＞99%,最小反射率＞98%。

7 在空气中自然光入射到金属材料铝和银时，用TFCale软件分析两种材料反射光偏振效应最大值出现的角度与数值的步骤。

（入=500nm, Al： 0.64-/5.50, Ag： 0.050-/2.87）8 请设计CCD使用的IR-CUT膜系9.请设计冷光镜11.设计投影机用X棱镜中的两个膜系12.设计泰曼干涉仪的金属（A1）分光镜（光源为He-Ne激光），要求到达接收平面的干涉图对比度最好。

13.试在玻璃基底（n=1.52）上设计一诱导透射滤光片，中心波长为500nin,要求峰值透过率大于70%,在400mii〜1500nm的波长范围内背景透过率小于0.1%,整个多层膜与合适的吸收玻璃胶合。

菲涅尔方程式
摘要：
1.菲涅尔方程式简介
2.菲涅尔方程式推导过程
3.菲涅尔方程式在物理中的应用
4.菲涅尔方程式的重要性和意义
正文：
菲涅尔方程式是描述光在物质中传播的一个基本方程。

它描述了光在物质中的吸收和散射现象，是研究光学现象的重要工具。

菲涅尔方程式可以推导出来。

首先，我们需要知道物质的线性吸收系数α和散射系数σ。

然后，我们可以得到物质的复折射率n，它由n = 1 + (k - 1)/2 * (α + iσ)^2求得。

其中k是物质的阶数，对于第一阶物质，k = 2。

最后，我们可以得到菲涅尔方程式：P = (1 - R) * I = (1 - e^(-2 * α * L)) * I，其中P是透射光强，R是反射光强，I是入射光强，L是光在物质中的传播距离，e是自然对数的底数。

菲涅尔方程式在物理中有广泛的应用。

例如，它可以用来解释光在空气和玻璃中的传播，也可以用来研究光在生物组织中的传播。

通过菲涅尔方程式，我们可以了解光的吸收和散射对光传播的影响，从而更好地理解和利用光。

菲涅尔方程式在光学研究中具有重要意义。

它提供了一个理论框架，可以帮助我们理解光在物质中的传播规律。

同时，菲涅尔方程式也为光学技术的应用提供了理论支持，如光学通信、光学成像和光学传感等。