3.5 有电介质时的高斯定理
- 格式:docx
- 大小:40.67 KB
- 文档页数:2

有介质时的高斯定理,写出其物理意义
高斯定理(也称为高斯通量定理)是电磁学中的一个基本定理,描述了电场或磁场通过一个封闭曲面的总通量与在该曲面内部源的大小之间的关系。
具体表达式为:对一个任意形状的封闭曲面,电场或磁场通过该曲面的总通量等于该曲面内部电荷或磁荷的代数和。
物理意义如下:
1. 电场或磁场通过一个封闭曲面的总通量是该曲面内部电荷或磁荷的性质之一,可以帮助我们了解场的发源和分布。
例如,通过测量通过一个闭合曲面的电场通量,可以推断该闭合曲面内部的电荷分布情况。
2. 高斯定理对于计算电场或磁场的分布以及场源的性质具有重要的应用。
通过选取适当的曲面以及利用高斯定理,可以简化计算复杂电场或磁场的过程,提高计算效率。
3. 高斯定理还有与能量和电荷守恒定律的联系。
当封闭曲面内部不存在电荷时,即电荷守恒定律成立时,通过该曲面的电场通量为零。
这可以用来推导电场能量的守恒。
总的来说,高斯定理在电磁学中具有重要的作用,它可以帮助我们理解场的分布、推断电荷或磁荷的性质,并且简化电场或磁场计算的过程。




有电介质时的高斯定理
有电介质时的高斯定理是电学中的一个重要定理,它描述了电场的分布与电荷分布的关系。
此定理的公式表述为:电场穿过一个封闭曲面的通量等于该曲面内部的电荷总量的比例,即ΦE=Q/ε0,其中ΦE为电场的通量,Q为曲面内部的电荷总量,ε0为真空中的电介质常数。
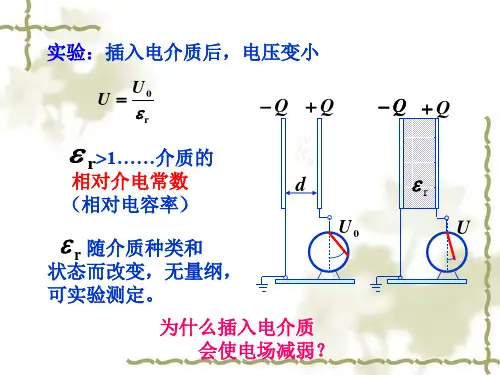
在有电介质时,电场的分布受到电介质的影响。
电介质的存在会使电场强度发生改变,这是因为电介质的分子会被电场极化,从而产生极化电荷。
这些极化电荷会改变电场的分布,使电场在电介质中的强度比在真空中的强度小。
因此,在有电介质时,要考虑电介质对电场的影响,才能准确地计算电荷的分布。
在应用高斯定理时,通常需要选择一个适当的曲面来计算电场的通量。
曲面的选择应当考虑到电荷分布的对称性,以便简化计算。
在有电介质时,曲面的选择也需要考虑到电介质的影响。
如果曲面穿过电介质,那么在计算电荷总量时,需要将电介质中的极化电荷也计算在内。
高斯定理的应用范围很广,包括电场的计算、电容器的设计、电荷分布的测量等。
在电场的计算中,高斯定理可以用来求解各种电场分布,例如电偶极子、均匀带电球面等。
在电容器的设计中,高斯定理可以用来计算电容器的电容量,从而确定电容器的电荷储存能
力。
在电荷分布的测量中,高斯定理可以用来测量电荷的总量,从而确定电荷的分布情况。
有电介质时的高斯定理是电学中的一个重要定理,它描述了电场的分布与电荷分布的关系。
在应用该定理时,需要考虑到电介质的影响,并选择适当的曲面来计算电场的通量。
高斯定理的应用范围很广,包括电场的计算、电容器的设计、电荷分布的测量等。

3.5有电介质时的高斯定理
3.5 有电介质时的高斯定理
3.5.1电介质中的场强
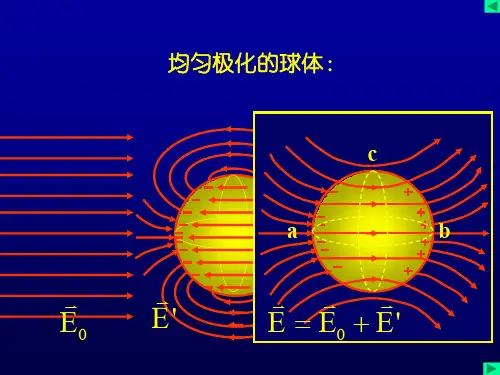
电介质放入外电场中产生极化,电介质中的电场是极化电荷产生的附加电场E ’和外电场E 0的矢量和。
即:E = E 0+ E ’。
电介质中的电场不为零,但显著地被削弱了。
3.5.2电位移,有电介质时的高斯定理
真空中产生电场的电荷是自由电荷。
有介质存在时,电介质的内部或表面上出现极化电荷,极化电荷也要激发电场。
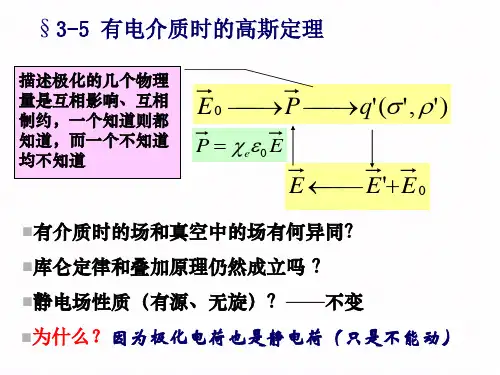
可见,有介质存在时,增加了新的场源电荷即极化电荷。
但是,新的场源只改变原有静电场的大小,不改变静电场的性质。
即对有介质存在时的静电场,高斯定理和环路定理仍然成立。
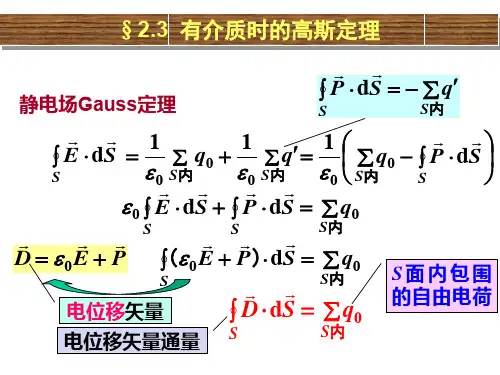
1、有电介质时的高斯定理
通过前面分析,此时高斯定理应写为:
()001S d q q ε'?=+?? E S
其中q 0和q ’分别为闭合面S 所围区域内的自由点和极化电荷。
而
S
q d '=- P S 00
1S S d q d ε???=- E S P S ()0
0S d q ε+?=?? E P S 引入一个辅助性的矢量(称为电位移)
0ε=+D E P
则上式可改写为
0S d q ?=??
D S 上式叫做有电介质存在时的高斯定理。
对于各向同性电介质有
0εχ=P E
()01εχ=+D E
上式说明电介质中任一点的D 与该点的E 方向同向,大小成正比。
电介质的介电常量:
()01εεχ=+ 电介质的相对介电常量:
01r εεχε==+ 0r εεε==D E E
例1【P103】、例2【P104】。

第18讲有电介质时的高斯定理电极化强度 电位移矢量 的高斯定理 DE E E '+= 00E + ++ - - - σ ' 原外电场 σ ' 的电场E ' V p P i i ∆∑= lim ∑=⎰⋅int0d q S D S PE D+=0ε与 的关系 静电场中的各向同性、线性电介质的高斯定理 与 的关系 int 0q D E Pσ'q 'E 与 的关系 与的关系 当自由电荷 q 0int和电介质分布具一定对称性时,应用 高斯定理 便于解决问题。
DEDD P Pσ'σ'q '∑⎰=⋅int 0d q S D S E E D εεε==r 0n ˆeP ⋅=' σ⎰'='S q d σE P )(1r 0-=εε[Q5.18.1] 一无限大各向同性均匀电介质平板,厚度为 d ,相对介电常数为 εr ,内部均匀分布有电荷体密度为 ρ0 的自由电荷。
求:介质板内、外的 、 、 。
drε0ρEPD解: 带电体有面对称,故 、 、 垂直于平板。
dX0S x = 0 = 2DS 0 00022S x DS ρ=xD 0ρ=d S DS 0002ρ=dD 20ρ=r ε0ρ⎰⋅+⎰⋅=⎰⋅两底侧S D S D S D S d d d 2d x ≤, 2d x ≥, , ,∑=⎰⋅int0d q S D SD E P S 0 S ' S 0'r 0εεDE =r00εερx =均匀场 = 0xD 0ρ=dD 20ρ=dX0xr ε0ρEP )(1r 0-=εεερεxP 0r 1)(-=E P )(1r 0-=εεr2d x ≤, 2d x ≥, 0εD E =002ερd =[Q5.18.2]平行板电容器极板面积为S,间距为d,中间有两层厚度各为d1和d2 (d1+d2=d)、相对介电常数分别为εr1和εr2的电介质层。
有介质时的高斯定理公式有介质时的高斯定理公式是物理学中的基本定理之一,它描述了电场、重力场等物理场在有介质的情况下的分布规律。
本文将介绍有介质时的高斯定理公式及其应用。
高斯定理公式指出,电场的通量与电荷量成正比,与介质极化强度成反比。
在有介质的情况下,电荷会在介质中引起电极化,从而影响电场的分布。
因此,高斯定理公式在描述有介质中电场分布时变得更加复杂。
在有介质时,高斯定理公式可以表示为:$$ \oint_S \mathbf{E} \cdot d\mathbf{S} = \frac{1}{\epsilon_0}\int_V \rho dV - \oint_S \mathbf{P} \cdot d\mathbf{S} $$其中,S是一个封闭曲面,V是该曲面所围成的空间区域,$\mathbf{E}$表示电场强度,$\rho$表示电荷密度,$\mathbf{P}$表示介质的极化强度,$\epsilon_0$为真空介电常数。
公式右边第一项表示电荷在该区域内总共产生的电场通量,第二项表示介质极化所产生的电场通量。
公式左边的积分表示电场穿过曲面S的总通量。
在应用高斯定理公式时,需要注意几个关键点。
首先,曲面S需要是一个封闭曲面,而不是一个任意的曲面。
其次,积分中包含的介质极化强度需要根据具体情况进行计算。
最后,公式只适用于稳态电场的情况,不适用于变化的电场。
高斯定理公式在物理学中有着广泛的应用,特别是在电学、磁学、地球物理学等领域。
在电学中,高斯定理公式可以用于计算电容器的电容量;在磁学中,可以用于计算磁通量;在地球物理学中,可以用于计算地球重力场分布。
有介质时的高斯定理公式是物理学中一个非常基础和重要的定理,描述了物理场在有介质时的分布规律。
在实际应用中,需要注意公式的条件和具体计算方法,才能得到准确的结果。
3.5 有电介质时的高斯定理
3.5.1电介质中的场强
电介质放入外电场中产生极化,电介质中的电场是极化电荷产生的附加电场E ’和外电场E 0的矢量和。
即:E = E 0+ E ’。
电介质中的电场不为零,但显著地被削弱了。
3.5.2电位移,有电介质时的高斯定理
真空中产生电场的电荷是自由电荷。
有介质存在时,电介质的内部或表面上出现极化电荷,极化电荷也要激发电场。
可见,有介质存在时,增加了新的场源电荷即极化电荷。
但是,新的场源只改变原有静电场的大小,不改变静电场的性质。
即对有介质存在时的静电场,高斯定理和环路定理仍然成立。
1、有电介质时的高斯定理
通过前面分析,此时高斯定理应写为:
()001S d q q ε'⋅=+⎰⎰ E S
其中q 0和q ’分别为闭合面S 所围区域内的自由点和极化电荷。
而
S
q d '=-⋅⎰⎰ P S 00
1S S d q d ε⎡⎤⋅=-⋅⎣⎦⎰⎰⎰⎰ E S P S ()0
0S d q ε+⋅=⎰⎰ E P S 引入一个辅助性的矢量(称为电位移)
0ε=+D E P
则上式可改写为
0S d q ⋅=⎰⎰
D S 上式叫做有电介质存在时的高斯定理。
对于各向同性电介质有
0εχ=P E
()01εχ=+D E
上式说明电介质中任一点的D 与该点的E 方向同向,大小成正比。
电介质的介电常量:
()01εεχ=+ 电介质的相对介电常量:
01r εεχε==+ 0r εεε==D E E
例1【P103】、例2【P104】。