有电介质的高斯定理
- 格式:ppt
- 大小:1.92 MB
- 文档页数:48







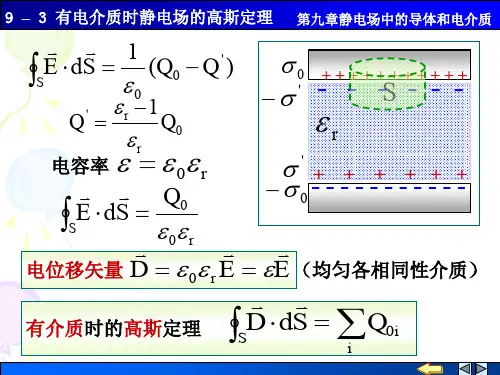
有电介质时的高斯定理
有电介质时的高斯定理是电学中的一个重要定理,它描述了电场的分布与电荷分布的关系。
此定理的公式表述为:电场穿过一个封闭曲面的通量等于该曲面内部的电荷总量的比例,即ΦE=Q/ε0,其中ΦE为电场的通量,Q为曲面内部的电荷总量,ε0为真空中的电介质常数。
在有电介质时,电场的分布受到电介质的影响。
电介质的存在会使电场强度发生改变,这是因为电介质的分子会被电场极化,从而产生极化电荷。
这些极化电荷会改变电场的分布,使电场在电介质中的强度比在真空中的强度小。
因此,在有电介质时,要考虑电介质对电场的影响,才能准确地计算电荷的分布。
在应用高斯定理时,通常需要选择一个适当的曲面来计算电场的通量。
曲面的选择应当考虑到电荷分布的对称性,以便简化计算。
在有电介质时,曲面的选择也需要考虑到电介质的影响。
如果曲面穿过电介质,那么在计算电荷总量时,需要将电介质中的极化电荷也计算在内。
高斯定理的应用范围很广,包括电场的计算、电容器的设计、电荷分布的测量等。
在电场的计算中,高斯定理可以用来求解各种电场分布,例如电偶极子、均匀带电球面等。
在电容器的设计中,高斯定理可以用来计算电容器的电容量,从而确定电容器的电荷储存能
力。
在电荷分布的测量中,高斯定理可以用来测量电荷的总量,从而确定电荷的分布情况。
有电介质时的高斯定理是电学中的一个重要定理,它描述了电场的分布与电荷分布的关系。
在应用该定理时,需要考虑到电介质的影响,并选择适当的曲面来计算电场的通量。
高斯定理的应用范围很广,包括电场的计算、电容器的设计、电荷分布的测量等。


有电介质的高斯定理好的,那我们就开始聊聊有电介质的高斯定理吧。
电介质的高斯定理啊,听起来就很厉害的样子呢。
其实啊,它就像是一个超级智慧的小管家,管理着电场在电介质中的那些事儿。
你想啊,电场这个东西本来就很神秘,看不见摸不着的,就像一个调皮的小精灵到处乱窜。
但是有了这个高斯定理呢,就好像给这个小精灵套上了一个小缰绳,能让我们更好地去把握它。
在电介质里啊,电荷可不像在真空中那么自由自在了。
电介质会对电场产生影响,就像是给电场设置了一些小障碍一样。
而高斯定理呢,它就像一个聪明的侦探,能透过这些复杂的情况,找到电场和电荷之间的关系。
比如说吧,当有个电介质放在电场里的时候,电介质里的分子会被电场影响,它们会发生极化现象。
这极化就像一群小士兵,被电场这个将军指挥着,重新排列队形。
那高斯定理是怎么做到看透这一切的呢?它通过巧妙地选择一个高斯面,就像在电介质的世界里圈出了一块特殊的领地。
然后呢,根据穿过这个高斯面的电通量,就能知道这个领地里面电荷的情况啦。
这电通量就像是经过这个领地边界的某种流量一样,它能告诉我们很多秘密哦。
你要是把电场想象成水流,那电介质就像是水里的一些小障碍物,会让水流改变方向。
而高斯定理就是那个能算出水流到底是怎么变化的神奇法则。
而且啊,这个定理不仅仅是个干巴巴的公式,它背后有着很多有趣的物理故事呢。
就像每一个科学发现都是人类探索未知的小冒险一样,这个定理的诞生也是科学家们不断思考、不断实验的成果。
理解电介质的高斯定理其实也不是特别难啦,只要你愿意去想象,把那些抽象的东西变成生活中的场景,就像我们刚刚说的小精灵、小士兵、水流这些。
这样的话,这个定理就不再是高高在上、让人望而生畏的东西了,而是像一个可爱的小伙伴,可以跟我们愉快地聊天,告诉我们电介质和电场之间那些有趣的互动呢。
你看,科学有时候就是这么有趣,只要我们换个角度去看,那些看似枯燥的定理也能变得生动起来,就像电介质的高斯定理一样,充满了魅力。