第一讲：数与式

第一讲 数与式基础知识有理数有两种分类方式：有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数 有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数 代数式从确定的数到字母表示数，并且表示数的字母像数一样地参加运算，进而引入代数式，是数学发展史上的一个里程碑，也是我们学习过程的一次飞跃。

代数式使数量关系的表示简洁明了，使具有相同性质的不同数学问题可以用同一个式子表示，是从具体到抽象与概括有有力工具，给研究和计算带来了极大方便。

在列代数式时，就注意以下几点：1、在同一问题中，要注意不同的对象或不同的数量必须用不同的字母表示2、字母与字母相乘可以省略乘号3、在所列代数式中，若有相除关系要写成分数形式4、列代数式是应注意单位，单位名称在代数式后面写出来，如果结果为加减关系，必须用括号将代数式括起来5、代数式中不要使用带分数，带分数与字母相乘是必须把带分数化成假分数。

拓展知识：1、 数集：把一些数放在一起，就组成一个数的集合，简称数集。

（1） 所有有理数组成的数集叫做有理数集；（2） 所有的整数组成的数集叫做整数集。

2、 任何有理数都可以用数轴上的一个点来表示，体现了数形结合的数学思想。

3、 根据绝对值的几何意义知道：|a|≥0，即对任何有理数a ，它的绝对值是非负数。

4、 比较两个有理数大小的方法有：（1） 根据有理数在数轴上对应的点的位置直接比较；（2） 根据规定进行比较：两个正数；正数与零；负数与零；正数与负数；两个负数，体现了分类讨论的数学思想；（3） 做差法：a –b>0 ⇔a>b;（4） 做商法：a/b>1，b>0 ⇔a>b.（做差法与做商法如何进行选择？）数学思想数形结合思想分类讨论的思想整体思想转化的思想一、 妙用定律巧求值例1计算)20031...3121()20041...31211()20031...31211)(20041...3121(+++⨯++++-+++++++例2求1002-992+982-972+…+42-32+22-12例3 计算 1+5+52+53+…+599+5100的值．二、 比较数的大小例4比较a1与a ，3a 与2a 的大小关系例5设a 1,a 2,a 3,…a 2000都是有理数，令)...)(...(),...)(...(199932200021200032199921a a a a a a N a a a a a a M ++++++=++++++=，试比较M 、N 的大小。

第一讲 数与式第1课时 实数的有关概念考点一、实数的概念及分类 〔3分〕正有理数有理数 零 有限小数和无限循环小数 实数 负有理数 正无理数无理数 无限不循环小数〔π〕、开方开不尽的数 负无理数凡能写成)0p q ,p (p q≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；考点二、实数的倒数、相反数和绝对值 〔3分〕2、数轴：数轴是规定了原点、正方向、单位长度的一条直线.3、相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0； (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4、绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 绝对值的问题经常分类讨论；5、倒数假设ab =1⇔ a 、b 互为倒数；假设ab =-1⇔a 、b 互为负倒数。

倒数等于本身的数是1和-1。

零没有倒数。

11a a-=考点三、平方根、算数平方根和立方根 〔3—10分〕 6、平方根①如果一个数的平方等于a ，那么这个数就叫做a 的平方根〔或二次方跟〕。

一个数有两个平方根，他们互为相反数；零的平方根是零；负数没有平方根。

正数a 的平方根记做“a ±〞。

②算术平方根正数a 的正的平方根叫做a 的算术平方根，记作“a 〞。

正数和零的算术平方根都只有一个，零的算术平a ，2a =；注意a 的双重非负性：0≥a a ≥07、立方根如果一个数的立方等于a ，那么这个数就叫做a 的立方根〔或a 的三次方根〕。

一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

第一讲 数与式§1.1 实数知识梳理一、基本概念1.规定了_______、_______、______的直线叫做数轴,数轴上的点与实数是一一对应关系.2.只有_______的两个数叫做互为相反数，零的相反数是零．3._______的两个有理数互为倒数.4.一个数a 的绝对值是在数轴上表示数a 的点与原点的距离，数a 的绝对值记做a ．5. 把一个数记成na 10⨯±的形式，其中,n a ，101<≤是_____，这种记数法叫做科学记数法． 6.一个近似数四舍五入到哪一位，就说它精确到哪一位，这时，从左边第一个不是零的数字起到右边精确的数位止的所有数字，都叫做这个数的________.7.无理数是_____________,______和______统称为实数,实数与数轴上的点是一一对应的. 8.式子)0(≥a a 叫做二次根式，)0(≥a a 是一个非负数. 二、重要结论1.如果a 与b 互为相反数，则有a+b=0;如果a 与b 互为倒数，则有ab=1.2._______的绝对值是它本身，_____的绝对值是它的相反数．3.两个负数比较,______大的反而小;数轴上右边的点所表示的数_________左边的点所表示的数.()()()200a a a a a a≥⎧⎪=⎨-⎪⎩=_____(a ≥0).5.0a =_____(a ≠0), na -=__________( a ≠0,n 是正整数).考点呈现考点1 实数的有关概念例1（2012年凉山州）若x 是2的相反数，|y|=3，则x-y 的值是（ ） A ．-5 B ．1 C ．-1或5 D ．1或-5解析：因为2的相反数是-2，所以x=-2；因为3和-3的绝对值都是3，所以y=±3. 分两种情况分别计算.当x=-2，y=3时，x-y=-5；当x=-2，y=-3时，x-y=1.故选D.点评:只有符号不同的两个数叫做互为相反数，互为相反数的两个数绝对值相等.正数的绝对值是它本身，负数的绝对值是它的相反数,0的绝对值是0.例2（2012年安顺市）在实数：3.14 159 1.010 010 001, 12.4 ，π，227中，无理数有（ ） A ．1个 B ．2个 C ．3个 D ．4个解析：因为3.14159，1.010010001是有限小数，所以是有理数. 12.4 是无限循环小数，所以不是无理数，4643=是有理数，722是分数，是有理数，只有π是无限不循环小数，所以是无理数的就1个，故选A.点评：目前我们所学的无理数可分为三类：①开方开不尽的数,如②化简后含π的数,如:2π；③特定结构的数,如:1.202 002 000 2…(每两个2之间依次多一个0).考点2 科学记数法与有效数字例3 （2012年贵州铜仁）从权威部门获悉，中国海洋面积是299．7万平方公里，约为陆地面积的三分之一， 299．7万平方公里用科学记数法（保留两位有效数字）表示为（ ） A ．6103⨯平方公里 B ．7103.0⨯平方公里 C ．6100.3⨯平方公里D ．61099.2⨯平方公里解析：299.7万=2.997×106，保留两个有效数字为6100.3⨯.故选C ．点评:把一个数写成a ×10n 的形式，其方法是①确定a （a 是整数数位只有一位的数）；②确定n ，当原数的绝对值≥10时，n 为正整数，n 等于原数的整数位数减1；当原数的绝对值＜1时，n 为负整数，n 的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．考点3 实数与数轴例4（2012年聊城市）在如图1所示的数轴上，点B 与点C 关于点A 对称，A 、B 两点对应的实数分别是3和－1，则点C 所对应的实数是（ ）A.1+3B. 2 +3C. 23－1D. 23+1解析：因为AB=13+,所以AC=13+.因为A 对应的是3，所以C 对应的是132+.故选D ． 点评:处理这类问题的关键是正确把握对称点的特征,找出其中的等量关系,再进行实数的运算. 考点4 实数的估算例5（20121的值在（ ）A ．2到3之间 B.3到4之间 C ．4到5之间 D ．5到6之间解析：因为,964<<所以,362<<所以314<<.故选B ．点评:实数的估算一般步骤是首先将原数平方，看其在哪两个平方数之间，运用这种方法可以估计一个带根号的数的整数部分,从而估计其大致范围.例6（2012年张家界）实数a 、b 在轴上的位置如图2所示，且b a >，则化简b a a +-2的结果为（ ）A ．b a +2 B.b a +-2 C .b D.b a -2解析：由题设可知，a <0，a +b<0，所以b a a +-2=()[]a a b a a b a a b b -+=---+=-++=，故选C.点评:根据绝对值的意义去掉绝对值符号是解题关键. 考点5 非负数的性质例7（2012年广东省改编）若x 、y 为实数，且满足|x －，则2012()xy的值是.图 2解析：因为03|3|=++-y x ，所以03,03=+=-y x .所以3,3-==y x . 所以1)1()(20122012=-=yx ．故填-1．点评:两个或多个非负数之和等于0，则每个非负数都等于0，从而可以求得各字母的值，进而求得代数式的值．考点6 实数的运算例8 (2012年绵阳市）计算：()2-πo -28-3+⨯⎪⎭⎫⎝⎛82-. 解析:原式=1-22-+×（-22） =1-（2-2）×（-22）=1+2-1=2. 点评：实数的运算，在解题时要注意运算顺序和公式的综合应用．例9 (2012年衡阳市)= ． 解析： 原式=6662=-.点评:二次根式相乘，把被开方数相乘，作为积的被开方数；合并同类二次根式时，只把系数相加减，被开方数不变．误区点拨1. 运算错误 例1 计算:15÷15×(-5). 错解:原式=15÷(-1)=-15.剖析:乘除法是同级运算，应按从左到右的运算顺序依次进行计算. 正解: 原式=15×5×(-5)=-375.例2 计算:12÷(14-13). 错解:原式=12÷14-12÷13=12×4-12×3=12.剖析:错解把乘法的分配律机械地类比到除法的运算中,造成错误. 正解: 原式=12÷(-112)=12×(-12)=-144. 例3 计算:()23-=_______.错解:-3.剖析:产生错误的原因是误认为a a =2.本题中，()23-表示()23-的算术平方根,而()23-=9，所以()23-的算术平方根就是9的算术平方根,即()23-=3.正解:3.2. 考虑不周,造成漏解例4 已知3a-22与2a-3都是实数m 的平方根,求m 的值.错解:由题意,得3a-22+2a-3=0,解得a=5.所以m=().49722322==-a剖析:此题应分两种情况:一种是3a-22与2a-3相等，另一种是3a-22与2a-3互为相反数.正解:(1)当3a-22与2a-3互为相反数,即3a-22+2a-3=0时,解得a=5.所以m=()49722322==-a ;(2)当3a-22与2a-3相等,即3a-22=2a-3时,解得a=19.所以m=()12253522322==-a .3.忽视隐含条件例5 2的结果为（ ）Ａ．5x - Ｂ．25x - Ｃ．xＤ．x -错解：原式=()()12312---x x =(1-3x)-(2x-1)=2-5x.故选Ｂ．剖析：本题错在忽视了二次根式成立的隐含条件．题目中12-x 有意义，说明隐含了条件210x -≥，即12x ≥，可知310x -≥． 正解：由12-x 知210x -≥，得12x ≥，从而有310x -≥，所以原式=()()12312---x x =|1-3x|-(2x-1)=(3x-1)-2x+1=x.故选C ．技法指导1.实数部分其解答的要求是“简单、直接”.所谓“简单”就是题目的结构简单、要求少、计算量和思维量均小、没有技巧和思维层面的要求；所谓“直接”就是题目涉及的知识点少、一目了然.2.这部分复习,准确把握概念是关键,练习应该精而少.跟踪训练1.下列说法正确的是( )A.0)2(π是无理数B.33是有理数 C.4是无理数D.38-是有理数2.（2012年达州市）今年我市参加中考的学生人数约为41001.6⨯人．对于这个近似数，下列说法正确的是（ ）A.精确到百分位，有3个有效数字B.精确到百位，有3个有效数字C.精确到十位，有4个有效数字D.精确到个位，有5个有效数字 3.（2012年南京市）下列四个数中，是负数的是（ ） A ．2- B. 2)2(- C.2-D.2)2(-4.（2012年宁波市）已知实数x ，y 2(1)0y +=，则x －y 等于（ ） A ．3 B ．－3 C ． 1 D ． －15.（2012年菏泽市）已知21x y =⎧⎨=⎩是二元一次方程组81mx ny nx my +=⎧⎨-=⎩的解，则2m －n 的算术平方根为（ ）A ．±2B ．． 2 D ． 46.（2012年湘潭市）文文设计了一个关于实数运算的程序，按此程序，输入一个数后，输出的数比输入的数的平方小1，若输入7，则输出的结果为（ ）A. 5B. 6C. 7D. 87.实数a化简后为( ) A ． 7 B ． －7 C ． 2a －15 D ． 无法确定8.对于任意不相等的两个实数a 、b ，定义运算※如下：a ※b =b a b a -+，如3※=8※12= ．9.若将三个数11,7,3-表示在数轴上，其中能被如图所示的墨迹覆盖的数是__________________．10.计算：|－5|－3)0+6×(1132-)+(－1)2.§1.2 代数式、整式、分式知识梳理一、基本概念1.所含字母______，并且相同字母的____也分别相同的项叫做同类项．几个常数项也是同类项．把多项式中的同类项合并成一项，叫做_______．2. 因式分解就是把一个多项式表示为几个____的形式，因式分解与_______是互逆的,分解因式必须进行到每一个多项式都不能再分解为止.3.分母中含有______的代数式叫分式,分式有意义的条件为______,分式值为零的条件为________.______和______统称有理式. 二、重要结论 1.幂的运算性质:m n a a ⋅=_____,()____nm a =,()nab =_______,m n a a ÷=_____(0≠a )n m ,为整数.2.乘法公式: ()()a b a b +-=_______；完全平方公式：2()a b ±=___________.3.因式分解的一般方法有_______和_______.其中公式法涉及到的公式有22a b -=________;222a ab b ±+=________.4.分式的基本性质用字母表示为______________.5.分式的加减法则表示为a b c c ±=______，b ca d±=______;5 a 0 10分式的乘除法则表示为a cb d ⨯=______,a cb d÷=_______. 考点呈现考点1 相关概念例1（2012年上海市）在下列代数式中，次数为3的单项式是( )A . xy 2B . x 3－y 3C .x 3y D .3xy解析: 由题目可知结果受两个条件制约，首先这个式子必须是单项式，其次这个单项式的次数为3． 由单项式次数的概念，可知次数为3的单项式是xy 2 ，所以选A .点评:要正确理解单项式的次数. 例2（2012年雅安市）如果单项式-221y x a 与by x 331是同类项，那么a,b 的值分别为 （ ） A.2，2 B.-3， 2 C.2，3 D.3，2 解析：因为单项式-221y x a 与by x 331是同类项，所以a=3, b=2. 故选D. 点评:同类项的识别关键是抓好“两相同”：一是字母相同，二是相同字母的指数也相同.考点2 因式分解例3（2012年宜宾市）分解因式：=+-22363n mn m _______.解析：先提公因式，再利用完全平方公式.原式=3（m 2－2mn ＋n 2）＝3（m －n ）2.点评:因式分解一定注意先后顺序：有公因式一定要先提公因式，其次考虑公式法，要注意分解结果是否已经彻底．考点3 代数式有意义及分式值为零的条件 例4（2012年德阳市）使代数式12-x x有意义的x 的取值范围是( ) A ．0≥x B ．21≠x C ．0≥x 且21≠x D ．一切实数 解析：由题意，可得0210x x ≥⎧⎨-≠⎩，解得0≥x 且21≠x .故选C ．点评: 此类题的条件为偶次根式的被开方数是非负数且分式的分母不能等于0． 例5（2012年嘉兴市）若分式12x x -+的值为0，则（ ） A ．2x =-B ．x = 0C ．x = 1或2x =-D ．x = 1解析:由题意，得1020x x -=+≠⎧⎨⎩，解得x=1.故选D ．点评: 分式值为0，则分子等于0，且分母不等于0，.考点4 化简、求值例6（2012年湘潭市）先化简，再求值：11)1111(-÷--+a a a ,其中12-=a .解析：原式＝)1(])1)(1(1)1)(1(1[-∙+-+--+-a a a a a a a ＝)1()1)(1(11-∙-+---a a a a a ＝)1()1)(1(2-∙-+-a a a ＝12+-a . 当12-=a 时，原式＝1122+--＝22-＝2-.点评:对于此类化简求值问题，要先确定运算顺序，再根据分式的乘除运算法则进行计算，最后把相关字母的值代入化简后的结果进行求值即可.误区点拨1. 逆用法则致错例1 已知3,4,m n a a ==则32m na -的值为( )A.2716 B.1627 C. 1627或2716D.不能确定 错解:选D.剖析:错选D 的实质是不会灵活运用幂的运算性质.学习幂的运算性质应注意学会公式的正用、逆用、正逆合用，本题可逆用同底数幂的除法法则以及幂的乘方运算法则求解. 正解: ()()32323232273416m nmnm n aaaaa -=÷=÷=÷=,故选A. 2.混淆因式分解和整式的乘法例2 因式分解:()()223553x y x y +-+.错解:原式=[(3x+5y)+(5x+3y)][(3x+5y)-(5x+3y)]=(8x+8y)(-2x+2y) =-16(x+y)(x-y)=-162x +162y .剖析:上述解法在第四步时,因式分解已经完成,但又用乘法公式把-16(x+y)(x-y)变成-162x +162y ,造成这种错误的原因是混淆了因式分解与整式乘法的意义.正解:原式=[(3x+5y)+(5x+3y)][(3x+5y)-(5x+3y)]=(8x+8y)(-2x+2y) =-16(x+y)(x-y).3.忽视分数线的括号作用例3 计算:21.1x x x -+- 错解:原式=222(1)(1)11111x x x x x x x x -+--+==---.剖析:通分时将-x+1看做一个整体是对的,但添加分数线后,分数线的括号作用不能忽视,应看做是-()11x -.正解: 原式=22(1)2111x x x x x ---=--.技法指导1.代数式、整式和分式的有关概念常以选择题和填空题的形式进行考查，而分式的化简与求值常以解答题的形式进行考查，难度属于中、低档.2.针对这部分内容，建议大家在复习时注意：①知识间的相互联系，如整式乘法与因式分解互为逆变形;进行分式的乘除运算时，约分前需要分解因式;进行分式的加减运算时，通分前也需要分解因式;②约分、通分时切记要保证分式有意义.要特别关注数形结合思想、整体思想、分类讨论思想在分式求值中的应用.跟踪训练 1.多项式1+xy-2xy 的次数及最高项的系数分别是( ) A .2,1 B .2,-1C .3,-1D .5,-12.(2012年宜昌市)若分式21a +有意义，则a 的取值范围是( ) A ．a =0B ．a=1C ．a≠-1D ．a≠03.在下列运算中，计算正确的是（ ） A ．326a a a ⋅=B ．235()a a = C ．824a a a ÷=D ．2224()ab a b =4.（2012年呼和浩特市）下列各因式分解正确的是（ ）A.)2)(2()2(22+-=-+-x x xB.22)1(12-=-+x x xC.22)12(144-=+-x x xD.)2)(2(42-+=-x x x x x5. (2012年宜昌市)根据《国家中长期教育改革和发展规划纲要》，教育经费投入应占当年GDP 的4%．若设2012年GDP 的总值为n 亿元，则2012年教育经费投入可表示为( )A ．4%n 亿元B ．(1+4%)n 亿元C ．(1-4%)n 亿元D ．（4%+n ）亿元 6.（2012年南昌市）已知（m －ｎ）2＝8，（m ＋ｎ）2＝2，则m 2＋ｎ2＝（ ） A ．10 B ．6 C ．5 D ．37.（2012年杭州市）已知m ＝()×(-)，则有( ) A .5＜m ＜6 B . 4＜m ＜5 C .－5＜m ＜－4 D .－6＜m ＜－58.化简：8212-= . 9.（2012年遵义市）化简分式222()1121x x x x x x x x --÷---+，并从-1≤x ≤3中选一个你认为适合的整数x 代入求值.§1.1实数 1.D 2.B 3.C 4.A 5.C 6.B 7.A 8.－29.710.解:|－5|－3)0+6×(1132-)+(－1)2＝5－1+(2－3)+1＝4．§1.2代数式、整式、分式 1.C 2.C 3.D 4.C 5.A 6.C 7.A8.-29.解：原式＝22221()11x x x x x x x x-+-⋅--- ＝22(1)(1)1(1)(1)(1)(1)x x x x x x x x x x x --⋅-⋅--+--＝111x -+＝1x x +. ∵不能取-1，0，1 ∴当x ＝2时，原式＝22213=+.。

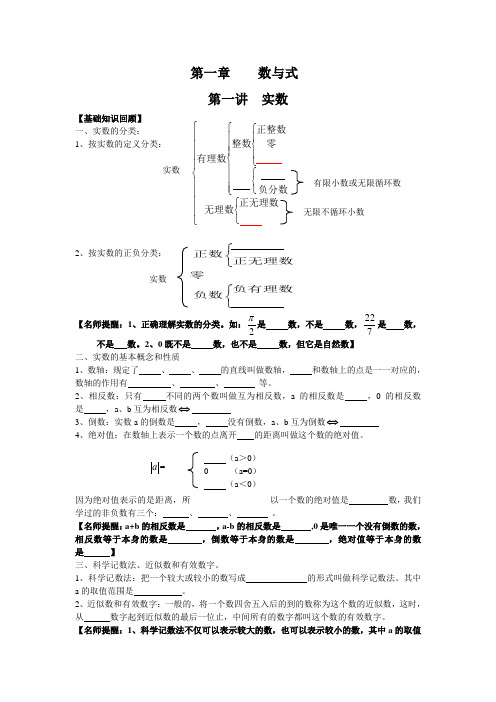
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类： 1、按实数的定义分类： 实数 有限小数或无限循环数2、按实数的正负分类：实数【名师提醒：1、正确理解实数的分类。

如：2π是 数，不是 数，722是 数，不是 数。

2、0既不是 数，也不是 数，但它是自然数】二、实数的基本概念和性质1、数轴：规定了 、 、 的直线叫做数轴， 和数轴上的点是一一对应的，数轴的作用有 、 、 等。

2、相反数：只有 不同的两个数叫做互为相反数，a 的相反数是 ，0的相反数是 ，a 、b 互为相反数⇔3、倒数：实数a 的倒数是 ， 没有倒数，a 、b 互为倒数⇔4、绝对值：在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。

a =因为绝对值表示的是距离，所以一个数的绝对值是 数，我们学过的非负数有三个： 、 、 。

【名师提醒：a+b 的相反数是 ，a-b 的相反数是 ,0是唯一一个没有倒数的数，相反数等于本身的数是 ，倒数等于本身的数是 ，绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。

1、科学记数法：把一个较大或较小的数写成 的形式叫做科学记数法。

其中a 的取值范围是 。

2、近似数和有效数字：一般的，将一个数四舍五入后的到的数称为这个数的近似数，这时，从 数字起到近似数的最后一位止，中间所有的数字都叫这个数的有效数字。

【名师提醒：1、科学记数法不仅可以表示较大的数，也可以表示较小的数，其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 （a ＞0） （a ＜0） 0 （a=0）范围一样，n 的取值不同，当表示较大数时，n 的值是原整数数位减一，表示较小的数时，n 是负整数，它的绝对值等于原数中左起第一个非零数字前零的个数（含整数数位上的零）。

第一讲 数与式1、 绝对值(1)绝对值的代数意义：正数的绝对值是它的本身，负数的绝对值是它的相反数,零的绝对值仍是零．即,0,||0,0,,0.a a a a a a >⎧⎪==⎨⎪-<⎩（2)绝对值的几何意义：一个数的绝对值，是数轴上表示它的点到原点的距离． （3）两个数的差的绝对值的几何意义：b a -表示在数轴上,数a 和数b 之间的距离．2、绝对值不等式的解法 （1）含有绝对值的不等式①()(0)f x a a <>，去掉绝对值后，保留其等价性的不等式是()a f x a -<<。

②()(0)f x a a >>，去掉绝对值后，保留其等价性的不等式是()()f x a f x a ><-或。

③22()()()()f x g x f x g x >⇔>。

（2)利用零点分段法解含多绝对值不等式：①找到使多个绝对值等于零的点．②分区间讨论，去掉绝对值而解不等式．一般地n 个零点把数轴分为n ＋1 段进行讨论． ③将分段求得解集，再求它们的并集． 例1。

求不等式354x -<的解集例2.求不等式215x +>的解集例3.求不等式32x x ->+的解集例4。

求不等式｜x ＋2｜＋｜x －1|＞3的解集．例5。

解不等式｜x －1|＋|2－x ｜＞3－x ．例6。

已知关于x 的不等式｜x －5|＋｜x －3|＜a 有解，求a 的取值范围． 练习解下列含有绝对值的不等式：（1）13x x -+-＞4+x（2）｜x +1｜<｜x －2| （3）｜x －1｜+|2x +1|<4 (4）327x -<（5)578x +>3、因式分解 乘法公式（1)平方差公式 22()()a b a b a b +-=- （2）完全平方公式 222()2a b a ab b ±=±+ (3)立方和公式 2233()()a b a ab b a b +-+=+ （4)立方差公式 2233()()a b a ab b a b -++=-（5）三数和平方公式 2222()2()a b c a b c ab bc ac ++=+++++ （6）两数和立方公式 33223()33a b a a b ab b +=+++ （7）两数差立方公式 33223()33a b a a b ab b -=-+-因式分解的主要方法有：十字相乘法、提取公因式法、公式法、分组分解法，另外还应了解求根法及待定系数法．1．十字相乘法 例1 分解因式：（1）x 2－3x ＋2； （2）2672x x ++（3)22()x a b xy aby -++； (4)1xy x y -+-．2．提取公因式法例2.分解因式:（1）()()b a b a -+-552(2）32933x x x +++3．公式法例3.分解因式： （1）164+-a （2）()()2223y x y x --+4．分组分解法例4.（1)x y xy x 332-+- （2）222456x xy y x y +--+- 5．关于x 的二次三项式ax 2+bx +c （a ≠0）的因式分解．若关于x 的方程20(0)ax bx c a ++=≠的两个实数根是1x 、2x ,则二次三项式2(0)ax bx c a ++≠就可分解为12()()a x x x x --.例5.把下列关于x 的二次多项式分解因式：（1）221x x +-; （2）2244x xy y +-．练习(1）256x x -- （2）()21x a x a -++ （3）21118x x -+（4)24129m m -+ （5)2576x x +- (6）22126x xy y +-(7）()()3211262+---p q q p (8）22365ab b a a +- (9)()22244+--x x（10）1224+-x x （11）by ax b a y x 222222++-+-（12）91264422++-+-b a b ab a （13）x 2－2x －1（14) 31a +； （15）424139x x -+;（16）22222b c ab ac bc ++++； （17)2235294x xy y x y +-++-第二讲 一元二次方程与二次函数的关系1、一元二次方程 （1)根的判别式对于一元二次方程ax 2＋bx ＋c ＝0（a ≠0），有：（1） 当Δ＞0时,方程有两个不相等的实数根x 1，2＝2b a-；（2）当Δ＝0时，方程有两个相等的实数根x 1＝x 2＝－2b a; （3）当Δ＜0时，方程没有实数根．(2）根与系数的关系（韦达定理)如果ax 2＋bx ＋c ＝0（a ≠0）的两根分别是x 1，x 2，那么x 1＋x 2＝b a -,x 1·x 2＝ca．这一关系也被称为韦达定理．2、二次函数2y ax bx c =++的性质1。

第一讲 数与式（2）学习目标1、 掌握各种乘法公式的书写，并会灵活运用。

2、 熟悉因式分解的一般步骤。

3、 掌握十字相乘法学习过程 一、 知识方法归纳 1、 乘法公式：1) 平方差公式： 2) 完全平方公式： 3) 立方和公式： 4) 立方差公式： 5) 三数和平方公式： 6) 两数和立方公式：2、分解因式：把一个多项式化成 ，这种变形叫做把这个多项式分解因式。

也叫 。

例如：3ax+3bx= 因式分解是对多项式进行的一种恒等变形，是整式乘法的逆过程。

3、因式分解的方法 1）提公因式法：①定义：如果多项式的各项有 ，可以把这个公因式提到 ，将多项式写成 的形式，这个变形就是提公因式法分解因式。

公因式：多项式的各项都含有的 。

公因式可以是一个数字或字母，也可以是一个单项式或多项式。

系数:取各项系数的最大公约数（什么是最大公约数？如何求最大公约数？） 字母:取各项都含有的字母 指数:取相同字母的最低次幂例如：123a 3b c +6422a b c —8323a b c 的公因式是 。

②提公因式的步骤 第一步：找出公因式；第二步：提公因式并确定另一个因式，提公因式时，可用原多项式除以公因式，所得商即是提公因式后剩下的另一个因式。

注意：提取公因式后，对另一个因式要注意整理并化简，务必使因式最简。

多项式中第一项有负号的，要先提取符号。

例1、把—122a b —182ab —2433a b 分解因式.例2、把多项式3（x-4）+x(4-x)分解因式（2）运用公式法定义：把乘法公式反过来用，就可以用来把某些多项式分解因式，这种分解因式的方法叫做运用公式法。

逆用平方差公式:逆用完全平方公式： 注意：①公式中的字母可代表一个数、一个单项式或一个多项式。

②选择使用公式的方法：主要从项数上看，若多项式是二项式可考虑平方公式；若多项式是三项式，可考虑完全平方公式。

例如：因式分解2a -14a+494、 十字相乘法：首项系数为一的二次多项式2()()()x p q x pq x p x q +++=++方法：常数项分成p 和q ， p+q 为一次项系数xxp q例如：230x x --二、当堂测试1.分解因式4353x x x ++2.分解因式：2m n n -= _______ ．3.因式分解2310x x +-4．分解因式：(1)=-a a 422；(2)269a a -+=5.已知ab= -1,a+b=2，则式子b a a b +=。

第一讲 数与式一、学习指引1.知识要点（1）运算与运用（2）数的规律探究（3）新背景下的数的运算 （4）整式、分式、二次根式（5）代数式的值 2.方法指导（1）巧算要注意算式的特点，运用运算律适当更换次序，使计算简便，平时要不断归纳拆、拼、凑整、交换等运算技巧.（2）数的规律探究主要是解题的过程中去找出内在的规律（3）解决定义新运算的问题，关键是通过新运算的定义，将新运算转化为常规运算. （4）对于代数式的化简、求值，常用到的技巧有：①因式分解，对所给的条件、所求的代数式实施因式分解，达到化繁为简的目的； ②运算律，适当运用运算律，也有助于化简； ③换元、配方、待定系数法、倒数法等；④有时对含有根式的等式两边同时实施平方，也不失为一种有效的方法.二、典型例题例1.计算（1）99163135115131++++ （2）（21＋31＋……＋20021）（1＋21＋31＋……＋20011）－（1＋21＋31＋......＋20021）（21＋31＋ (20011)（3）设22211148()34441004A =⨯++---，则与A 最接近的正整数是（ ） A.18 B.20 C.24 D.25例2.（1）化简：22221369x y x y x y x xy y+--÷--+＝_______ ； (2)若x 2－2y ＋6x ＋10＋y 2=0,则223442xyy x x yx +--=__________；(3)已知)0,0(02>>=+-y x y xy x ，则yxy x y xy x 4353-++-的值为 ( )A ．31 B ．21 C ．32D ．43(4)已知b a x -=c b y-=ac z -,那么x+y+z= ； (5)当x 依次取1，2，3， (2009)1 2， 1 3， 1 4，…， 1 2009时，代数式 x 21＋x 2的值的和等于 ；例3（1）将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，……，依次规律，第6个图形有 个小圆.（2）一串数1，1，1，2，2，3，4，5，7，9，12，16，21，……称为帕多瓦数列，请根据这个数列的一个规律，写出其中的第19个数是 ．（3）将正整数按如图所示的规律排列下去，若有序实数对（n ，m ）表示第n 排，从左到右第m 个数，如（4，2）表示9，则表示58的有序数对是（ ） A.（11，3） B.（3，11） C.（11，9） D.（9，11）(4)如图，是用棋子摆成的图案，摆第1个图案需要7枚棋子，摆第2个图案需要19枚棋子，摆第3个图案需要37枚棋子，按照这样的方式摆下去，则摆第6个图案需要 枚棋子，摆第n 个图案需要 枚棋子．第1个图形 第2个图形 第3个图形 第4个图形……图4例4（1）刘谦的魔术表演风靡全国，小明也学起了刘谦发明了一个魔术盒，当任意实数对（a ，b ）进入其中时，会得到一个新的实数：a 2+b -1，例如把（3，-2）放入其中，就会得到32+（-2）-1=6.现将实数对（m ，-2m ）放入其中，得到实数2，则m = ． (2)阅读材料，寻找共同存在的规律：有一个运算程序a ⊕b=n ，可以使：（a+c ）⊕b= n+c ，a ⊕（b+c ）=n －2c ，如果1⊕1=2，那么2010⊕2010 = ．(3)若f (x )=x +3，f 1 (x )=f (x )，f 2 (x )=f (f 1 (x ))，f 3 (x )=f (f 2 (x ))，…，f 2k +1 (x )=f (f k (x ))，则f 1 (1)+ f 2 (2)+ f 3 (3)+…+f 100 (100)=例5(1)电子跳蚤游戏盘是如图所示的△ABC ，AB =AC =BC =6．如果跳蚤开始时在BC 边的P 0处，BP 0=2．跳蚤第一步从P 0跳到AC 边的P 1（第1次落点）处，且CP 1= CP 0；第二步从P 1跳到AB 边的P 2（第2次落点）处，且AP 2= AP 1；第三步从P 2跳到BC 边的P 3（第3次落点）处，且BP 3= BP 2；…；跳蚤按照上述规则一直跳下去，第n 次落点为P n （n 为正整数），则点P 2009与点P 2010之间的距离为_________．(2)如图，在平面直角坐标系xOy 中，等腰梯形ABCD 的顶点坐标分别为A （1，1），B （2，－1），C （－2，－1），D （－1，1）．y 轴上一点P （0，2）绕点A 旋转180°得点P 1，点P 1绕点B 旋转180°得点P 2，点P 2绕点C 旋转180°得点P 3，点P 3绕点D 旋转180°得点P 4，……，重复操作依次得到点P 1，P 2，…， 则点P 2010的坐标是（ ）． A.（2010，2） B.（2010，2-） C.（2012，2-） D.（0，2）(3)在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为（1，0），点DA BCP 0 P 1P 2P 3第6(1)题图第6(2)题图的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；延长C 1B 1交x 轴于点A 2，作正方形A 2B 2C 2C 1…按这样的规律进行下去，第2010个正方形的面积为( ) A ．2009235⎪⎭⎫ ⎝⎛ B ．2010495⎪⎭⎫⎝⎛C ．2008495⎪⎭⎫ ⎝⎛ D ．4018235⎪⎭⎫⎝⎛(4)一个一次函数的图象与直线y ＝45x ＋495平行，与x 轴、y 轴的交点分别为A 、B ，并且过点（-1，-25），则在线段AB 上（包括点A 、B ），横、纵坐标都是整数的点有多少个？第6(3)题图4=1+3 9=3+616=6+10…第一讲 实数同步练习活动基地 班级 姓名【基础巩固】一、选择题1. 若的值为则2y-x 2,54,32==yx( )A.53 B.-2 C.553 D.562. 已知a －b=b －c=52，a 2＋b 2＋c 2=1则ab ＋bc ＋ca 的值等于 （ ） Ａ.2513 Ｂ.2512 Ｃ.53 Ｄ.523．古希腊著名的毕达哥拉斯学派把1、3、6、10… 这样的数称为“三角形数”，而把1、4、9、16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻 “三角形数”之和．下列等式中，符 合这一规律的是（ ） A ．13 = 3+10B ．25 = 9+16C ．36 = 15+21D ．49 = 18+314．观察以下数组：（1），（3、5），（7、9、11），（13、15、17、19），…问2009在第（ ）组．Ａ．44 Ｂ． 45 Ｃ．46 Ｄ．47 5．若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式．．．．．，如a b c ++就是完全对称式.下列三个代数式：①2)(b a -；②ab bc ca ++；③222a b b c c a ++．其中是完全对称式的是( )A ．①②B ．①③C ． ②③D ．①②③6．某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k 棵树种植在点)(k k k y x P ，处，其中11=x ，11=y ，当k ≥2时，⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ，[a ]表示非负实数a 的整数部分，例如[2.6]=2，[0.2]=0.按此方案，第2009棵树种植点的坐标为A.（5，2009）B.（6，2010）C.（3，401）D.（4，402） 7.下面是按一定规律排列的一列数：第1个数：11122-⎛⎫-+ ⎪⎝⎭；第2个数：2311(1)(1)1113234⎛⎫⎛⎫---⎛⎫-+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭； 第3个数：234511(1)(1)(1)(1)11111423456⎛⎫⎛⎫⎛⎫⎛⎫-----⎛⎫-+++++ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭； ……第n 个数：232111(1)(1)(1)111112342n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭．那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是 （ ）A ．第10个数B ．第11个数C ．第12个数D ．第13个数二、填空题8.观察下表，回答问题：第 个图形中“△”的个数是“○”的个数的5倍9.如图（1），已知小正方形ABCD 的面积为1，把它的各边延长一倍得到新正方形A 1B 1C 1D 1；把正方形A 1B 1C 1D 1边长按原法延长一倍得到正方形A 2B 2C 2D 2（如图（2））；以此下去···，则正方形A 4B 4C 4D 4的面积为__________,正方形A n B n C n D n 的面积为__________．第9题图（1） A 1B 1C 1D 1 A B C D D 2 A 2 B 2C 2D 1 C 1B 1A 1 ABCD 第9题图（2）10.已知21(123...)(1)n a n n ==+，，，，记112(1)b a =-，2122(1)(1)b a a =--，…，122(1)(1)...(1)n n b a a a =---，则通过计算推测出n b 的表达式n b ＝_______．11．已知25350x x --=，则22152525x x x x --=-- ． 12.正方形A 1B 1C 1O ，A 2B 2C 2C 1，A 3B 3C 3C 2和点C 1，C 2，C 3，…分别在直线y kx b =+(k ＞0)和x 轴上， 已知点B 1(1，1)，B 2(3，2)， 则B n 的坐标是______________．三、解答题13.已知0|2|1=-+-xy x ，求)2009)(2009(1)1)(1(11+++++++y x y x xy 的值.14.若4x －3y －6z=0,x+2y －7z=0 (xyz ≠0),求代数式222222103225zy x z y x ---+的值.【能力拓展】15.对任意实数x 、y ，定义运算x *y 为x *y=ax+by+cxy 其中a 、b 、c 为常数，等式右端运算是通常的实数的加法和乘法．现已知1*2=3，2*3=4，并且有一个非零实数d ，使得对于任意实数x,都有x *d=x ，求d 的值．16.类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为 3+（2-）=1．若坐标平面上的点作如下平移：沿x 轴方向平移的数量为a （向右为正，向左为负，平移a 个单位），沿y 轴方向平移的数量为b （向上为正，向下为负，平移b 个单位），则把有序数对{a ，b }叫做这一平移的“平移量”；“平移量”{a ，b }与“平移量”{c ，d }的加法运算法则为}{}{}{d b c a d c b a ++=+，，，． 解决问题：（1）计算：{3，1}+{1，2}；{1，2}+{3，1}．（2）①动点P 从坐标原点O 出发，先按照“平移量”{3，1}平移到A ，再按照“平移量”{1，2}平移到B ；若先把动点P 按照“平移量”{1，2}平移到C ，再按照“平移量” {3，1}平移，最后的位置还是点B 吗? 在图1中画出四边形OABC . ②证明四边形OABC 是平行四边形.（3）如图2，一艘船从码头O 出发，先航行到湖心岛码头P （2，3），再从码头P 航行到码头Q （5，5），最后回到出发点O . 请用“平移量”加法算式表示它的航行过程．（第22图1。