拉格朗日方程与哈密顿方程(仲顺安)资料.

经典力学的拉格朗日与哈密顿形式经典力学是物理学中的一个重要分支，用来研究物体在作运动时的力学规律。

在经典力学的发展历程中，拉格朗日力学和哈密顿力学是两个基本的理论框架。

本文将对拉格朗日力学和哈密顿力学的基本概念、原理和应用进行介绍。

一、拉格朗日力学拉格朗日力学是由意大利数学家拉格朗日于18世纪提出的一种描述力学系统的方法。

它基于一个称为“拉格朗日函数”的函数来描述物体的运动。

拉格朗日函数由广义坐标和广义速度构成，具体形式为L(q, ẋ)，其中q表示广义坐标，ẋ表示广义速度。

在拉格朗日力学中，通过引入一个称为“作用量”的量来描述系统的运动。

作用量定义为物体在运动过程中受到的广义力与广义坐标变化的积分，即S = ∫L(q, ẋ)dt。

拉格朗日原理指出，物体在运动时，其实际路径是使作用量S取极值的路径。

通过应用拉格朗日原理，可以得到运动方程及其解。

对于单个质点的运动，拉格朗日力学方程可以写为∂L/∂q - d(∂L/∂ẋ)/dt = 0。

对于多个质点的系统，可以将拉格朗日函数写为各质点的质量、速度以及势能、动能的函数，并将系统的位形空间表示为广义坐标的空间。

拉格朗日力学具有坐标变换不变性、方程形式简洁等优点，适用于描述各种复杂力学系统的运动。

二、哈密顿力学哈密顿力学是由爱尔兰物理学家威廉·哈密顿于19世纪提出的一种力学描述方法。

它是拉格朗日力学的一种等价形式，通过引入广义动量，将力学系统的描述从坐标空间转化为相空间。

在哈密顿力学中，广义动量定义为p = (∂L/∂ẋ)，并利用广义动量和广义坐标构成哈密顿函数H(q, p)。

哈密顿函数描述了系统的总能量，并在相空间中表示系统的状态。

利用哈密顿原理，可以推导出哈密顿力学的运动方程，即哈密顿正则方程。

对于单个质点的运动，哈密顿正则方程写为dq/dt = (∂H/∂p)，dp/dt = - (∂H/∂q)。

对于多个质点的系统，可以将哈密顿函数表示为各质点坐标、动量以及势能、动能的函数。

拉格朗日方程拉格朗日方程(Lagrange Equations)是描述质点系统在广义坐标下的运动的一种方法。

它是由意大利数学家拉格朗日在1755年提出的。

拉格朗日方程是一种非常有用的方法，可以用来解决复杂的力学问题。

本文将阐述拉格朗日方程的概念、定义、推导和应用。

一、拉格朗日方程的概念拉格朗日方程是一种描述物理系统的运动的数学工具。

它是在广义坐标系下描述系统的运动的。

广义坐标系是指可以描述系统运动的坐标系，与传统的笛卡尔坐标系不同。

拉格朗日方程允许我们用少量的代数方程式描述物理系统的运动，而不必考虑物体的确切轨迹。

二、拉格朗日方程的定义拉格朗日方程可以用来描述质点系统的运动。

一个质点系统是由一些质点组成的体系，它们在一起相互作用并受到外力的作用。

拉格朗日方程消除了这些参与到系统运动中的力，并通过一组数学公式描述质点的运动。

这些公式通常由拉格朗日函数和广义坐标定义。

三、拉格朗日方程的推导假设有一个质点系统，它包含了n个质点。

每个质点都有质量m(i)，位于位置向量r(i)。

一个质点所受的总力为F(i)，则拉格朗日函数为：L = T - V其中，T表示动能，V表示势能，它们都是广义坐标的函数，正好表示质点的位置。

T的公式为：T = 1/2 m(i)*v(i)^2其中，v(i)表示第i个质点的速度向量。

势能V可以描述整个质点系统的势能。

假设在质点系统中有m个约束条件C(k)，它们是广义坐标q的函数，如C(k)(q) = 0。

约束条件通常是描述系统中相互作用的限制条件。

根据达朗贝尔原理，可以推导出拉格朗日方程的表达式。

达朗贝尔原理是指系统中所有质点所受力的合力是零，即：∑F(i) = 0假设广义坐标为q = (q1, q2, …, qn)，其变化率为dq(i)/dt。

则对于所有的i，可以得到：F(i) = m(i) d^2r(i)/dt^2然后对约束条件C(k)求偏微分：∂C(k) / ∂ri * d^2ri/dt^2 + ∂C(k) / ∂rj * d^2rj/dt^2 = 0其中，i和j分别代表C(k)所属于的质点。

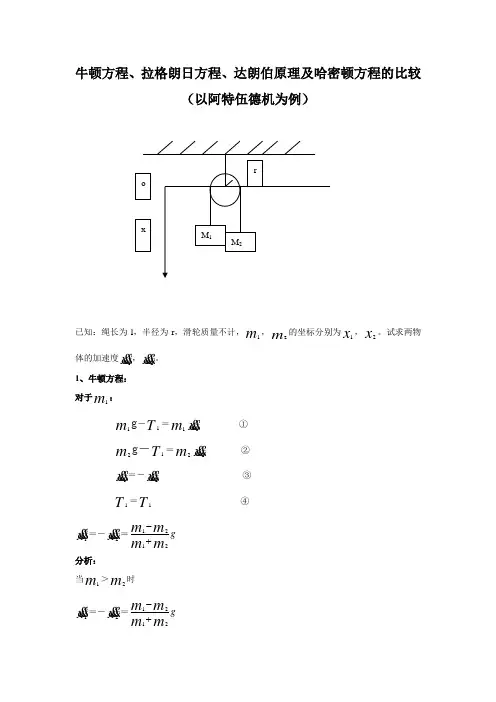
牛顿方程、拉格朗日方程、达朗伯原理及哈密顿方程的比较（以阿特伍德机为例）已知：绳长为l ，半径为r ，滑轮质量不计，1m ，2m 的坐标分别为1x ，2x 。

试求两物体的加速度1x ，2x 。

1、牛顿方程： 对于1m ：1m g －1T＝1m 1x① 2m g －1T ＝2m 2x②1x＝－2x ③ 1T＝1T ④1x ＝－2x＝1212g m m mm-+分析： 当1m ＞2m 时1x ＝－2x ＝1212g mm mm-+当1m ＜2m 时1x ＝－2x ＝2112g mm mm-+当1m ＝2m1x＝－2x ＝02、拉格朗日方程0dL L dt q q αα⎛⎫∂∂ ⎪-= ⎪∂∂⎝⎭势能零点为坐标轴X 轴零点处 T ＝21112m v －22212m v ＝21112m x －22212m x＝()()21211212mm xx x +=-U ＝()11221g g l r m x m x x π----L T U =- ()()2121112112g g l r m m xm x mx π=+++-- ()121L m m x q α∂=+∂1L x ∂=∂ （广义动量）12L g g m m qα∂=-∂1L x ∂=∂（广义力）固有：()()121120g m m x m m ---= 3、达朗伯原理首先，推导虚功原理虚位移：0t δ=虚功（约束力）=0→理想约束 在牛顿力学中有，当1m =2m 时0iiN F -= ()0ii irN F δ-=虚功原理：0i ir Fδ∙=∑（平衡条件）拉格朗日平衡：dL L L U dt q q q ααα⎛⎫∂∂∂ ⎪==- ⎪∂∂∂⎝⎭如果一个系统处于平衡状态，则势函数有极值，有极小值则出现稳定平衡且稳定平衡是力学中存在的平衡。

动力学原理：2iiiim x N F -= 20iiiim x N F --=达朗伯原理：()20ii i i im x r NF δ--=4、哈密顿方程①广义动力()L T U =-()22212T myxz=++xT m xxP∂==∂ 同理有yT m yyP∂==∂ ，zT m zzP∂==∂即是：xL m xxP∂==∂ 同理有yL myyP∂==∂ ，zL m zzP∂==∂②勒让德变换 设函数(),f x y 令f X x∂=∂，f Y y∂=∂对于函数(),f x y 的全微分f f df dx dy Xdx Ydy xy∂∂=+=+∂∂令()(),,G X Y f x y xX yY =-- ()()(),dG X Y df d xX d yY =--d f X d x x d X Y d y y=---- x d X y d Y =-- ① 而G G dG dX dY XY∂∂=+∂∂ ②由①②可以得：G x X∂=-∂G y Y∂=-∂在拉格朗日方程中： (),Lqq αα LP q αα∂=∂ ()11sH L qP ααα=⎛⎫=--- ⎪⎝⎭∑ 哈密顿函数 ()1,sHL qq PPααααα==-+∑（,q P αα为共轭变量）()11,ssH HdHd d q q P P qP αααααααα==∂∂=+∂∂∑∑()1111,ssssLLdHd d d d qq q q qP P P q q αααααααααααααα====⎛⎫∂∂⎛⎫ ⎪=-+++⎪ ⎪∂∂⎝⎭⎝⎭∑∑∑∑ H L qqαα∂∂=-∂∂ ③H qP αα∂=∂ ④ 由拉格朗日得L P q αα∂=∂ ⑤LP qαα∂=∂ ⑥由③④⑤⑥可以得到：H Pqαα∂=-∂ （广义力）H qP αα∂=∂ （广义速度） 由哈密顿求解阿特伍德机：()()2121112112H g g l r mm xm xm x π=+----()12121H g g g m mm m x ∂=-+=--∂()1211H m m x P x α∂=-=∂()12111H H mm xPx x α⎛⎫∂∂==+⎪ ⎪∂∂⎝⎭故由哈密顿方程可以得到：121112H g m mx Pm x m α-∂=-→=∂+分析力学的优点：消去“理想约束”减少方程数量，进而减少计算量。

拉格朗日方程推导1. 引言拉格朗日方程是经典力学中的重要工具，用于描述质点、刚体或者连续体的运动。

它是以法国数学家约瑟夫·路易·拉格朗日（Joseph Louis Lagrange）的名字命名的，是一种基于能量原理的变分方法。

通过使用拉格朗日方程，我们可以从一个系统的动能和势能推导出该系统的运动方程。

本文将详细介绍拉格朗日方程的推导过程，并给出一些实际问题的例子来说明其应用。

2. 基本概念在开始推导拉格朗日方程之前，我们需要了解几个基本概念：2.1 广义坐标广义坐标是描述系统状态的变量，可以是位置、角度或者其他合适的参数。

我们用q i表示第i个广义坐标，其中i可以是1、2、3…n。

2.2 广义速度广义速度是广义坐标随时间变化的导数，用q̇i表示。

2.3 广义动能广义动能表示系统中所有质点（或刚体）运动所具有的总能量。

对于质点而言，广义动能可以写作T=12mq̇2，其中m是质点的质量。

对于刚体或连续体而言，广义动能的表达式会有所不同。

2.4 广义势能广义势能表示系统中所有与位置相关的势能总和。

用V表示。

3. 拉格朗日方程的推导拉格朗日方程的推导基于哈密顿原理（或称为最小作用量原理）。

哈密顿原理认为，在所有可能的路径中，真实的路径是使作用量S取极小值的路径。

3.1 作用量作用量是描述系统在一段时间内经历的运动轨迹所需要付出的代价。

对于一段时间从t1到t2内，系统在广义坐标q i(t)下进行运动，其作用量可以表示为：S=∫(T−V)t2t1dt其中T是广义动能，V是广义势能。

3.2 哈密顿原理根据哈密顿原理，真实路径所对应的作用量S必须满足变分条件：δS=δ∫(T−V)t2t1dt=0我们可以将变分操作放在积分符号内部：∫(δT−δV)t2t1dt=03.3 变分操作我们对广义坐标q i(t)进行微小变动δq i(t)，则广义速度q̇i的变化量可以表示为：δq̇i=ddt (δq i)根据链式法则，上式可以改写为：d dt (δq i)=∂∂t(δq i)+∑∂q j∂tnj=1∂∂q j(δq i)3.4 广义速度的变分我们可以将广义速度的变分表示为：δq̇i=∂∂t(δq i)+∑q̇jnj=1∂∂q j(δq i)3.5 广义动能的变分广义动能的变分可以表示为：δT=∑[∂T∂q iδq i+∂T∂q̇iδq̇i]n i=1=∑[∂T∂q iδq i+mq̈i(t)δq i]n i=1=∑[∂T∂q i−ddt(∂T∂q̇i)]ni=1δq i 3.6 广义势能的变分广义势能的变分可以表示为：δV=∑∂V ∂q ini=1δq i 3.7 拉格朗日方程的推导将3.5和3.6两式代入3.2，我们得到：∫[∑(∂T∂q i−ddt(∂T∂q̇i))ni=1−∑∂V∂q ini=1]t2t1δq i dt=0由于δq i是任意的，上式中括号内的表达式必须为零，即：∑(∂T∂q i−ddt(∂T∂q̇i))ni=1−∑∂V∂q ini=1=0这就是拉格朗日方程。

简论哈密顿力学的和拉格朗日力学几何的差异性翻开大多数海内外的一本中级理论物理学教材（即本科高年级和硕士低年级），都是简要地回顾了一下牛顿力学（包括拉格朗日力学在内）和哈密顿力学两种力学的所谓的“物理学”差异性，几乎从不论述它们二者的几何学差别性。

而有的美国教授正确地说道，把在一个正交空间中展现的牛顿力学，放进两个互为倒易的斜交空间重新表述出来的力学就是拉格朗日力学。

可是，却没有把“牛顿力学和哈密顿力学的几何差别”陈述出来。

当然，在高等物理学的教材（硕士高年级和博士年级）中，很多国内外的作者几乎是清一色地把“哈密顿力学和拉格朗日力学的差别”诠释为“余切丛和切丛上的函数”（微分几何中，一个微分流形的余切丛是流形每点的余切空间组成的向量丛；一个微分流形的切丛是一个由流形各点上切空间组成的向量丛，其总空间是各切空间的不交并集），固然这是正确滴。

可是，切丛和余切丛的关系又是什么呢？呵呵，遗憾的是几乎没有一个专著明确指出和推导。

仿佛我们除了只有一个“勒让德变换”来从数学上来连接“哈密顿力学和拉格朗日力学”之外，再就无能为力了！然而，更重要的问题却是：“同一个物理学质点的几何模型，真的会有任何物理学上的差别吗？”换言之，当我们选择不同的数学几何学来描述在光滑自由空间中同一个物理质点的加速运动的时候，无疑地将产生数学上的形式差别，可是这会出现物理学上的本质差别吗？欧几里德几何学比较特殊，它是在笛卡尔正交坐标系里展开讨论的。

这是牛顿力学首选的数学模型，人人对它都耳熟能详。

碰巧的是，它的两个左右共轭的空间恰好一模一样，镜像一般而无需任何区分。

正是这个特点，让我们觉得欧几里德几何学是在自然那不过的，并且直觉上感到这是很简单、又很真实的几何学。

欧几里德几何学是仿射几何学的一个子几何，它可以被称作是“正交几何学”；而仿射几何学也可以称作是“斜交几何学”。

显而易见的是正交的欧几里德几何学是斜交的仿射几何学的一个子几何，因为假如坐标系的个坐标轴恰好是正交的——即彼此相互垂直的话，这时的仿射几何学依旧是仿射几何学，但是，同时还可以被称作是欧几里德几何学了。

拉格朗日量、哈密顿量及变分原理牛顿力学大家非常熟悉，但是我们仔细思考会发现，牛顿的理论并没有对这个世界的本质进行建模分析，它的三定律只能算是表象级的描述，现在我们来学习一种新的模型，这种模型本质上与牛顿力学相等价，但是在形式上有所不同，并且便于推广到物理学的其他各门分支，我们称之为拉格朗日力学。

拉格朗日力学认为，一切经典力学的规律可以通过称之为最小作用量原理的一种方式导出，对每一个物理体系，我们有一个称之为作用量的物理参量，我们选取时间作为参数，则另有一个称为朗格朗日量的参量，假定我们已经知道了一个物理系统必定会随时间经历两个确定的物理状态，那么以这两个状态为起始与终末对拉格朗日量进行积分将会得到对应的作用量，而真实的物理过程对应的数学方程将会是作用量取极值时拉格朗日量中各参的关系。

需要说明的是，作用量实质上是拉格朗日量的泛函，而他取极值的方式是通过变分原理。

首先我们给出变分原理的作用形式，我们用A和B来表征一个物理系统的起始与终末状态。

欧拉-拉格朗日方程就是最小作用量原理工作的形式，接下来我们直接给出一些经典体系的拉格朗日量，并且通过变分原理验证拉格朗日力学确实与牛顿力学等价。

自由质点：由这几个例子可以知道，拉格朗日力学确实与牛顿力学等价，但是他们的作用形式非常的不同。

接下来我们介绍另一个等价描述方式，称之为哈密顿力学，哈密顿力学描述物理系统的方式是通过哈密顿方程组。

现在我们由拉格朗日量导出哈密顿量：由定义可知，哈密顿量表征的物理意义是能量，最后一个由微分方程导出的方程组就是哈密顿方程组。

从导出的过程来看我们已经知道了，哈密顿力学与拉格朗日力学相等价。

从作用形式来看，拉格朗日力学的欧拉-拉格朗日是二阶方程组，因为其中可能含有q的二阶导数，而哈密顿力学的哈密顿方程组是一阶方程组，但是自变量变成了原来的两倍（动量p也成了变量）。

哈密顿原理虽然是由经典力学发现出来的，但是它的应用范围却极大的扩展到其他的领域，后续将进行进一步的介绍。

拉格朗日方程推导标题:拉格朗日方程的推导及应用简介:拉格朗日方程是经典力学中一种重要的数学工具，用于描述质点、刚体和连续介质系统的运动。

本文将详细介绍拉格朗日方程的推导过程，并探讨其在物理学中的应用。

正文:拉格朗日方程是由法国数学家约瑟夫·路易斯·拉格朗日于18世纪提出的，它是一种基于能量原理的分析方法。

拉格朗日方程在处理多自由度系统时非常有用，能够简化复杂的运动方程，使问题的求解更加方便。

为了推导拉格朗日方程，我们需要定义系统的拉格朗日函数。

拉格朗日函数通常用L来表示，它是广义坐标q_i和广义速度v_i的函数，即L(q_i,v_i)。

拉格朗日函数的定义如下：L(q_i,v_i)=T(q_i,v_i)-U(q_i)其中，T(q_i,v_i)表示系统的动能，U(q_i)表示系统的势能。

动能T是广义速度v_i的函数，势能U是广义坐标q_i的函数。

接下来，我们将利用哈密顿原理来推导拉格朗日方程。

哈密顿原理指出，在运动过程中，系统的真实轨迹是使作用量S达到极小值的路径。

作用量S定义为：S=∫L(q_i,v_i)dt其中，积分是在整个运动过程中进行的。

为了使作用量S达到极小值，我们需要对广义坐标q_i进行变分，即δq_i。

根据变分法则，我们可以得到：δS=∫(∂L/∂q_i-d/dt(∂L/∂v_i))δq_i dt根据哈密顿原理，δS必须为零，因此上式中的被积函数必须为零。

我们可以得到拉格朗日方程的形式：∂L/∂q_i-d/dt(∂L/∂v_i)=0这就是拉格朗日方程的一般形式。

对于多自由度系统，有多个广义坐标和广义速度，我们可以得到对应的一组拉格朗日方程。

拉格朗日方程的推导过程相对简单，但其应用范围非常广泛。

通过求解拉格朗日方程，我们可以得到系统的运动方程，进一步研究物体的运动规律和力学性质。

此外，拉格朗日方程还在其他领域有着重要应用，例如电磁学、光学和量子力学等。

总结:本文详细介绍了拉格朗日方程的推导过程，并探讨了其在物理学中的应用。