测量学 第五章 测量误差理论基础
- 格式:pdf
- 大小:1.77 MB
- 文档页数:36
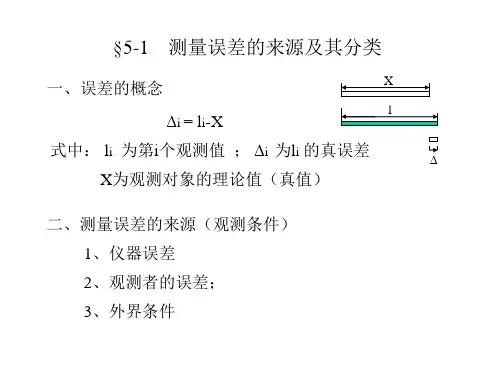


现在的位置:课程介绍 >> 理论部分 >> 电子讲稿第五章误差基本知识5.1误差的来源和分类一、定义:观测值与真值之差,记为:X为真值,即能代表某个客观事物真正大小的数值。
为观测值,即对某个客观事物观测得到的数值。
为观测误差,即真误差。
二、误差的来源1、测量仪器一是仪器本身的精度是有限的,不论精度多高的仪器,观测结果总是达不到真值的。
二是仪器在装配、使用化、松动或装配不到位使得仪器存在着自身的误差。
如水准仪的水准管轴不平行视准轴,使得水准管气泡居中后,视线并不水平。
水准尺刻划不均匀使得读数不准确。
又如经纬仪竖盘指标差都是仪器本身的误差。
2、观测者是由于观测者自身的因素所带来的误差,如观测者的视力、观测者的经验甚至观测者的责任心都会影响到测举例:如水准尺倾斜、气泡未严格居中、估读不准确、未精确瞄准目标都是观测误差。
3、外界条件测量工作都是在一定的外界环境下进行的。
例如温度、风力、大气折光、地球曲率、仪器下沉都会对观测结上述三项合称为观测条件a.等精度观测:在相同的观测条件下进行的一组观测。
b.不等精度观测:在不同的观测条件下进行的一组观测。
测量误差的分类根据测量误差表现形式不同,误差可分为系统误差、偶然误差和粗差。
1、系统误差定义:误差的符号和大小保持不变或者按一定规律变化,则称其为系统误差。
如:钢尺的尺长误差。
一把钢尺的名义长度为30m,实际长度为30.005m,那么用这把钢尺量距时每量一个整尺段距离就量短的量距误差,而且量取的距离越长,尺长误差就会越大,因此系统误差具有累计性。
如:水准仪的i角误差,由于水准管轴与视准轴不平行,两者之间形成了夹角i,使得中丝在水准尺上的读数不准确。
如果水差就会越大。
由于i角误差是有规律的,因此它也是系统误差。
正是由于系统误差具有一定的规律性,因此只要找到这种规律性,就可以通过一定的方法来消除或减弱系统具体措施有:(1)采用观测方法消除:如水准仪置于距前后水准尺等距的地方可以消除i角误差和地球曲率的影响。




习题五一、填空题1、真误差是指,其表达式为。
2、误差的来源有、、三个方面,按误差的性质不同,可分为和两种。
3、评定观测值精度主要采用、和。
4、用6″级经纬仪按测回法测量某一角度,欲使测角精度达到±5″,则测回数不得少于。
5、在等精度观测中,设观测值中误差为m,观测次数为n,则最可靠值的中误差为。
6、水准测量中,设一测站的高差观测中误差为±5mm,若1km有15个测站,则1km的高差中误差为。
7、误差传播定律是描绘和中误差关系的定律,它的表达式为。
8、在等精度观测平差中,最可靠值采用,其表达式为,在不等精度观测平差中,最可靠值采用,其表达式为。
9、在一组观测值中,单位权中误差为±3mm,某观测值的权为4,则该观测值中误差为。
二、简答题1、何为系统误差?它有什么特性?在测量工作中如何消除或削弱?2、何为偶然误差?偶然误差能否在测量工作中消除?它的统计特性有哪些?3、什么叫中误差?为什么中误差能够作为衡量精度的标准?在一组等精度观测中,中误差和真误差有何区别?4、试用偶然误差的特性来证明:在等精度观测中,算术平均值作为最可靠值。
5、设有Z1=X1+X2,Z2=2X3,若X1、X2、X3均独立,且中误差相等,问Z1、Z2的中误差是否相等,说明原因。
6、什么叫做权?它有什么含义?权与中误差之间的关系怎样?7、已知某正方形,若用钢尺丈量一条边,其中误差为m=±3mm,则正方形的周长中误差为多少?若用钢尺丈量4条边,则周长的中误差又是多少?试计算说明。
8、什么叫做权倒数传播定律?它描绘的是一种什么关系?它与误差传播定律有什么联系?三、选择题1、用水准仪观测时,若前、后视距不相等,此因素对高差的影响表现为(),在一条水准线路上的影响表现为()A 、偶然误差,偶然误差B 、偶然误差,系统误差C 、系统误差,偶然误差D 、系统误差,系统误差2、当误差的大小与观测量的大小无关时,此时不能用()来衡量精度A 、相对误差B 、中误差C 、绝对误差D 、容许误差()3、用30 米长的钢尺丈量距离(该尺经过检验后其实长度为29.995m ),用此尺每量一整尺就有0.005m 的尺长误差,则这种误差属于A 、偶然误差,且符号为(-)B 、系统误差,且符号为(-)C 、偶然误差,且符号为(+ )D 、系统误差,且符号为(+ )4、由于测量人员的粗心大意,在观测、记录或计算时读错、记错、算错所造成的误差,称为()A 、偶然误差B 、系统误差C 、相对误差D 、过失误差5、在相同条件下,对任何一个量进行重复观测,当观测次数增加到无限多时,偶然误差的算术平均值为零,这说明偶然误差具有A、对称性B、有界性 C 、大小性D、抵偿性6、中误差反映的是()。

第五章测量误差基本知识一、名词解释1.中误差[南京师范大学2011年]答:中误差是衡量观测精度的一种数字标准,又称“标准差”或“均方根差”,是指在相同观测条件下的一组真误差平方中数的平方根。
2.误差传播定律[东北大学2015年]答:误差传播定律是指反映观测值的中误差与观测值函数的中误差之间关系的定律,它根据函数的形式把函数的中误差以一定的数学式表达出来。
3.偶然误差答:偶然误差是指在相同的观测条件下,对某一量进行一系列的观测,误差出现的符号和数值大小都不相同,从表面上看没有任何规律性的误差。
4.系统误差答:系统误差是指在相同的观测条件下,对某一量进行一系列的观测,出现的符号和数值上相同,或按一定的规律变化的误差。
二、填空题1.精度的3个标准是,,。
【答案】中误差;相对误差;极限误差2.中误差作为极限误差。
【答案】2倍【解析】根据极限误差的定义,常把2倍中误差作为极限误差。
3.已知X=L1+L2,Y=(L1+L2)/2,Z=X·Y。
L1、L2中误差均为m,则X、Y、Z的中误差分别为,,。
【答案】m2;22m;22m4.某平面三角形中,观测了α、β两个内角,其测角中误差均为±6″,则此三角形第三个内角γ的中误差为。
【答案】±8.5″5.现有DJ6的经纬仪,用测回法观测一个角,要使测角中误差达到±6”,求至少要观测测回。
【答案】32【解析】该题考点是第五章误差理论,要理解6的含义,6指一测回方向观测的中误差,根据协方差传播率可求得测回数。
三、判断题1.广义算术平均值的权,不等于观测值权之和。
()【答案】错误【解析】不等精度观测值的加权平均值计算公式可以写成线性函数的形式:,根据线性函数的误差传播公式,得:,按式,以(m为单位权中误差),得:。
按式,加权平均值的权即为观测值的权之和:。
2.当每公里水准测量的精度相同时,水准路线观测高差的权与路线长度成正比。
()【答案】错误【解析】“权”的原来意义为秤锤,用做“权衡轻重”之意。


第五章 测量误差及测量平差§5.1 测量误差概述一、测量误差的概念某量的各测量值相互之间或观测值与理论值之间的往往存在着某些差异,说明观测中存在误差。
观测值与真值之差称为测量误差,也叫真误差。
X l i i -=∆ (i =1、2、……、n ) X 为真值。
二、研究测量误差的目的分析测量误差的产生原因、性质和积累规律;正确地处理测量成果,求出最可靠值;评定测量结果的精度;为选择合理的测量方法提供理论依据。
三、测量误差产生的原因1.测量仪器因素2.观测者的因素3.外界条件的因素测量观测条件——测量仪器、观测人员和外界条件这三方面的因素综合起来称为测量观测条件。
等精度观测——测量观测条件相同的各次观测称为等精度观测。
非等精度观测——测量观测条件不相同的各次观测称为非等精度观测。
四、测量误差的分类1.系统误差在相同的观测条件下对某量作一系列观测,如果误差的大小、符号表现出系统性,或按一定的规律变化,或保持不变,这种误差称为系统误差。
其特点:具有累积性,但可以采用适当的观测方法或加改正数来消除或减弱其影响。
2.偶然误差在相同的观测条件下对某量作一系列观测,如果误差的大小和符号不定,表面上没有规律性,但实际上服从于一定的统计规律性,这种误差称为偶然误差。
偶然误差单个的出现上没有规律性,不能采用适当的观测方法或加改正数来消除或减弱其影响。
因此,观测结果中偶然误差占据了主要地位,是偶然误差影响了观测结果的精确性。
五、减少测量误差的措施对系统误差,通常采用适当的观测方法或加改正数来消除或减弱其影响。
对偶然误差,通常采用多余观测来减少误差,提高观测成果的质量。
§5.2 偶然误差的特性一、精度的含义1.准确度准确度是指在对某一个量的多次观测中,观测值对该量真值的偏离程度。
2.精密度精密度是指在对某一个量的多次观测中,各观测值之间的离散程度。
3.精度精度也就是精确度,是评价观测成果优劣的准确度与精密度的总称,表示测量结果中系统误差与偶然误差的综合影响的程度。

第五章 测量误差的基本知识一、本章重点1.测量误差概念。
2.算术平均值原理。
3.评定观测值的精度标准二、本章难点1.观测值中误差及算术平均值中误差的概念。
2.偶然误差及特性。
3.观测值函数中误差的概念及其应用。
三、课时分配第一节 概 述在测量工作中,对某量(如某一个角度、某一段距离或某两点间的高差等)进行多次观测,所得的各次观测结果总是存在着差异,这种差异实质上表现为每次测量所得的观测值与该量的真值之间的差值,这种差值称为测量误差,即:测量误差 = 真值 - 观测值观测误差按其性质可分为两类: 1.系统误差在相同的观测条件下,对某量进行一系列的观测,若观测误差的符号及大小保持不变,或按一定的规律变化,这种误差称为系统误差。
这种误差往往随着观测次数的增加而逐渐积累。
如某钢尺的注记长度为30 m ,经鉴定后,它的实际长度为30.016 m ,即每量一整尺,就比实际长度量小0.016 m ,也就是每量一整尺段就有 + 0.016 m 的系统误差。
这种误差的数值和符号是固定的,误差的大小与距离成正比,若丈量了五个整尺段,则长度误差为5 ⨯ (+ 0.016) = + 0.080 m 。
若用此钢尺丈量结果为167.213 m ,则实际长度为:167.213 + 30213.167 ⨯ 0.0016 = 167.213 + 0.089 = 167.302 (m)由此可见,系统误差对观测结果影响较大,因此必须采用各种方法加以消除或减少它的影响。
比如用改正数计算公式对丈量结果进行改正。
再例如,角度测量时经纬仪的视准轴不垂直于横轴而产生的视准轴误差,水准尺刻划不精确所引起的读数误差,以及由于观测者照准目标时,总是习惯于偏向中央某一侧而使观测结果带有误差等都属于系统误差。
系统误差除可用改正数计算公式对观测结果进行改正加以消除外,也可以用一定的观测方法来消除其误差影响。
如经纬仪视准轴不垂直于横轴造成的误差,可以用盘左、盘右观测角度,取其平均值的方法加以消除;在水准测量中,采用前、后视距离相等来消除水准仪的视准轴不平行于水准管轴造成的误差。
第五章测量误差基本知识一、名词解释观测误差系统误差偶然误差误差传播定律二、填空题1.测量误差产生的原因、、;2.观测误差按误差的性质划分,可分为、、;3.评定观测值精度的标准有、、;三、选择题()1.下列误差为偶然误差的是A 钢尺尺长不准的量距误差B 水准仪的i角对读数的影响误差C 经纬仪的水准管轴不垂直于竖轴对读数的影响误差D 经纬仪度盘读数的估读误差E 水准尺未立竖直(倾斜)对仪器读数的影响误差F 经纬仪照准目标时的照准误差G 水准仪在水准尺上读数时最后一位数值的估读误差H 钢尺量距时尺子零点对准地面点位的对点误差()2.下列哪些量是评定观测值精度的标准A极限误差B中误差C相对误差D允许误差()3.地面上两点间的距离,用钢尺反复丈量,观测值中误差的计算公式为ABC D无法计算四、简答题1、简述偶然误差的四个特性五、计算题1.用钢尺反复丈量地面上A、B两点间的水平距离,观测数据如下:L1=124.365L5=124.368L2=124.372L6=124.361L3=124.370L7=124.366L4=124.367L8=124.368计算这组观测值的中误差、算术平均值的中误差和相对误差。
2.用经纬仪反复观测某一角度,得如下一组角度值β1=28°15′32″β2=28°15′28″β3=28°15′37″β4=28°15′46″β5=28°15′38″β6=28°15′40″试求这组观测值的中误差及算术平均值的中误差。
3.一测站水准测量,后视读数为 1.659m,前视读数为2.163m,水准仪在水准尺上的读数误差均为±2mm,求这一测站的高差及其中误差。
4.如图所示,从已知水准点A到B点进行水准测量,共测了4站,每一站水准仪的读数误差均为±2mm,A点的高程中误差为±8mm,试求B点的中误差。
5.水准仪在水准尺上的读数中误差为±2mm,求:⑴双仪器高法一测站高差中误差⑵三四等水准测量一测站高差中误差6.从已知水准点A到B点进行水准测量,水准仪的读数中误差为±2mm,A点的高程中误差为±8mm;要求B点的中误差不能超过±15mm,试求从A点到B点最多能测多少站?7.求DJ6经纬仪的一测回测角中误差,半测回测角中误差。