Bi_(1.5+x)Zn_1.0Nb_1.5 O_(7+1.5x)(x=0.075,0.15)陶瓷的结构和介电性能
- 格式:pdf
- 大小:278.36 KB
- 文档页数:4

经济数学基础课后答案(概率统计第三分册)完整的答案习题一1.写出下列事件的样本空间: (1) 把一枚硬币抛掷一次; (2) 把一枚硬币连续抛掷两次; (3) 掷一枚硬币,直到首次出现正面为止; (4) 一个库房在某一个时刻的库存量(假定最大容量为 M).解 (1) ={正面,反面} △{正,反} (2) ={(正、正),(正、反),(反、正),(反、反)} (3) ={(正),(反,正),(反,反,正),…} (4) ={x;0 ≤x≤ m}.2.掷一颗骰子的试验,观察其出现的点数,事件 A=“偶数点”, B=“奇数点”,C=“点数小于5”,D=“小于 5 的偶数点”,讨论上述各事件间的关系. = { ,2,3,4,5,6}, A = {2,4,6}, B = { ,3,5}, C = { ,2,3,4}, D = {2,4}. 1 1 1 解 A 与 B 为对立事件,即 B= A ;B 与 D 互不相容;A ? D,C ? D.3.事件 Ai 表示某个生产单位第 i 车间完成生产任务,i=1,2,3,B 表示至少有两个车间完成生产任务,C 表示最多只有两个车间完成生产任务,说明事件 B 及 B-C 的含义,并且用 Ai(i=1,2,3)表示出来.解 B 表示最多有一个车间完成生产任务,即至少有两个车间没有完成生产任务. B-C 表示三个车间都完成生产任务4.如图 1-1,事件 A、B、C A+B+C,AC+B,C-AB 用解 A + B = A + AB 图 1-1 B = A1 A2 + A2 A3 + A1 A3 B = A1 A2 A3+A1 A2 A3+A1 A2 A3+A1 A2 A3 C = A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 都相容,即ABC≠Φ,把事件 A+B,一些互不相容事件的和表示出来. A + B + C = A + AB + A BC B ? C = A1 A2 A3 AC + B = B + ABC 5.两个事件互不相容与两个事件对立的区别何在,举例说明.解两个对立的事件一定互不相容,它们不可能同时发生,也不可能同时不发生;两个互不相容的事件不一定是对立事件,它们只是不可能同时发生,但不一定同时不发生.在本书第 6 页例 2 中 A 与 D 是对立事件,与 D 是互不相容事 C 件.6.三个事件 A、B、C 的积是不可能事件,即 ABC=Φ,问这三个事件是否一定互不相容?画图说明.解不一定. A、B、C 三个事件互不相容是指它们中任何两个事件均互不相容,即两两互不相容.如图 1-2,事件 ABC=Φ,但是 A 与 B 相容. AB,D=A+B,F=A-B.说明事7.事件 A 与 B 相容,记 C=图 1-2 件 A、C、D、F 的关系.C ? AB = A BC + ABC + ABC 2 解由于 AB ? A ? A+B, A-B ? A ? A+B,与 A-B 互不相容, A=AB+(A-B).因 AB 且此有 A=C+F,C 与 F 互不相容,8.袋内装有 5 个白球,3 个黑球,从中一次任取两个,求取到的两个球颜色不同的概率.解记事件 A 表示“取到的两个球颜色不同”.则有利于事件A 的样本点数目 2 #A= C51C31 .而组成试验的样本点总数为#Ω= C5+3 ,由古典概率公式有 D ? A ? F,A ? C. P(A)= # A = #? 1 1 C5C3 15 = C82 28(其中#A,Ω 分别表示有利于 A 的样本点数目与样本空间的样本点总数,#余下同)9.计算上题中取到的两个球中有黑球的概率.解设事件 B 表示“取到的两个球中有黑球”则有利于事件 B 的样本点数为# B = C52 . P( B) = 1-P( B) = 1 ? C52 9 = 2 C8 1410.抛掷一枚硬币,连续 3 次,求既有正面又有反面出现的概率.“三次中既有正面又有反面出现” 则 A 表示三次均为正面或 , 解设事件 A 表示三次均为反面出现.而抛掷三次硬币共有 8 种不同的等可能结果,即#Ω=8,因此 P ( A) = 1 ? P( A) = 1 ? #A 2 3 = 1? = #? 8 411. 10 把钥匙中有 3 把能打开一个门锁,今任取两把,求能打开门锁的概率.解设事件 A 表示“门锁能被打开” 则事件 A 发生就是取的两把钥匙都不能打.开门锁. P( A) = 1 ? P( A) = 1 ? C2 8 #A = 1- 7 = 2 #? C10 15 从 9 题-11 题解中可以看到,有些时候计算所求事件的对立事件概率比较方便. 12.一副扑克牌有 52 张,不放回抽样,每次一张,连续抽取 4 张,计算下列事件的概率: (1)四张花色各异; (2)四张中只有两种花色.解设事件 A 表示“四张花色各异” B 表示“四张中只有两种花色”.; # 4 1 1 1 1 = C52,A = C13C13C13C13, # 2 1 3 1 2 2 # B = C(C 2 C13C13+C13C13 ) 4 P( A) = P( B) = # A 134 = 4 = 0.105 # C52 # B 6 7436+6048 () = = 0 . 300 4 # C52 13.口袋内装有 2 个伍分、3 个贰分,5 个壹分的硬币共 10 枚,从中任取 5 枚, 3 解求总值超过壹角的概率.设事件 A 表示“取出的 5 枚硬币总值超过壹角”. # 1 = C 10 ,=C 2 C83+C 2 3 C5+C 32 C52 ) #A(C 3 1 2 5 #A 126 P( A)===0.5 # 25214.袋中有红、黄、黑色球各一个,每次任取一球,有放回地抽取三次,求下列事件的概率: A=“三次都是红球” △“全红” B=“全白” ,, C =“全黑” D=“无红” E=“无白” ,,, F=“无黑” G=“三次颜色全相同” ,, H=“颜色全不相同” I=“颜色不全相同”., 3 解#Ω=3 =27,#A=#B=#C=1,#D=#E=#F=23=8,#G=#A+#B+#C=3,#H=3!=6,#I=#Ω-#G=24 P ( A) = P ( B ) = P (C ) = P ( D) = P ( E ) = P ( F ) = 1 27 8 27 P(G ) = 3 1 6 2 24 8 = , P( H ) = = , P( I ) = = 27 9 27 9 27 9 15.一间宿舍内住有 6 位同学,求他们中有 4 个人的生日在同一个月份的概率.解设事件 A 表示“有 4 个人的生日在同一个月份”. 1 #Ω=126,#A= C64C12112 P( A) = # A 21780 ==0.0073 # 12 6 16.事件 A 与 B 互不相容,计算 P ( A + B) .解由于 A 与 B 互不相容,有 AB=Φ,P(AB)=0 17.证 P( A + B) = P( AB) = 1 ? P( AB) = 1.设事件 B ? A,求证P(B)≥P(A).∵B ? A ∴P(B-A)=P(B) - P(A) ∵P(B-A)≥0 ∴P(B)≥P(A) 18.已知 P(A)=a,P(B)=b,ab≠0 (b>0.3a), P(A-B)=0.7a,求 P(B+A),P(B-A),P( B + A ).解由于 A-B 与 AB 互不相容,且 A=(A-B)+AB,因此有 P(AB)=P(A)-P(A-B)=0.3a P(A+B)=P(A)+P(B)-P(AB)=0.7a +b P(B-A)=P(B)-P(AB)=b-0.3a P( B + A )=1-P(AB)=1-0.3a 19. 50 个产品中有 46 个合格品与 4 个废品,从中一次抽取三个,计算取到废品的概率.,则 A 表示没有取到废品,有利于事件 A 的样本解设事件 A 表示“取到废品” 4 3 点数目为# A = C46 ,因此 P(A)=1-P( A )=1- #A =1-C46 3 3 # C50 =0.2255 20.已知事件 B ? A,P(A)=lnb ≠ 0,P(B)=lna,求 a 的取值范围.解因 B ? A,故P(B)≥P(A),即lna≥lnb, ? a≥b,又因 P(A)>0,P(B)≤1,可得 b>1,a≤e,综上分析 a 的取值范围是: 1<b≤a≤e 21.设事件 A 与 B 的概率都大于 0,比较概率 P(A),P(AB), P(A+B),P(A)+P(B)的大小(用不等号把它们连接起来).解由于对任何事件 A,B,均有AB ? A ? A+B 且 P(A+B)=P(A)+P(B)-P(AB),P(AB)≥0,因此有P(AB)≤P(A)≤P(A+B)≤P(A)+P(B) 22.一个教室中有 100 名学生,求其中至少有一人的生日是在元旦的概率(设一年以 365 天计算).解设事件 A 表示“100 名学生的生日都不在元旦” ,则有利于 A 的样本点数目为# A = 3 6 4 1 0 0 ,而样本空间中样本点总数为#Ω=365100,所求概率为 P( A) = 1 ? P( A) = 1 ? #A 364100 = 1? #? 365100 = 0.2399 23.从5 副不同手套中任取 4 只手套,求其中至少有两只手套配成一副的概率.解设事件 A 表示“取出的四只手套至少有两只配成一副” ,则 A 表示“四只手套中任何两只均不能配成一副”. P ( A) = 1 1 1 1 # A C54C2C2C2C2 80 = = 4 # C10 210 24.某单位有 92%的职工订阅报纸,93%的人订阅杂志,在不订阅报纸的人中仍有 85%的职工订阅杂志,从单位中任找一名职工求下列事件的概率: (1)该职工至少订阅一种报纸或期刊; (2)该职工不订阅杂志,但是订阅报纸.解设事件 A 表示“任找的一名职工订阅报纸” B 表示“订阅杂志” ,,依题意 P(A)=0.92,P(B)=0.93,P(B| A )=0.85 P(A+B)=P(A)+P( A B)=P(A)+P( A )P(B| A ) =0.92+0.08×0.85=0.988 P(A B )=P(A+B)-P(B)=0.988-0.93=0.058 25.分析学生们的数学与外语两科考试成绩,抽查一名学生,记事件 A 表示数学成绩优秀,表示外语成绩优秀, P(A)=P(B)=0.4, (AB)=0.28, P(A| B 若 P 求 B),P(B|A),P(A+B).解P(A|B)= P( AB) = 0.28 = 0.7 P( B) 0 .4 P(B|A)= P( AB) = 0.7 P ( A) P ( A) = 1 ? P ( A) = 0.62 P(A+B)=P(A)+P(B)-P(AB)=0.52 26.设 A、B 是两个随机事件. 0<P(A)<1,0<P(B)<1, 5 P(A|B)+P( A | B )=1.求证 P(AB)=P(A)P(B).证∵P ( A| B )+P ( A | B )=1 且 P ( A|B )+P( A | B )=1 ∴P ( A|B )=P (A| B ) P ( AB ) P ( A B ) P ( A) ? P ( AB ) = = P( B) 1 ? P( B) P( B) P(AB)〔1-P(B)〕=P( B)〔P( A)-P( AB)〕整理可得 P(AB)=P( A) P( B) 27.设 A 与 B 独立,P( A)=0.4,P( A+B)=0.7,求概率 P (B).解 P( A+B)=P(A)+P( A B)=P( A)+P( A ) P( B) ?0.7=0.4+0.6P( B ) ? P( B )=0.5 28.设事件 A 与 B 的概率都大于 0,如果 A 与 B 独立,问它们是否互不相容,为什么? 解因 P ( A ),P ( B )均大于 0,又因 A 与 B 独立,因此 P ( AB )=P ( A ) P ( B )>0,故 A 与B 不可能互不相容. 29.某种电子元件的寿命在 1000 小时以上的概率为 0.8,求 3 个这种元件使用 1000 小时后,最多只坏了一个的概率.,解设事件 Ai 表示“使用 1000 小时后第 i 个元件没有坏” i=1,2,3,显然 A1,A2,A3 相互独立,事件 A 表示“三个元件中最多只坏了一个” 则 A=A1A2A3+ A1 A2A3+A1 A2 A3+A1A2 A3 ,,上面等式右边是四个两两互不相容事件的和,且 P(A1)=P(A2)=P(A3)=0.8 P( A)= [P( A1 )]3 + 3[P( A1 )]2 P( A1 ) =0.83+3×0.82×0.2 =0.896 30.加工某种零件,需经过三道工序,假定第一、二、三道工序的废品率分别为 0.3,0.2,0.2,并且任何一道工序是否出现废品与其他各道工序无关,求零件的合格率.解设事件 A 表示“任取一个零件为合格品” ,依题意 A 表示三道工序都合格. P(A)=(1-0.3)(1-0.2)(1-0.2)=0.448 31.某单位电话总机的占线率为 0.4,其中某车间分机的占线率为 0.3,假定二者独立,现在从外部打电话给该车间,求一次能打通的概率;第二次才能打通的概率以及第 m 次才能打通的概率(m 为任何正整数).解设事件 Ai 表示“第 i 次能打通” i=1,2,…,m,则, P(A1)=(1-0.4)(1-0.3)=0.42 P(A2)=0.58 × 0.42=0.2436 P(Am)=0.58m-1 × 0.42 32.一间宿舍中有 4 位同学的眼镜都放在书架上,去上课时,每人任取一副眼镜,求每个人都没有拿到自己眼镜的概率.解设 Ai 表示“第 i 人拿到自己眼镜”,i=1,2,3,4. P ( Ai )= 1 ,设事件 B 4 表示“每个人都没有拿到自己的眼镜”.显然 B 则表示“至少有一人拿到自己的眼镜”.且 B =A1+A2+A3+A4. P( B )=P(A1+A2+A3+A4) 4 =∑ p( Ai ) ? ∑ P( Ai Ai ) + ∑ P( Ai A j Ak ) ? P( A1 A2 A3A4 ) i =1 1≤i<j ≤ 4 1≤i<j<k ≤ 4 6 P(AiAj) = P(Ai)P(Aj|Ai) =1×1 = 4 3 1 (1 ≤ i<j ≤ 4) 12P(AiAjAk)=P(Ai)P(Aj|Ai)P(Ak|AiAj) = 1 × 1 × 1 = 1 (1≤i<j<k≤4)P(A1A2A3A4) =P(A1)P(A2|A1)P(A3|A1A2) ×P(A4|A1A2A3) 4 3 2 1 1 1 1 5 2 3 P ( B ) = 4 × ? C 4 × + C4 × ? = 4 12 24 24 8 3 P( B) = 1 ? P( B) = 8 4 3 2 24 = 1 × 1 × 1 ×1 = 1 24 33.在 1,2,…,3000 这 3000 个数中任取一个数,设 Am=“该数可以被 m 整除”,m=2,3,求概率 P(A2A3),P(A2+A3),P(A2-A3).解依题意 P(A2)= 1 ,P(A3)= 1 2 3 P(A2A3)=P(A6)= 1 6 P(A2+A3)=P(A2)+P(A3)-P(A2A3) =1+1?1 = 2 2 3 6 3 2 6 3 P(A2-A3)=P(A2)-P(A2A3)= 1 ? 1 = 134.甲、乙、丙三人进行投篮练习,每人一次,如果他们的命中率分别为 0.8,0.7,0.6,计算下列事件的概率: (1)只有一人投中; (2)最多有一人投中; (3)最少有一人投中.解设事件 A、B、C 分别表示“甲投中”“乙投中”“丙投中” 、、,显然 A、B、C 相互独立.设 Ai 表示“三人中有 i 人投中” i =0,1,2,3,依题意,, P( A0 ) = P( A B C ) = P( A) P( B ) P(C ) P ( A3 )=P ( ABC )=P ( A ) P ( B ) P ( C ) =0.8×0.7×0.6 = 0.336 P(A2)=P(AB C )+P(A B C)+P( A BC) =0.8×0.7×0.4+0.8×0.3×0.6+0.2×0.7×0.6 = 0.452 (1) P(A1)=1-P(A0)-P(A2)-P(A3) =1-0.024-0.452-0.336=0.188 (2) P(A0+A1)=P(A0)+P(A1)=0.024+0.188=0.212 (3) P(A+B+C)=P( A0 )=1-P (A0)=0.976 35.甲、乙二人轮流投篮,甲先开始,假定他们的命中率分别为 0.4 及 0.5,问谁先投中的概率较大,为什么? 解设事件A2n-1B2n 分别表示“甲在第 2n-1 次投中”与“乙在第 2n 次投中” ,显然A1,B2,A3,B4,…相互独立.设事件 A 表示“甲先投中”. P( A) = P( A1 ) + P( A1 B 2 A3 ) + P( A1 B 2 A3 B 4 A5 ) + … = 0.4+0.6 × 0.5 × 0.4+(0.6 × 0.5) 2 × 0.4+… = 0.2×0.3×0.4× = 0.024 7 = 计算得知 P(A)>0.5,P( A )<0.5,因此甲先投中的概率较大. 36.某高校新生中,北京考生占 30%,京外其他各地考生占 70%,已知在北京学生中,以英语为第一外语的占 80%,而京外学生以英语为第一外语的占 95%,今从全校新生中任选一名学生,求该生以英语为第一外语的概率.解设事件 A 表示“任选一名学生为北京考生” B 表示“任选一名学生,以英,语为第一外语”.依题意 P(A)=0.3,P( A )=0.7,P(B|A)=0.8,P(B| A )= 0.95.由全概率公式有 P(B)=P(A)P(B|A)+P( A )P(B| A ) =0.3×0.8+0.7×0.95=0.905 37. A 地为甲种疾病多发区,该地共有南、北、中三个行政小区,其人口比为 9 : 7 : 4,据统计资料,甲种疾病在该地三个小区内的发病率依次为4‰,2‰,5‰,求A 地的甲种疾病的发病率.解设事件 A1,A2,A3 分别表示从 A 地任选一名居民其为南、北、中行政小区,易见 A1,A2,A3 两两互不相容,其和为Ω.设事件 B 表示“任选一名居民其患有甲种疾病” ,依题意: P(A1)=0.45,P(A2)=0.35,P(A3)=0.2, P(B|A1)=0.004,P(B|A2)=0.002,P(B|A3)=0.005 3 =∑ P( Ai ) P( B | Ai ) i =1 0 .4 4 = 1 ? 0 .3 7 = 0.45 × 0.004 + 0.35 × 0.002 + 0.2 × 0.005 =0.0035 38.一个机床有三分之一的时间加工零件 A,其余时间加工零件 B,加工零件 A 时,停机的概率为 0.3,加工零件 B 时停机的概率为 0.4,求这个机床停机的概率.解设事件 A 表示“机床加工零件A” ,则 A 表示“机床加工零件B” ,设事件 B 表示“机床停工”. P ( B ) = P ( A ) P ( B | A) + P ( A ) P ( B | A) 1 2 = 0.3 × + 0.4 × = 0.37 3 3 39.有编号为Ⅰ、Ⅱ、Ⅲ的 3 个口袋,其中Ⅰ号袋内装有两个 1 号球,1 个 2 号球与 1 个 3 号球,Ⅱ号袋内装有两个 1 号球和 1 个 3 号球,Ⅲ号袋内装有 3 个 1 号球与两个 2 号球,现在先从Ⅰ号袋内随机地抽取一个球,放入与球上号数相同的口袋中,第二次从该口袋中任取一个球,计算第二次取到几号球的概率最大,为什么? 解设事件 Ai 表示“第一次取到 i 号球” Bi 表示第二次取到 i 号球,i=1,2,, 3.依题意,A1,A2,A3 构成一个完全事件组. P ( A1 ) = 1 1 , P ( A2 ) = P ( A3 ) = 2 4 1 1 , P ( B2 | A1 ) = P ( B3 | A1 ) = 2 4 1 1 , P ( B2 | A2 ) = P ( B3 | A2 ) = 2 4 1 1 1 , P ( B2 | A3 ) = , P ( B3 | A3 ) = 2 3 6 P ( B1 | A1 ) = P ( B1 | A2 ) = P ( B1 | A3 ) = 8 应用全概率公式P( B j ) = ∑ P( Ai ) P( B j | Ai ) 可以依次计算出 P( B1 ) = 1 , 3 i =1 2 P ( B2 ) = 13 11 , P( B3 ) = 48 48 .因此第二次取到 1 号球的概率最大.40.接 37 题,用一种检验方法,其效果是:对甲种疾病的漏查率为 5%(即一个甲种疾病患者,经此检验法未查出的概率为 5%);对无甲种疾病的人用此检验法误诊为甲种疾病患者的概率为 1%,在一次健康普查中,某人经此检验法查为患有甲种疾病,计算该人确实患有此病的概率.解设事件 A 表示“受检人患有甲种疾病” B 表示“受检人被查有甲种疾病” ,,由 37 题计算可知 P(A)=0.0035,应用贝叶斯公式 P( A | B) = P ( A) P ( B | A) P ( A) P ( B | A) + P ( A) P ( B | A) 0.0035 × 0.95 = 0.0035 × 0.95+0.9965 × 0.01 = 0.25 41.甲、乙、丙三个机床加工一批同一种零件,其各机床加工的零件数量之比为 5 : 3 : 2,各机床所加工的零件合格率,依次为 94%,90%,95%,现在从加工好的整批零件中检查出一个废品,判断它不是甲机床加工的概率.解设事件 A1,A2,A3 分别表示“受检零件为甲机床加工”“乙机床加工”“丙,,机床加工” B 表示“废品” ,,应用贝叶斯公式有 P( A1 | B) = P( A1 ) P( B | A1 ) i =1 ∑ P( Ai ) P( B | Ai ) = 3 0.5 × 0.06 3 = 0.5 × 0.06+0.3 × 0.1+0.2 × 0.05 7 4 P( A1 | B) = 1 ? P( A1 | B) = 7 42.某人外出可以乘坐飞机、火车、轮船、汽车 4 种交通工具,其概率分别为 5%, 15%,30%,50%,乘坐这几种交通工具能如期到达的概率依次为 100%, 70%,60%与 90%,已知该旅行者误期到达,求他是乘坐火车的概率.解设事件 A1,A2,A3,A4 分别表示外出人“乘坐飞机”“乘坐火车”“乘坐轮,,船”“乘坐汽车” B 表示“外出人如期到达”.,, P( A2 | B) = P( A2 ) P( B | A2 ) ∑ P( Ai ) P( B | Ai ) i =1 4 = 0.15 × 0.3 0.05 × 0 + 0.15 × 0.3 + 0.3 × 0.4 + 0.5 × 0.1 =0.20943.接 39 题,若第二次取到的是 1 号球,计算它恰好取自Ⅰ号袋的概率.解39 题计算知 P(B1)= 1 ,应用贝叶斯公式 2 1 1 × P( A1 ) P( B1 | A1 ) 2 2 1 P( A1 | B1 ) = = = 1 P( B1 ) 2 244.一箱产品 100 件,其次品个数从 0 到 2 是等可能的,开箱检验时,从中随机地抽取 10 件,如果发现有次品,则认为该箱产品不合要求而拒收,若已9 知该箱产品已通过验收,求其中确实没有次品的概率.解设事件 Ai 表示一箱中有 i 件次品,i=0, 1, 2. B 表示“抽取的 10 件中无次品” ,先计算P ( B ) 10 10 2 1 C99 C98 P ( B ) = ∑ P ( Ai ) P ( B | Ai ) = × (1 + 10 + 10 ) i =0 3 C100 C100 1 P( A0 | B) = = 0.37 3P ( B )45.设一条昆虫生产 n 个卵的概率为pn = λn n! e ?λ n=0, 1, 2, … 其中λ>0,又设一个虫卵能孵化为昆虫的概率等于 p(0<p<1).如果卵的孵化是相互独立的,问此虫的下一代有 k 条虫的概率是多少? 解设事件 An=“一个虫产下几个卵” n=0,1,2….BR=“该虫下一代有 k 条,虫” k=0,1,….依题意,P( An ) = pn = λn n! e ?λ 0 ? P( Bk | An ) = ? k k n?k ?Cn p q ∞ k>n 0≤k ≤n ∞ 其中 q=1-p.应用全概率公式有 P( Bk ) = ∑ P ( An ) P( Bk | An ) = ∑ P( An ) P( Bk | An ) n =0 n=k ∞ =∑ n=l n! λ ?λ e p k q n?k n! k !( n ? k ) ! n (λp ) k ?λ ∞ (λq) n? k e ∑ k! n= k (n ? k ) ! 由于∑ (λq) ∞ (λ q ) n ? k = e λq ,所以有n = k ( n ? k ) ! n ? k =0 ( n ? k ) ! = n?k ∑ ∞ P( Bk ) = ( λ p ) k ? λ λq ( λ p ) p ? λp e e = e k! k k = 0, 1, 2,L 10习题二 1.已知随机变量 X 服从 0-1 分布,并且P{X≤0}=0.2,求 X 的概率分布.解 X 只取 0 与 1 两个值, {X=0}=P{X≤0}-P{X<0}=0.2, {X =1}=1-P{X P P =0}=0.8.2.一箱产品 20 件,其中有 5 件优质品,不放回地抽取,每次一件,共抽取两次,求取到的优质品件数 X 的概率分布.解 X 可以取 0, 1, 2 三个值.由古典概型公式可知 C m C 2? m P { X = m } = 5 215 (m = 0, 1, 2) C20 依次计算得 X 的概率分布如下表所示: X P 0 21 38 1 15 38 2 2 383.上题中若采用重复抽取,其他条件不变,设抽取的两件产品中,优质品为 X 件,求随机变量 X 的概率分布.解 X 的取值仍是 0, 1, 2.每次抽取一件取到优质品的概率是 1/4,取到非优质品的概率是 3/4,且各次抽取结果互不影响,应用伯努利公式有 9 ?3? P{X = 0} = ? ? = 4 ? 16 ? 6 1 ? 1 ?? 3 ? P { X = 1 } = C 2 ? ?? ? = 4 ?? 4 ? 16 ? 1 ?1? P { X = 2 }= ? ? = 4 ? 16 ? 2 24.第 2 题中若改为重复抽取,每次一件,直到取得优质品为止,求抽取次数 X 的概率分布.解 X 可以取1, 2, …可列个值.且事件{X = n}表示抽取 n 次,前 n-1 次均未取到优质品且第 n 次取到优质品,其概率为 ? 3 ? ? 1 .因此 X 的概率分布为 ? ? n ?1 ?4? 4 1?3? P {X = n } = ? ? 4?4? n ?1 n = 1, 2, …5.盒内有 12 个乒乓球,其中 9 个是新球,3 个为旧球,采取不放回抽取,每次一个直到取得新球为止,求下列随机变量的概率分布.(1)抽取次数 X; (2)取到的旧球个数 Y .解 (1)X 可以取 1, 2, 3, 4 各值. 3 3 9 9 P { X =1 }= P {X = 2 } = × = 4 12 11 3 2 9 9 P { X = 3 }= × × = 12 11 10 220 44 11 P { X = 4 }= 3 2 1 9 1 × × × = 12 11 10 9 220 (2) Y 可以取 0, 1, 2, 3 各值. 3 P {Y = 0 }= P { X =1 }= 4 9 P {Y =1 }= P { X = 2 }= 44 9 P {Y = 2 }= P { X = 3 }= 220 1 P {Y = 3 }= P { X = 4 }= 2206.上题盒中球的组成不变,若一次取出 3 个,求取到的新球数目 X 的概率分布.解 X 可以取 0, 1, 2, 3 各值. C33 1 P {X = 0 } = 3 = C12 1 9 220P {X = 1 } = P {X = 2 } = P {X = 3 } = CC 27 = 3 C12 220 1 C92C3 108 = 3 220 C12 3 C9 84 = 3 C12 220 2 37.已知 P{X=n}=pn,n=1, 2, 3, …, 求 p 的值.∞ 解根据∑ P { X = n }=1 , 有n =1 1 = ∑ Pn = n=1 ∞ p 1? p 解上面关于 p 的方程,得 p =0.5. 8.已知 P{X=n}=pn, n=2, 4, 6, …,求 p 的值. 2 解 p2 + p4 + p6 + … = p 2 = 1 1? p 解方程,得p= ± 2 /29.已知 P{X=n}=cn, n=1, 2, …, 100, 求 c 的值.100 解 1 = ∑ cn = c ( 1 + 2 + … + 100 ) =5050 c n =1 解得 c=1/5050 .10.如果 pn=cn_2,n=1, 2, …, 问它是否能成为一个离散型概率分布,为什么? ∞ ∞ ∞ ∞ ∞ 解∑ pn = c ∑ 12 , 由于级数∑ 12 收敛, 若记∑ 12 =a,只要取 c = 1 , 则有∑ pn =1, 且 n =1 n=1 n n =1 n n =1 n a n =1 pn>0.所以它可以是一个离散型概率分布.11.随机变量 X 只取 1, 2, 3 共三个值,其取各个值的概率均大于零且不相等并又组成等差数列,求 X 的概率分布.解设 P{X=2}=a,P{X=1}=a-d, P{X=3}=a+d.由概率函数的和为 1,可知 a= 1 , 但是 a-d 与 a+d 均需大于零, 3 因此|d|< 1 , X 的概率分布为 3 X 1 2 3 12 P 1 -d 3 1 3 3 1 +d 3 其中 d 应满足条件:0<|d|< 1 12.已知 P { X 解∞ m =1 = m }= ∞ cλ ?λ ,m e m! m =1, 2, …, 且λ>0, 求常数 c. 1 = ∑ p{X = m} = ∑ ∞ cλm ?λ e m =1 m ! = eλ 由于∑ ∞ λm m =0 m ! = 1+ ∑ ∞ λm , 所以有 m =1 m !13.甲、乙二人轮流投篮,甲先开始,直到有一人投中为止,假定甲、乙二人投篮的命中率分别为 0.4 及 0.5,求: (1)二人投篮总次数 Z 的概率分布; (2)甲投篮次数 X 的概率分布; (3)乙投篮次数 Y 的概率分布.解设事件 Ai 表示在第 i 次投篮中甲投中,表示在第 j 次投篮中乙投中,=1, 3, j i 5, …, j=2, 4, 6,…,且 A1, B2, A3, B4,…相互独立. (1) P{Z = 2k ? 1} = p{A1 B1 L A 2 k ?3 B 2 k ?2 A2 k ?1 } = (0.6×0.5) k ?1 ·0.4 = 0.4(0.3) k ?1 k=1, 2, … P{Z = 2k } = p( A1 B1 L A2 k ?3 B 2 k ? 2 A2 k ?1 B2 k ) k = 0.5×0.6×(0.6×0.5) k ?1 =0.3 k=1, 2, … (2) P{X = n} = p{A1 B1 L A2 n?3 B 2n?2 A2 n?1 } + p A1 B1 L A 2 n ?3 B 2 n ?2 A2 n?1 B2 n = (0.6 × 0.5) n?1 (0.4 + 0.6 × 0.5) = 0.7 × 0.3n?1 n = 1, 2, K (3) P { Y = 0 } = P( A1 ) = 0.4 P { Y = n } = P A1 B1 K A 2 n?1 B2 n + P A1 B1 K A 2 n?1B 2 n A2 n+1 = (0.6 × 0.5) n?1 × 0.6 × (0.5 + 0.5 × 0.4) = 0.42 ×0.3n?1 n = 1, 2,K cλm ?λ ∑1 m ! e = c(e λ ? 1)e ?λ = c(1 ? e ?λ ) = 1 m= 1 解得c= 1 ? e ?λ { } { } { }14.一条公共汽车路线的两个站之间,有四个路口处设有信号灯,假定汽车经过每个路口时遇到绿灯可顺利通过,其概率为 0.6,遇到红灯或黄灯则停止前进,其概率为 0.4,求汽车开出站后,在第一次停车之前已通过的路口信号灯数目 X 的概率分布(不计其他因素停车).解 X 可以取 0, 1, 2, 3, 4 . P { X =0 } =0.4 P { X=1 }=0.6×0.4=0.24 2 P { X=2 } =0.6 ×0.4=0.144 P { X=3 } =0.63×0.4=0.0864 P { X=4 } =0.64=0.1296 15. ?sin x , f ( x) = ? ? 0, x ∈ [ a , b] ,其他. 13 问 f(x)是否为一个概率密度函数,为什么?如果(1) a = 0 , b = π ; (2) a = 0 , b = π ; (3) a = π , b = 3 π . 2 2 解π 在〔0, π 2 〕与〔0, π〕上,sinx≥0,但是∫ 0π sin xdx ≠ 1, ? π ? 上,sinx ? ? 3 2 ∫ 0 sin xd x = 1, 而在?π, ? 2 ≤0.因此只有(1)中的 a, b 可以使 f (x)是一个概率密度函数. 16. ?x ? x , ? e 2c f ( x) = ? c ? 0, ? 2 x>0 ,x ≤ 0.其中 c>0,问 f(x)是否为密度函数,为什么? 解易见对任何x∈(-∞ , +∞) , f ( x ) ≥ 0,又∫ +∞ 0 x ? 2c e dx = 1 c x2 f(x)是一个密度函数. 17.解 ?2 x , f ( x) = ? ? 0, a<x <a + 2.其他.问 f ( x )是否为密度函数,若是,确定 a 的值;若不是,说明理由.如果 f ( x )是密度函数,则 f ( x )≥0,因此a≥0,但是,当a≥0 时, 2 a +2 ∫ a 2 × dx = x | a = 4 a + 4 ≥ 4 a+2 由于∫+∞ f ?∞ ( x) dx 不是 1,因此 f ( x )不是密度函数.a < x<+ ∞ , 其他. 18.设随机变量 X~f ( x ) 2 ? , ? f ( x ) = ? π ( 1 + x2 ) ? 0, ? 确定常数 a 的值,如果 P { a < x < b } =0.5,求 b 的值.解+∞ 2 2 2 π dx = arctan x ∫ = ( ? arctan a) 2 a π (1 + x ) a π π 2 2 ?π ? 解方程 ? -arctana ? =1 π ?2 ? ∫ +∞ 得 a = 0 b P { 0 < x < b } = ∫0 f ( x ) dx = 2 2 arctan x |b = arctan b 0 π π 解关于 b 的方程:2 arctanb=0.5 π 得 b=1.19.某种电子元件的寿命 X 是随机变量,概率密度为 ?100 ? f ( x ) = ? x2 ? 0, ? x ≥ 100 , x<100 . 3 个这种元件串联在一个线路中,计算这 3 个元件使用了 150 小时后仍能使线路正常工作的概率. 14 解串联线路正常工作的充分必要条件是 3 个元件都能正常工作.而三个元件的寿命是三个相互独立同分布的随机变量,因此若用事件 A 表示“线路正常工作” ,则 P ( A ) = [ P ( X >150) ]3 2 + ∞ 100 P { X > 150 }=∫ 150 dx = 2 x 3 8 P( A)= 27 20.设随机变量 X~f ( x ),f ( x )=Ae-|x|,确定系数 A;计算 P { |X | ≤ 1 }.∞ 解 1 = ∫ ?+∞ Ae ? | x | dx = 2 A ∫ 0+∞ e ? x dx = 2 A 解得 A=1 2 1 ?1 1 1 ?| x| e dx = ∫ e ? x dx 0 2 P {| X | ≤1 }= ∫ 21.设随机变量 Y 服从〔0, 5〕上的均匀分布,求关于 x 的二次方程 4x2+4xY+Y+2=0 有实数根的概率.解 4x2+4xY+Y+2=0.有实根的充分必要条件是△=b2-4ac =16Y2-16(Y+2)=16Y2-16Y-32≥0 设事件 P(A)为所求概率.则P ( A) = P {16Y 2 ? 16Y ? 32 ≥ 0 } = P { Y ≥ 2 } + P { Y ≤ ?1 } =0.6 22.设随机变量 X ~ f ( x ), ? c , ? f ( x) = ? 1 ? x 2 ? 0, ? | x | <1,其他.= 1 ? e ?1 ≈ 0.632 确定常数 c,计算P ? | X | ≤ 1 ? .? ? ? 2? 解 1 = ∫?1 1 c 1? x 2 dx = c arcsin x |1 1 = cπ ? c =1 π 1? 1 2 dx = arcsin x ? = 21 2 ? ∫? 2 π 1 ? x 2 π 1 1 2 0 ? P ? | X |≤ ? = 1 3 23.设随机变量 X 的分布函数 F ( x )为 ? 0, ? F ( x) = ? A x , ? 1, ? x<0 , 0<x<1 , x ≥ 1.确定系数 A,计算P { 0 ≤ X ≤ 0.25 },求概率密度 f ( x ).解连续型随机变量 X 的分布函数是连续函数,F F (1-0),有 A=1. (1)= 15 ? 1 , ? f ( x ) = ?2 x ? 0, ? 0<x<1 , 其他. P { 0 ≤ X ≤ 0.25 } = F ( 0.25 ) ? F ( 0 ) = 0.5 24.求第 20 题中 X 的分布函数 F ( x ) .解 F ( x ) = P { X ≤ x } = ∫ ?x∞ 1 e ? | t | dt 2 当t ≤ 0 时, F ( x ) = ∫ ?∞ x 1 t 1 e dt = e x 2 2 当 t>0 时, x 1 01 x1 F ( x ) = ∫ ?∞ e ? | t | dt = ∫ ?∞ e ?t dt + ∫0 e -t dt2 22 1 1 1 ?x ?x = + (1 ? e ) = 1 ? e 2 2 2 25.函数(1+x2)-1 可否为连续型随机变量的分布函数,为什么? 解不能是分布函数,因 F (-∞)= 1 ≠ 0.a ,确定 a 的值;求分布函数 26.随机变量 X ~ f ( x ),并且 f ( x ) = 2 π (1+ x ) F ( x );计算 P { | X | <1 } .解 1 = ∫ ?∞ +∞ a a ∞ dx = arctan x +∞ = a ? π ( 1+ x2 ) π 因此a =1 F ( x) = ∫ ?∞ x 1 1 dt= arctan t ?x∞ 2 π ( 1+ t ) π 1 1 = + arctan x 2 π 1 1 1 1 P { | X | <1 } = ∫ ?1 dx = 2 ∫ 0 dx 2 π ( 1+ x ) π ( 1+ x2 ) 2 1 = arctan x 01 = π 2 27.随机变量 X 的分布函数 F ( x ) 为: A ? , ?1 ? F ( x) = ? x 2 ? 0, ? x>2 ,x ≤ 2.确定常数 A 的值,计算P { 0 ≤ X ≤ 4 } .解由 F ( 2+0 )=F ( 2 ),可得1? A =0, 4 A=4 P { 0 ≤ X ≤ 4 } = P { 0<X ≤ 4 } = F ( 4 ) ? F ( 0 ) = 0.75 f 28.随机变量 X~f ( x ), ( x )= A , 确定 A e x + e?x 的值;求分布函数 F ( x ) . 16 解 1 = ∫ ?∞ 因此A ex ∞ dx = A ∫ ? ∞ dx e x + e ?x 1 + e2x π = A arctan e x ∞∞ = A ? 2 A= 2 ,π ∞ ?∞ F (x)=∫ 2 2 dt = arctan et π ( et + e ?t ) π 2 = arctan e x π x x ?∞ 29.随机变量 X~f ( x ), ? 2x ? , 0<x <a f ( x ) = ? π2 ? 0 , 其他.其他 ? 确定 a 的值并求分布函数 F ( x ) .解1 = ∫0 a 2x x2 dx = 2 2 π π a 0 = a2 π2 因此,a = π 当 0<x<π 时,F ( x ) ∫0 2t x2 dt = 2 π2 π ?0, x ≤ 0 ? 2 ?x F ( x) = ? 2 , x<π 0<?π ?1, x ≥ π ? x 30.随机变量 X 的分布函数为 ?0 , ? F ( x ) = ? a 2 x 2 + 2ax + 2 ?ax e , ?1 ? 2 ? x≤0 x>0 (a>0) 求 X 的概率密度并计算 P ? 0<X< 1 ? . ? ? ? a ? 解当x ≤0 时,X 的概率密度 f ( x ) =0;当 x > 0 时,f ( x ) =F′ ( x ) ? 0, ?f ( x ) = ? a 3 x 2 ?ax e , ? ? 2 x≤0, 0. x> 31.随机变量 X 服从参数为 0.7 的 0-1 分布,求 X2,X2-2X 的概率分布.解 X2 仍服从 0-1 分布,且 P { X2=0 } =P { X=0 } =0.3,P{X2=1}=P{X 1 ? 1 ? 1 ? ? P ? 0<x< ? = P ? 0<x ≤ ? = F ( ) ? F ( 0 ) a ? a ? a ? ? 5 ?1 = 1 ? e ≈ 0.08 2 17 =1}=0.7 X2-2X 的取值为-1 与 0 , P{X2-2X=0} =P { X =0 } =0.3 P { X2-2X=-1 } =1-P { X=0 } =0.7 32.已知 P { X=10n } =P { X=10-n }= 1n , n = 1 , 2 , K , 解 Y=lgX,求 Y 的概率分布. Y 的取值为±1, ±2 , … P { Y=n } =P { lgX=n } =P { X=10n } = 1 3 3 3 P { Y=-n } =P { lgX=-n } =P { x=10-n } = 1 n=1 , 2 , … 33. X 服从〔a , b〕上的均匀分布,Y=ax+b (a≠0),求证 Y 也服从均匀分布.证设Y 的概率密度为 fY ( y ) ,X 的概率密度为 fX ( x ),只要 a ≠ 0, y = ax + b 都是 x 的单调函数.当 a > 0 时,Y 的取值为〔a2+b , ab+b〕, x=h( y)= 1 1 ( y ? b ) , h′ ( y ) = x ′ = y a a 1 f Y ( y ) = h′ ( y ) f X [ h ( y ) ] = , y ∈ [ a 2 + b , ab + b ], a (b?a ) 当y ∈ [ a 2 + b , ab + b ] 时, fY ( y ) =0.类似地,若 a<0,则 Y 的取值为〔 ab+b ,a2+b 〕? ?1 , ? f Y ( y) = ? a(b ? a) ? 0, ? ab + b ≤ y ≤ a 2 + b , 其他.因此,无论 a>0 还是 a<0,ax+b 均服从均匀分布. 34.随机变量 X 服从〔0 , π 2 〕上的均匀分布 Y=cosX , 求 Y 的概率密度 fY ( y ).解 y=cosx 在〔0, h′ ( y ) = ?1 1? y 2 π 2 〕上单调,在(0 , 1)上,h ( y ) = x =arccosy 2 π , fx ( x ) = 0< y <1 , 其他., 0 ≤ x ≤ π 2 .因此 2 ? , ? fY ( y ) = ? π 1 ? y 2 ? 0, ? 35.随机变量 X 服从(0 , 1)上的均匀分布,Y=ex , Z =|lnX|,分别求随机变量 Y 与 Z 的概率密度 fY ( y ) 及 fZ ( z ) .解 y = ex 在(0 , 1)内单调 , x=lny 可导,且x′y = 1 , fX ( x ) =1 y 0 < x < 1 , 因此有 18 ?1 ? , fY ( y ) ? y ? 0, ? 1< y < e , 其他.在(0 , 1)内 lnx < 0|lnx|=-lnx 单调,且 x = e ? z ,x′z=-e ? z ,因此有 ?e ? z , fz ( z ) = ? ? 0, 0 < z <+ ∞, 其他. 36.随机变量 X~f ( x ) , ?e ? x , f (x)=? ? 0, x>0 x≤0 Y = X , Z = X2 , 分别计算随机变量 Y 与 Z 的概率密度 fy ( y ) 与 fZ ( z ) .解当 x > 0 时,y = x 单调,其反函数为x = y2 , x′y = 2y ?2 y e ? y , ? fY ( y ) = ? ? 0, ? 2 y>0 , y ≤ 0. z 当 x > 0 时 z=x2 也是单调函数,其反函数为 x = ? 1 ? e ? f z ( z) = ? 2 z ? 0, ? z , x′ z= 1 2 z z>0 ,z ≤ 0. (x)= 2 37.随机变量 X~f ( x ),当x ≥ 0 时, f π (1 + x 2 ) , Y=arctanX , Z = 解 1 X ,分别计算随机变量 Y 与 Z 的概率密度 fY ( y ) 与 fz ( z ) . ? 2? 其反函数x=tany , x′ y=sec2y 在? ? 0, π ? 内由于 y = arctanx 是单调函数,? ? π 2 2 f Y ( y ) = sec y = π (1 + tan 2 y ) π 即 Y 服从区间(0 , π )上的均匀分布. 2 1 z = 在 x>0 时也是 x 的单调函数,其反函数 x= 1 x z 2 恒不为零,因此,当 0 < y < 2 时,, x′ z = ?1 . 2 z 因此当 z>0 时,fz ( z ) = ?1 2 2 = 2 z π [ 1+ ( 1 )2 ] π ( 1 + z 2 ) z 2 ? , z>0 ? f z ( z ) = ? π(1 + z 2 ) ? 0, z≤0 ? 19 即Z = 圆心在原点的圆的上半圆周上随机游动.求该质点横 38.一个质点在半径为 R,坐标 X 的密度函数 fX ( x ) .解如图,设质点在圆周位置为 M,弧 M A 的长记为 L,显然 L 是一个连续型随机变量,L 服从〔0,πR〕上的均匀分布.?1 , ? f L ( l ) = ? πR ? 0, ? 0 ≤ l ≤ πR ,其他. 1 X 与 X 同分布.M 点的横坐标 X 也是一个数,且图 2-1 随机变量,它是弧长 L 的函 X =Rcosθ = Rcos 函数 x = Rcosl / R 是 l 的单调函数 ( 0< l <πR ) ,其反函数为 l =Rarccos x R ′ lx = ?R R2 ? x2 L R 当-R < x < R 时,L′x ≠ 0,此时有fX ( x ) = ?R R ?x 2 2 ? 1 1 = πR π R 2 ? x 2 当 x ≤ -R 或x ≥ R 时,fX ( x ) =0 . 39.计算第 2 ,3 , 5 , 6 , 11 各题中的随机变量的期望.解根据第 2 题中所求出的 X 概率分布,有EX = 0 × 21 15 2 1 + 1× + 2 × = 38 38 38 2 亦可从 X 服从超几何分布,直接计算EX = n N1 5 1 = 2× = N 20 2 + 1× 6 1 1 + 2× = 16 16 16 2 1 亦可从 X 服从二项分布(2, ),直接用期望公式计算:4 1 1 EX = np = 2 × = 4 2 9 9 1 + 3× + 4× = 1 .3 4 44 220 220 (2) EY = 0 × 3 +1 × 9 + 2 × 9 + 3 × 1 = 0.3 4 44 220 220 1 27 在第 6 题中,EX = 0 × +1 × + 2 × 108 + 3 × 84 = 2.25 220 220 220 220 1 ?1 ? ?1 ? 在第 11 题中, EX = 1 × ? ?d ? + 2 × + 3 × ? + d ? 3 ?3 ? ?3 ? 在第 3 题中EX = 0 × 9 在第 5 题中(1) EX = 1 × 3 + 2 × 20 = 2 + 2d 0<|d|< 1 3 40. P { X = n } = c , n=1, 2, 3, 4, 5, 确定 C 的值并计算 EX.解n c c c c c 137c =1 ∑ =c+ + + + = n =1 n 2 3 4 5 60 5 C= 60 137 5 n =1 EX = ∑ n ? 41.随机变量X 只取-1, 0, 1 三个值,且相应概率的比为 1 : 2 : 3,计算 EX.解设 P { X =-1 } = a,则 P { X =0 } =2a, P { X=1 } =3a ( a>0 ) ,因 a + 2a + 3a = 1 , 故 a =1/6 EX = ?1 × c 300 = 5C = n 137 42.随机变量 X 服从参数为 0.8 的 0-1 分布,通过计算说明 EX2 是否等于 ( EX )2 ? 解 EX =P { X=1 } =0.8,( EX )2 =0.64 EX2=1×0.8=0.8>( EX )2 43.随机变量 X~f ( x ) ,f ( x ) =0.5e- | x |,计算 EXn,n 为正整数.解当 n 为奇数时,x n f EX n = ∫ ?∞ 0.5x ne ? | x | dx = 0 +∞ 1 2 3 1 + 0 × + 1× = 6 6 6 3 ( x ) 是奇函数,且积分∫ 0 x n e ? x dx 收敛,因此∞ 当 n 为偶数时,EX n = ∫ ?∞ 0.5x n e ? | x | dx = 2∫ 0 0.5x n e ? x dx = ∫0 +∞ +∞ +∞ x n e ? x dx = Γ ( n + 1 ) = n ! 44.随机变量 X~f ( x ) ,? x, ? f ( x) = ?2 ? x , ? 0, ? n 0 ≤ x ≤1, 1<x <2 , 其他.其他计算 EX (n 为正整数) .解EX n = ∫ ?∞ x n f ( x )dx = ∫ 0 x n+1dx + ∫ 1 ( 2 ? x ) x n dx 1 2 +∞ = 1 2 1 + ( 2 n+1 ?1 ) ? (2 n+ 2 ) ? 1 n + 2 n +1 n+2 2 n+2 ? 2 = ( n +1) ( n + 2 ) 45.随机变量 X~f ( x ) ,?cx b , f (x)=? ? 0, 0 ≤ x ≤1, 其他.其他 c =1 b +1 b,c 均大于 0,问 EX 可否等于 1,为什么? 解而EX = ∫ 0 cx b +1dx = 1 b ∫ ?∞ f ( x )dx = ∫ 0 cx dx = 1 +∞ c b+2 21 由于方程组 ? c ?b + 1 = 1 ? ? ? c =1 ?b + 2 ? 无解,因此 EX 不能等于 1. 46.计算第 6,40 各题中 X 的方差 DX .解在第 6 题中,从第 39 题计算知 EX= 9 , 4 27 4 × 108 9 × 84 1215 EX = + + = 220 220 220 220 2 DX=EX2-( EX )2≈0.46 在第 40 题中,已计算出 EX=300 , 137 c 5 EX 2 = ∑ n 2 × = ∑ cn = 15c n =1 n n=1 900 = 137 5 DX=EX2-(EX)2≈1.77 47.计算第 23,29 各题中随机变量的期望和方差.解在第 23 题中,由于 f ( x ) = 1 (0<x<1),因此2 x 1 1 EX = ∫ 0 dx = 3 2 x 2 x 1 1 EX 2 = ∫ 0 dx = 5 2 x x DX = EX2-( EX )2 =4 45 π 在第 29 题中,由于 f ( x ) = 2x ( 0<x<π ) , 因此2 EX = ∫ 0 2x 2 dx = π 2 π 3 2x3 π2 π EX 2 = ∫ 0 2 dx =π 2 π 2 2 DX=EX2-( EX )2= π 解∞ EY= ∫ ?+∞ yfY ( y ) dy = ∫ 01 2 18 dy = 2 π 48.计算第 34 题中随机变量 Y 的期望和方差.2y π 1? y 2 EY2= ∫ 01 2 2y π 1? y2 dy = 1 2 DY= 1 ? 4 π2 ? 8 = π2 2π 2 49.已知随机变量 X 的分布函数 F ( x ) 为: 22 F ( x ) 0, ? ? 2 ?1 + x + x , 2 = ?2 ? 2 ? 1 + x- x , ?2 2 ? 1, ? x< ? 1,? 1 ≤ x<0 ,0 ≤ x <1,x ≥ 1.计算 EX 与 DX .解依题意,X 的密度函数 f ( x ) 为: ?1 + x , ? f ( x ) = ?1 ? x , ? 0,? ? 1 ≤ x<0 ,0 ≤ x<1,其他.解EX=∫ ?01 x ( 1 + x ) dx + ∫ ?01 x ( 1 ? x ) dx = 0 EX2= ∫ ?01 x 2 ( 1 + x ) dx + ∫ 01 x 2 ( 1 ? x ) dx = 1 DX= 16 6 50.已知随机变量 X 的期望 EX=μ,方差 DX=σ2,随机变量 Y = 和 DY .解 EY = 1 ( EX-μ ) =0 σ X ?? σ , 求EY DY = DX σ2 =1 1 ) 4 51.随机变量 Yn~B ( n, 并画出概率函数图. ,分别就 n=1, 2, 4, 8, 列出 Yn 的概率分布表,解 Y1 P Y3 P Y4 P 0 3 4 1 1 4 Y2 P 1 27 64 0 9 16 1 6 16 2 1 16 0 27 64 2 9 64 3 1 64 0 81 256 1 108 256 2 54 256 3 12 256 4 1 256 Y8 0 1 2 3 4 5 6 78 23 P 6561 1749 2041 1360 5670 1512 252 24 a a 6a 2a 8a a a a a 其中a = 1/65536 .图略. 52.设每次试验的成功率为 0.8,重复试验 4 次,失败次数记为 X,求 X 的概率分布.解 X 可以取值 0, 1, 2, 3, 4 .相应概率为 P ( X=m ) =C44?m × 0.84?m × 0.2m ( m=0, 1, 2, 3, 4 ) 计算结果列于下表 X P 0 1 2 3 4 0.4096 0.4096 0.1536 0.0256 0.0016 53.设每次投篮的命中率为 0.7,求投篮 10 次恰有 3 次命中的概率;至少命中 3 次的概率.解记 X 为 10 次投篮中命中的次数,则 X~B ( 10 , 0.7 ) . 3 P { X = 3 } = C10 0.7 3 0.37 ≈ 0.009 P { X ≥ 3 }= 1? P { X = 0 }? P { X = 1 }? P { X = 2 } =1-0.310-10×0.7×0.39-45×0.72×0.38 ≈0.9984 54.掷四颗骰子,求“6 点”出现的平均次数及“6 点”出现的最可能(即概率最大)次数及相应概率.解掷四颗骰子,记“6 点”出现次数为 X,则 X~B(4, 1 ).6 EX = np =2 3 55.已知随机变量 X~B(n, p),并且 EX=3,DX=2,写出 X 的全部可能取值,并计算P { X ≤ 8 } .解根据二项分布的期望与方差公式,有 ?np = 3 ? ?npq = 2 5 ,其 X 的最可能值为〔 6 5 625 P { X = 0 } = ( )4 = 6 1296 500 若计算 P { X = 1 } = ,显然 P { x = 2 } , P { x = 3 } , 1296 P { x = 4 } 概率更小.由于 np + p = np + p 〕=0 解方程,得q= 2 ,p= 1 ,n=9 . 3 3 X 的全部可能取值为0, 1, 2, 3, …, 9 .P { X ≤ 8 }= 1? P { X = 9 } = 1-( 1 ) 9 ≈ 0.9999 56.随机变量 X~B(n,p)EX=0.8,EX2=1.28,问 X 取什么值的概率最大,其,概率值为何? 解由于 DX = EX2-(EX)2=0.64, EX=0.8, 即 3 24 ?npq = 0.64 ? ?np = 0.8 解得 q = 0.8,p = 0.2,n = 4 .由于 np+p=1,因此 X 取 0 与取 1 的概率最大,其概率值为 P { X = 0 } = P { X = 1 } = 0.8 4 = 0.4096 57.随机变量 X~B(n, p)Y=eaX,计算随机变量 Y 的期望 EY 和方差 DY .,解随机变量 Y 是 X 的函数,由于 X 是离散型随机变量,因此 Y 也是离散型随机变量,根据随机变量函数的期望公式,有i EY = ∑ e ai P{X = i}∑ e ai C n p i q n?i = i=0 n i =0 n n ∑ C (e p ) q = i =0 i n a i n i =0 n?i = (e a p + q ) n EY 2 = ∑ (e ai ) 2 P{X = i} i ∑ C n (e 2 a p) i q n ?i = (e 2 a p + q) n = i =0 n DY = (e 2 ap + q) n ? (e ap + q ) 2 n 58.从一副扑克牌(52 张)中每次抽取一张,连续抽取四次,随机变量 X,Y 分别表示采用不放回抽样及有放回抽样取到的黑花色张数,分别求 X,Y 的概率分布以及期望和方差.解 X 服从超几何分布,Y 服从二项分布 B(4, 1 ).2 P {X = m} = C C C m 26 4?m 26 4 52 1 1 (m = 0,1,2,3,4) P{Y = m} C 4m ( ) m ( ) 4?m (m = 0,1,2,3,4) = 2 2 具体计算结果列于下面两个表中. X P Y P EX = n 0 1 2 3 4 46/833 208/833 325/833 208/833 46/833 1 4/16 2 6/16 3 4/16 4 1/16 0 1/16 59.随机变量 X 服从参数为 2 的泊松分布,查表写出概率 P{X = m}m = 0,1,2,3,4 并与 , 上题中的概率分布进行比较.X N1 26 = 4× =2 N 52 N N N ?n 26 26 48 16 DX = n 1 ? 2 ? = 4× × × = N N N ?1 52 52 51 17 1 EY = np = 4 × = 2 DY = npq = 1 2 P 0 1 2 3 4 0.1353 0.2707 0.2707 0.1804 0.0902 60.从废品率是 0.001 的 100000 件产品中,一次随机抽取 500 件,求废品率不超过 0.01 的概率.解设 500 件中废品件数为X,它是一个随机变量且 X 服从 N=100000, N1 =100, n=500 的超几何分布.由于 n 相对于 N 较小,因此它可以用二项分布 B 500,( 0.001)近似.又因在二项分布 B(500,0.001)中,n=500 比较大,而 p=0.001 非常小, 25 因此该二项分布又可用泊松分布近似,其分布参数λ=np=0.5.? X P? ≤ 0.001 } = P{X ≤ 5} ? 500 5 0 .5 m e ?0.5 = 0.999986 ≈ ∑ m = 0 m! 61.某种产品每件表面上的疵点数服从泊松分布,平均每件上有 0.8 个疵点,若规定疵点数不超过 1 个为一等品,价值 10 元;疵点数大于 1 不多于 4 为二等品,价值 8 元;4 个以上者为废品,求:(1)产品的废品率;(2)产品价值的平均值解设 X 为一件产品表面上的疵点数目,(1) P{X>4}= 1 ? P{X ≤ 3}= 1 ? ∑ P{X = m} 0.0014 = m=0 3 (2)设一件产品的产值为 Y 元,它可以取值为 0,8,10.EY = 0 × P{Y = 0} 8 × P{Y = 8} 10 × P{Y = 10} + + 1 } = 8P{<X ≤ 4} 10 P{X ≤ 1 + = 8 × 0.1898 + 10 × 0.8088 ≈ 9.61(元) 62.设书籍中每页的印刷错误服从泊松分布,经统计发现在某本书上,有一个印刷错误的页数与有 2 个印刷错误的页数相同,求任意检验 4 页,每页上都没有印刷错误的概率.解设一页书上印刷错误为X ,4 页中没有印刷错误的页数为 Y ,依题意, P{X = 1 = P{X = 2}}即λe ? λ = λ22! e ?λ 解得λ=2,即 X 服从λ=2 的泊松分布. p = P{X = 0} e ?2 = 显然 Y~B (4, e ?2 ) 63.每个粮仓内老鼠数目服从泊松分布,若已知一个粮仓内,有一只老鼠的概率为有两只老鼠概率的两倍,求粮仓内无鼠的概率.解设 X 为粮仓内老鼠数目,依题意 P{X = 1 = 2 P{X = 2}}P{Y = 4}p 4 = e ?8 = λe ? λ = 2 × λ2 2! e ?λ 解得λ=1. P{X = 0} e ?1 = 64.上题中条件不变,求 10 个粮仓中有老鼠的粮仓不超过两个的概率.解接上题,设 10 个粮仓中有老鼠的粮仓数目为 Y,则 Y~B(10,p),其中 P = X>0} 1 ? P{X = 0} 1 ? e ?1 , q = e ?1 { = = P{Y ≤ 2}= P{ Y = 0} P{ Y = 1 + P{ Y = 2} + } = e ?8 (36e ?2 ? 80e ?1 + 45) ,65.设随机变量 X 服从 [2, 3] 上的均匀分布,计算 E(2X),D(2X) D(2 X )2 . 26 解 1 76 , EX 2 = DX + ( EX ) 2 = 12 12 1 E(2X)=5,D(2X)=4DX= ,3 2 2 2 D (2 X ) = D (4 X ) = 16 DX = 16 EX 4 ? ( EX 2 ) 2 211 3 EX 4 = ∫ 2 x 4 dx =5 211 5776 1504 DX 2 = EX 4 ? ( EX 2 ) 2 = ? = 5 144 720 1504 D (2 X ) 2 = 16 DX 2 = 45 EX=2.5,DX= [ ] 66.随机变量 X 服从标准正态分布,求概率P X ≤ 3} P 2.35 ≤ X ≤ 5}P X ≤ 1}P X ≤ ?7}., { ,{ , {{解P X ≤ 3}= Φ (3) = 0.9987 { P 2.35 ≤ X ≤ 5 = Φ (5) ? Φ (2.35) = 0.0094 {}P X ≤ 1 = Φ (1) = 0.8413 {}P X ≤ ?7 = 1 ? Φ (7) = 0 {} 67.随机变量 X 服从标准正态分布,确定下列各概率等式中的 a 的数值: = (2)P{ X ≤ a} = 0.9; (1) P{X ≤ a} 0.9; ;(3)P{X ≤ a} = 0.97725; (4)P{ X ≤ a} = 0.1; 解(1)P { X ≤ a} = Φ (a) = 0.9 ,查表得 a=1.28 (2)P { X ≤ a} = 2Φ (a ) ? 1 = 0.9 ,得Φ(a)=0.95,查表得 a=1.64 (3)P { X ≤ a} = Φ (a) = 0.97725 ,查表得 a =2 (4)P{ X ≤ a} = 2Φ(a) ? 1 = 0.1 ,得Φ (a)= 0.55,查表得 a = 0.13 68.随机变量 X 服从正态分布 N (5,2 2 ) ,求概率 P{5<X <8}, P{X ≤ 0} , P{ X ? 5 <2}.解 ?8?5? ?5?5? P{5<X<8} = Φ ? ? ?Φ ? ? ?2 ? ? 2 ? = Φ (1.5) ? Φ (0) = 0.4332 P {X ≤ 0} = Φ (? 2.5) = 1 ? Φ (2.5) = 0.0062 ? X ?5 ? P{ X ? 5 <2} = P ? ≤ 1? = 2Φ (1) ? 1 2 ? ? =0.6826 69.随机变量 X 服从正态分布N ( ? ,σ 2 ) ,若 P{X<9} = 0.975 , P{X<2} = 0.062 ,计算μ 和σ 的值,求 P{X>6}. ?9?? ? 解 P{X<9} = Φ ? ? = 0.975 ? σ ? ?2?? ? ? ? ?2? P{X<2} = Φ? ? = 0.062, Φ? ? = 0.938 ? σ ? ? σ ? 查表得:27 ?9 ? ? ? σ = 1.96 ? ? ? ? ? 2 = 1.54 ? σ ? 解以μ 和σ 为未知量的方程组,得μ =5.08,σ=2. P{X>6} = 1 ? P{X ≤ 6} = 1 ? Φ (0.46) =0.3228 70.已知随机变量 X~N (10,2 2 ) , P{X ? 10<c} = 0.95 , P{X<d} = 0.023 ,确定 c 和 d 的值.? X ? 10 c ? P{ X ?10 <c} = P ? <? 2? ? 2 = 2Φ ? c ? ? 1 = 0.95 ? ? ?2? ?c? Φ ? ? = 0.975 , ?2? 查表得 c = 1.96, c = 3.92 2 ? d ? 10 ? P{X<d} = Φ ? ? = 0.023 ? 2 ? 解 ? 10 ? d ? ? = 0.977 ? 2 ? 查表得 ? 10 ? d ? = 2, d = 6 ? ? ?2 ? Φ? 71.假定随机变量 X 服从正态分布N ( ? ,σ 2 ) ,确定下列各概率等式中 a 的数值:(1)P{? ? aσ<X<? + aσ } = 0.9; (2)P{? ? aσ<X<? + aσ } = 0.95; (3) P{? ? aσ<X<? + aσ } = 0.99; 解 ? X ?? ? P{? ? aσ<X<? + aσ } = P ? <a ? ? σ ? =2Φ(a) -1 (1)2Φ (a)-1=0.9,Φ (a)=0.95,a=1.64;(2)2Φ (a)-1=0.95,Φ (a)=0.975, a=1.96;(3)2Φ (a)-1=0.99,Φ (a)=0.995,a=2.58. 72.某科统考的考试成绩 X 近似服从正态分布 N (70, 10 2 ) , 第 100 名的成绩为 60 分,问第 20 名的成绩约为多少分? 解P{X ≥ 60} ≈ 1 ? P{X ≤ 60} = 1 ? Φ ? 60 ? 70 ? ? ? ?10 ? = Φ (1) = 0.8413.设参加统考人数为 n,则 100 =0.8413,n= 100 ≈ 19 n 0.8413 设第 20 名成绩约为 a 分,则P{X ≥ a} = 20 ≈ 0.1681 n 28 P{X ≤ a} = 0.8319 ? a ? 70 ? ? = 0.8319 ? 10 ? 查表得 a ? 70 = 0.96 10。

最新苏科版七年级上学期期中学业质量监测试题(满分:150分 考试时间:120分钟)题号一二三总分积分人 核分 人1-89-18 19 20 21 22 23 24 25 26 27 28 得分一、选择题(每小题3分,共24分.把正确的答案前的字母填入下表相应的空格)1.下列结论正确的是A .34-的倒数是43 B .13-的相反数是13C .33--=D .以上结论都不对 2.下列各数:30%,0,-2,431,π2-,∙1.2,0.2002000200002……,3.1415926,-3.141414……中,有理数的个数是A .9个B .8个C .7个D .6个 3.下列等式中,不成立的是A .3322-= B .22(2)2-= C .33(2)2-=- D .44(2)2-=-题号 1 2 3 4 5 6 7 8答案4.如果()2210a b ++-=,那么代数式(a +b)2014的值是A .-2014B .2014C .-1D .15.为计算简便..,把(-2.4)-(-4.7)-(+0.5)+(+3.4)+(-3.5)写成省略加号的和的形式,并按要求交换加数的位置正确的是A . -2.4+3.4-4.7-0.5-3.5B . -2.4+3.4+4.7+0.5-3.5C . -2.4+3.4+4.7-0.5-3.5D . -2.4+3.4+4.7-0.5+3.56.小明买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x 张,根据题意,下面所列方程正确的是A .x +5(12-x )=48B .x +5(x -12)=48C .x +12(x -5)=48D .5x +5(12-x )=487.七年级同学进行体能测试,一班有a 个学生,平均成绩m 分,二班有b 个学生,平均成绩n 分,则一、二班所有学生的平均成绩为 A .b a n m ++ B .2n m + C .b a nb ma ++ D .n m nbma ++8.若有理数a 满足2a a a -=,则a 的取值范围是 A .0a > B .0a < C .0a ≥ D .0a ≤二、填空题(每小题3分,共30分.把答案填在下面的横线上)9.一天早晨的气温是-7℃,中午上升了11℃,晚上又下降了9℃,晚上的气温是 ▲ .9. 10. 11. 12. 13. 14. 15. 16. 17. 18.10.关于x 的方程(k -3)x 2+2x -3=0是一元一次方程,则k =_____▲____. 11.若代数式m b a 32-与413b a n +的和是单项式,则2m+3n = ▲ .12. 已知地球的表面积约为510000000平方千米,数510000000用科学计数法可表示为▲_.13.平方等于25的数是__▲___14. 已知有理数在数轴上的位置如图所示,则式子2a c a b a ---+的化简结果是_▲_. 15.已知m 、n 互为相反数,p 、q 互为倒数,且a 为最大的负整数时,则20152014m npq a +++ 的值为 ▲ .16.已知x -2y =-4,则代数式(2y -x)2-2x +4y -1的值为___▲___. 17.定义运算a ⊗b =a(1-b),下面给出了关于这种运算的四个结论:①2⊗(-2)=6 ②a ⊗b =b ⊗a③若a +b =0,则(a ⊗a)+(b ⊗b)=2ab ④若a ⊗b =0,则a =0. 其中正确结论的序号是 ▲ (填上你认为所有正确结论的序号).18.观察下面图形,若将一个正方形平均分成2n 个小正方形,则一条直线最多..可穿过 ▲ 个小正方形.三、解答题(本大题共8题,共96分.解答应写出必要的文字说明、证明过程或演算步骤)19.(本题满分20分)计算:(1)(-1.25)+3.75+(+3.875)+(-314)+1.25+(-378)2n =3n =4n =第18题图c ba第14题图得分评卷人(2)()53112246⎛⎫+-⨯- ⎪⎝⎭(3)(-44.65)× 234+(-34.15)×(-234)+10.5 ×(-734) (4)42232[5(3)]()(18)92-÷--+-⨯-20.解下列方程(每小题5分,共10分) (1)223123x x +--= (2)1.5 1.50.50.63x x--=得分评卷人21.(本题满分10分)小虫从某点O 出发在一直线上来回爬行,若假定向右爬行的路程记为正数,向左爬行的路程记为负数,已知小虫爬行的路程依次记为:+5,-3,+10,-8,-6,+12,-10(单位:厘米),则: (1)小虫最后回到出发点O 了吗?若没有,在点O 的什么地方?(2)在爬行过程中,如果爬1厘米奖励两粒芝麻,则小虫一共得到多少粒芝麻?22.(本题满分10分)先化简,再求值:已知代数式A =2x 2+4xy +2y -1,B =x 2-xy +x -12. (1)当x =y =-2时,求A -2B 的值; (2)若A -2B 的值与x 的取值无关,求y 的值.23.(本题满分10分)魔术师为大家表演魔术. 他请观众想一个数,然后将这个数按以下得分评卷人得分评卷人得分评卷人步骤操作:魔术师立刻说出观众想的那个数.(1)如果小明想的数是-2那么他告诉魔术师的结果应该是 ;(2)如果小聪想了一个数并告诉魔术师结果为90,那么魔术师立刻说出小聪想的那个数 是 ;(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,请你说出其中的奥妙. 24.(本题满分10分)如图,用3个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个长方形ABCD ,若GH=2cm , GK=2cm , 设BF=x cm .(1)用含x 的代数式表示CM= cm ,DM= cm.; (2)若DC=10cm ,求x 的值;(3)求长方形ABCD 的周长(用x 的代数式表示),并求x=3时长方形周长.乘以3 减去3除以3加上6告诉魔术师结果ABCDE G FM K H ① ①① ②②③④得分评卷人25.(本题满分12分)观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…(1)请根据你发现的规律填空:6×8+1= ; (2)用含n 的等式表示上面的规律: ; (3)用找到的规律解决下面的问题: 计算: 1111(1)(1)(1)(1)13243520132015+++⋅⋅⋅+⨯⨯⨯⨯ 26.(本题满分14分)已知数轴上有A 、B 、C 三个点,分别表示有理数-24,-10,10,动点P 从A 出发,以每秒1个单位的速度向终点C 移动,设移动时间为t 秒.(1)用含t 的代数式表示P 到点A 和点C 的距离:PA= ,PC= ; (2)当点P 运动到B 点时,点Q 从A 点出发,以每秒3个单位的速度向C 点运动,Q 点得分评卷人得分评卷人到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.531(12)(12)(12)24630(9)237=-⨯+-⨯--⨯=-+-+=-17( 1.25)(3)(3.75 1.25)( 3.875)(3)484.5500.5⎡⎤⎡⎤=-+-+++++-⎢⎥⎢⎥⎣⎦⎣⎦=-++=原式七年级数学参考答案一、选择题(本大共8题,共24分)二、填空题(本大共10题,共30分)9. -5; 10. 3; 11. 14 ; 12. 85.110⨯; 13.5±; 14. -c -b ; 15. 2014; 16. 23 ; 17. ①③; 18. 2n-1.三、解答题(本大共8题,共96分)19.(1)解:……………4分……………5分(2)解:原式 ……………2分……………4分……………5分(3)解:原式=(43.65)×(-234)+(-34.15)×(-234)+10.5×(-234) ……1分 =(43.65+10.5-34.15)×(-234) ……………3分题 号 1 2 3 4 5 6 7 8 答 案BCDDCACD=20×(-234)……………4分=-55 ……………5分(4)解:原式= -16÷4+(-4+27)…………………3分= -4+23 ……………………4分=19 ……………………5分20.解:(1)4 9x=;…………………………………………………………4分(2)6 17x=.……………………………………………………………8分21.解(1)+5+(-3)+10+(-8)+(-6)+12+(-10)=0,回到O点………………………4分(2)2×(5+3+10+8+6+12+10)=108 ………………………10分22. 解:(1)A﹣2B=2x2+4xy+2y﹣1﹣2()=2x2+4xy+2y﹣1﹣2x2+2xy﹣2x+1=6xy+2y﹣2x,当x=y=﹣2时,A﹣2B=6xy+2y﹣2x=6×(﹣2)×(﹣2)+2×(﹣2)﹣2×(﹣2)=24; (5)分(2)由(1)可知A﹣2B=6xy+2y﹣2x=(6y﹣2)x+2y,若A﹣2B的值与x的取值无关,则6y﹣2=0,解得13y=. (10)分23.解:(1)3; (2)分(2)85; (5)分(3)设他们所想的数为x,则魔术师的结果为3363x-+,即x+5,故魔术师的结果减5即得到答案 (10)分24. 解:(1)CM=2+x;DM= 2+2x ……………………4分(2)x=2;……………………7分(3)16x+16 ……………………9分当x=3时,16x+16=16×3+16=64 ……………………10分25. 解:(1)49;……………………2分(2)2(2)1(1)n n n ++=+. ……………………6分 (3)原式=131241351201220141201320151()()()...()()1324352012201420132015⨯+⨯+⨯+⨯+⨯+⨯⨯⨯⨯⨯⨯⨯⨯⨯ ……8分 =2222223420132014 (1324352012201420132015)⨯⨯⨯⨯⨯⨯⨯⨯⨯ ……………………10分 =40282015……………………12分26. 解:(1)PA=t ,PC=34﹣t …………………4分(2)当P 点在Q 点右侧,且Q 点还没有追上P 点时,3t+2=14+t 解得:t=6,∴此时点P 表示的数为﹣4, …………………6分 当P 点在Q 点左侧,且Q 点追上P 点后,相距2个单位,3t ﹣2=14+t 解得:t=8, ∴此时点P 表示的数为﹣2, …………………8分当Q点到达C点后,当P点在Q点左侧时,14+t+2+3t﹣34=34解得:t=13,∴此时点P表示的数为3, (10)分当Q点到达C点后,当P点在Q点右侧时,14+t﹣2+3t﹣34=34解得:t=14,∴此时点P表示的数为4, (12)分综上所述:点P表示的数为﹣4,﹣2,3,4. (14)分。

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
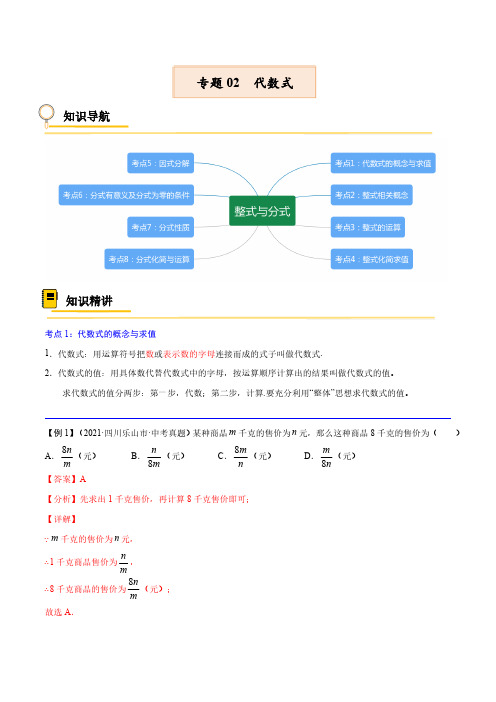
考点1:代数式的概念与求值1.代数式:用运算符号把数或表示数的字母连接而成的式子叫做代数式.2.代数式的值:用具体数代替代数式中的字母,按运算顺序计算出的结果叫做代数式的值。
求代数式的值分两步:第一步,代数;第二步,计算.要充分利用“整体”思想求代数式的值。
【例1】(2021·四川乐山市·中考真题)某种商品m 千克的售价为n 元,那么这种商品8千克的售价为( )A .8n m (元)B .8n m (元)C .8m n (元)D .8m n(元)【答案】A【分析】先求出1千克售价,再计算8千克售价即可;【详解】∵m 千克的售价为n 元,∴1千克商品售价为n m,∴8千克商品的售价为8n m (元);故选A.专题02 代数式【例2】(2021·内蒙古中考真题)若1x =+,则代数式222x x -+的值为( )A .7B .4C .3D.3-【答案】C 【分析】先将代数式222x x -+变形为()211x -+,再代入即可求解.【详解】解:())22222=111113x x x -+-+=+-+=.故选:C【例3】(2021·贵州铜仁市·中考真题)观察下列各项:112,124,138,1416,…,则第n 项是______________.【答案】12nn +【分析】根据已知可得出规律:第一项:1111122=+,第二项:2112242=+,第三项:3113382=+…即可得出结果.【详解】解:根据题意可知:第一项:1111122=+,第二项:2112242=+,第三项:3113382=+,第四项:41144162=+,…则第n 项是12n n +;故答案为:12n n +.有关代数式的常见题型为用代数式表示数字或图形的变化规律. 数与图形的规律探索问题,关键要能够通过观察、分析、联想与归纳找出数或图形的变化规律,并用代数式表示出来.1.(2021·浙江金华市·中考真题)某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是()A.先打九五折,再打九五折B.先提价50%,再打六折C.先提价30%,再降价30%D.先提价25%,再降价25%【答案】B【分析】设原件为x元,根据调价方案逐一计算后,比较大小判断即可.【详解】设原件为x元,∵先打九五折,再打九五折,∴调价后的价格为0.95x×0.95=0.9025x元,∵先提价50%,再打六折,∴调价后的价格为1.5x×0.6=0.90x元,∵先提价30%,再降价30%,∴调价后的价格为1.3x×0.7=0.91x元,∵先提价25%,再降价25%,∴调价后的价格为1.25x×0.75=0.9375x元,∵0.90x<0.9025x<0.91x<0.9375x故选B2.(2021·四川达州市·中考真题)如图是一个运算程序示意图,若开始输入x的值为3,则输出y值为___________.【答案】2【分析】根据运算程序的要求,将x=3代入计算可求解.【详解】解:∵x =3<4∴把x =3代入1(4)y x x =-£,解得:312y =-=,∴y 值为2,故答案为:2.3.(2021·湖南常德市·中考真题)如图中的三个图形都是边长为1的小正方形组成的网格,其中第一个图形有11´个正方形,所有线段的和为4,第二个图形有22´个小正方形,所有线段的和为12,第三个图形有33´个小正方形,所有线段的和为24,按此规律,则第n 个网格所有线段的和为____________.(用含n 的代数式表示)【答案】2n 2+2n【分析】本题要通过第1、2、3和4个图案找出普遍规律,进而得出第n 个图案的规律为S n =4n +2n ×(n -1),得出结论即可.【详解】解:观察图形可知:第1个图案由1个小正方形组成,共用的木条根数141221,S =´=´´第2个图案由4个小正方形组成,共用的木条根数262232,S =´=´´第3个图案由9个小正方形组成,共用的木条根数383243,S =´=´´第4个图案由16个小正方形组成,共用的木条根数4104254,S =´=´´…由此发现规律是:第n 个图案由n 2个小正方形组成,共用的木条根数()22122,n S n n n n =+=+g 故答案为:2n 2+2n .考点2:整式相关概念1.单项式:只含有数字与字母的积的代数式叫做单项式.单独的一个数或一个字母也是单项式.2.多项式:几个单项式的和叫做多项式. 多项式中次数最高的项的次数,叫做这个多项式的次数.3.整式:单项式与多项式统称整式.4.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.【例4】(2021·青海中考真题)已知单项式4272m a b -+与223m n a b +是同类项,则m n +=______.【答案】3【分析】根据同类项的定义(所含字母相同,相同字母的指数相同),求出m ,n 的值,再代入代数式计算即可.【详解】解:∵单项式4272m a b -+与223m n a b +是同类项,∴2m =4,n +2=-2m +7,解得:m =2,n =1,则m +n =2+1=3.故答案是:3.【例5】(2021·云南中考真题)按一定规律排列的单项式:23456,4,9,16,25a a a a a ,……,第n 个单项式是( )A .21n n a +B .21n n a -C .1n n n a +D .()21n n a +【答案】A【分析】根据题目中的单项式可以发现数字因数是从1开始的正整数的平方,字母的指数从1开始依次加1,然后即可写出第n 个单项式,本题得以解决.【详解】解:∵一列单项式:23456,4,9,16,25a a a a a ,...,∴第n 个单项式为21n n a +,故选:A .【例6】已知(m ﹣3)x 3y |m |+1是关于x ,y 的七次单项式,求m 2﹣2m +2= .【答案】17【分析】直接利用单项式的次数确定方法分析得出答案.【详解】解:∵(m ﹣3)x 3y |m |+1是关于x ,y 的七次单项式,∴3+|m |+1=7且m ﹣3≠0,解得:m =﹣3,∴m 2﹣2m +2=9+6+2=17.故答案为:17.1.①单项式中的数字因数称为这个单项式的系数;②一个单项式中,所有字母的指数的和叫做这个单项式的次数2.几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数1.(2021·上海中考真题)下列单项式中,23a b 的同类项是()A .32a b B .232a b C .2a b D .3ab 【答案】B【分析】比较对应字母的指数,分别相等就是同类项【详解】∵a 的指数是3,b 的指数是2,与23a b 中a 的指数是2,b 的指数是3不一致,∴32a b 不是23a b 的同类项,不符合题意;∵a 的指数是2,b 的指数是3,与23a b 中a 的指数是2,b 的指数是3一致,∴232a b 是23a b 的同类项,符合题意;∵a 的指数是2,b 的指数是1,与23a b 中a 的指数是2,b 的指数是3不一致,∴2a b 不是23a b 的同类项,不符合题意;∵a 的指数是1,b 的指数是3,与23a b 中a 的指数是2,b 的指数是3不一致,∴3ab 不是23a b 的同类项,不符合题意;故选B2.关于多项式5x 4y ﹣3x 2y +4xy ﹣2,下列说法正确的是( )A .三次项系数为3B .常数项是﹣2C .多项式的项是5x 4y ,3x 2y ,4xy ,﹣2D .这个多项式是四次四项式【答案】B【分析】根据多项式的项、次数的定义逐个判断即可.【详解】解:A 、多项式5x 4y ﹣3x 2y +4xy ﹣2的三次项的系数为﹣3,错误,故本选项不符合题意;B 、多项式5x 4y ﹣3x 2y +4xy ﹣2的常数项是﹣2,正确,故本选项符合题意;C 、多项式5x 4y ﹣3x 2y +4xy ﹣2的项为5x 4y ,﹣3x 2y ,4xy ,﹣2,错误,故本选项不符合题意;D 、多项式5x 4y ﹣3x 2y +4xy ﹣2是5次四项式,错误,故本选项不符合题意;故选:B .3.若单项式﹣x 3y n +5的系数是m ,次数是9,则m +n 的值为 .【答案】0【分析】先依据单项式的系数和次数的定义确定出m 、n 的值,然后求解即可.【解答】解:根据题意得:m =﹣1,3+n +5=9,解得:m =﹣1,n =1,则m +n =﹣1+1=0.故答案为:0.考点3:整式的运算1.幂的运算性质:(1)同底数幂相乘底数不变,指数相加. 即:a m ·a n =a m +n (m ,n 都是整数).(2)幂的乘方底数不变,指数相乘. 即:(a m )n =a mn (m ,n 都是整数).(3)积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘. 即:(ab )n =a n b n (n 为整数).(4)同底数幂相除底数不变,指数相减. 即:a m ÷a n =a m -n (a ≠0,m,n 都为整数).(5)a 0=1(a ≠0), a -n =a1 (a ≠0).2.整式的运算:(1)整式的加减:几个整式相加减,如果有括号就先去括号,再合并同类项.(2)整式的乘法:单项式与单项式相乘,把它们的系数、相同字母分别相乘;单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加,即m (a +b +c )=ma +mb +mc ;多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加,即(m +n )(a +b )=ma +mb +na +nb .(3)整式的除法:单项式除以单项式,把系数与同底数幂分别相除,作为商的因式;多项式除以单项式,先把这个多项式的每一项分别除以这个单项式,再把所得的商相加.3.乘法公式:(1)平方差公式:(a +b )(a -b )=a 2-b 2.(2)完全平方公式:(a ±b )2=a 2±2ab +b 2.(3)常用恒等变换:a 2+b 2=(a +b )2-2ab=(a -b )2+2ab ;(a -b )2=(a +b )2-4ab.【例7】(2021·河南中考真题)下列运算正确的是()A .22()a a -=-B .2222a a -=C .23a a a ×=D .22(1)1a a -=-【答案】C【分析】直接利用幂的运算性质和完全平方公式分别判断得出答案.【详解】解:A 、22()a a -=,原计算错误,不符合题意;B 、2222a a a -=,原计算错误,不符合题意;C 、23a a a ×=,正确,符合题意;D 、22(1)21a a a -=-+,原计算错误,不符合题意;故选:C .【例8】(2021·福建中考真题)下列运算正确的是()A .22a a -=B .()2211a a -=-C .632a a a ¸=D .326(2)4a a =【答案】D【分析】根据不同的运算法则或公式逐项加以计算,即可选出正确答案.解:A :()221a a a a -=-=,故 A 错误;B :()22121a a a -=-+,故 B 错误;C :63633a a a a -¸==,故C 错误;D :()()2232332622·44a a a a ´===.故选:D【例9】(2021·江苏连云港市·中考真题)下列运算正确的是()A .325a b ab+=B .22523a b -=C .277a a a +=D .()22112x x x -+-=【答案】D【分析】根据同类项与合并同类项、全完平方差公式的展开即可得出答案.【详解】解:A ,3a 与2b 不是同类项,不能合并,故选项错误,不符合题意;B ,25a 与22b 不是同类项,不能合并得到常数值,故选项错误,不符合题意;C ,合并同类项后2787a a a a +=¹,故选项错误,不符合题意;D ,完全平方公式:()22211221x x x x x =-++-=-,故选项正确,符合题意;故选:D .1.(2021·浙江丽水市·中考真题)计算:()24a a -×的结果是()A .8a B .6a C .8a -D .6a -【答案】B 【分析】根据乘方的意义消去负号,然后利用同底数幂的乘法计算即可.【详解】解:原式24246a a a a +=×==.2.(2021·四川宜宾市·中考真题)下列运算正确的是( )A .23a a a +=B .()32622a a =C .623a a a ¸=D .325a a a ×=【答案】D【分析】根据同底数幂相乘底数不变指数相加、同底数幂相除底数不变指数相减、乘积的幂等于各部分幂的乘积运算法则求解即可.【详解】解:选项A :a 与2a 不是同类项,不能相加,故选项A 错误;选项B :()32628a a =,故选项B 错误;选项C :62624a a a a -¸==,故选项C 错误;选项D :33522a a a a +×==,故选项D 正确;故选:D .3.(2021·黑龙江齐齐哈尔市·中考真题)下列计算正确的是()A .B .C .D .【答案】A【分析】根据平方根,幂的乘方与积的乘方,单项式乘以单项式及合并同类项的运算法则分别对每一个选项进行分析,即可得出答案.【详解】A 、,正确,故该选项符合题意;B 、,错误,故该选项不合题意;C 、,错误,故该选项不合题意;D 、与不是同类项,不能合并,故该选项不合题意;故选:A .考点4:整式化简求值【例10】(2021·湖南永州市·中考真题)先化简,再求值:,其中.【分析】先计算完全平方公式、平方差公式,再计算整式的加减法,然后将代入求值即可得.4=±()2234636m n m n =24833a a a ×=33xy x y -=4=±()2234639m n m n =24633a a a ×=3xy 3x ()()212(2)x x x +++-1x =1x =【详解】解:原式,,将代入得:原式.1.(2021·四川南充市·中考真题)先化简,再求值:,其中.【分析】利用平方差公式和完全平方公式,进行化简,再代入求值,即可求解.【详解】解:原式===,当x =-1时,原式==-22.2.(2020•凉山州)化简求值:(2x +3)(2x ﹣3)﹣(x +2)2+4(x +3),其中x=【分析】先利用平方差公式、完全平方公式、单项式乘多项式法则展开,再去括号、合并同类项即可化简原式,继而将x 的值代入计算可得答案.【详解】原式=4x 2﹣9﹣(x 2+4x +4)+4x +12=4x 2﹣9﹣x 2﹣4x ﹣4+4x +12=3x 2﹣1,当x原式=3×2﹣1=3×2﹣1=6﹣1=5.考点5:因式分解因式分解的步骤:(概括为“一提,二套,三检查”)(1)先运用提公因式法:ma +mb +mc =m (a +b +c ).(2)再套公式:a 2-b 2=(a +b )(a -b ),a 2±2ab +b 2=(a ±b )2(乘法公式的逆运算).(3)最后检查:分解因式是否彻底,要求必须分解到每一个多项式都不能再分解为止.22214x x x =+++-25x =+1x =2157=´+=2(21)(21)(23)x x x +---1x =-2241(4129)x x x ---+22414129x x x --+-1210x -()12110´--【例11】(2021·广西贺州市·中考真题)多项式32242x x x -+因式分解为( )A .()221x x -B .()221x x +C .()221x x -D .()221x x +【答案】A 【分析】先提取公因式2x ,再利用完全平方公式将括号里的式子进行因式分解即可【详解】解:32242x x x -+()()2222121x x x x x =-+=-故答案选:A .【例12】(2021·浙江杭州市·中考真题)因式分解:214y -=( )A .()()1212y y -+B .()()22y y -+C .()()122y y -+D .()()212y y -+【答案】A 【分析】利用平方差公式因式分解即可.【详解】解:214y -=()()1212y y -+,故选:A .【例13】(2020•成都)已知a =7﹣3b ,则代数式a 2+6ab +9b 2的值为 .【答案】49【分析】先根据完全平方公式变形,再代入,即可求出答案.【详解】∵a =7﹣3b ,∴a +3b =7,∴a 2+6ab +9b 2=(a +3b )2=72=49,故答案为:49.本考点是中考的高频考点,其题型一般为填空题,难度中等。

第50卷第11期 辽 宁 化 工 Vol.50,No.11 2021年11月 Liaoning Chemical Industry November,2021基金项目:广西科技重大专项(项目编号:桂科AA19182014)。
收稿日期: 2021-05-06 作者简介: 李玉婷(1990-),女,广西玉林市人,初级工程师,硕士,2020年毕业于广州大学有机化学专业,研究方向:锂离子电池材料的制备。
利用高密度四氧化三锰制备锰酸锂的研究李玉婷*,莫燕娇,甘永兰,张帆,杨雄强(广西锰华新能源科技发展有限公司,广西 钦州 535000)摘 要:以四氧化三锰和碳酸锂为原料,加入一定量的添加剂,采用高温固相法合成锰酸锂。
利用马弗炉进行n (Li)/n (Mn)比例的不同进行烧结实验,并对锰酸锂样品的中位粒度D 50、比表面积、pH 值、压实密度、放电容量、循环性能、形貌分析等进行测试。
结果表明:实验制备的锰酸锂样品的最佳n (Li)/n (Mn)比为0.595,样品的中位粒度D 50为14.35 μm,pH 值为8.62,压实密度为3.10 g ·cm -3,1C 容量为121.137 mA ·h ·g -1,500次循环容量衰减为12.49%,55 ℃循环500次容量衰减为35.39%,满足动力电池对锰酸锂的要求。
关 键 词:四氧化三锰; 锂锰比; 锰酸锂; 电性能中图分类号:TF111 文献标识码: A 文章编号:1004-0935(2021)11-1615-04锂离子电池凭着自放电率低、便于携带、安全环保等优点成为便携式设备的新一代电池[1]。
常见的锂离子电池正极材料有镍钴锰酸锂三元材料,钴酸锂,磷酸铁锂及锰酸锂。
伴随着锂离子电池的不断发展,尖晶石LiMn 2O 4正极材料因其具有良好的充放电电压平台和较好的热稳定性,且具有资源丰富、成本低、无污染、安全性好等优点,被广泛应用于电池正极材料[2]。

信息论与编码试题集与答案(新)1. 在无失真的信源中,信源输出由 H (X ) 来度量;在有失真的信源中,信源输出由 R (D ) 来度量。
2. 要使通信系统做到传输信息有效、可靠和保密,必须首先信源编码,然后_____加密____编码,再______信道_____编码,最后送入信道。
3. 带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式,也就是有名的香农公式是log(1)C W SNR =+;当归一化信道容量C/W 趋近于零时,也即信道完全丧失了通信能力,此时E b /N 0为-1.6 dB ,我们将它称作香农限,是一切编码方式所能达到的理论极限。
4. 保密系统的密钥量越小,密钥熵H (K )就越小,其密文中含有的关于明文的信息量I (M ;C )就越大。
5. 已知n =7的循环码42()1g x x x x =+++,则信息位长度k 为 3 ,校验多项式 h(x)= 3 1x x ++ 。
6. 设输入符号表为X ={0,1},输出符号表为Y ={0,1}。
输入信号的概率分布为p =(1/2,1/2),失真函数为d (0,0) = d (1,1) = 0,d (0,1) =2,d (1,0) = 1,则D min = 0 ,R (D min )=1bit/symbol ,相应的编码器转移概率矩阵[p(y/x )]=1001??;D max = 0.5 ,R (D max )= 0 ,相应的编码器转移概率矩阵[p(y/x )]=1010??。
7. 已知用户A 的RSA 公开密钥(e,n )=(3,55),5,11p q ==,则()φn = 40 ,他的秘密密钥(d,n )=(27,55) 。
若用户B 向用户A 发送m =2的加密消息,则该加密后的消息为 8 。
二、判断题1. 可以用克劳夫特不等式作为唯一可译码存在的判据。
(√ )2. 线性码一定包含全零码。
(√ )3. 算术编码是一种无失真的分组信源编码,其基本思想是将一定精度数值作为序列的编码,是以另外一种形式实现的最佳统计匹配编码。
第五章习题解答1、给出数据点:013419156i i x y =⎧⎨=⎩(1)用012,,x x x 构造二次Lagrange 插值多项式2()L x ,并计算15.x =的近似值215(.)L 。
(2)用123,,x x x 构造二次Newton 插值多项式2()N x ,并计算15.x =的近似值215(.)N 。
(3)用事后误差估计方法估计215(.)L 、215(.)N 的误差。
解:(1)利用012013,,x x x ===,0121915,,y y y ===作Lagrange 插值函数2202130301191501031013303152933()()()()()()()()()()()()()()i i i x x x x x x L x l x y x x =------==⨯+⨯+⨯-------++=∑代入可得2151175(.).L =。
(2)利用123134,,x x x ===,1239156,,y y y ===构造如下差商表:于是可得插值多项式:229314134196()()()()()N x x x x x x =+-+---=-+-代入可得215135(.).N =。
(3)用事后误差估计的方法可得误差为1501511751350656304.(.)(..).R -=-=-◆ 2、设Lagrange 插值基函数是0012()(,,,,)nj i j i jj ix x l x i n x x =≠-==-∏试证明:①对x ∀,有1()ni i l x ==∑②00110001211()()(,,,)()()nki i i n n k l x k n x x x k n =⎧=⎪==⎨⎪-=+⎩∑其中01,,,n x x x 为互异的插值节点。
证明:①由Lagrange 插值多项式的误差表达式101()()()()()!n ni i f R x x x n ξ+==-+∏知,对于函数1()f x =进行插值,其误差为0,亦即0()()ni ii f x l x f==∑精确成立,亦即1()ni i l x ==∑。
第八章 假 设 检 验三、解答题1. 某种零件的长度服从正态分布,方差σ2 = 1.21,随机抽取6件,记录其长度(毫米)分别为32.46,31.54,30.10,29.76,31.67,31.23在显著性水平α = 0.01下,能否认为这批零件的平均长度为32.50毫米? 解:这是单个正态总体均值比较的问题,若设该种零件的长度),(~2σμN X ,则需要检验的是:00:μμ=H 01:μμ≠H由于2σ已知,选取nX Z σμ0-=为检验统计量,在显著水平α = 0.01下,0H 的拒绝域为:}|{|}|{|005.02Z z Z z ≥=≥α查表得 2.575829005.0=Z ,现由n =6, 31.1266711∑===ni i x n x ,1.1=σ, 50.320=μ计算得:3.0581561.132.5-31.126670==-=nX z σμ005.0Z z >可知,z 落入拒绝域中,故在0.01的显著水平下应拒绝0H ,不能认为这批零件的平均长度为32.50毫米。
EXCEL 实验结果:2. 正常人的脉搏平均每分钟72次,某医生测得10例“四乙基铅中毒”患者的脉搏数如下:54,67,68,78,70,66,67,65,69,70已知人的脉搏次数服从正态分布,问在显著水平α = 0.05下,“四乙基铅中毒”患者的脉搏和正常人的脉搏有无显著差异?解:这是单个正态总体均值比较的问题,若设“四乙基铅中毒”患者的脉搏数),(~2σμN X ,则需要检验的是:00:μμ=H 01:μμ≠H由于方差未知,选取ns X T 0μ-=为检验统计量,在显著水平α = 0.05下,0H 的拒绝域为:)}9(|{|)}1(|{|2/05.02t t n t t ≥=-≥α查表得 2.26215716)9(025.0=t ,现由n =10, 67.411∑===n i i x n x , ()35.155555611122∑==--=n i i x x n s , 计算得2.45335761035.1555556724.670=-=-=nsX t μ)9(025.0t t >可知,t 落入拒绝域中,故在0.05的显著水平下应拒绝0H ,“四乙基铅中毒”患者的脉搏和正常人的脉搏有显著差异。
轮系习题答案一、填空题:1.轮系可以分为:定轴轮系和周转轮系。
2.定轴轮系是指:当轮系运动时,各轮轴线位置固定不动的轮系;周转轮系是指:轮系运动时,凡至少有一个齿轮的轴线是绕另一齿轮的轴线转动的轮系。
3.周转轮系的组成部分包括:太阳轮、行星轮和行星架。
4.行星轮系具有1个自由度,差动轮系有 2自由度。
5、行星轮系的同心条件是指:要使行星轮系能正常运转,其基本构件的回转线必须在同一直线上。
6、确定行星轮系中各轮齿数的条件包括:传动比条件、同心条件、均布条件、邻接条件。
7、正号机构和负号机构分别是指:转化轮系的传动比H 1n i 为正号或者负号的周转轮系。
动力传动中多采用负号机构。
二、分析计算题 1、在图示的车床变速箱中,移动三联齿轮a 使3’和4’啮合。
双移动双联齿轮b 使齿轮5’和6’啮合。
已知各轮的齿数为z 1=42,582=z ,38'3=z ,42'4=z ,48'5=z ,48'6=z 电动机的转速为n 1=1445r/min ,求带轮转速的大小和方向。
解:3858483842484258'5'31'6'426116-==-==z z z z z z n n i min /9466r n -=(与电动机转动方向相反)2、在图示的轮系中,已知各轮齿数为20z z z z z 65321=====,已知齿轮1、4、5、7为同轴线,试求该轮系的传动比17i 。
(1)z z z z z 41231225520100=++==?=z z z z 75612332060=+==?=(2)iz z z z zz z z z z17323467123561=-()=-=-100602020153、在图示轮系中,已知:蜗杆为单头且右旋,转速n11440= r/min,转动方向如图示,其余各轮齿数为:402=z,20'2=z,303=z,18'3=z,544=z,试:(1)说明轮系属于何种类型;(2)计算齿轮4得转速n4;(3)在图中标出齿轮4的转动方向。