结构力学课后答案第6章力法

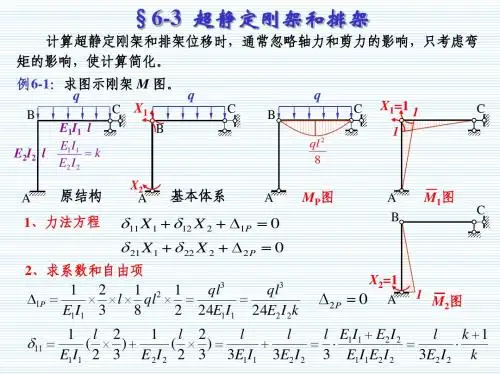
第六章 杆类构件的内力分析6.1。

题6.1图解：（a ）应用截面法：对题的图取截面2-2以下部分为研究对象，受力图如图一所示： 图一图二由平衡条件得：0,AM=∑ 6320N F ⨯-⨯=解得： N F =9KN CD 杆的变形属于拉伸变形。

应用截面法，取题所示截面1-1以右及2-2以下部分作为研究对象，其受力图如图二所示，由平衡条件有：0,O M =∑6210N F M ⨯-⨯-=（1）0,y F =∑60N S F F --=（2）将N F =9KN 代入（1）-（2）式，得： M =3 kN·m S F =3 KN AB 杆属于弯曲变形。

（b ）应用截面法 ，取1-1以上部分作为研究对象，受力图如图三所示，由平衡条件有： 图三NF =2KN0,DM=∑ 210M -⨯= M =2KNAB 杆属于弯曲变形6.2题6.2图解：首先根据刚体系的平衡条件，求出AB 杆的内力。

刚体1的受力图如图一所示图一图二平衡条件为：0,CM=∑104840D NF F ⨯-⨯-⨯=（1） 刚体2受力图如图二所示，平衡条件为：0,EM=∑240N D F F ⨯-⨯= （2）解以上两式有AB 杆内的轴力为：N F =5KN6.3 题6.3图解：（a ） 如图所示，解除约束，代之以约束反力，做受力图，如图1a 所示。

利用静力平衡条件，确定约束反力的大小和方向，并标示在图1a 中，作杆左端面的外法线n ，将受力图中各力标以正负号，轴力图是平行于杆轴线的直线，轴力图线在有轴向力作用处要发生突变，突变量等于该处总用力的数值，对于正的外力，轴力图向上突变，对于负的外力，轴力图向下突变，轴力图如2a 所示，截面1和截面2上的轴力分别为1N F =-2KN 2N F =-8KN ， （b ）解题步骤和（a ）相同，杆的受力图和轴力图如（1b ）（2b ）所示，截面1和截面2上的轴力分别为1N F =4KN 2N F =6KN（c ）解题步骤和（a ）相同，杆的受力图和轴力图如（1c ）（2c ）所示，截面1，截面2和截面3上的轴力分别为1N F =3F2N F =4F ，3N F =4F（d ）解题步骤和（a ）相同，杆的受力图和轴力图如（1d ）（2d ）所示，截面1和截面2上的轴力分别为1N F =2KN 2N F =2KN 6.4。

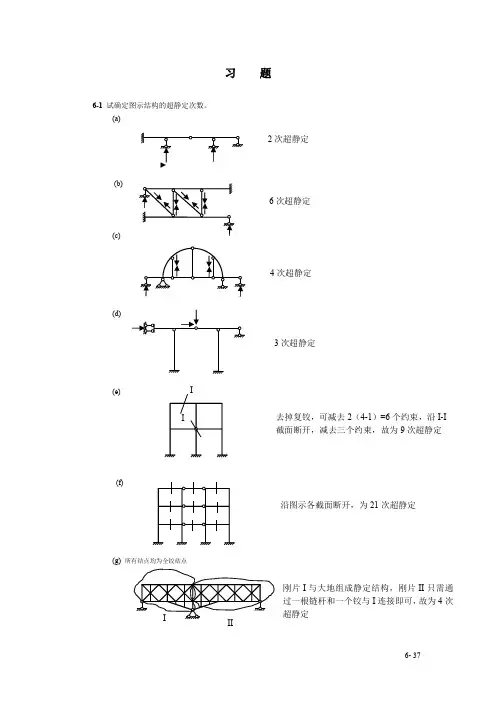
习题6-1试确定图示结构的超静定次数。

(a)(b)(c)(d)(e)(f)(g)所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定II去掉复铰，可减去2（4-1）=6个约束，沿I-I截面断开，减去三个约束，故为9次超静定沿图示各截面断开，为21次超静定I II 刚片I与大地组成静定结构，刚片II只需通过一根链杆和一个铰与I连接即可，故为4次超静定(h)6-2试回答：结构的超静定次数与力法基本结构的选择是否有关？力法方程有何物理意义？6-3试用力法计算图示超静定梁，并绘出M 、F Q 图。

(a)解：上图=l1M pM 01111=∆+p X δ其中：EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EI l F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61F PA2l 3l 3B2EIEIC题目有错误，为可变体系。

+pF p lF 32X 1=1M 图p Q X Q Q +=11p F 21⊕p F 21(b)解：基本结构为：l1M 3l l2M l F p 21pM l F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδp M X M X M M ++=2211pQ X Q X Q Q ++=22116-4试用力法计算图示结构，并绘其内力图。

(a)l2l 2l2lABCD EI =常数F Pl 2E FQ 图F PX 1X 2F P解：基本结构为：1M pM 01111=∆+p X δpM X M M +=11(b)解：基本结构为：EI=常数qACEDB4a 2a4a4a20kN/m3m6m6mAEI 1.75EIB CD 20kN/mX 1166810810计算1M ，由对称性知，可考虑半结构。

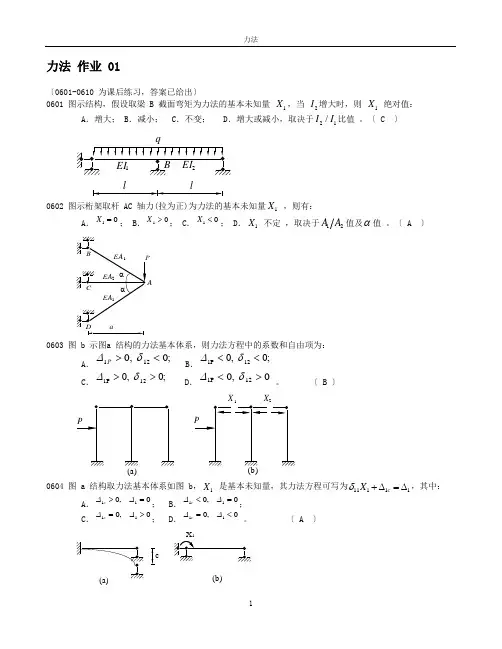
力法 作业 01〔0601-0610 为课后练习，答案已给出〕0601 图示结构，假设取梁 B 截面弯矩为力法的基本未知量 1X ，当 2I 增大时，则 1X 绝对值：A ．增大；B ．减小；C ．不变；D ．增大或减小，取决于21/I I 比值 。

〔 C 〕q0602 图示桁架取杆 AC 轴力(拉为正)为力法的基本未知量1X ，则有：A ．X 10=；B ．X 10>；C ．X 10<；D ．1X 不定 ，取决于12A A 值及α值 。

〔 A 〕aD0603 图 b 示图a 结构的力法基本体系，则力法方程中的系数和自由项为：A ．∆11200P ><,; δB ．∆11200P <<,;δC ．∆11200P >>,;δ D ．∆11200P <>,δ 。

〔 B 〕X X0604 图 a 结构取力法基本体系如图 b ，1X 是基本未知量，其力法方程可写为11111c X δ+∆=∆，其中： A ．∆∆1100c >=,； B ．∆∆1100c<=,；C ．∆∆1100c =>,； D ．∆∆1100c =<, 。

〔 A 〕(a)(b)X 10605 图 a 结构的最后弯矩图为 ：A ．图 b ；B ．图 c ；C ．图 d ；D ．都不 对 。

〔 A 〕l 3M /4M /4(a)(b)M /43M /4M /8M /43M /4M /2(c)(d)0606 图示结构 f (柔 度) 从小到大时，固定端弯矩 m 为：A ．从小到大；B ．从大到小；C ．不变化;D ． m 反向 。

〔 B 〕0607 图示对称结构，其半结构计算简图为图：B.原 图〔 A 〕0608图示结构( f 为柔度)：A ．M MA C >;B ．M M AC =; C ．M M A C <;D ．M M A C =- 。

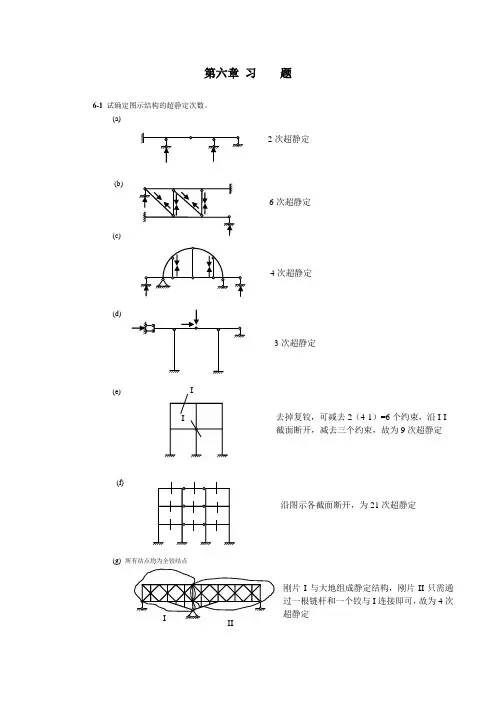
第六章 习 题6-1 试确定图示结构的超静定次数。

(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰，可减去2（4-1）=6个约束，沿I-I 截面断开，减去三个约束，故为9次超静定沿图示各截面断开，为21次超静定刚片I 与大地组成静定结构，刚片II 只需通过一根链杆和一个铰与I 连接即可，故为4次超静定(h)6-2 试回答：结构的超静定次数与力法基本结构的选择是否有关？力法方程有何物理意义？ 6-3 试用力法计算图示超静定梁，并绘出M 、F Q 图。

(a) 解：上图=l1M p M01111=∆+p X δ其中：EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误，为可变体系。

+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解：基本结构为：l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构，并绘其内力图。

(a)l2l 2 l2l l 2Q 图12解：基本结构为：1Mp M01111=∆+p X δ p M X M M +=11(b)解：基本结构为：4a 2a4a4a3m6m 6m810810计算1M，由对称性知，可考虑半结构。

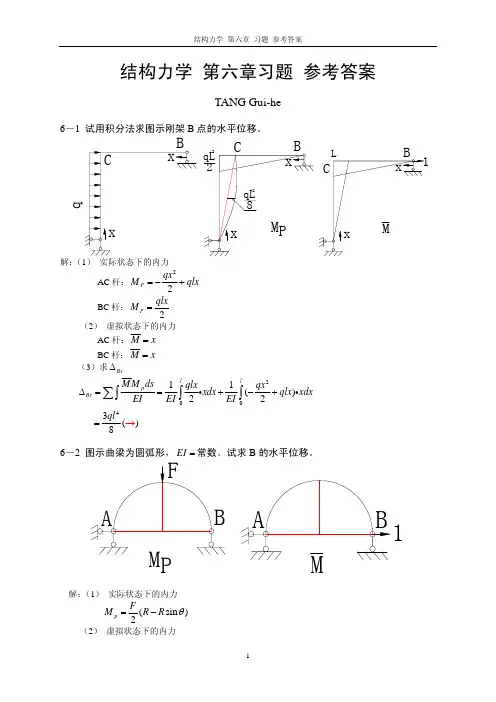
结构力学 第六章习题 参考答案TANG Gui-he6－1 试用积分法求图示刚架B 点的水平位移。

q解：（1） 实际状态下的内力AC 杆：22P qx M qlx =−+BC 杆：2P qlxM =（2） 虚拟状态下的内力AC 杆：M x = BC 杆：M x = （3）求Bx Δ200411()223 ()8l lp Bx M M ds qlx qx xdx qlx xdx EIEI EI qlΔ==+−+=∑∫∫∫i i→6－2 图示曲梁为圆弧形，EI =常数。

试求B 的水平位移。

1解：（1） 实际状态下的内力(sin 2p FM R R )θ=− （2） 虚拟状态下的内力1sin M R θ=i （3）求 Bx Δ/2312(sin )sin 22p Bx M M ds F F R R R Rd EIEIEIπθθθΔ==→−=∑∫∫ii i ()R6－3B AAB解：（1） 实际状态下的内力20sin()(1cos )p M qRd R qR θϕθϕθ=−=−∫i（2） 虚拟状态下的内力1sin M R θ=i（3）求 Bx Δ/2421(1cos )sin ()2p Bx M M ds FR qR R Rd EIEIEIπθθθΔ==←−=∑∫∫i i6－4 图示桁架各杆截面均为，32210m A −=×210 GPa E =，40 kN F =，。

试求：(a) C 点的竖向位移；(b) 角ADC 的改变量。

2 m d =F (kN)NP解： 实际状态下的桁架内力如上图。

（a ）在C 点加上一个单位荷载，得到虚拟状态下的内力如上图。

11[2()(222322]22210)()N Np Cy F F l F d F d EAEA FdEAΔ==−−+↓++=+∑i i i i i i iNPNP（b）虚拟状态下的内力如上图。

11(22()(]4) ()N NpADCF F lF dEA EA dFEAϕ∠Δ==++−=∑ii i i增大6－6 试用图乘法求指定位移。

第6章位移法习题解答习题6.1确定用位移法计算习题6.1图所示结构的基本未知量数目，并绘出基本结构。

（除注明者外，其余杆的EI为常数。

）(a) (b) (c) (d)习题6.1图【解】各题基本未知量（取独立未知结点位移为基本未知量）如下：（a）n=4 （b）n=2 （c）n=6 （d）n=8习题6.2是非判断(1)位移法基本未知量的个数与结构的超静定次数无关。

（）(2)位移法可用于求解静定结构的内力。

（）(3)用位移法计算结构由于支座移动引起的内力时，采用与荷载作用时相同的基本结构。

（）(4)位移法只能用于求解连续梁和刚架，不能用于求解桁架。

（）【解】（1）正确。

位移法求解时基本未知量是结构的未知结点位移，与结构是否超静定无关。

（2）正确。

无任何结点位移发生的静定结构内力图可利用载常数直接确定；有结点位移发生的静定结构则可利用位移法的一般步骤计算。

（3）正确。

用位移法计算支座位移引起的内力时，可采用与荷载作用相同的基本结构，自由项可根据形常数和支移值确定。

（4）错误。

只要能够取得杆端力与杆端位移之间的函数关系，位移法就可用于求解任何杆系结构。

习题6.3已知习题6.3图所示刚架的结点B产生转角θB =π/180，试用位移法概念求解所作用外力偶M。

习题 6.3图【解】30i π 。

发生转角θB 时，可直接求得结点B 所连的各杆端弯矩，再由结点B 的平衡条件即可得M 。

习题6.4 若习题6.4图所示结构结点B 向右产生单位位移，试用位移法中剪力分配法的概念求解应施加的力F P 。

习题 6.4图【解】315lEI。

结点B 向右产生单位位移时，横梁所连各柱端剪力之和即为F P 。

习题6.5 已知刚架的弯矩图如习题6.5图所示，各杆EI =常数，杆长l =4m ，试用位移法概念直接计算结点B 的转角θB 。

m习题 6.5图【解】由M 图可知，BC 杆上无外荷载，其杆端弯矩为330BC BC B M i θ==-，由此求得40B EIθ=-。

第6章力法6.1 复习笔记本章重点介绍了力法的原理以及如何运用力法对超静定结构在各种荷载作用下的内力和位移进行求解。

首先，从单次超静定结构到多次超静定结构，对力法的解题步骤进行了归纳并推导出了力法的典型方程；随后，论述了超静定结构超静定次数的判定方法，演示了刚架、排架、桁架、组合结构、对称结构在荷载作用以及支座移动和温度改变下的力法分析步骤，讨论了基于力法和虚功原理的超静定结构的位移计算思路；最后，强调了超静定结构计算中校核的重要性，以确保最终计算结构的准确性和可靠性。

一、力法的基本概念1．力法的基本未知量、基本体系和基本方程力法的基本概念，包括基本未知量、基本体系、基本结构以及基本方程见表6-1-1，此外，表中还归纳了超静定结构的力法分析步骤。

表6-1-1 力法的基本未知量、基本体系和基本方程2．多次超静定结构的力法分析（见表6-1-2）表6-1-2 多次超静定结构的力法分析步骤3．力法典型方程从一次超静定结构的力法分析到二次超静定结构的力法分析，可以发现一定的规律，那么具有n次超静定结构的力法典型方程归纳如下：式中，ΔiP表示由荷载产生的沿X i方向的位移；δij表示由单位力X j＝1产生的沿X i＝1方向的位移，常称为柔度系数，且δij＝δji。

在解得多余未知力之后，超静定结构的内力可根据叠加原理计算如下：或根据结构受力平衡求解。

二、超静定次数的确定——力法的前期工作（见表6-1-3）表6-1-3 超静定次数的确定——力法的前期工作三、力法解超静定刚架和排架（见表6-1-4）表6-1-4 力法解超静定刚架和排架四、力法解超静定桁架和组合结构（见表6-1-5）表6-1-5 力法解超静定桁架和组合结构五、力法解对称结构（表6-1-6）表6-1-6 力法解对称结构。

结构力学力法习题及答案结构力学力法习题及答案结构力学是一门研究物体在外力作用下产生的应力和变形的学科。

在工程学中，结构力学是非常重要的一门学科，它为我们设计和分析各种建筑和机械结构提供了基础。

在学习结构力学的过程中，习题是必不可少的一部分。

下面将给出一些结构力学的力法习题及其答案，希望对读者有所帮助。

1. 一个悬臂梁上有一个集中力作用在梁的自由端，求该梁的弯矩分布图。

解答：根据悬臂梁的特点，自由端处的弯矩最大。

假设集中力为F，梁的长度为L，弹性模量为E，梁的截面惯性矩为I。

根据悬臂梁的弯矩公式M = F * L，可以得到弯矩分布图为一个从自由端开始逐渐减小的直线。

2. 一个等截面的梁上有一个均布载荷作用，求该梁的剪力分布图。

解答：假设均布载荷为q，梁的长度为L，根据梁的受力平衡条件，可以得到梁上任意一点的剪力大小为V = q * x，其中x为距离梁的一端的距离。

因此，该梁的剪力分布图为一个线性增长的直线。

3. 一个梁上有多个集中力作用，求该梁的弯矩和剪力分布图。

解答：对于每个集中力，可以分别求出其在梁上的弯矩和剪力分布图。

然后将所有的弯矩和剪力分布图叠加在一起，即可得到梁的总弯矩和总剪力分布图。

4. 一个悬臂梁上有一个集中力和一个均布载荷同时作用，求该梁的弯矩和剪力分布图。

解答：首先，根据集中力的大小和悬臂梁的长度，可以求出集中力在悬臂梁上的弯矩分布图。

然后，根据均布载荷的大小和悬臂梁的长度，可以求出均布载荷在悬臂梁上的剪力分布图。

最后，将两者叠加在一起，即可得到梁的总弯矩和总剪力分布图。

5. 一个梁上有多个集中力和多个均布载荷同时作用，求该梁的弯矩和剪力分布图。

解答：对于每个集中力和均布载荷，可以分别求出其在梁上的弯矩和剪力分布图。

然后将所有的弯矩和剪力分布图叠加在一起，即可得到梁的总弯矩和总剪力分布图。

通过以上习题的解答，我们可以看到结构力学中力法的应用。

在实际工程中，我们需要根据具体的结构形式和受力情况，运用结构力学的理论知识，求解结构的受力分布，从而保证结构的安全可靠。