半导体的带间光吸收谱曲线

第五章半导体中的光辐射和光吸收1. 名词解释：带间复合、杂质能级复合、激子复合、等电子陷阱复合、表面复合。

带间复合：在直接带隙的半导体材料中，位于导带底的一个电子向下跃迁，同位于价带顶的一个空穴复合，产生一个光子，其能量大小正好等于半导体材料E。

的禁带宽度g浅杂质能级复合：杂质能级有深有浅，那些位置距离导带底或价带顶很近的浅杂质能级，能与价带之间和导带之间的载流子复合为边缘发射，其光子能量总E小。

比禁带宽度g激子复合：在某些情况下，晶体中的电子和空穴可以稳定地结合在一起，形成一个中性的“准粒子”，作为一个整体存在，即“激子”。

在一定条件下，这些激子中的电子和空穴复合发光，而且效率可以相当高，其复合产生的光子能量小E。

于禁带宽度g等电子陷阱复合：由于等电子杂质的电负性和原子半径与基质原子不同，产生了一个势场，产生由核心力引起的短程作用势，从而形成载流子的束缚态，即陷阱能级，可以俘获电子或空穴，形成等电子陷阱上的束缚激子。

由于它们是局域化的，根据测不准关系，它们在动量空间的波函数相当弥散，电子和空穴的波函数有大量交叠，因而能实现准直接跃迁，从而使辐射复合几率显著提高。

表面复合：晶体表面的晶格中断，产生悬链，能够产生高浓度的深的或浅的能级，它们可以充当复合中心。

通过表面的跃迁连续进行表面复合，不会产生光子，因而是非辐射复合。

2. . 什么叫俄歇复合，俄歇复合速率与哪些因素有关？为什么长波长的InGaAsP 等材料的俄歇复合比短波长材料严重？为什么俄歇复合影响器件的J th 、温度稳定性和可靠性？ 解析：● 俄歇效应是一个有三粒子参与、涉及四个能级的非辐射复合的效应。

在半导体中，电子与空穴复合时，把能量或者动量通过碰撞转移给第三个粒子跃迁到更高能态，并与晶格反复碰撞后失去能量。

这种复合过程叫俄歇复合.整个过程中能量守恒，动量也守恒。

●半导体材料中带间俄歇复合有很多种，我们主要考虑CCHC 过程（两个导带电子与一个重空穴）和CHHS 过程（一个导带电子和两个重空穴）。

半导体材料光学带隙的计算禁带宽度是半导体的一个重要特征参量，其大小主要决定于半导体的能带结构，即与晶体结构和原子的结合性质等有关。

禁带宽度的大小实际上是反映了价电子被束缚强弱程度的一个物理量，也就是产生本征激发所需要的最小能量。

禁带宽度可以通过电导率法和光谱测试法测得,为了区别用电导率法测得禁带宽度值，用光谱测试法测得的禁带宽度值又叫作光学带隙。

下面以光谱测试法为例介绍半导体材料光学带隙的计算方法：对于半导体材料，其光学带隙和吸收系数之间的关系式为[1]：αhν=B(hν-Eg)m （1）其中α为摩尔吸收系数,h为普朗克常数，ν为入射光子频率， B 为比例常数，Eg为半导体材料的光学带隙，m的值与半导体材料以及跃迁类型相关：（1）当m=1/2 时，对应直接带隙半导体允许的偶极跃迁；（2）当m=3/2 时，对应直接带隙半导体禁戒的偶极跃迁；（3）当m=2 时，对应间接带隙半导体允许的跃迁；（4）当m=3 时，对应间接带隙半导体禁戒的跃迁。

下面介绍两种禁带宽度计算公式的推导方法：推导1：根据朗伯比尔定律可知：A=αb c (2)其中 A 为样品吸光度，b 为样品厚度，c 为浓度，其中bc 为一常数，若B1=(B/bc)1/m，则公式(1)可为：(Ahν)1/m=B1(hν-Eg) (3)根据公式(3),若以hν 值为x 轴，以(Ahν)1/m 值为y 轴作图，当y=0 时，反向延伸曲线切线与x 轴相交，即可得半导体材料的光学带隙值Eg。

推导2：根据K-M 公式可知：F(R∞)=(1- R∞)2/2 R∞=K/S (4)其中R∞为绝对反射率(在日常测试中可以用以硫酸钡做参比测得的样品相对反射率代替[2])，K 为吸收系数，S 为散射系数。

若假设半导体材料分散完全或者将样品置于600入射光持续光照下可认为K=2α[3]。

因在一定温度下样品散射系数为一常数，假设比例常数为B2，,我们可通过公式(4)和公式(1)可得：(F(R∞) hν)1/m=B2(hν-Eg) (5)根据公式(5)，若以hν 值为x 轴，以(F(R∞) hν)1/m值为y 轴作图，当y=0 时，反向延伸曲线切线与x 轴相交，即可得半导体材料的光学带隙值Eg。

半导体材料光学带隙的计算禁带宽度是半导体的一个重要特征参量，其大小主要决定于半导体的能带结构，即与晶体结构和原子的结合性质等有关。

禁带宽度的大小实际上是反映了价电子被束缚强弱程度的一个物理量，也就是产生本征激发所需要的最小能量。

禁带宽度可以通过电导率法和光谱测试法测得,为了区别用电导率法测得禁带宽度值，用光谱测试法测得的禁带宽度值又叫作光学带隙。

下面以光谱测试法为例介绍半导体材料光学带隙的计算方法：对于半导体材料，其光学带隙和吸收系数之间的关系式为[1]：αhν=B(hν-Eg)m 〔1〕其中α为摩尔吸收系数,h为普朗克常数，ν为入射光子频率， B 为比例常数，Eg为半导体材料的光学带隙，m的值与半导体材料以及跃迁类型相关：〔1〕当m=1/2 时，对应直接带隙半导体允许的偶极跃迁；〔2〕当m=3/2 时，对应直接带隙半导体禁戒的偶极跃迁；〔3〕当m=2 时，对应间接带隙半导体允许的跃迁；〔4〕当m=3 时，对应间接带隙半导体禁戒的跃迁。

下面介绍两种禁带宽度计算公式的推导方法：推导1：根据朗伯比尔定律可知：A=αb c (2)其中 A 为样品吸光度，b 为样品厚度，c 为浓度，其中bc 为一常数，假设B1=(B/bc)1/m，那么公式(1)可为：(Ahν)1/m=B1(hν-Eg) (3)根据公式(3),假设以hν 值为x 轴，以(Ahν)1/m 值为y 轴作图，当y=0 时，反向延伸曲线切线与x 轴相交，即可得半导体材料的光学带隙值Eg。

推导2：根据K-M 公式可知：F(R∞)=(1- R∞)2/2 R∞=K/S (4)其中R∞为绝对反射率(在日常测试中可以用以硫酸钡做参比测得的样品相对反射率代替[2])，K 为吸收系数，S 为散射系数。

假设假设半导体材料分散完全或者将样品置于600入射光持续光照下可认为K=2α[3]。

因在一定温度下样品散射系数为一常数，假设比例常数为B2，,我们可通过公式(4)和公式(1)可得：(F(R∞) hν)1/m=B2(hν-Eg) (5)根据公式(5)，假设以hν 值为x 轴，以(F(R∞) hν)1/m值为y 轴作图，当y=0 时，反向延伸曲线切线与x 轴相交，即可得半导体材料的光学带隙值Eg。

根据紫外-可见光谱计算半导体能带Eg光学吸收系数满足方程：α=(A/hν)(hν-Eg)1/2，其中A 是比例常数，hν是光子能量，Eg是ZnO的能隙。

Eg可以通过画(αhν)2与hν的曲线，然后把线性部分延长到α=0得出。

这些数据先用excel计算出来，再导入origin画出曲线图，然后做切线，切线与和横坐标的交点数值就是禁带宽度在origin中做曲线的切线的话~那个切点是怎么确定的下一个画切线的插件targent，它会自动画，切点选一个最陡峭的点1.薄膜：需要的数据：薄膜厚度d，透过谱T%，并且还要知道半导体是直接还是间接型。

首先需要求吸收系数（absorption coefficiency, a）a=-ln(T%)/dAα=dhv的计算在origin里进行，大概可以使用hv=1240/(wavelength(nm))得到间接半导体：纵坐标为(ahv)^2，横坐标为hv直接半导体：纵坐标为(ahv)^(1/2)，横坐标为hv最后，做出曲线的切线（这方面我是自己拉一条直线），与横轴的交点就是Eg。

2.粉体：需要的数据：粉体的漫反射谱Rx。

同样也需要换算成吸收系数，使用a=(1-Rx)2/2Rx (这个就是Kubelka-Munk Function)。

其他的就是按照薄膜同样的方法进行了。

当然，这些方法都是近似的，其中还会存在粉体颗粒对光的散射，薄膜岛状结构对光的散射而对最后结果产生的误差，所以，在研究化学和材料方面可以作为一定知道的数据。

方法1：利用紫外可见漫反射测量中的吸光度与波长数据作图，利用截线法做出吸收波长阈值λg(nm)，利用公式 Eg=1240/λg (eV) 计算禁带宽度。

方法2：利用(Ahν)2 对 hν做图，利用直线部分外推至横坐标交点，即为禁带宽度值。

也可利用(Ahν)对 hν做图，利用直线部分外推至横坐标交点，即为禁带宽度值。

前者为间接半导体禁带宽度值，后者为直接半导体禁带宽度值。

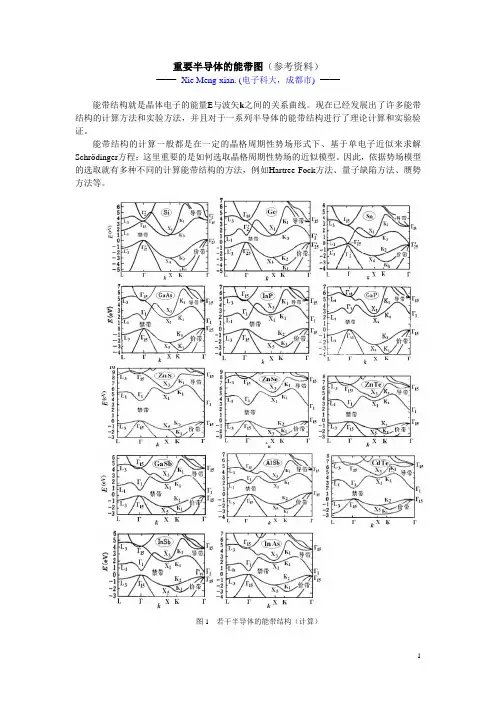
重要半导体的能带图（参考资料）——Xie Meng-xian. (电子科大，成都市)——能带结构就是晶体电子的能量E与波矢k之间的关系曲线。

现在已经发展出了许多能带结构的计算方法和实验方法，并且对于一系列半导体的能带结构进行了理论计算和实验验证。

能带结构的计算一般都是在一定的晶格周期性势场形式下、基于单电子近似来求解Schrödinger方程；这里重要的是如何选取晶格周期性势场的近似模型。

因此，依据势场模型的选取就有多种不同的计算能带结构的方法，例如Hartree-Fock方法、量子缺陷方法、赝勢方法等。

图1 若干半导体的能带结构（计算）图1是采用赝勢方法计算而得到的若干重要半导体的能带结构图（未考虑电子自旋）。

见到，图中所有半导体的价带顶都位于Brillouin区中心（Γ点），然而导带底却不一定；因此就有所谓直接跃迁能带结构的半导体（直接禁带半导体）和间接跃迁能带结构的半导体（间接禁带半导体）之分：Si、Ge、GaP、AlP、AlSb、AlAs等是间接禁带半导体；GaAs、InP、InAs、InSb、GaSb、ZnS、ZnSe、ZnTe、CdTe等是直接禁带半导体。

α-Sn（灰锡）具有金刚石型的晶体结构，它是一种半金属（即禁带宽度为0的半导体）；其他类似的半金属有HgSe和HgTe。

图2～图5示出的是一些重要的宽禁带半导体的能带结构。

这些新型的半导体往往被称为第三代半导体材料（第一代是Si，第二代是GaAs）。

GaN、AlN、InN是直接禁带半导体，SiC、BN是间接禁带半导体。

它们在高功率、高温、微波、低噪声等应用领域内具有优良的性能；特别，氮化镓基的半导体不仅在微波领域、而且在高效率发光（蓝色光）领域内，都表现出了突出的成效。

图2 三种碳化硅的能带结构图3 两种氮化镓的能带结构图4 三种氮化硼的能带结构——————————————————————————图5 氮化铝和氮化铟的能带结构。

半导体材料中的能带理论和光谱学在半导体材料中，能带理论是一个关键的物理学理论。

这个理论解释了为什么半导体材料可以被用于电子学和光电子学。

光谱学也是研究半导体材料的重要领域，它是研究被吸收、发射或散射的光的特性的学科。

在本文中，我们将探讨半导体材料中的能带理论和光谱学。

能带理论半导体材料中的能带理论解释了在材料中的电子是如何被激发和传输的。

在半导体材料中，原子的价电子被束缚在原子核周围，但当多个原子结合在一起，它们的价电子会形成一个更大的能级，称为价带。

电子将填充到最低能级的可用带中，这被称为价带。

价带上方是一个未被填充的能带，被称为能带。

这个未被填充的能带允许电子被激发并移动。

半导体材料的能带结构决定了它们的电学和光学性质。

获得半导体材料中的导电性最关键的是将电子从价带移动到导带中。

受到温度、掺杂和光激发的影响，电子从价带到导带的过程被控制。

半导体材料中的掺杂实际上是通过添加少量的其他元素（称为杂质）来实现的。

通常，掺杂剂会添加强电子或弱电子，通过这些插入的电子来改变材料的导电性质。

这些杂质的掺杂会在价带或导带上产生额外的电荷，从而改变材料的导电性质。

光谱学光谱学是研究半导体材料中光的特性的学科。

光在材料中的行为取决于材料的能带结构和其制造过程。

例如，在半导体材料中加入杂质，可以改变其光学和电学特性。

半导体材料的吸收光谱研究了材料作为吸收体时从光子中吸收的特定能量。

这种吸收与材料的能带结构密切相关。

能带中的电子可以在吸收光子能量后从一个能级跃迁到另一个能级，这种跃迁被称为激发。

根据能带结构的不同，在不同材料中观察到的这些吸收谱也会有所不同。

射频场的辐射也是研究半导体材料的重要光学手段之一。

通过向材料施加高频电场，可以产生强大的射频辐射，进而形成一些新的光谱现象。

例如，在一些较新的研究中，人们使用磁共振技术研究了半导体样品的输运过程。

在光电子学中，光谱学也非常重要。

例如，在半导体激光器中，反向操作电子跃迁导致光放大，这进一步增强了光与半导体材料之间的相互作用。

半导体带隙与波长的关系
半导体材料的电子结构中存在能带，其中被占据的价带和未被占据的导带之间的能量差被称为带隙。

半导体的光电性质与其带隙密切相关，因为只有光子能量高于带隙能量时，才能激发出载流子。

因此，半导体的带隙大小决定了其最大吸收波长和最大发射波长。

根据波长和能量的关系 E=hv，其中E表示光子能量，h为普朗克常数，v为光的频率。

因此，通过转换可得：E=hc/λ，其中λ为光的波长，c为光速。

因此，可以得到半导体的带隙能量 Eg 与其最大吸收波长λmax 和最大发射波长λmin 之间的关系为：
Eg = hc/λmax = hc/λmin
因此，可以看出，半导体的带隙能量与其最大吸收波长和最大发射波长呈反比关系。

当带隙能量较大时，半导体的最大吸收波长也会相应缩短，而最大发射波长会相应增加。

反之，当带隙能量较小时，半导体的最大吸收波长会相应增加，而最大发射波长则会相应缩短。

在半导体器件的应用中，需要根据具体需求选择合适的材料，以实现所需的光电性质和波长范围。

例如，用于光通信的激光器需要具有适当的发射波长，因此需要选择具有合适带隙能量的半导体材料进行制备。

- 1 -。

半导体的带间光吸收谱曲线Xie Meng-xian. (电子科大，成都市)（1）光吸收系数：半导体吸收光的机理主要有带间跃迁吸收（本征吸收）、载流子吸收、晶格振动吸收等。

吸收光的强弱常常采用描述光在半导体中衰减快慢的参量——吸收系数α来表示；若入射光强为I，光进入半导体中的距离为x，则定义：吸收系数的单位是cm-1。

（2）带间光吸收谱曲线的特点：对于Si和GaAs的带间跃迁的光吸收，测得其吸收系数a与光子能量hν的关系如图1所示。

这种带间光吸收谱曲线的特点是：①吸收系数随光子能量而上升；②各种半导体都存在一个吸收光子能量的下限（或者光吸收长波限——截止波长），并且该能量下限随着温度的升高而减小（即截止波长增长）；③GaAs的光吸收谱曲线比Si的陡峭。

为什么半导体的带间光吸收谱曲线具有以上一些特点呢？——与半导体的能带结构有关。

（3）对带间光吸收谱曲线的简单说明：①因为半导体的带间光吸收是由于价带电子跃迁到导带所引起的，则光吸收系数与价带和导带的能态密度有关。

而在价带和导带中的能态密度分布较复杂（在自由电子、球形等能面近似下，能态密度与能量是亚抛物线关系），不过在价带顶和导带底附近的能态密度一般都很小，因此，发生在价带顶和导带底附近之间跃迁的吸收系数也就都很小；随着能量的升高，能态密度增大，故吸收系数就相应地增大，从而使得吸收谱曲线随光子能量而上升。

但是由于实际半导体能带中能态密度分布函数的复杂性，而且电子吸收光的跃迁还必须符合能量守恒、动量守恒和量子力学的跃迁规则——选择定则，所以就导致半导体光吸收谱曲线变得很复杂，可能会出现如图1所示的台阶和多个峰值或谷值。

②因为价电子要能够从价带跃迁到导带，至少应该吸收禁带宽度Eg大小的能量，这样才能符合能量守恒规律，所以就存在一个最小的光吸收能量——光子能量的下限，该能量下限也就对应于光吸收的长波限——截止波长λg ：一些用于光电探测器的半导体的禁带宽度、截止波长和带隙类型，如下表所示。

吸收光谱计算带隙
吸收光谱是用于计算半导体材料带隙的一种常用方法。

其基本原理是通过光谱吸收峰位置和强度的变化来确定半导体材料的带隙大小。

计算步骤如下：
1. 通过紫外-可见光谱仪测量样品的光吸收谱。

这种谱在可见光和紫外光区域内，大部分是由电子跃迁引起的。

2. 找到吸收谱中最强的峰，也就是所谓的“吸收边缘”，其波长为λ1。

3. 根据半导体材料能带结构的理论，带隙Eg等于光子能量hν（h是普朗克常数，ν是光子频率）与光子波长λ之间的关系，即：
Eg = hc/λ- α（hν- E0）
其中，c是光速，α是一个常数，E0是半导体的本征能量。

4. 将吸收边缘的波长λ1带入上述公式计算出带隙值Eg。

需要注意的是，实际计算中还需考虑到半导体材料的表面态、激子效应和温度等因素的影响，从而得到更加准确的带隙值。

石家庄铁道大学实验报告课程名称分院班组桌号实验者姓名实验日期年月日评分教师签名一、实验目的1. 学习紫外分光光度计的工作原理和使用方法。

2. 学习用紫外分光光度计测量样品的透射光谱。

3. 能根据吸收光谱推算出材料的光学禁带。

二、实验内容1. 用紫外分光光度计测量TiO 2溶液的透射光谱；2. 用不同的你和关系计算出TiO 2的光学禁带宽度，并与理论值比较，定它们的跃迁类型。

三、实验原理1. 任何一种物质对光波都会或多或少地吸收，电子由带与带之间的跃迁所形成的吸收过程称为本征吸收。

在本征吸收中，光照将价带中的电子激发到导带，形成电子-空穴对。

本征吸收光子的能量满足：0g hv hv E ≤=0c v λ=01240gnm E λ= 电子在跃迁过程中，导带极小值和价带极大值对应于相同的波矢，成为直接跃迁。

在直接跃迁中，如果对于任何K 的跃迁都是允许的，则吸收系数与带隙的关系为12()g hv A hv E α=-电子在跃迁过程中，导带极小值和价带极大值对应于不同的波矢，称为间接跃迁。

在间接跃迁中，K 空间电子吸收光子从价带顶K 跃迁到导带底部状态K ’，伴随着吸收或者发出声子。

则吸收系数与带隙的关系为2()g hv A hv E α=-2. 透射率、吸光度与吸收系数之间的关系吸光度A 与透射率T 的关系为110T A =㏒吸光规律0=exp -x I I α（） α为吸收系数，x 为光的传播距离，根据朗伯-比尔定律，A 正比于α。

四、实验方法1. 用分析天平去一定量的TiO 2固体样品，溶于的一定量去离子水中，并计算TiO 2的物质的量浓度。

2. 打开722型紫外-可见分光光度计，预热10min 。

3. 讲分别装有去离子水和TiO 2水溶液的石英比色皿放置于参比池和样品池，将仪器的波长调为λ=320nm 。

先用去离子水作为参比溶液，调节仪器透光率T=0和T=100%，然后测试样品池中TiO 2水溶液的吸光度。

半导体材料能带测试及计算对于半导体，是指常温下导电性能介于导体与绝缘体之间的材料，其具有一定的带隙(E g)。

通常对半导体材料而言，采用合适的光激发能够激发价带(VB)的电子激发到导带(CB)，产生电子与空穴对。

图1. 半导体的带隙结构示意图。

在研究中，结构决定性能，对半导体的能带结构测试十分关键。

通过对半导体的结构进行表征，可以通过其电子能带结构对其光电性能进行解析。

对于半导体的能带结构进行测试及分析，通常应用的方法有以下几种(如图2)：1.紫外可见漫反射测试及计算带隙E g；2.VB XPS测得价带位置(E v)；3.SRPES测得E f、E v以及缺陷态位置；4.通过测试Mott-Schottky曲线得到平带电势；5.通过电负性计算得到能带位置.图2. 半导体的带隙结构常见测试方式。

1.紫外可见漫反射测试及计算带隙紫外可见漫反射测试2.制样：背景测试制样：往图3左图所示的样品槽中加入适量的BaSO4粉末（由于BaSO4粉末几乎对光没有吸收，可做背景测试），然后用盖玻片将BaSO4粉末压实，使得BaSO4粉末填充整个样品槽，并压成一个平面，不能有凸出和凹陷，否者会影响测试结果。

样品测试制样：若样品较多足以填充样品槽，可以直接将样品填充样品槽并用盖玻片压平；若样品测试不够填充样品槽，可与BaSO4粉末混合，制成一系列等质量分数的样品，填充样品槽并用盖玻片压平。

图3. 紫外可见漫反射测试中的制样过程图。

1.测试：用积分球进行测试紫外可见漫反射（UV-Vis DRS），采用背景测试样（BaSO4粉末）测试背景基线（选择R%模式），以其为background测试基线，然后将样品放入到样品卡槽中进行测试，得到紫外可见漫反射光谱。

测试完一个样品后，重新制样，继续进行测试。

•测试数据处理数据的处理主要有两种方法：截线法和Tauc plot法。

截线法的基本原理是认为半导体的带边波长（λg）决定于禁带宽度E g。