北师大版初一数学下册对顶角、余角、补角
- 格式:doc
- 大小:399.50 KB
- 文档页数:7

北师大版七年级数学下册精品教案《2.1 第1课时对顶角、余角和补角》.pdf一. 教材分析本节课的主题是对顶角、余角和补角。
这是初中数学的基础知识,对于学生掌握数学的基本概念和几何知识具有重要意义。
通过本节课的学习,学生可以了解到对顶角、余角和补角的定义和性质,并能够运用这些知识解决实际问题。
二. 学情分析学生在进入本节课的学习之前,已经掌握了角的初步知识,对于角的分类和度量有一定的了解。
但是,对于对顶角、余角和补角的概念和性质可能还不够清晰,需要通过本节课的学习来进一步深化理解。
三. 教学目标1.了解对顶角、余角和补角的定义和性质。
2.能够运用对顶角、余角和补角的知识解决实际问题。
3.培养学生的空间想象能力和逻辑思维能力。
四. 教学重难点1.对顶角、余角和补角的定义和性质。
2.运用对顶角、余角和补角的知识解决实际问题。
五. 教学方法采用讲授法、案例分析法、小组合作法等多种教学方法,引导学生通过观察、思考、讨论等方式,自主探索对顶角、余角和补角的知识。
六. 教学准备1.教学PPT。
2.几何图形模板。
3.练习题。
七. 教学过程1.导入(5分钟)通过一个简单的几何图形,引导学生观察其中的对顶角、余角和补角,激发学生的学习兴趣,引出本节课的主题。
2.呈现(10分钟)讲解对顶角、余角和补角的定义和性质,通过PPT展示相关的几何图形,让学生直观地理解这些概念。
3.操练(10分钟)让学生分组合作,利用几何图形模板,自己动手操作,验证对顶角、余角和补角的性质。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)出示一些练习题,让学生独立完成,巩固对顶角、余角和补角的知识。
教师选取部分题目进行讲解,分析解题思路。
5.拓展(10分钟)出示一些实际问题,让学生运用对顶角、余角和补角的知识解决。
教师引导学生进行分析,指导解题方法。
6.小结(5分钟)对本节课的内容进行简要回顾,强调对顶角、余角和补角的定义和性质,提醒学生注意在实际问题中的运用。




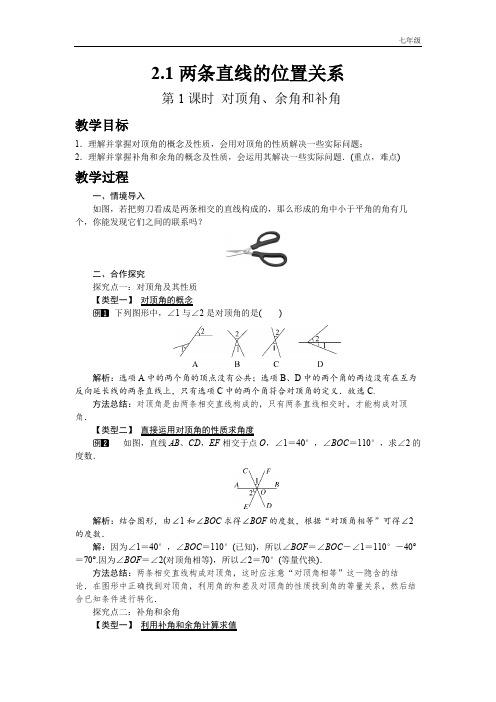
2.1两条直线的位置关系第1课时对顶角、余角和补角教学目标1.理解并掌握对顶角的概念及性质,会用对顶角的性质解决一些实际问题;2.理解并掌握补角和余角的概念及性质,会运用其解决一些实际问题.(重点,难点) 教学过程一、情境导入如图,若把剪刀看成是两条相交的直线构成的,那么形成的角中小于平角的角有几个,你能发现它们之间的联系吗?二、合作探究探究点一:对顶角及其性质【类型一】对顶角的概念下列图形中,∠1与∠2是对顶角的是( )解析:选项A中的两个角的顶点没有公共;选项B、D中的两个角的两边没有在互为反向延长线的两条直线上,只有选项C中的两个角符合对顶角的定义.故选C.方法总结:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.【类型二】直接运用对顶角的性质求角度如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.解析:结合图形,由∠1和∠BOC求得∠BOF的度数,根据“对顶角相等”可得∠2的度数.解:因为∠1=40°,∠BOC=110°(已知),所以∠BOF=∠BOC-∠1=110°-40°=70°.因为∠BOF=∠2(对顶角相等),所以∠2=70°(等量代换).方法总结:两条相交直线构成对顶角,这时应注意“对顶角相等”这一隐含的结论.在图形中正确找到对顶角,利用角的和差及对顶角的性质找到角的等量关系,然后结合已知条件进行转化.探究点二:补角和余角【类型一】利用补角和余角计算求值已知∠A 与∠B 互余,且∠A 的度数比∠B 度数的3倍还多30°,求∠B 的度数.解析:根据∠A 与∠B 互余,得出∠A +∠B =90°,再由∠A 的度数比∠B 度数的3倍还多30°,从而得到∠A =3∠B +30°,再把两个算式联立即可求出∠2的值.解:∵∠A 与∠B 互余,∴∠A +∠B =90°.又∵∠A 的度数比∠B 度数的3倍还多30°,∴设∠B =x ,∴∠A =3∠B +30°=3x +30°,∴3x +30°+x =90°,解得x =15°,故∠B 的度数为15°.方法总结:此题把角的关系结合方程问题一起解决,即把相等关系的问题转化为方程问题,利用方程来解决.【类型二】 补角、余角和角平分线的综合计算如图,已知∠AOB 在∠AOC 内部,∠BOC =90°,OM 、ON 分别是∠AOB ,∠AOC 的平分线,∠AOB 与∠COM 互补,求∠BON 的度数.解析:根据补角的性质,可得∠AOB +∠COM =180°.根据角的和差,可得∠AOB +∠BOM =90°.根据角平分线的性质,可得∠BOM =∠AOB .根据解方程,可得∠AOB 的度12数.根据角的和差,可得答案.解:∵∠AOB 与∠COM 互补,∴∠AOB +∠COM =180°,即∠AOB +∠BOM +∠COB =180°.∵∠COB =90°,∴∠AOB +∠BOM =90°.∵OM 是∠AOB 的平分线,∴∠BOM =∠AOB ,即∠AOB +∠AOB =90°,解得∠AOB =60°,∴∠AOC =∠BOC +∠1212AOB =90°+60°=150°.∵ON 平分∠AOC 得∠AON =∠AOC =×150°=75°.由角的和1212差,∴∠BON =∠AON -∠AOB =75°-60°=15°.方法总结:本题考查了余角与补角及角平分线的相关知识,利用了补角的性质,角的和差,角平分线的性质进行计算,解决问题一定要结合图形认真分析,做到数形结合.【类型三】 补角和余角的性质如图,将一副直角三角尺的直角顶点C 叠放在一起.(1)如图①,若CE 是∠ACD 的角平分线,那么CD 是∠ECB 的角平分线吗?并简述理由;(2)如图②,若∠ECD =α,CD 在∠BCE 的内部,请你猜想∠ACE 与∠DCB 是否相等?并简述理由;(3)在(2)的条件下,请问∠ECD 与∠ACB 的和是多少?并简述理由.解析:(1)首先根据直角三角板的特点得到∠ACD =90°,∠ECB =90°.再根据角平分线的定义计算出∠ECD 和∠DCB 的度数即可;(2)∠ACE 与∠DCB 相等,根据“等角的余角相等”即可得到答案;(3)根据角的和差关系进行等量代换即可.解:(1)CD是∠ECB的角平分线.理由如下:∵∠ACD=90°,CE是∠ACD的角平分线,∴∠ECD=45°.∵∠ECB=90°,∴∠DCB=90°-45°=45°,∴∠ECD=∠DCB,∴CD是∠ECB的角平分线;(2)∠ACE=∠DCB.理由如下:∵∠ACD=90°,∠BCE=90°,∠ECD=α,∴∠ACE=90°-α,∠DCB=90°-α,∴∠ACE=∠DCB;(3)∠ECD+∠ACB=180°.理由如下:∠ECD+∠ACB=∠ECD+∠ACE+∠ECB=∠ACD+∠ECB=90°+90°=180°.方法总结:此题主要查考了角的计算,关键是根据图形分清角之间的和差关系.三、板书设计1.对顶角相等;2.同角或等角的补角相等,同角或等角的余角相等.教学反思本节课学习了对顶角及其性质.教学中可让学生自己画这些角,结合图形说出对顶角的特征.对顶角的识别是易错点,可以结合例题进行练习,让学生在学习中不断纠错,不断进步。
2. 1两条直线的地点关系第 1 课时对顶角、补角和余角1.理解并掌握对顶角的观点及性质,会用对顶角的性质解决一些实质问题;2.理解并掌握补角和余角的观点及性质,会运用其解决一些实质问题.(要点,难点 )一、情境导入如图,若把剪刀当作是两条订交的直线组成的,那么形成的角中小于平角的角有几个,你能发现它们之间的联系吗?二、合作研究研究点一:对顶角及其性质【种类一】对顶角的观点以下图形中,∠ 1 与∠ 2 是对顶角的是()分析:选项 A 中的两个角的极点没有公共;选项 B、 D 中的两个角的两边没有在互为反向延伸线的两条直线上,只有选项 C 中的两个角切合对顶角的定义.应选 C.方法总结:对顶角是由两条订交直线组成的,只有两条直线订交时,才能组成对顶角.【种类二】直接运用对顶角的性质求角度如图,直线AB、 CD, EF 订交于点O,∠ 1= 40°,∠ BOC=110°,求∠ 2 的度数.分析:联合图形,由∠ 1 和∠ BOC 求得∠ BOF 的度数,依据“对顶角相等”可得∠2 的度数.解:由于∠ 1= 40°,∠ BOC= 110° ( 已知 ),因此∠ BOF=∠ BOC-∠ 1= 110°- 40°= 70°.由于∠ BOF =∠ 2(对顶角相等 ),因此∠ 2=70° (等量代换 ).方法总结:两条订交直线组成对顶角,这时应注意“ 对顶角相等”这一隐含的结论.在图形中正确找到对顶角,利用角的和差及对顶角的性质找到角的等量关系,而后联合已知条件进行转变.研究点二:补角和余角【种类一】利用补角和余角计算求值已知∠ A 与∠ B 互余,且∠ A 的度数比∠ B 度数的 3 倍还多 30°,求∠ B 的度数.分析:依据∠ A 与∠ B 互余,得出∠ A+∠ B= 90°,再由∠A 的度数比∠ B 度数的 3 倍还多 30°,进而获得∠ A= 3∠ B+30°,再把两个算式联立刻可求出∠2的值.解:∵∠ A 与∠ B 互余,∴∠ A+∠ B= 90° .又∵∠ A 的度数比∠ B 度数的 3 倍还多 30°,∴设∠ B= x,∴∠ A=3∠ B+30°= 3x+ 30°,∴ 3x+ 30°+ x= 90°,解得 x= 15°,故∠ B 的度数为15° .方法总结:本题把角的关系联合方程问题一同解决,题,利用方程来解决.【种类二】补角、余角和角均分线的综共计算即把相等关系的问题转变为方程问如图,已知∠ AOB 在∠ AOC 内部,∠ BOC= 90°, OM、 ON 分别是∠ AOB,∠AOC 的均分线,∠ AOB 与∠ COM 互补,求∠ BON 的度数.分析:依据补角的性质,可得∠AOB+∠ COM = 180° .依据角的和差,可得∠AOB +∠ BOM = 90° .依据角均分线的性质,可得∠ BOM = 1∠ AOB.依据解方程,可得2∠ AOB的度数.依据角的和差,可得答案.解:∵∠ AOB 与∠ COM 互补,∴∠ AOB+∠ COM = 180°,即∠ AOB+∠ BOM +∠ COB =180° .∵∠ COB=90°,∴∠ AOB+∠ BOM = 90° .∵OM 是∠ AOB 的均分线,∴∠ BOM=1∠ AOB,即∠ AOB+1∠ AOB=90°,解得∠ AOB= 60°,∴∠ AOC=∠ BOC+∠ AOB=2290°+ 60°=150 °.∵ ON 均分∠ AOC 得∠ AON =1∠ AOC =1× 150°= 75°.由角的和差,∴∠22BON =∠ AON-∠ AOB= 75°- 60°= 15°.方法总结:本题考察了余角与补角及角均分线的有关知识,利用了补角的性质,角的和差,角均分线的性质进行计算,解决问题必定要联合图形仔细剖析,做到数形联合.【种类三】补角和余角的性质如图,将一副直角三角尺的直角极点 C 叠放在一同.(1)如图①,若 CE 是∠ ACD 的角均分线,那么CD 是∠ ECB 的角均分线吗?并简述理由;(2)如图②,若∠ ECD =α,CD 在∠ BCE 的内部,请你猜想∠ACE 与∠ DCB 能否相等?并简述原因;(3)在 (2)的条件下,请问∠ECD 与∠ ACB 的和是多少?并简述原因.分析: (1)第一依据直角三角板的特色获得∠ ACD=90°,∠ ECB=90° .再依据角均分线的定义计算出∠ ECD 和∠DCB 的度数即可; (2)∠ ACE 与∠ DCB 相等,依据“等角的余角相等”即可获得答案; (3)依据角的和差关系进行等量代换即可.解: (1)CD 是∠ ECB 的角均分线.原因以下:∵∠ ACD =90°, CE 是∠ ACD 的角均分线,∴∠ ECD = 45° .∵∠ ECB= 90°,∴∠ DCB = 90°- 45°= 45°,∴∠ ECD =∠ DCB,∴CD 是∠ ECB 的角均分线;(2)∠ ACE=∠ DCB .原因以下:∵∠ ACD= 90°,∠ BCE= 90°,∠ ECD =α,∴∠ACE = 90°-α,∠ DCB = 90°-α,∴∠ ACE=∠ DCB ;(3)∠ ECD +∠ ACB = 180 °.原因以下:∠ECD +∠ ACB =∠ ECD +∠ ACE +∠ ECB =∠ACD +∠ ECB= 90°+ 90°= 180° .方法总结:本题主要查考了角的计算,要点是依据图形分清角之间的和差关系.三、板书设计1.对顶角相等;2.同角或等角的补角相等,同角或等角的余角相等.本节课学习了对顶角及其性质.教课中可让学生自己画这些角,联合图形说出对顶角的特色.对顶角的辨别是易错点,能够联合例题进行练习,让学生在学习中不停纠错,不停进步。
数学教学设计
6.3余角、补角、对顶角(2)
【教学目标】:
1、知道对顶角的定义,会画一个已知角的对顶角。
2、知道对顶角相等,并能用它解决一些简单的实际问题。
3、经历观察、操作、说理、交流等过程,进一步发展推理能力。
4、让学生经历从复杂图形中分解出基本图形的过程,渗透化归思想。
【教学重点、难点及解决办法】
教学重点:对顶角的概念及其性质
教学难点:利用对顶角相等解决一些简单的问题
解决办法:强调图形的基本特征,逐步培养学生的审题、识图和推理能力。
【学情分析】
学生已经初步认识了两条直线相交的情况,能够找出其中的邻补角,知道一对邻补角的位置特征和数量关系,并能解决一些简单的几何问题。
在学习方法和能力上,学生已经具备了初步的自学、讨论、观察、操作、说理等方法和能力,这都为本节课教学活动的开展提供了有力的知识和能力背景。
【教学准备】
课件,直尺或三角尺
【教学过程】
一、创设情境,生成新知
师:生活中,要测量两堵墙所成的角的度数,但人不能进入围墙,该如何测量?(课件出示下图)
生1:通过测量AOB
∠的邻补角的大小,计算出AOB
∠的度数。
师:具体地如何操作呢?
生1:延长AO ,在AO 的延长线上取一点记作C ,测量BOC ∠的度数,则
BOC AOB ∠-=∠︒180。
师:(课件展示)很好。
我们通过测量可以测出角的度数,进一步可以算出未知角的度数。
那么,还有其他方法吗?
生2:还可以延长BO ,测量AOD ∠的度数,AOD AOB ∠-=∠︒180。
师:(课件展示)正确。
同样是利用邻补角的知识。
师:如图,我们发现AOB ∠的邻补角有两个,分别是BOC ∠和AOD ∠,那么,这两个角的顶点和两条边分别有什么关系呢?
生3:BOC ∠和AOD ∠的顶点都是O ,边OB 与边OD 共线,边OC 与边OA 共
线。
生4:它们有公共顶点O ,BOC ∠的边OC 是AOD ∠的边OA 的反向延长线,边OB 是AOD ∠的边OD 的反向延长线。
师:同学们回答的都很好。
简单的说,BOC ∠和AOD ∠有公共顶点,且角的两边互为反向延长线。
师:如图,像这样,有公共顶点,且角的两边互为反向延长线的两个角叫做对顶角。
(课件展示,板书对顶角的定义)
因此,1∠与3∠是对顶角。
师:图中还有对顶角吗? 生5:2∠与4∠
师:好,请坐。
【评析】 生活情境导入,不仅激发了学生学习的兴趣,更重要的是诱发了学生探索,获取知识的欲望,生成新知,并形象地认识了对顶角的位置特征。
同时在潜意识里让学生意识到拥有数学知识的重要性,体会数学来源于生活,并应用于生活。
紧扣对顶角的定义,强调以下两点: (1) 对顶角成对出现。
(2) 对顶角需满足有公共顶点,且角的两边互为反向延长线。
巩固练习:
1、 判断:相等的角是对顶角
2、 说一说:下列各图中,1∠和2∠是对顶角吗?为什么?
【评析】 本组题目主要是为了巩固对顶角的概念,通过练习,使学生掌握辨别对顶角的两点要求,同时利用反例验证概念,使学生加深印象,而且最后一幅图也为探讨对顶角的性质做铺垫。
二、积极诱导,再生新知
师:如图,具有特殊位置关系的对顶角有何数量关系呢?为什么? 例如: BOC ∠和AOD ∠(即1∠和2∠) (课件展示)
B
C
D
A
O
1
2
同学们以小组为单位讨论。
生1:相等。
因为这两个角都是BOD ∠的邻补角。
师:非常好。
同学们都知道同角的补角相等,因此BOD ∠的补角BOC ∠和
AOD ∠相等。
师:那么,同学们会不会用完整的说理过程说明呢? 生:能。
生1: Θ BOC ∠+BOD ∠=180︒ AOD ∠+BOD ∠=180︒
∴BOC ∠=AOD ∠(同角的补角相等) 师:同样的,我们也可以利用AOC ∠进行说明。
过程为: 生: Θ BOC ∠+AOC ∠=180︒ AOD ∠+AOC ∠=180︒
∴BOC ∠=AOD ∠(同角的补角相等)
师:因此,我们得出了对顶角的重要性质:对顶角相等。
(板书) 强调指出:“对顶角相等”这一性质是由于对顶角特殊的位置关系而推到的数量关系,数形结合。
若在今后碰到对顶角这样的已知条件,可以利用对顶角相等。
【评析】 在启发学生认识对顶角,并归纳出概念的基础上,学生不难得出对顶角相等的性质。
让学生分组讨论,充分发挥学生学习的主动性,不仅活跃了课堂气氛,更重要的是培养了学生的推理和逻辑思维能力。
三、例题讲解
例1:如图,直线AB 、CD 相交于点O ,OE 平分AOC ∠,︒=∠25AOE ,求BOD ∠的度数?
B
C
D
A
O
E
分析:要求BOD ∠的度数,根据对顶角相等,只需求出其对顶角AOC ∠的度数。
又因为OE 平分AOC ∠,所以AOE AOC ∠=∠2。
而︒=∠25AOE ,所以问题得到了解决。
解: Θ OE 平分AOC ∠
∴ AOE AOC ∠=∠2(角平分线的定义) 又Θ ︒=∠25AOE ∴ ︒=∠50AOC
∴ ︒=∠=∠50AOC BOD (对顶角相等)
变一变:如图,直线AC 、DE 相交于点O ,OE 是∠AOB 的平分线,∠COD=50°,试求∠AOB 的度数。
C
A
D
O
E
B
【评析】 通过本例题的讲解,一方面巩固了对顶角的性质,另一方面让学生体会了几何说理题中由已知条件归纳结论,由问题进行逆向推理的有机结合,为今后的几何学习打下基础。
另外,在讲解过程中注重学生的配合,让学生们参与进来,尝试着分析题目,理解推理过程,从而有条理的写出说理过程。
四、巩固练习
1、如图,直线AB 、EF 相交于点D ,∠ADC=90°。
A
B
C
D
E
F
1
2
(1)1∠的对顶角是______;2∠的余角有___________。
(2)若1∠与2∠的度数之比为1︰4,求BDF ∠的度数。
说明:在找某个角的余角或补角时,不要忘记了一些相等的角(例如对顶角)。
2、如图,AB 、CD 相交于点O ,∠DOE=90°,∠AOC=72°。
求∠BOE 的度数。
A B
D
C
E
O
【评析】 练习题让学生独立思考,大胆尝试。
首先要求做到分析问题的思路清
晰,虽然还有部分学生的说理过程不是很流畅,但通过学生板演,集体讲评纠正
后,学生们对分析问题,并相应的写出清晰的过程印象更加深刻。
这样,逐步培养学生的审题、识图推理能力,更有利于学生今后灵活运用知识,举一反三。
五、延伸与拓展
找找规律——数对顶角
方法一:两条直线相交于一点,得到两对对顶角;三条直线相交于一点,只需在两条直线相交的基础上,看第三条直线与哪些直线相交,相交一次得两对对顶角;四条直线相交于一点,在三条直线相交的基础上,看第四条直线与哪些直线相交,同样的,相交一次得两对对顶角;如此类推,便可以从中总结出规律,计算出n条直线相交于一点,有多少对对顶角。
方法二:首先选定一条边,按顺时针或逆时针的顺序依次标角——标单个的角,两个一组合的角,三个一组合的角等等;然后依次选下一条边,重复刚才的标角操作,边标记边数角,直到标记的角开始重复结束。
如此类推,便可以从中总结出规律,计算出n条直线相交于一点,有多少对对顶角。
【评析】教学时立足于巩固“对顶角的概念”这一基本要求,又敢于提高难度,延伸与拓展,追求一种更高的境界,关注学生细致观察、有条理的思考的能力训练。
不仅让学生学习、掌握知识,更要让学生具备数学的眼睛、数学的头脑,从复杂几何图形中分解出基本图形,探索数学规律。
六、实际应用
学习了对顶角的概念及其性质后,您对于测量两堵墙所成的角的度数问题,还有其他方法吗?
【评析】由测量两堵墙所成的角的度数问题,利用邻补角引出对顶角,最后,再次利用对顶角相等解决此实际问题,首尾呼应,使学生加深了对知识的理解。
七、课堂小结
1、对顶角的定义
2、对顶角的性质
3、会画一个对顶角
【评析】课堂小结以提问形式,由学生自己讨论,归纳总结,不仅培养了学生的概括表达能力,而且让学生对本节课内容有了整体把握,环环相扣,形散而神不散。
八、布置作业:课本P162 习题6.3。