下载文档原格式
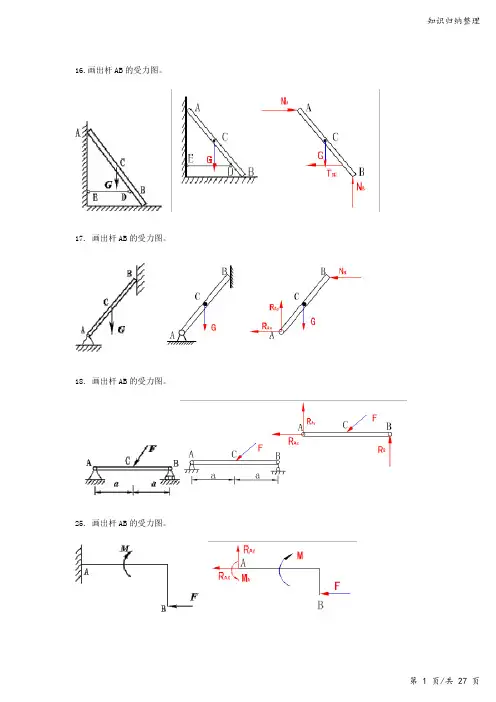
知识归纳整理16.画出杆AB 的受力图。
17. 画出杆AB 的受力图。
18. 画出杆AB的受力图。
25. 画出杆AB 的受力图。
物系受力图26. 画出图示物体系中杆AB、轮C、整体的受力图。
7. 图示圆柱A重力为G，在中心上系有两绳AB和AC，绳子分别绕过光滑的滑轮B和C，并分别悬挂重力为G1和G2的物体，设G2＞G1。
试求平衡时的α角和水平面D对圆柱的约束力。
解（1）取圆柱A画受力图如图所示。
AB、AC绳子拉力大小分别等于G1，G2。
（2）建直角坐标系，列平衡方程：∑Fx ＝0，-G1+G2cosα＝0求知若饥，虚心若愚。
∑F y ＝0， F N ＋G 2sinα-G ＝0 （3）求解未知量。
8.图示翻罐笼由滚轮A，B 支承，已知翻罐笼连同煤车共重G=3kN，α=30°，β=45°，求滚轮A，B 所受到的压力F NA ，F NB 。
有人以为F NA =Gcos α，F NB =Gcos β，对不对，为什么？解（1）取翻罐笼画受力图如图所示。
（2）建直角坐标系，列平衡方程： ∑F x ＝0， F NA sinα-F NB sinβ＝0 ∑F y ＝0， F NA cosα+F NB cosβ-G＝0 （3）求解未知量与讨论。
将已知条件G=3kN，α=30°，β=45°分别代入平衡方程，解得： F NA ＝2.2kN F NA ＝1.55kN有人以为F NA =Gcosα，F NB =Gcosβ是不正确的，惟独在α=β=45°的事情下才正确。
千里之行，始于足下。
9.图示简易起重机用钢丝绳吊起重力G=2kN 的重物，不计杆件自重、摩擦及滑轮大小，A，B，C三处简化为铰链连接；求AB 和AC 所受的力。
解（1）取滑轮画受力图如图所示。
AB、AC 杆均为二力杆。
（2）建直角坐标系如图，列平衡方程：∑F x ＝0， -F AB -Fsin45°+Fcos60°＝0 ∑F y ＝0， -F AC -Fsin60°-Fcos45°＝0 （3）求解未知量。
湖南科技学院第8届大学生物理竞赛答案一、填空题（每空2分，共计30分）1．（︒-30sin g ，︒30cos 2g υ） 2． （J 12）3.（204a qπε，由O 指向D ） 4.（E R 2π，0）5．（平行于x 轴，沿z 轴的反方向）6．（2222-T mA π）7.（氧气，氢气，1T ）8. （h A 0，mv v h )(201-） 二、计算题（共计70分） 1、（12分）解：棒与小球绕轴的转动惯量为3/431222Ml Ml Ml J =+=取棒、球和子弹为系统，在子弹穿过小球时，系统所受外力对轴的合力矩为零，对轴的角动量守恒．设子弹刚穿出小球后，棒的角速度为ω0则有021ωJ l m l m +⋅=v v 由此可解得 ω0＝3m v / 8Ml ①要使棒能转动完整的一周，必须球能摆至最高点，且这时棒的角速度ω ≥0．从最低点到最高点的过程中，棒、球与地球系统的机械能守恒．取球在最低点时重力势能为零，则220212322/21ωωJ l Mg l Mg Mgl J ++⋅=+ ② 由①、②式并利用ω ≥0的条件，可解得子弹的最小入射速率为gl m M24min =v 2、（12分）(1) a r R <<场强：3013π4,π4rr Q E r Qr D ε ==介质内)(b r a <<场强：3023π4,π4rr Q E r r Q D r εε ==; 介质外)(b r >场强：3033π4,π4r r Q E r Qr D ε == 金属球的电势r d r d r d 321 ⋅+⋅+⋅=⎰⎰⎰∞b b a a R E E E U r d 4r d 4r d 433030 ⋅+⋅+⋅=⎰⎰⎰∞b b a r a R r r Q r r Q r r Q πεεπεπε )11(π4)11(π400ba Q a R Q r r -++-=εεεε 3、（12分）解: 计算抛物线与CD 组成的面积内的磁通量⎰⎰=-==aym y B x x y B S B 0232322d )(2d 2ααΦ ∴ v y B t y y B t m 21212d d d d ααε-=-=Φ-= ∵ ay v 22=∴ 212y a v =则 ααεaBy y a y Bi 8222121-=-= i ε实际方向沿ODC ．4、解：(1)等体过程由热力学第一定律得E Q ∆=吸热 )(2)(1212V T T R i T T C E Q -=-=∆=υυ25.623)300350(31.823=-⨯⨯=∆=E Q J对外作功 0=A(2)等压过程)(22)(1212P T T R i T T C Q -+=-=υυ吸热 75.1038)300350(31.825=-⨯⨯=Q J )(12V T T C E -=∆υ内能增加 25.623)300350(31.823=-⨯⨯=∆E J对外作功 5.4155.62375.1038=-=∆-=E Q A J 5、解: 由反射干涉相长公式有λλk ne =+22 ),2,1(⋅⋅⋅=k得 122021612380033.14124-=-⨯⨯=-=k k k ne λ 2=k , 67392=λo A (红色)3=k , 40433=λ o A (紫色)所以肥皂膜正面呈现紫红色．由透射干涉相长公式 λk ne =2),2,1(⋅⋅⋅=k所以 k k ne 101082==λ 当2=k 时， λ =5054o A (绿色)故背面呈现绿色．6、（10分）解：22*)23cos 1(ax a πψψψ== a a a a a a a a 21)21(14cos 1)4(cos 145cos 12653cos 122222===+===πππππ。
力学竞赛试题及答案一、 四叶玫瑰线解：（1）对于四叶玫瑰曲线θρ2cos a =，在直角坐标系中可写成（图3-1）⎩⎨⎧==θρθρsin cos y x 将θρ2cos a =代入上式， 得 ⎩⎨⎧==θθθθsin 2cos cos 2cos a y a x （1） 利用三角函数的积化和差公式 )]cos()[cos(21cos cos βαβαβα-++=)]sin()[sin(21sin cos βαβαβα-++=可得 ⎪⎪⎩⎪⎪⎨⎧-=+=)sin 3(sin 2 )cos 3(cos 2θθθθa y a x （2）图3-1 图3-2（2）现设计一行星齿轮机构来画此曲线。
如图3-2所示的行星齿轮机构，小齿轮1O 在固定内齿轮O 内作纯滚动，其中内齿轮的半径为R ，小齿轮的半径为r ，画笔所在E 点离小齿轮圆心1O 的距离为e 。
随系杆1OO 的转动，其E 点的轨迹为⎩⎨⎧--=+-=ϕθϕθsin sin )( cos cos )( e r R y e r R x EE 利用小齿轮的纯滚动条件)(θϕθ+=r R ，有θϕrrR -=，代入上式可得⎪⎪⎩⎪⎪⎨⎧---=-+-=)sin(sin )( )cos(cos )( ϕθϕθr r R e r R y r r R e r R x E E 作变换，令βϑ3=，上式可改写为⎪⎪⎩⎪⎪⎨⎧---=-+-=)3sin(3sin )( )3cos(3cos )( ϕβϕβr r R e r R y r r R e r R x E E （3）对照式（2）和式（3）中的系数，有2ae =， 2a r R =-， 13=-r r R联解之，得a R 2=， a r 23=， 2ae = （4） 做一个如图3-2所示的行星齿轮绘图机构，取式（4）中的参数，即可画出θρ2cos a =的四叶玫瑰曲线。
二． 手指转笔在你思考问题时有用手指转笔的习惯吗？请你用下述刚体简化模型，进行分析计算： （1）本问题与力学中的什么内容有关系？（2）求出笔绕手指无滑动转一周中，手指作用于笔的正压力和摩擦力的大小； （3）给出笔与手指间的摩擦因数μ随AC 长度x 变化应满足的条件。
力学竞赛大学试题及答案一、选择题（每题5分，共20分）1. 一个物体在水平面上以恒定速度直线运动，其运动状态是：A. 静止B. 匀速直线运动C. 匀速圆周运动D. 变速直线运动答案：B2. 牛顿第二定律的数学表达式是：A. F = maB. F = mvC. F = m(v^2)D. F = m(v^2)/r答案：A3. 根据能量守恒定律，下列说法正确的是：A. 能量可以在不同形式之间转换B. 能量可以在不同物体之间转移C. 能量的总量可以增加D. 能量的总量可以减少答案：A4. 一个物体从静止开始做自由落体运动，其下落高度与时间的关系为：A. h = 1/2gt^2B. h = gtC. h = 2gtD. h = gt^2答案：A二、填空题（每题5分，共20分）1. 根据牛顿第三定律，作用力和反作用力大小________，方向________，作用在________的物体上。
答案：相等；相反；不同2. 一个物体的动能与其质量成正比，与其速度的平方成正比，其公式为：Ek = ________。
答案：1/2mv^23. 一个物体在斜面上下滑时，其受到的摩擦力大小与斜面的倾角成________关系。
答案：正比4. 根据胡克定律，弹簧的弹力与其形变成正比，其公式为：F =________。
答案：kx三、计算题（每题10分，共20分）1. 一辆汽车以20m/s的速度在水平公路上匀速行驶，求汽车受到的摩擦力大小，已知汽车质量为1500kg，摩擦系数为0.05。
答案：汽车受到的摩擦力大小为750N。
2. 一个质量为2kg的物体从10m高处自由落下，忽略空气阻力，求物体落地时的速度。
答案：物体落地时的速度为20m/s。
四、简答题（每题10分，共20分）1. 简述牛顿第一定律的内容及其物理意义。
答案：牛顿第一定律，也称为惯性定律，指出一切物体在没有受到外力作用时，总保持静止状态或匀速直线运动状态。
其物理意义是，物体具有惯性，即物体倾向于保持其当前的运动状态，除非有外力作用。
练习一运动的描述 （一）1．（D ）2.（D ）3．217,5s m s m 4．m m π5,105．（1）s m t x V 5.0-=∆∆= （2）()s m v t t dt dx v 62,692-=-==（3）()()()()质点反向运动时，,05.125.25.1215.1===⨯-⨯+⨯-⨯=v s t m S6．答：矢径是从坐标原点至质点所在位置的有向线段。
位移是由前一时刻质点所在位置引向后一时刻质点所在位置的有向线段，它们的一般关系为r r r ρρρ-=∆若把坐标原点选在质点的初始位置，则00=r ρ，任意时刻质点对此位置的位移为r r ρρ=∆，即此时r ρ既是矢径也是位移。
练习二 运动的描述 （一）1． ()()s m t t s rad t t 612,34223--2．（c ）3．三 ， 三至六4．s m s m s m 20,3103.17=5．1032,224,432102+===∴===⎰⎰⎰⎰t x dt t dx t v tdtdv t dt dv a txv t6．根据已知条件确定常量K222224,4,4Rt R v t s d ra Rt v t k ======ωωω22222228.3532168841s m a a a sm R v a s m Rt dt v d a s m Rt v s t n n =+=========ττ时，练习三 运动定律与力学中的守恒定律（一）1．（D ）2. （C ）3．4．θ2cos 15．因绳子质量不计，所以环受到的摩擦力在数值上等于张力T ，设2m 对地加速度为/2a ，取向上为正；1m 对地加速度为1a （亦即绳子的加速度）向下⎪⎩⎪⎨⎧-==-=-21/2/222111aa a a m g m T a m T g m()()()212121/22121221222112m m a m g m m a m m m m a g T m m a m g m m a +--=+-=++-=解得：6．(1)子弹进入沙土后受力为－kv,由牛顿定律有mt k v v t ev v vdv dt m k vdvdt m k dt dvm kv -=∴=-=-∴=-⎰⎰00,,（2）求最大深度()()kv mv x ev k m x dte v dx dt dx v mkt m kt 00max 00,1,=-=∴=∴=--Θ练习四 运动定律与力学中的守恒定律（二）1．（C ）2.（B ）3．s m S N 24,140⋅()()sm m mv I v mv mv I sN dt t dt F I t t 24,14040301212221=+=∴-=⋅=+==⎰⎰ρΘ4．2221221,m t F m m t F m m tF ∆++∆+∆5．（1）系统在水平方向动量守恒。
这个答案仅供复习之用,平时一定要自己动脑筋做作业…..练习一 运动的描述 （一）1．（D ） 2.（D ）3．217,5s m s m 4．m m π5,105．（1）s m t x V 5.0-=∆∆= （2）()s m v t t dt dx v 62,692-=-==（3）()()()()质点反向运动时，,05.125.25.1215.1===⨯-⨯+⨯-⨯=v s t m S6．答：矢径是从坐标原点至质点所在位置的有向线段。
位移是由前一时刻质点所在位置引向后一时刻质点所在位置的有向线段，它们的一般关系为r r r -=∆若把坐标原点选在质点的初始位置，则00=r，任意时刻质点对此位置的位移为r r =∆，即此时r既是矢径也是位移。
练习二 运动的描述 （一）1． ()()s m t t s rad t t 612,34223--2．（c ）3．三 ， 三至六4．s m s m s m 20,3103.17=5．1032,224,432102+===∴===⎰⎰⎰⎰t x dt t dx t v tdtdv t dt dv a txv t6．根据已知条件确定常量K222224,4,4RtR v t s d ra Rt v t k ======ωωω22222228.3532168841s m a a a sm R v a s m Rt dt v d a s m Rt v s t n n =+=========ττ时，练习三 运动定律与力学中的守恒定律（一）1．（D ）2. （C ）3．4．θ2cos 15．因绳子质量不计，所以环受到的摩擦力在数值上等于张力T ，设2m 对地加速度为/2a ，取向上为正；1m 对地加速度为1a （亦即绳子的加速度）向下⎪⎩⎪⎨⎧-==-=-21/2/222111aa a a m g m T a m T g m()()()212121/22121221222112m m a m g m m a m m m m a g T m m a m g m m a +--=+-=++-=解得：6．(1)子弹进入沙土后受力为－kv,由牛顿定律有mt k v v t ev v vdv dt m k vdvdt m k dt dvm kv -=∴=-=-∴=-⎰⎰00,,TT()相对2a 2()牵连1a（2）求最大深度()()kv m x ev k m x dte v dx dt dx v kt m kt 0max 00,1,=-=∴=∴=--练习四 运动定律与力学中的守恒定律（二）1．（C ）2.（B ）3．s m S N 24,140⋅()()sm m mv I v mv mv I sN dt t dt F I t t 24,14040301212221=+=∴-=⋅=+==⎰⎰4．22211211,m t F m m t F m m t F ∆++∆+∆5．（1）系统在水平方向动量守恒。
力学竞赛练习一、选择题1.如下列图，均匀细杆AB 质量为M ，A 端装有转轴，B 端连接细线通过滑轮和质量为m 的重物C 相连，假设杆AB 呈水平，细线与水平方向夹角为θ时恰能保持平衡，则杆对轴A 有作用力大小下面表达式中不正确的选项是〔 〕 A.mgB ．Mg2 sin θC ．M 2－2Mm sin θ＋m 2 gD ．Mg －mg sin θ2．如下列图，在倾角为θ的光滑斜面上A 点处，以初速v 0与斜面成α角斜抛出一小球，小球落下将与斜面作弹性碰撞．求a θ、满足什么条件时，小球将逐点返跳回出发点A ？( )．A ．k =⋅θαcos sinB ．k =⋅θαsin cosC ．k =⋅θαcot cotD ．k =θαtan tan (123=,,,k )3.在竖直平面的一段光滑圆弧轨道上有等高的两点M 、N ，它们所对圆心角小于10°，P 点是圆弧的最低点，Q 为弧NP 上的一点，在QP 间搭一光滑斜面，将两小滑块〔可视为质点〕分别同时从Q 点和M 点由静止释放，则两小滑块的相遇点一定在〔 〕 （A ）P 点 〔B 〕斜面PQ 上的一点〔C 〕PM 弧上的一点 〔D 〕滑块质量较大的那一侧4.一木板坚直地立在车上，车在雨中匀速进展一段给定的路程。
木板板面与车前进方向垂直，其厚度可忽略。
设空间单位体积中的雨点数目处处相等，雨点匀速坚直下落。
以下诸因素中与落在木板面上雨点的数量有关的因素是〔 〕A B θ CA 、雨点下落的速度B 、单位体积中的雨点数C 、车行进的速度D 、木板的面积5.有一只小虫清晨6时起从地面沿树干向上爬，爬到树顶时是下午6时，第二天清晨6时起从树顶沿树干向下爬，爬回地面时是下午四时。
假设小虫爬行时快时慢，则两天中，一样钟点〔时、分、秒〕爬过树干上一样高度的时机是〔 〕 A ．一定有一次 B.可能没有 C ．可能有两次 D.一定没有6.物体A 、B 质量一样，在倾角为30o 的光滑斜面上，滑轮及绳子质量均不计，下滑轮通过轻杆固定在斜面底端，现将系统由静止释放，则物体A 在下降h 距离时的速度大小为〔 〕 A ． 2 g h B ．2 3 g h ／5 C ．22gh D ．8 g h ／57.如下列图，在静止的杯中盛水，弹簧下端固定在杯底，上端系一密度小于水的木球．当杯自由下落时，弹簧稳定时的长度将( )． A ．变长 B ．恢复到原长 C ．不变 D ．无法确定8.如下列图，M 、N 是两个共轴圆筒的横截面．外筒半径为R ，筒半径比R 小得多，可以忽略不计．筒的两端是封闭的，两筒之间抽成真空．两筒以一样的角速度ω绕其中心轴线(图中垂直于纸面)匀速转动．设从M 筒部可以通过窄缝S(与M 筒的轴线平行)不断地向外射出，两种不同速率v1和v2的微粒，从S 处射出时初速度方向都是沿筒的半径方向，微粒到达N 筒后就附着在N 筒上．如果R 、v1和v2都不变，而ω取*一适宜的值，则( )A ．有可能使微粒落在N 筒上的位置都在a 处一条与S 缝平行的窄条上B ．有可能使微粒落在N 筒上的位置都在*一处如b 处一条与S 缝平行的窄条上C ．有可能使微粒落在N 筒上的位置分别在*两处如b 处和c 处与S 缝平行的窄条上BA30D ．只要时间足够长，N 筒上将到处落有微粒 量为二、填空题1.一均匀的不可伸长的绳子，其两端悬挂在A 、B 两点，B 点比A 点高h ．在A 点，绳子力为T A ．绳子的质m ，绳长为L ．则在B 点绳子的力T B =.2.质量为m 的小球挂在长为L 、不可伸长的轻线上，静止于自然悬挂状态。
湖南科技学院第8届大学生物理竞赛试卷时间：120分钟 满分100分一、填空题（每空2分，共计30分）1．一物体作如图所示的斜抛运动，测得在轨道Ｐ点处速度大小为v ，其方向与水平方向成30°角。
则物体在Ｐ点的切向加速度a τ= ，轨道的曲率半径ρ= 。
2． 一质点在二恒力的作用下，位移为△r=3i +8j（m ），在此过程中，动能增量为24J ，已知其中一恒力1F =12i -3j（N ），则另一恒力所作的功为 。
3． 如图所示，边长分别为a 和b 的矩形，其A 、B 、C 三个顶点上分别放置三个电量均为q 的点电荷，则中心O 点的场强为 方向 。
4. 在场强为E 的均匀电场中取一半球面，其半径为R ，电场强度的方向与半球面的对称轴平行。
则通过这个半球面的电通量为 ，若用半径为R 的圆面将半球面封闭，则通过这个封闭的半球面的电通量为 。
5．如图所示，正电荷q 在磁场中运动，速度沿x 轴正方向。
若电荷q 不受力，则外磁场B的方向是__________；若电荷q 受到沿y 轴正方向的力，且受到的力为最大值，则外磁场的方向为__________。
6．质量为m 的物体和一轻弹簧组成弹簧振子其固有振动周期为T ，当它作振幅为A 的自由简谐振动时，其振动能量E = 。
7. 同一温度下的氢气和氧气的速率分布曲线如右图所示，其中曲线1为_____________的速率分布曲线，__________的最概然速率较大（填“氢气”或“氧气”）。
若图中曲线表示同一种气体不同温度时的速率分布曲线，温度分别为T 1和T 2且T 1<T 2；则曲线1代表温度为________的分布曲线（填T 1或T 2）。
8. 已知某金属的逸出功为0A ，用频率为1γ光照射使金属产生光电效应，则， （1）该金属的红限频率0γ=____________；（2）光电子的最大速度v =___________。
B二、计算题（第1到第5题，每题12分，第6题10分，共计70分）1、（12）有一质量为M 、长度为l 的均匀细棒，其一端固结一个质量也为M 的小球，可绕通过另一端且垂直于细棒的水平光滑固定轴自由转动．最初棒自然下垂．现有一质量为m 的子弹，在垂直于轴的平面内以水平速度v射穿小球，子弹穿过小球时速率减为v 21，要使棒能绕轴作完整的一周转动，子弹入射时的速率至少必须为多大？2、 （12分）半径为R 的金属球带电荷Q ，球外套一个同心球壳的均匀电介质，其内外半径分别为a 和b ，相对介电常数为r ε（如图所示）。
湘潭大学2012年上学期 《大学物理I (1)、II (1)》课程考试试卷一、选择题（10个小题，每小题3分，共30分）1.质量分别为m 1和m 2的两滑块A 和B 通过一轻弹簧水平连结后置于水平桌面上，滑块与桌面间的摩擦系数均为μ，系统在水平拉力F 作用下匀速运动，如图所示．如突然撤消拉力，则刚撤消后瞬间，二者的加速度a A 和a B 分别为［］(A) a A =0,a B =0. (B) a A >0,a B <0.(C) a A <0,a B >0. (D) a A <0,a B =0.2.人造地球卫星，绕地球作椭圆轨道运动，地球在椭圆的一个焦点上，则卫星的 (A)动量不守恒，动能守恒． (B)动量守恒，动能不守恒．(C)对地心的角动量守恒，动能不守恒． (D)对地心的角动量不守恒，动能守恒．［］3．一辆汽车从静止出发在平直公路上加速前进．如果发动机的功率一定，下面哪一种说法是正确的？(A) 汽车的加速度是不变的． (B) 汽车的加速度随时间减小．(C) 汽车的加速度与它的速度成正比． (D) 汽车的速度与它通过的路程成正比． (E) 汽车的动能与它通过的路程成正比．［］4．在恒定不变的压强下，气体分子的平均碰撞频率Z 与气体的热力学温度T 的关系为 (A) Z 与T 无关．(B) Z 与T 成正比．(C) Z 与T 成反比．(D) Z 与T 成正比． [ ］5.一定量的气体作绝热自由膨胀，设其内能增量为∆E ，熵增量为∆S ，则应有： (A) ∆E < 0，∆S = 0． (B) ∆E < 0，∆S > 0．(C) ∆E = 0，∆S > 0． (D) ∆E = 0，∆S = 0．［］6.图中所示曲线表示球对称或轴对称静电场的某一物理量随径向距离r 变化的关系，请指出该曲线可描述下列哪方面内容(E 为电场强度的大小，U 为电势）[ ](A)半径为R 的无限长均匀带电圆柱体电场的E ~r 关系．(B)半径为R 的无限长均匀带电圆柱面电场的E ~r 关系． (C)半径为R 的均匀带正电球体电场的U ~r 关系．(D) 半径为R 的均匀带正电球面电场的U ~r 关系．7.点电荷Q 被曲面S 所包围，从无穷远处引入另一点电荷q 至曲面外一点，如图所示， 则引入前后：［］(A)曲面S 的电场强度通量不变，曲面上各点场强不变． (B) 曲面S 的电场强度通量变化，曲面上各点场强不变． (C) 曲面S 的电场强度通量变化，曲面上各点场强变化．(D) 曲面S 的电场强度通量不变，曲面上各点场强变化．8.已知某简谐振动的振动曲线如图所示，位移的单位为厘M ，时间单位为秒．则此简谐振动的振动方程为： [ ](A) )3232cos(2π+π=t x ．(B) )3232cos(2π-π=t x ．(C) )3234cos(2π+π=t x ．(D))3234cos(2π-π=t x ．(E) )4134cos(2π-π=t x ．9.一质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是 (A) 4f . (B) 2f . (C) f .(D) 2/f . (E) f /4 ［］10.设某微观粒子的总能量是它的静止能量的K 倍，则其运动速度的大小为(以c 表示真空中的光速)(A)1-K c ． (B) 21K K c -． (C) 12-K K c ． (D) )2(1++K K K c．［］ 二、填空题（9个小题, 共29分）11. ( 4分)一质点沿半径为 0.1 m 的圆周运动，其角位移θ 随时间t 的变化规律是θ= 2 + 4t 2 (SI)．在t =2 s 时，它的法向加速度a n =______________；切向加速度a t =________________． 12. ( 4分)一块水平木板上放一砝码，砝码的质量m ＝0.2 kg ，手扶木板保持水平，托着砝码使之在竖直平面内做半径R ＝0.5 m运动，速率υ=1 m/s 的摩擦力为_____________，砝码受到木板的支持力为13. ( 3分)一人站在质量（连人带船）为m 1＝300 kg 的静止的船上，他用F ＝100 N 的恒力拉一水平轻绳，绳的另一端系在岸边的一棵树上，则船开始运动后第三秒末的速率为____________；在这段时间内拉力对船所做的功为________________．（水的阻力不计） 14. (3分) 一个质量为m 的小虫，在有光滑竖直固定中心轴的水平圆盘边缘上，沿逆时针方向爬行，它相对于地面的速率为υ，此时圆盘正沿顺时针方向转动，相对于地面的角速度为ω .设圆盘对中心轴的转动惯量为J ．若小虫停止爬行，则圆盘的角速度为_______________。
