第四届湖南省大学生力学竞赛试题(材料力学答案)

湖南省⼤学⽣物理竞赛试卷及答案湖南省第4届⼤学⽣物理竞赛试卷2011年5⽉14⽇时间：150分钟满分120分⼀、选择题 (每题3分，共18分)1.设某种⽓体的分⼦速率分布函数为，则速率在～内的分⼦的平均速率为（）。

(A) ； (B) ；(C) ； (D) 。

2. 如图所⽰带负电的粒⼦束垂直地射⼊两磁铁之间的⽔平磁场，则( )。

(A) 粒⼦向极移动；(B) 粒⼦向极移动；(C) 粒⼦向下偏转；(D) 粒⼦向上偏转。

3.如图所⽰，⼀个带电量为的点电荷位于⽴⽅体的⾓上，则通过侧⾯的电场强度通量等于（）。

A、； B 、；C、； D 、。

4. 如图所⽰, ⼀光学平板玻璃 A 与待测元件 B 之间形成空⽓劈尖，⽤波长的单⾊光垂直照射，看到的反射光的⼲涉条纹如图所⽰，有些条纹弯曲部分的顶点恰好于其右边条纹的直线部分的切线相切，则⼯件的上表⾯缺陷是 ( ) 。

（A）不平处为凸起纹，最⼤⾼度为；（B）不平处为凸起纹，最⼤⾼度为；（C）不平处为凹槽，最⼤⾼度为；Aq cbda（D）不平处为凹槽，最⼤⾼度为。

5. 在图⽰三种透明材料构成的⽜顿环装置中，⽤单⾊光垂直照射，在反射光中看到⼲涉条纹，则在接触点P处形成的圆斑为( ) 。

(A) 全明； (B) 全暗；(C) 右半部明，左半部暗； (D) 右半部暗，左半部明。

6. 已知粒⼦在⼀维矩形⽆限深势阱中运动，其波函数为：那么粒⼦在处出现的⼏率密度为（）。

(A) ； (B) ； (C) ； (D) 。

⼆、填空题(每题3分，共21分)1. ⼀匀质细杆长为，质量为，杆两端⽤线吊起，保持⽔平，现有⼀条线突然断开，则断开瞬间另⼀条线的张⼒为。

2. 图⽰两条曲线分别表⽰氦、氧两种⽓体在相同温度时分⼦按速率的分布，其中曲线 1 表⽰ _ _⽓分⼦的速率分布曲线，曲线 2 表⽰ __ _ ⽓分⼦的速率分布曲线。

3. ⼀氧⽓瓶的容积为，充⼊氧⽓的压强为，⽤了⼀段时间后压强降为，则瓶中剩下的氧⽓的内能与未⽤前氧⽓的内能之⽐为。

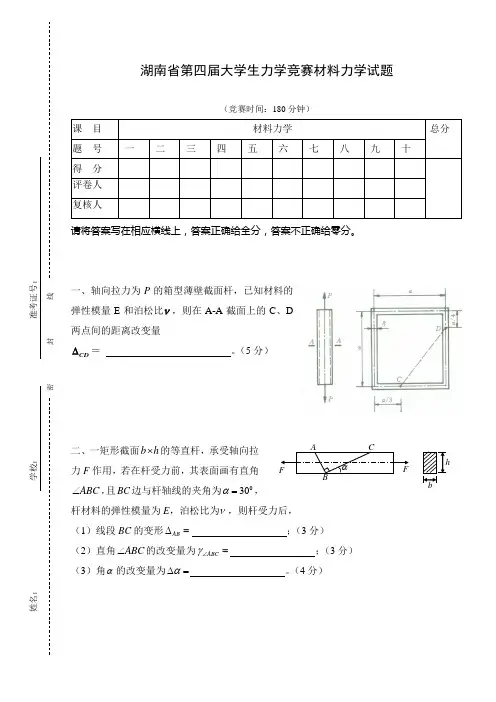
湖南省第四届大学生力学竞赛材料力学试题（竞赛时间：180分钟）课 目 材料力学 总分题 号 一二三四五六七八九十得 分评卷人 复核人请将答案写在相应横线上，答案正确给全分，答案不正确给零分。

一、轴向拉力为P 的箱型薄壁截面杆，已知材料的弹性模量E 和泊松比ν，则在A-A 截面上的C 、D 两点间的距离改变量CD ∆＝ 。

（5分）二、一矩形截面b h ⨯的等直杆，承受轴向拉力F 作用，若在杆受力前，其表面画有直角ABC ∠，且BC 边与杆轴线的夹角为030α=，杆材料的弹性模量为E ，泊松比为ν，则杆受力后， （1）线段BC 的变形AB ∆= ；（3分） （2）直角ABC ∠的改变量为ABC γ∠= ；（3分） （3）角α的改变量为α∆= 。

（4分）姓名： 学校： 准考证号：bhFABFCα密 封 线三、图示杆（不考虑自重）下端与固定端约束距离为∆。

在中点受到静力F 作用，在线弹性范围内，力的作用点的最终位移为δ。

那么，在以下三种情况下，计算杆所储存的应变能V ε。

（结果请用c 、δ和∆表示，其中c=EA/l ，EA 为杆的拉压刚度）。

（1）∆=0时，V ε = ；（4分） （2）∆≠0且δ<∆时， V ε = ；（3分） （3）∆≠0且δ>∆时，V ε = 。

（5分）四、已知四分之一的圆截面对形心c z 轴的惯性矩()25624-=πd I zc ，则截面对形心c y 轴的惯性矩ycI ＝ 。

（5分）五、图示三根圆钢具有相同的长度l 与直径d ，材料的弹性模量与切变模量为E 与G ，一端固定于刚性固定平面N 1之上，呈等边三角形，各边长为a ，另一端固联于与N 1平行的刚性平面N 2上，如在平面内作用一力偶M k ，则（1）当直径d 较大而长度l 较小时，略去弯曲效应的影响，平面N 2的转角θ = ；（5分）（2）当直径d<<l 时，平面N 2的转角θ = 。

（6分）六、图示梁AB左端固定，右端自由，在其中点D连接一长度为a的拉杆CD，自由端下方竖直放置刚度系数为k的弹簧，弹簧顶端与梁自由端有一微小间隙 。

材料力学基础测试题(含答案)材料力学基础测试题（1至6章）一、判断题：（对“√”，错“X”各1分共10分）1、E的大小与杆的材料和长度无关。

（X）2、求超静定问题时要由几何关系和物理关系建立补充方程。

（√）3、胡克定理的适用条件是ρσσ≤对吗？（√）4、提高梁的强度主要是改变L和E。

（X）5、一般细长梁弯曲正应力强度满足则剪应力强度必满足。

（√）6、图示结构为2次超静定桁架。

（X）7、图示直梁在截面C承受eM作用。

则截面C转角不为零，挠度为零。

（√）8、等直传动轴如图所示，轮B和轮D为主动轮，轮A，轮C和轮E为从动轮。

若主动轮B和D上的输入功率相等，从动轮A,C 和E上的输出功率也相等，如只考虑扭转变形而不考虑弯曲变形，危险截面的位置在AB区间和DEA M e C l/2B区间。

（√）9截面面积为10变形。

（X1、234边界条件是A C5、低碳钢拉拉伸实验中四个阶段是：（1）（2）（3）（4）6、一般基本变形中，强度条件可解的三类问题是：。

7、已知图（a）梁B端挠度为q4l/(8E I)，转角为q3l/（6E I），则图（b）梁C截面的转角为。

8、当L/h＞的梁为细长梁。

三、选择题：（各2分，共28分）1、任意截面形状的等直梁在弹性纯弯曲条件下，中性轴的位置问题有四种答案：(A)等分横截面积；(B)通过横截面的形心；(C)通过横截面的弯心；(D)由横截面上拉力对中性轴的力矩等于压力对该轴的力矩的条件确定。

正确答案是B。

2、一梁拟用图示两种方法搁置，则两种情况下的最大正应力之比max amax b()()σσ为：lF(a)(A)14；(B)116；(C)164；(D)16。

正确答案是A。

3、甲和乙两杆，几何尺寸相同，轴向拉力F相同，材料不同，它们的应力和变形可能是：(A)应力σ和变形l?都相同；(B)应力σ不同，变形l?相同；(C)应力σ相同，变形l?不同(D)应力σ不同，变形l?不同。

正确答案是。

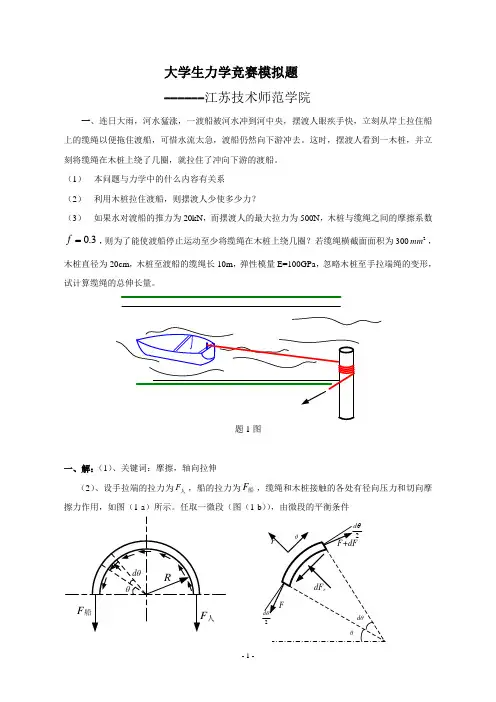
大学生力学竞赛模拟题 ------江苏技术师范学院一、连日大雨，河水猛涨，一渡船被河水冲到河中央，摆渡人眼疾手快，立刻从岸上拉住船上的缆绳以便拖住渡船，可惜水流太急，渡船仍然向下游冲去。

这时，摆渡人看到一木桩，并立刻将缆绳在木桩上绕了几圈，就拉住了冲向下游的渡船。

（1） 本问题与力学中的什么内容有关系 （2） 利用木桩拉住渡船，则摆渡人少使多少力？（3） 如果水对渡船的推力为20kN ，而摆渡人的最大拉力为500N ，木桩与缆绳之间的摩擦系数3.0=f ，则为了能使渡船停止运动至少将缆绳在木桩上绕几圈？若缆绳横截面面积为3002mm ，木桩直径为20cm ，木桩至渡船的缆绳长10m ，弹性模量E=100GPa ，忽略木桩至手拉端绳的变形，试计算缆绳的总伸长量。

题1图一、解：（1）、关键词：摩擦，轴向拉伸（2）、设手拉端的拉力为人F ，船的拉力为船F ，缆绳和木桩接触的各处有径向压力和切向摩擦力作用，如图（1-a ）所示。

任取一微段（图（1-b ）），由微段的平衡条件（1-a ） （1-b ）0=∑r F 02sin 2sin )(=-+-θθd F d dF F dF r （1） 0=∑θF ()02cos 2cos=--+r fdF d F d dF F θθ （2） 对于微小角度θd ，可令 22sinθθd d ≈，12cos ≈θd ，并略去高阶微量2θd dF ⨯，即得fF d dF=θ（3） 分离变量，积分得θf Ae F = （4）其中积分常数由缆绳两端的边界条件确定，有0=θ， 船F F =； 船F A =所以，绕在木桩上缆绳任一截面的拉力为θf e F F 船= （5）所以θf e F F =船人，其中θ为缆绳绕过木桩的角度。

（3）、将N F 500=人，kN F 20=船，f = 0.3代入式（5），得θ3.031020500e ⨯=解得 3.12≈θ rad 所以至少将缆绳绕两圈。

练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4）应力是内力分布集度。

（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6）若物体产生位移，则必定同时产生变形。

（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。

（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。

（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。

（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。

（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。

变形。

（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。

（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。

1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。

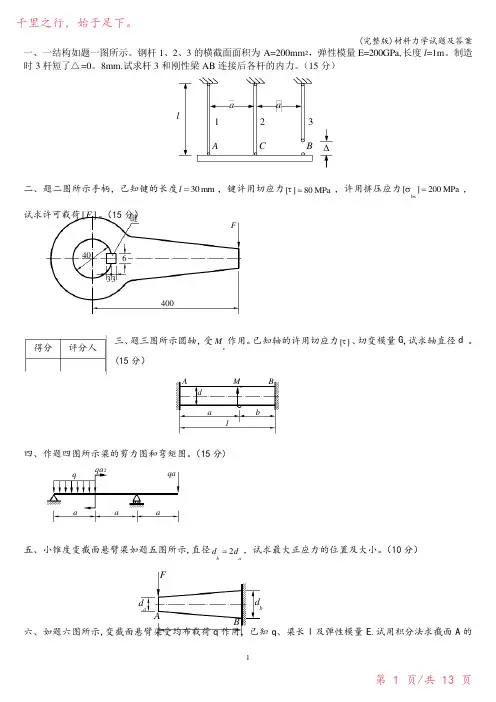
一、一结构如题一图所示。

钢杆1、2、3的横截面面积为A=200mm 2，弹性模量E=200GPa,长度l =1m 。

制造时3杆短了△=0。

8mm.试求杆3和刚性梁AB 连接后各杆的内力。

（15分）aalABC123∆二、题二图所示手柄，已知键的长度30 mm l =，键许用切应力[]80 MPa τ=，许用挤压应力bs[]200 MPa σ=，试求许可载荷][F 。

（15分）三、题三图所示圆轴，受eM 作用。

已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。

(15分）四、作题四图所示梁的剪力图和弯矩图。

（15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =，试求最大正应力的位置及大小。

（10分）六、如题六图所示,变截面悬臂梁受均布载荷q 作用，已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .（15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4，求固定端截面翼缘和腹板交界处点a 的主应力和主方向。

（15分）一、（15分)（1）静力分析（如图（a）)1N F2N F3N F图(a)∑=+=231,0N N N yF F F F（a)∑==31,0N N CF F M(b)（2）几何分析（如图（b)）1l∆2l∆3l∆∆图（b）wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3）物理条件EA l F l N 11=∆，EA l F l N 22=∆，EAl F l N 33=∆ （4）补充方程∆=++EAlF EA l F EA l F N N N 3212 （c） （5）联立（a）、（b）、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分）以手柄和半个键为隔离体，S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体，bsS20F F F ==由剪切：S []s FA ττ=≤，720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、（15分）eABM M M +=0ABϕ=， A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+；当b a >时 e316π ()[]M bd a b τ≥+。

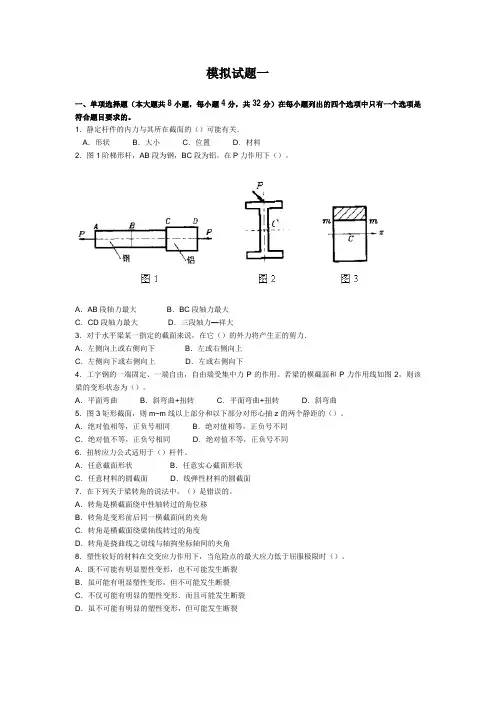
模拟试题一一、单项选择题（本大题共8小题，每小题4分，共32分）在每小题列出的四个选项中只有一个选项是符合题目要求的。

1．静定杆件的内力与其所在截面的（）可能有关．A．形状B．大小C．位置D．材料2．图1阶梯形杆，AB段为钢，BC段为铝。

在P力作用下（）。

A．AB段轴力最大B．BC段轴力最大C．CD段轴力最大D．三段轴力—祥大3．对于水平梁某一指定的截面来说，在它（）的外力将产生正的剪力．A．左侧向上或右侧向下B．左或右侧向上C．左侧向下或右侧向上D．左或右侧向下4．工字钢的一端固定、一端自由，自由端受集中力P的作用。

若梁的横截面和P力作用线如图2，则该梁的变形状态为（）。

A．平面弯曲B．斜弯曲+扭转C．平面弯曲+扭转D．斜弯曲5．图3矩形截面，则m~m线以上部分和以下部分对形心抽z的两个静距的（）。

A．绝对值相等，正负号相同B．绝对值相等，正负号不同C．绝对值不等，正负号相同D．绝对值不等，正负号不同6．扭转应力公式适用于（）杆件。

A．任意截面形状B．任意实心截面形状C．任意材料的圆截面D．线弹性材料的圆截面7．在下列关于梁转角的说法中，（）是错误的。

A．转角是横截面绕中性轴转过的角位移B．转角是变形前后同一横截面间的夹角C．转角是横截面绕梁轴线转过的角度D．转角是挠曲线之切线与轴拘坐标轴间的夹角8．塑性较好的材料在交变应力作用下，当危险点的最大应力低于屈服极限时（）。

A．既不可能有明显塑性变形，也不可能发生断裂B．虽可能有明显塑性变形，但不可能发生断裂C．不仅可能有明显的塑性变形．而且可能发生断裂D．虽不可能有明显的塑性变形，但可能发生断裂二、作图题（本大题共3小题，每小题6分，共18分）。

1．绘图4结构的轴力图。

图42．绘图5结构的扭矩图。

（Te=4kN·m；t=2kN/m；l=2m）图53．绘图6桁梁组合结构中梁式杆的M图。

图6三、计算题（本大题共3小题，第1题15分，第2题15分，第3题20分，共50分）。