江苏省连云港市灌云县四队中学高中数学 向量共线定理教案 苏教版必修4

四队中学教案纸 （学科： 高一数学 ）备课时间教学 课题教时计划1教学课时1教学 目标 1．理解向量加法的概念及向量加法的几何意义； 2．熟练掌握向量加法的平行四边形法则和三角形法则，会作已知两向量的和向量； 3．理解向0量的加法交换律和结合律，并能熟练地运用它们进行向量计算。

重点难点1．如何作两向量的和向量2．向量加法定义的理解教学过程（一）复习：1．向量的概念、表示法。

2．平行向量、相等向量的概念。

3．已知O 点是正六边形ABCDEF 的中心，则下列向量组中含有相等向量的是（ ）（A ）OB uuu r 、CD uuu r 、FE u u u r 、CB u u u r （B ）AB u u u r 、CD uuu r 、FA u u u r 、DE u u u r（C ）FE u u u r 、AB u u u r 、CB u u u r 、OF u u u r （D ）AF u u u r 、AB u u u r 、OC u u ur 、OD u u u r（二）新课讲解：1．向量的加法：求两个向量和的运算叫做向量的加法。

表示：AB BC AC +=u u u r u u u r u u u r．规定：零向量与任一向量a r ，都有00a a a +=+=r r r r r．说明：①共线向量的加法： a r b r a b +r r②不共线向量的加法：如图（1），已知向量a r ，b r，求作向量a b +r r .作法：在平面内任取一点O （如图（2）），作OA a =u u u r r ，AB b =r r ，则OB a b =+u u u r r r.（1） （2）2．向量加法的法则：（1）三角形法则：根据向量加法定义得到的求向量和的方法，称为向量加法的三角形法则。

表示：AB BC AC +=u u u r u u u r u u u r．（2）平行四边形法则：以同一点A 为起点的两个已知向量a r ，b r为邻边作ABCD Y，则则以A 为起点的对角线AC u u u r 就是a r 与b r的和，这种求向量和的方法称为向量加法的平行 四边形法则。

1e 2e aPOA'P'B'C'BA C四队中学教案纸备课时间教学课题 教时 计划1教学课时 1教学 目标 1．掌握及其推论，理解空间任意一个向量可以用不共面的三个已知向量线性表示，而且这种表示是唯一的；2．在简单问题中，会选择适当的基底来表示任一空间向量。

重点难点教学重点：空间向量的基本定理及其推论 教学难点：空间向量的基本定理唯一性的理解教学过程一、创设情景平面向量基本定理的内容及其理解如果21,e e是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a，有且只有一对实数21, ， 使a r2211e e 二、建构数学1、空间向量的基本定理如果三个向量321,,e e e 不共面，那么对空间任一向量p r，存在一个唯一的有序实数组),,(z y x ，使321e z e y e x p证明：（存在性）设321,,e e e 不共面， 过点O 作p OP e OC e OB e OA ,,,321过点P 作直线PP 平行于OC ，交平面OAB 于点P ；在平面OAB 内，过点P 作直线//,//P A OB P B OA ，分别与直线,OA OB 相交于点,A B ，于是，存在三个实数,,x y z ，使3/2/1/,,e z OC OC e y OB OB e x OA OA∴OP OA OB OC xOA yOB zOC u u u r u u u r u u u u r u u u u r u u u r u u u r u u u r所以321e z e y e x p。

四队中学教案纸 （学科： 高一数学 ）备课时间教学课题坐标运算（1）教时计划 2教学课时1教学 目标 1．理解向量的坐标表示法,掌握平面向量与一对有序实数一一对应关系； 2．能正确地用坐标表示向量；3．掌握向量的和、差、数乘的坐标表示法。

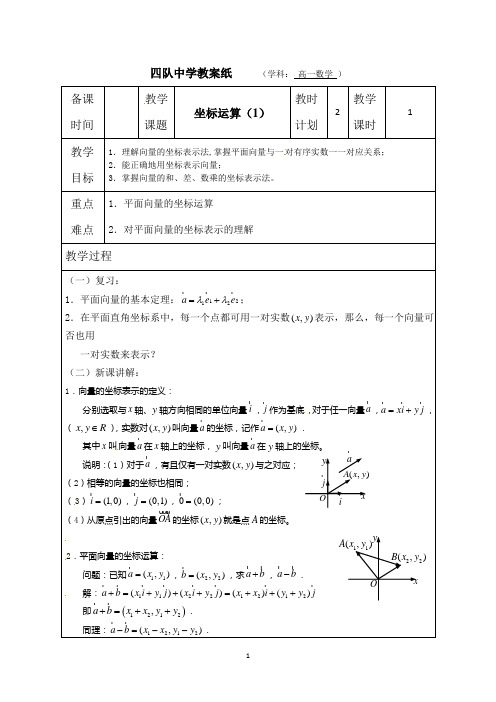
重点难点1．平面向量的坐标运算2．对平面向量的坐标表示的理解教学过程（一）复习：1．平面向量的基本定理：1212a e e λλ=+；2．在平面直角坐标系中，每一个点都可用一对实数(,)x y 表示，那么，每一个向量可否也用一对实数来表示？ （二）新课讲解：1．向量的坐标表示的定义：分别选取与x 轴、y 轴方向相同的单位向量i ，j作为基底，对于任一向量a ，a xi y j =+ ，（,x y R ∈），实数对(,)x y 叫向量a 的坐标，记作(,)a x y =．其中x 叫向量a 在x 轴上的坐标，y 叫向量a在y 轴上的坐标。

说明：（1）对于a ，有且仅有一对实数(,)x y 与之对应；（2）相等的向量的坐标也相同；（3）(1,0)i = ，(0,1)j = ，0(0,0)= ； （4）从原点引出的向量OA的坐标(,)x y 就是点A 的坐标。

2．平面向量的坐标运算：问题：已知11(,)a x y = ，22(,)b x y =，求a b + ，a b - ．解：11221212()()()()a b x i y j x i y j x x i y y j +=+++=+++即()1212,a b x x y y +=++．同理：1212(,)a b x x y y -=--．Ox22(,)B x y11(,)A x yyy x O (,)A x yj ia结论：两个向量和与差的坐标分别等于这两个向量相应坐标的和与差。

3．向量的坐标计算公式：已知向量AB ，且点11(,)A x y ，22(,)B x y ，求AB的坐标．2211(,)(,)AB OB OA x y x y =-=-2121(,)x x y y =--．归纳：（1）一个向量的坐标等于表示它的有向线段的终点坐标减去始点坐标； （2）两个向量相等的充要条件是这二个向量的坐标相等。

F 1
F 2 F 3
a
C'
B'
A'
D'D
A
B
C 四队中学教案纸 （备课人： 学科： ）
备课
时间
教学 课题
教时 计划
1
教学
课时
1
教学 目标 1．运用类比方法，经历向量及其运算由平面向空间推广的过程； 2．了解空间向量的概念，掌握空间向量的线性运算及其性质； 3．理解空间向量共线的充要条件
重点难点 教学重点：空间向量的概念、空间向量的线性运算及其性质；
教学难点：空间向量的线性运算及其性质
教学过程
一、创设情景
1、平面向量的概念及其运算法则；
2、物体的受力情况分析 二、建构数学
1．空间向量的概念：
在空间，我们把具有大小和方向的量叫做向量 注：⑴空间的一个平移就是一个向量
⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量 ⑶空间的两个向量可用同一平面内的两条有向线段来表示 2．空间向量的运算
定义：与平面向量运算一样，空间向量的加法、减法与数乘向量运算如下（如图）
b a AB OA OB
b a OB OA BA
)(R a OP
运算律：
⑴加法交换律：a b b a
⑵加法结合律：)()(c b a c b a
⑶数乘分配律：b a b a
)(
3．共线向量
与平面向量一样，如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫
C B A
O
b b b
a
a。

江苏省连云港市灌云县四队中学高中数学必修四教案：2.2.3 向量的数乘
如图：OB a =+2a =，(()CE a a =--2a =-．
．实数与向量的积的定义：
一般地，实数λ与向量a 的积是一个向量，记作a λ，它的长度与方向规定如下：的方向与a 的方向相同；当0λ<时，a λ的方向与λ时，0a λ=．
．实数与向量的积的运算律：
（结合律）；
a μ（第一分配律）a
b λλ+a+b ）=（第二分配律）
计算：（1）(3)4a -⨯； （2）3(解：（1）原式=12a -； （2．向量共线的充要条件：
（向量共线的充要条件）向量与非零向量a 共线的充要条件是有且只有一个实数与AE 共线．
E B A C
D
12a e e =+，1222b e e =-，且1e ，2e 解：（1）当0a =时，则0b =，显然b 与当0a ≠时， 12121121(4)10454
b e e e e =-=-=中至少有一个为零向量时，显然b 与a 共线．1e ，2e 均不为零向量时，设12e e λ= 2(1)a e λ=+，b 1λ=-时，，a 与a 共线． 1λ≠-时，221b a λλ-=+， 设12,e e 是两个不共线的向量，已知解：))34BD CD e e e e =-+=- 即是12122(4)e ke e e λ+=-. 4k λλ
=-⎩ ，∴k =-，求证A ，B ，三点共线。

平面向量复习与小结灌云县陡沟中学顾继勇教学目标：1．进一步了解平面向量的根本定理及其几何意义，掌握平面向量的分解及其坐标表示，掌握平面向量的坐标运算，理解向量共线的坐标表示；2．进一步理解平面向量数量积的概念及其几何意义，掌握平面向量数量积的坐标表示，并会简单应用；3．进一步掌握将物理问题、实际问题转化为数学问题．教学重点：1．向量共线定理的应用；2．向量根本定理的应用；3．向量的数量积及其坐标表示的应用．教学难点：1．如何将结论和条件建立联系，如何利用图形将未知向量关系转化为向量关系；2．如何利用向量知识解决物理问题及平面几何问题．教学方法：启发教学，谈话式教学相结合．教学过程：2．知识梳理：〔1〕向量是指既有、又有的量，向量的模是指向量的；零向量是指的向量，方向；单位向量是指的向量；〔2〕向量共线定理：；〔3〕平面向量的根本定理：．〔4〕假设A1，1 ，B2，2，那么= ，||= ．〔5〕向量与的夹角为，那么= ．二、学生活动1．命题：①假设≠，且·=·，那么=；②假设=，那么3＜4；③··=··, 对任意向量，，都成立；④2·2=·2；其中正确命题的个数为____ ；2．设，，，用，作基底可将表示，那么实数= ，q= ；3．=〔1，1〕，=〔0，－2〕当= 时, 与共线；4．假设，，且，那么向量与的夹角为．三、数学应用例1 ∣a∣=2，︳b ︳=2，且 a●b=-1﹙1﹚求 a与 b的夹角﹙2﹚求﹙ a-2b﹚●b﹙3﹚当为何值时，向量 ab与向量a-3b 互相垂直例2 〔1〕在ΔABC中，设，，假设，，试以向量、为基底表示向量．〔2〕O为△ABC所在平面内的一点，且满足，试判断△ABC的形状．例3 〔1B〔2〕向量＝1，2，＝–2，–4，||=，假设＋·=，求向量与的夹角．例4 〔1〕设向量、不共线， = 2＋，=＋，=–2，且A、B、D三点共线，求实数的值．〔2〕=2– 3，= 23，其中，不共线，向量=2– 9，问是否存在这样的实数，，使与共线．四、小结1．向量共线的两种处理方法：共线定理和坐标关系；2 向量的两种表现形态：几何表示与坐标表示．要善于转化，向量是处理角的问题重要工具．。

四队中学教案纸 （ 学科： 高一数学 ）备课时间教学 课题2.3.1平面向量的基本定理教时 计划1教学 课时1教学 目标 1．了解平面向量基本定理的概念；2．通过定理用两个不共线向量来表示另一向量或将一个向量分解为两个向量； 3．能运用平面向量基本定理处理简单的几何问题。

重点难点1．平面向量基本定理的应用；2．平面向量基本定理的理解。

教学过程（一）复习引入：（1）向量的加法运算、向量共线定理；（2）设1e r ，2e r 是同一平面内的两个不共线的向量，a r是这一平面内的任一向量，下面我们来研究向量a r 与1e r ，2e r的关系。

（二）新课讲解： 1．平面向量基本定理：如果1e r ，2e r 是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a r，有且只有一对实数1λ，2λ，使1122a e e λλ=+r．其中我们把不共线的向量1e r ，2e r 叫做表示这一平面所有向量的一组基底。

注：①1e r ，2e r均非零向量；②1e r ，2e r不唯一（事先给定）；③1λ，2λ唯一；④20λ=时，a r 与1e r 共线；10λ=时，a r 与2e r 共线；120λλ==时，0a =r r．2．例题分析：例1 已知向量1e r ，2e r （如图），求作向量12235e e -+． 作法：1．如图（2），任取一点O ，作152OA e =-u u u r r，23OB e =u u u r r ；2．作 OACB ，于是OC u u u r是所求作的向量。

例2 如图， 的两条对角线相交于点M ，且AB a =u u u r r ，AD u u u r b =r ，用a r 、b r 表示MA u u u r 、MB u u u r、1e r 2e rMC u u u u r 和MD u u u u r ．解：在中， ABCD ∵AC u u u r AB BC AB AD a b =+=+=+u u u r u u u r u u u r u u u r r r，DB AB AD a b =-=-u u u r u u u r u u u r r r ，∴11()22MA AC a b =-=-+u u u r u u u r r r 1122a b =--r r， 11()22MB DB a b ==-u u u r u u u r r r ，111222MC AC a b ==+u u u u r u u u r r r ， 1122MD MB a b =-=-+u u u u r u u u r r r ．例3 如图，OA u u u r 、OB uuu r 不共线，()AP t AB t R =∈u u u r u u u r，用OA u u u r 、OB uuu r 表示OP uuu r ． 解：∵AP t AB =u u u r u u u r ，∴OP OA AP OA t AB =+=+u u u r u u u r u u u r u u u r u u u r=()(1)OA t OB OA t OA tOB +-=-+u u u r u u u r u u u r u u u r u u u r ．例 4 已知梯形ABCD 中，||2||AB DC =u u u r u u u r ，M ，N 分别是DC 、AB 的中点，若AB u u u r 1e =r，2AD e =u u u r r ，用1e r ，2e r 表示DC u u u r 、BC uuur 、MN u u u u r ． 解：（1）∵DC u u u rAB <∴12DC AB =u u u r u u u r =112e r =12102e e +r r（2）BC AC AB AD DC AB =-=+-u u u r u u u r u u u r u u u r u u u r u u u r 211211122e e e e e =+-=-r r r r r（3）连接DN ，则DN CB =u u u u r u u u r，1()2MN MD DN DC BC =+=-+-u u u u r u u u u r u u u u r u u u r u u u r 1211211112224e e e e e =-⨯-+=-r r r r r ．课外作业1．设G 是ABC ∆的重心.若CA a =u u u r r ，CB b =u u u r r ，试用a r ，b r 表示向量AG u u u r.；2．已知：3AB AM =u u u r u u u u r ，13MN BC =u u u u r u u u r.D b rC B a r A M OBPAAM D CNB。

2012高一数学 2.2.4向量共线定理学案教学目标：1．理解两个向量共线的含义，并能运用它们证明简单的几何问题；2．培养学生在学习向量共线定理的过程中能够相互合作,在不断探求新知识中，培养学生抽象概括能力和逻辑思维能力.教学重点：共线向量定理的应用.教学难点：共线向量定理的应用.教学方法：问题探究式学习.教学过程：一、问题情境问题1 上一节中蚂蚁自西向东3秒钟的位移对应的向量为3a ，记b ＝3a ，b与a 共线吗？a （给出线性表示：如果b λ=a (a ≠0)，则称向量b 可以用非零向量a 线性表示）二、学生活动问题2 对于向量a 和b ，如果有一个实数λ，使得b λ=a ，那么a 与b 共线吗？（可以引导学生从λ的不同取值来探讨（若有向量a 和b ，实数λ，使b λ=a ，则由实数与向量积的定义知：a 与b为共线向量）问题3 如果向量a 和b 共线，是否存在一个实数λ，使b λ=a ？（若a ≠0，a 与b 共线且|b |:|a |μ=，则当a 与b 同向时b μ=a ；当a 与bB D A CE 反向时b =-μa ，从而向量b 与非零向量a 共线的充要条件是：有且只有一个非零实数λ，使b λ=a .）三、构建教学1．整理归纳向量共线定理．如果有一个实数λ，使b λ=a (a ≠0)，那么b 与a 是共线向量；反之，如果b与a (a ≠0)是共线向量，那么有且只有一个实数λ，使b λ= a.2．对定理的理解与证明问题4 为什么要求a 是非零的？b 可以为0吗？若a ＝0，则a , b 总共线，而b ≠0时，则不存在实数λ，使b λ=a 成立；而b= a ＝0时，不管λ取什么值，b λ=a 总成立，λ不唯一.问题5：结合问题2，3的探求，能不能完善定理证明（可以让学生大胆尝试证明，对证明的程序和方法老师要及时给予指导）？四、教学运用1. 例题.例1 如图，E D ,分别为ABC ∆的边AB和AC 中点，求证：→--BC 与→--DE 共线，并将→--DE 用→--BC 线性表示.例2 判断下列各题中的向量是否共线：（1）a =4e 1-25e 2，b =e 1-110e 2； （2）a = e 1＋e 2，b =2 e 1-2 e 2，且1e ，2e 共线．例3 如图2-2-11，ABC ∆中，C 为直线AB 上一点，−→−AC λ=)1(-≠−→−λCB 求证：λλ++=−→−−→−−→−1OB OA OC . 例题提高：上例所证的结论λλ++=−→−−→−−→−1OB OA OC 表明：起点为O ，终点为直线AB 上一点C 的向量−→−OC 可以用,−→−OA −→−OB 表示，那么两个不共线的向量,−→−OA −→−OB 可以表示平面内任一向量吗？2．练习．（1）已知向量a =2e 1-2e 2，b =-3（e 2-e 1），求证：a 与b 是共线向量．（2）已知4MP =u u u r e 12+e 2 ,2PQ =u u u r e 1＋e 2，求证：M ，P ，Q 三点共线．（3）如图，在△ABC 中，12CD AE DA EB ==，记,BC a CA b ==u u u r ， 求证：13DE =u u u r （b －a ）．五、要点归纳与方法小结本节课学习了以下内容:1．两个向量共线的含义；2．两个向量共线（平行）的充要条件；3．能判断两个向量共线.。

向量共线定理教案教学目标：1．理解两个向量共线的含义，并能运用它们证明简单的几何问题；2．培养学生在学习向量共线定理的过程中能够相互合作,在不断探求新知识中，培养学生抽象概括能力和逻辑思维能力教学过程：一、问题情境问题1上一节中蚂蚁自西向东3秒钟的位移对应的向量为3a，记b＝3a，b与a共线吗？aO A二、学生活动问题2 对于向量a和b，如果有一个实数，使得ba，那么a与b共线吗？共线问题3 如果向量a和b共线，是否存在一个实数，使ba？存在的，请学生思考具体是什么？到底有几个？假设b与非零向量a共线，存在λ满足b＝λa；假设b与向量a共线，当a ＝0，b≠0时，不存在λ满足b＝λa三、构建教学1．整理归纳向量共线定理．如果有一个实数λ，使b＝λaa≠0，那么b与a是共线向量；反之，如果b与aa≠0是共线向量，那么有且只有一个实数λ，使b＝λa2．对定理的理解与证明问题4 为什么要求a是非零的？b可以为0吗？a是非零的b可以为0问题5 结合问题2，3的探求，能不能完善定理证明。

学生小组讨论，请学生展示证明过程。

四、题型探究例1 如图，分别为的边和中点，求证：与共线，并将用线性表示例2〔1〕a＝4e1－错误!e2，b＝e1－错误!e2，且e1，e2不共线，求证：a与b共线；〔2〕e1e2e1＋e2，求证：M，P，Q三点共线。

变题：1假设a＝错误!e1－错误!e2，b＝3e1－2e2，判断向量a，b是否共线解∵b＝6a，∴a与b共线〔2〕非零向量e1，e2不共线，如果错误!＝e1＋2e2，错误!＝－5e1＋6e2，错误!＝7e1－2e2，那么共线的三个点是________答案A，B，D解析∵错误!＝e1＋2e2，错误!＝错误!＋错误!＝－5e1＋6e2＋7e1－2e2＝2e1＋2e2＝2错误!∴错误!，错误!共线，且有公共点B，∴A，B，D三点共线反思与感悟1向量共线的判断证明是把两向量用共同的向量来表示，进而互相表示，从而判断共线2利用向量共线定理证明三点共线，一般先任取两点构造向量，从而将问题转化为证明两向量共线，需注意的是，在证明三点共线时，不但要利用b＝λaa≠0，还要说明向量a，b有公共点例3如图2－2－11，中，为直线上一点，，求证：五、稳固练习2、如图，在△ABC中，，记，求证：〔b－a〕．C六、要点归纳与方法小结。