第6章相关与回归分析习题

一、单选题1、下列哪种关系属于相关关系而非函数关系？（）A.销售总额与销售量B.价格与销售量C.工资总额与人均工资D.圆的面积与半径正确答案：B解析： B、函数关系是指现象之间存在的确定性的数量依存关系。

2、若两个变量之间的线性相关系数为0.9，则（）。

A.回归系数为0.81B.判定系数为0.81C.回归估计标准误为0.81D.判定系数为0.95正确答案：B3、下列指标一定非负的是（）。

A.回归系数bB.相关系数rC.回归估计标准误S yxD.回归常数a正确答案：C4、在回归直线方程中y c=a+bx,b 是直线的斜率，表明（）。

A.当x 增加一个单位时,y 增加a的数量B.当y 增加一个单位时,x 的平均增加量C.当y 增加一个单位时,x 增加b的数量D.当x 增加一个单位时,y 的平均增加量正确答案：D5、相关系数r与回归系数b的关系是（）。

A. b=r×S x/S yB. b=r×S y/S xC. r=b×S y/S xD. 以上都不对正确答案：B6、当所有的观察值y都落在直线y c=a+bx上时，x与y之间的相关系数是（）。

A. r=1B.r=-1C. |r|=1D.r=0正确答案：C解析：当r=1或r=-1时，表示变量之间为完全相关7、相关系数r=0表示（）。

A.不存在相关关系B.两变量独立C.不存在线性相关关系D.存在平衡关系正确答案：C8、对相关系数的显著性检验，通常采用的是（）。

A.Z检验B.F检验C.χ2检验D.T检验正确答案：D9、线性回归的检验中，检验整个方程显著性的是（）。

A.F检验B.DW检验C.t检验D.R检验正确答案：A10、下列现象的相关密切程度高的是A.商品销售额与商业利润率之间的相关系数是0.62B.商品销售额与流通费用率之间的相关系数为-0.76C.某商店职工人数与商品销售额之间的相关系数为0.79D.流通费用率与商业利润率之间的相关系数是-0.89正确答案：D二、多选题1、下列属于负相关的现象是（）。

第6章多重共线性的情形及其处理思考与练习参考答案6.1 试举一个产生多重共线性的经济实例。

答：例如有人建立某地区粮食产量回归模型，以粮食产量为因变量Y，化肥用量为X1，水浇地面积为X2，农业投入资金为X3。

由于农业投入资金X3与化肥用量X1，水浇地面积X2有很强的相关性，所以回归方程效果会很差。

再例如根据某行业企业数据资料拟合此行业的生产函数时，资本投入、劳动力投入、资金投入与能源供应都与企业的生产规模有关，往往出现高度相关情况，大企业二者都大，小企业都小。

6.2多重共线性对回归参数的估计有何影响？答：1、完全共线性下参数估计量不存在；2、近似共线性下OLS估计量非有效；3、参数估计量经济含义不合理；4、变量的显著性检验失去意义；5、模型的预测功能失效。

6.3 具有严重多重共线性的回归方程能不能用来做经济预测？答：虽然参数估计值方差的变大容易使区间预测的“区间”变大，使预测失去意义。

但如果利用模型去做经济预测，只要保证自变量的相关类型在未来期中一直保持不变，即使回归模型中包含严重多重共线性的变量，也可以得到较好预测结果；否则会对经济预测产生严重的影响。

6.4多重共线性的产生于样本容量的个数n、自变量的个数p有无关系？答：有关系，增加样本容量不能消除模型中的多重共线性，但能适当消除多重共线性造成的后果。

当自变量的个数p较大时，一般多重共线性容易发生，所以自变量应选择少而精。

6.5 自己找一个经济问题来建立多元线性回归模型，怎样选择变量和构造设计矩阵X才可能避免多重共线性的出现？答：请参考第三次上机实验题——机场吞吐量的多元线性回归模型，注意利用二手数据很难避免多重共线性的出现，所以一般利用逐步回归和主成分回归消除多重共线性。

如果进行自己进行试验设计如正交试验设计，并收集数据，选择向量使设计矩阵X 的列向量（即X 1，X 2， X p ）不相关。

6.6对第5章习题9财政收入的数据分析多重共线性，并根据多重共线性剔除变量。

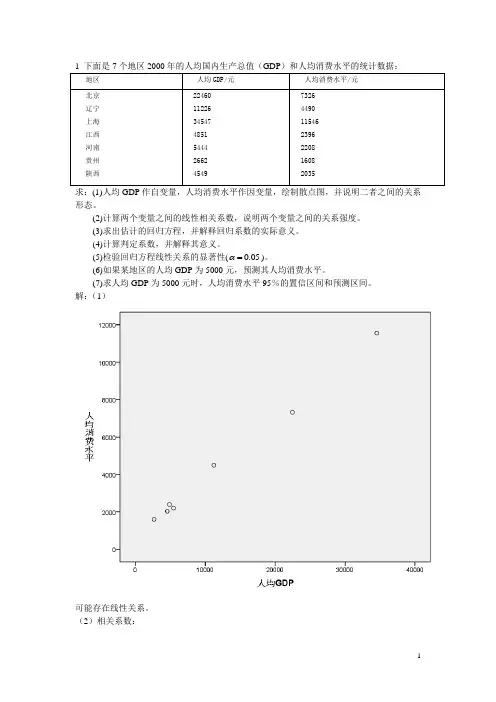
1 下面是7个地区2000年的人均国内生产总值（GDP）和人均消费水平的统计数据：地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求：(1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。

(2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。

(3)求出估计的回归方程，并解释回归系数的实际意义。

(4)计算判定系数，并解释其意义。

(5)检验回归方程线性关系的显著性(0.05α=)。

(6)如果某地区的人均GDP为5000元，预测其人均消费水平。

(7)求人均GDP为5000元时，人均消费水平95％的置信区间和预测区间。

解：（1）可能存在线性关系。

（2）相关系数：（3）回归方程：734.6930.309y x=+回归系数的含义：人均GDP没增加1元，人均消费增加0.309元。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 （常量）734.693 139.540 5.265 0.003人均GDP（元）0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平（元）%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（4）模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。

人均GDP对人均消费的影响达到99.6%。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

第六章 相关与回归分析方式第一部份 习题一、单项选择题1.单位产品本钱与其产量的相关；单位产品本钱与单位产品原材料消耗量的相关 ( )。

A.前者是正相关，后者是负相关 B.前者是负相关，后者是正相关2.样本相关系数r 的取值范围( )。

∞＜r ＜+∞≤r ≤1 C. -l ＜r ＜1 D. 0≤r ≤101y x ββ=+上，那么x 与y 之间的相关系数( )。

A.r ＝0B.r ＝1C.r ＝-1D.|r|＝14.相关分析与回归分析，在是不是需要确信自变量和因变量的问题上( )。

A.前者无需确信，后者需要确信 B.前者需要确信，后者无需确信5.直线相关系数的绝对值接近1时，说明两变量相关关系的紧密程度是( )。

6.年劳动生产率x(千元)和工人工资y(元)之间的回归方程为y=10+70x ，这意味着年劳动生产率每提高1千元时，工人工资平均( )。

7.下面的几个式子中，错误的选项是( )。

8.以下关系中，属于正相关关系的有( )。

9.直线相关分析与直线回归分析的联系表现为( )。

10.进行相关分析，要求相关的两个变量( )。

A.都是随机的B.都不是随机的11.相关关系的要紧特点是( )。

B.某一现象的标志与另外的标志之间存在着必然的关系，但它们不是确信的关系12.相关分析是研究( )。

13.现象之间彼此依存关系的程度越低，那么相关系数( )。

01y x ββ=+中，假设10β<，那么x 与y 之间的相关系数( )。

A. r=0B. r=1C. 0＜r ＜1D. —l ＜r ＜0 15.当相关系数r=0时，说明( )。

A.现象之间完全无关B.相关程度较小16.已知x 与y 两变量间存在线性相关关系，且210,8,7,100xy xy n σσσ===-=，那么x 与y 之间存在着( )。

17.计算估量标准误差的依据是( )。

A.因变量的数列B.因变量的总变差18.两个变量间的相关关系称为( )。

回归分析练习题（有答案）作者:日期:1.1回归分析的基本思想及其初步应用一、选择题1.某同学由x 与y 之间的一组数据求得两个变量间的线性回归方程为均值为2，数据y 的平均值为3，则（）A .回归直线必过点（2,3）C 点（2,3）在回归直线上方B.回归直线一定不过点（2,3）D 点（2,3）在回归直线下方y bx a ，已知：数据x 的平2.在一次试验中，测得（x, y）的四组值分别是A （1,2）,B（2,3）,C（3,4）,D（4,5），则丫与X 之间的回归直线方程为（）A.$x1B .$ x 2C$2x1D.$ x 13.在对两个变量x ，y 进行线性回归分析时，有下列步骤：①对所求出的回归直线方程作出解释；③求线性回归方程；④求未知参数；②收集数据（X j 、y i ），i 1,2，…，n ；⑤根据所搜集的数据绘制散点图）如果根据可行性要求能够作岀变量A.①②⑤③④Bx, y 具有线性相关结论，则在下列操作中正确的是（C.②④③①⑤D .②⑤④③①.③②④⑤①4.下列说法中正确的是（）B人的知识与其年龄具有相关关系D 根据散点图求得的回归直线方程都是有意义的A.任何两个变量都具有相关关系C.散点图中的各点是分散的没有规律5.给出下列结论：2 2（1）在回归分析中，可用指数系数R 的值判断模型的拟合效果，R 越大，模型的拟合效果越好；（2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；（3）在回归分析中，可用相关系数r 的值判断模型的拟合效果，较合适带状区域的宽度越窄，说明模型的拟合精度越高.A.y 平均增加1.5个单位B.A. 1B )个..2r 越小，模型的拟合效果越好；（4）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比y 平均增加2个单位C.y 平均减少1.5个单位C.3DD.y 平均减少2个单位.4以上结论中，正确的有（6.已知直线回归方程为y7.2 1.5x ，则变量x 增加一个单位时（)下面的各图中，散点图与相关系数r 不符合的是（）\ 1V ||一1,— 1 < r<(>■r?■* ■■■■* ■..* .**打4X（7UV1）D.'8.一位母亲记录了儿子39岁的身高，由此建立的身高与年龄的回归直线方程为据此可以预测这个孩子10岁时的身高，则正确的叙述是（A.身高一定是145.83cm C.身高低于145.00cm BD）7.19x 73.93,.身高超过146.00cm身高在145.83cm左右9.（A）预报变量在x轴上，解释变量在y轴上（B）解释变量在x轴上，预报变量在y轴上（C）（D）在画两个变量的散点图时，下面哪个叙述是正确的（）可以选择两个变量中任意一个变量在x轴上可以选择两个变量中任意一个变量在y轴上10.两个变量y与x的回归模型中，通常用R2来刻画回归的效果，则正确的叙述是（22）A.R越小，残差平方和小2B.R越大，残差平方和大2c.R于残差平方和无关D.R越小，残差平方和大211.两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟合效果最好的模型是（）A.模型1的相关指数R2为0.98 B.模型2的相关指数R2为0.802 2C.模型3的相关指数R为0.50 D.模型4的相关指数R为0.2512.回归直线上相应位置的差异的是A.总偏差平方和B.C.回归平方和13.回归直线方程为残差平方和D.相关指数R2在回归分析中，代表了数据点和它在（）工人月工资（元）依劳动生产率（千元）变化的60 90x，下列判断正确的是（）A.劳动生产率为1000元时，工资为50元B.劳动生产率提高1000元时，工资提高150元C.劳动生产率提高1000元时，工资提高90元D.劳动生产率为1000元时，工资为90元14.下列结论正确的是（）①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.A.①② E.①②③ C.①②④ D.①②③④15.已知回归直线的斜率的估计值为中心为（4,5），则回归直线方程为（）1.23，样本点的A.$ 1.23x 4B.$ 1.23x 5C.$ 1.23x 0.08D.y 0.08x 1.2316.在比较两个模型的拟合效果时，甲、乙两个模型的相关指数果好的模型是 __________.17.在回归分析中残差的计算公式为 ____________.18.线性回归模型y bx a e（a和b为模型的未知参数）中，e称为_________________.19.若一组观测值（X1,yJ（X2,y2）…（Xn,y“）之间满足yi=bXi+a+e（i=1、2.…n）若恒为0,则氏为______________R2的值分别约为0.96和0.85，则拟合效20.调查某市出租车使用年限x 和该年支出维修费用y (万元)，得到数据如下:使用年限x 维修费用y(求线性回归方程;n22.233.845.556. 567.0(2)由(1)中结论预测第10年所支出的维修费用.i 1(X i x) (y iy).n(X ii 1x)2bx21.以下是某地搜集到的新房屋的销售价格闵屋面积Ey 和房屋的面积x 的数据:11524.Q1102 1. CIB-413G29.21口丘22t 肖年愉梧(1)画岀数据对应的散点图；(2)求线性回归方程，并在散点图中加上回归直线；(3)据(2)的结果估计当房屋面积为150m2时的销售价格(4)求第2个点的残差。

第六章 相关与回归分析思考与练习一、判断题1.产品的单位成本随着产量增加而下降，这种现象属于函数关系。

答：错。

应是相关关系。

单位成本与产量间不存在确定的数值对应关系。

2.相关系数为0表明两个变量之间不存在任何关系。

答：.错。

相关系数为零，只表明两个变量之间不存在线性关系，并不意味着两者间不存在其他类型的关系。

3.单纯依靠相关与回归分析，无法判断事物之间存在的因果关系。

答：对，因果关系的判断还有赖于实质性科学的理论分析。

4.圆的直径越大，其周长也越大，两者之间的关系属于正相关关系。

答：错。

两者是精确的函数关系。

5.总体回归函数中的回归系数是常数，样本回归函数中的回归系数的估计量是随机变量。

答：对。

6.当抽取的样本不同时，对同一总体回归模型估计的结果也有所不同。

答：对。

因为，估计量属于随机变量，抽取的样本不同，具体的观察值也不同，尽管使用的公式相同，估计的结果仍然不一样。

二、选择题1.变量之间的关系按相关程度分可分为：b 、c 、da.正相关；b. 不相关；c. 完全相关；d.不完全相关； 2.复相关系数的取值区间为：aa. 10≤≤R ；b.11≤≤-R ；c.1≤≤∞-R ；d.∞≤≤-R 1 3.修正自由度的决定系数a 、b 、da.22R R ≤； b.有时小于0 ； c. 102≤≤R ；d.比2R 更适合作为衡量回归方程拟合程度的指标 4.回归预测误差的大小与下列因素有关：a 、b 、c 、da 样本容量；b 自变量预测值与自变量样本平均数的离差c 自变量预测误差；d 随机误差项的方差三、问答题1．请举一实例说明什么是单相关和偏相关？以及它们之间的差别。

答：例如夏季冷饮店冰激凌与汽水的消费量，简单地就两者之间的相关关系进行考察，就是一种单相关，考察的结果很可能存在正相关关系，即冰激凌消费越多，汽水消费也越多。

然而，如果我们仔细观察，可以发现一般来说，消费者会在两者中选择一种消费，也就是两者之间事实上应该是负相关。

练习题6（相关系数与回归分析）1某电视台非常关心新闻节目的受欢迎程度；电视节目的受欢迎程度由一套评估体系来决定，这个评估体系对每个被评估的节目评级：由1（最低）到10（最高）。

某电视台认为在新闻节目之前的节目的受欢迎程度会影响到新闻节目的受欢迎程度。

为此，他们搜集了一组30个样本，其中包含两个变量：x-新闻节目之前的节目评级；y-新闻节目的评级，数据列于为研究x与y二者之间的关系，计算相关系数，并对其进行检验。

3 使用四川绵阳地区3年生中山柏的数据“中山柏.sav”，分析月生长量与平均气温、月降雨量、月平均日照时数、月平均湿度这4个气候因素哪个因素有关？回归分析：4 零售商要了解每周的广告费X及消费额Y之间关系，记录如下数据：画出散点图，并在Y对X回归为线性的假定下，用最小二乘法算出一元回归方程.5 某厂生产某产品，其成本费用（Y，万元）与劳动量（X1，千小时）及原材料价格（X 2，万元／万吨）有密切关系。

下面列出了2002年1月～2003年6月的成本、劳动量、原材料价格资料。

要求：（1）建立二元线性回归方程，对回归系数b1、b2进行合理的解释。

（2）对所建立的回归方程进行显著性检验；（3）假定2003年7月份劳动量X1=1.19千小时，X2=2.31万元／万吨，试预测2003年7月份的成本费用。

6 用第2题资料，计算身高与坐高、体重、胸围、肩宽和骨盆宽等变量的Pearson相关关系，并用逐步回归建立方程。

(引入原则P<0.05,剔除原则P>0.051)7用第1题资料，假定模型为：y=β0+β1Xi+εi i= 1，…，30用最小二乘法估计模型参数，建立线性回归模型，对回归系数进行显著性检验，对β1的置信水平作95%的区间估计。

对x=8时的y值作预测，并作95%的预测区间。

8 家庭信用卡消费多寡与家庭年收入及家庭人口有关，具体数据如下表，要求：①做消费金额与家庭人口，消费金额与年收入的散点图；②因变量、自变量分别是什么；③建立回归方程，讨论这三者之间的关系；④讨论哪个因素对因变量影响大，理由是什么？被调查对象的家庭年收入（万元）、家庭人口和信用卡消费的金额（元）。