答案 拓扑学基础A

基础拓扑学讲义1. 引言拓扑学是数学的一个分支，研究的是空间中的集合如何存在和连接的学科。

在拓扑学中，我们关注的是集合之间的关系，而不是集合的具体性质。

本讲义将介绍拓扑学的基础知识和常见概念。

2. 基本概念2.1 集合在拓扑学中，一个集合是指由元素组成的无序对象的集合。

示例：- 集合 A = {1, 2, 3, 4}- 集合 B = {a, b, c}2.2 拓扑空间拓扑空间是指一个集合论中的空间，其中具有一组满足特定条件的子集。

示例：- 欧几里得空间- 流形空间- 度量空间2.3 拓扑结构拓扑结构是指在拓扑空间中定义的一组特殊集合的集合，它满足特定的公理。

示例：- 开集- 闭集- 连通集- 紧集3. 拓扑学的基本性质3.1 连通性在拓扑学中，连通性是指一个拓扑空间中不存在将空间分为两个或更多部分的拓扑属性。

示例：- 实数集 R 是一个连通集- 平面上的一个圆形是一个连通集3.2 完备性在拓扑学中，完备性是指拓扑空间中的每个柯西序列都有一个收敛的极限。

示例：- 实数集 R 是一个完备的度量空间3.3 紧集在拓扑学中，一个集合被称为紧集，如果它的每个开覆盖都具有有限子覆盖。

示例：- 闭区间 [0, 1] 是一个紧集4. 拓扑学的应用拓扑学在各个领域都有广泛的应用，包括物理学、生物学、计算机科学等。

示例：- 电路板设计中的连接问题- 生物分子的空间构象研究- 网络拓扑结构的分析与优化5. 总结本讲义介绍了拓扑学的基本概念、拓扑结构和其应用。

拓扑学作为一门重要的数学学科，对于理解和描述空间的性质具有重要的作用。

希望通过本讲义的学习，能够对拓扑学有一个初步了解，并能够应用于实际问题中。

注意：本讲义只是拓扑学的入门讲义，如果想深入学习拓扑学，请参考相关的高级教材和论文。

马克阿姆斯特朗基础拓扑学答案马克阿姆斯特朗()是美国著名的物理学家、发明家。

他于1946年在哥伦比亚大学获得物理学博士学位,1953年开始在耶鲁大学教授物理学,1969年开始在美国斯坦福大学任教。

1971年至1977年担任美国国家科学院院士。

1985年获得美国艺术与科学院外籍院士。

他还是美国物理学会、国际数学会议和()等学术组织的成员。

一、拓扑学研究的主要内容是什么？拓扑学是研究一类不定的几何图形和空间形式之间的相互关系的一门学科。

它的基本思想是：对给定的几何图形或空间形式，可求出任意几何图形或空间形式上所对应着的有限个数。

拓扑学包括两个部分：一为线性拓扑学；二为几何拓扑学。

线性拓扑学指对于给定几何图形或空间形式在有限个数范围内，可求出任意几何图形或空间形式上所对应着的有限个数；几何拓扑学则是将不定几何图形、空间形式上所对应着的有限个数推广到有限个数范围内，并求得该有限个数对应着某个区间或领域内某一具体对象或事物中之最小个数或最大个数点所对应着的有限个数。

拓扑学通过对给定几何图形或空间形式上所对应着有限个数或最大个位数个点所对应着相应事物中之最小个数或最大个位数点所对应着有限个数或最大个位数点所对应着之最大个数点对应着相应事物中之最小个数点所在区域或领域所对应着之最小点所对应着的总个数（包括其个数大小和方向）来解决有限个数或最大个位数、局部个数和领域个数之间的关系。

拓扑学中一些特殊几何图形和空间形式所对应着一系列数学问题都属于拓扑学理论中所涉及到之问题。

二、对一条长波在时空中运动是什么性质？解析：由于运动波是波传播过程中产生的一种特殊的传播现象，因此，对于一条运动波波速必须满足如下条件：波穿过空间（或时间）必须有一个连续的运动状态，在该运动状态中，波向一个特定地方或一个方向（或几个方向）运动而不能出现位移叠加等现象。

否则该波将被视作一个静止波，其能量为0。

此外，运动波是一种波速传播过程中产生或传播方向相反的运动状态，因此传播波波速必须满足以下条件：一是运动波向该运动状态所处方向相切才能实现对波与波之间相互作用作用（波速与振幅方向）所产生频率变化速率相一致；二是波速与运动方向相切才能实现对波与波之间相互作用作用（波速与振幅方向相一致）所产生频率变化速率相一致。

考研拓扑学试题及答案一、选择题（每题3分，共30分）1. 在拓扑学中，一个集合的子集被称为开集，如果它是全空间的开集。

以下哪个选项不是开集的特征？A. 包含空集B. 任意两个开集的交集是开集C. 任意有限个开集的并集是开集D. 任意无限个开集的并集不是开集2. 拓扑空间中的一个基本性质是连续性。

以下哪个选项不是连续函数的特征？A. 函数的逆像是开集B. 函数的值域是开集C. 函数的图像是连续的曲线D. 函数在其定义域内连续3. 以下哪个命题是正确的？A. 有限个连通空间的不交并仍然是连通的B. 任意个连通空间的不交并是连通的C. 任意个连通空间的并集是连通的D. 有限个连通空间的并集是连通的4. 在拓扑空间中，一个点的闭包是指包含该点的最小闭集。

以下哪个说法是错误的？A. 闭包是闭集B. 闭包包含该点的所有邻域C. 闭包是唯一的D. 闭包可能是开集5. 以下哪个选项不是紧空间的特征？A. 任意开覆盖都有有限子覆盖B. 任意序列都有收敛的子序列C. 任意闭区间是紧的D. 任意闭集在空间中是紧的6. 拓扑空间中的分离公理是描述空间中点和子集之间关系的一种性质。

以下哪个选项是错误的？A. T0空间中，每个点由其闭包唯一确定B. T1空间中，每个点由其开核唯一确定C. T2空间中，任意两个不同点都由不相交的开集分离D. T3空间中，任意闭集和任意开集都由不相交的开集分离7. 以下哪个命题是错误的？A. 任意两个拓扑空间的乘积空间是豪斯多夫空间B. 任意两个豪斯多夫空间的乘积空间是豪斯多夫空间C. 任意两个紧致空间的乘积空间是紧致的D. 任意两个可数紧空间的乘积空间是可数紧的8. 以下哪个选项不是局部紧空间的特征？A. 每个点都有一个紧致的邻域B. 空间本身是紧致的C. 每个点都有一个开集邻域，其闭包是紧致的D. 每个点都有一个紧致子集作为其邻域9. 以下哪个命题是正确的？A. 任意两个拓扑空间的和空间是豪斯多夫空间B. 任意两个豪斯多夫空间的和空间是豪斯多夫空间C. 任意两个紧致空间的和空间是紧致的D. 任意两个可数紧空间的和空间是可数紧的10. 在拓扑空间中，一个点的导集是指所有包含该点的序列的极限点的集合。

1.在拓扑空间中，下列哪项不是开集的定义？o A. 开集是拓扑空间中的一个集合，它属于该空间的拓扑。

o B. 开集是所有点的邻域。

o C. 开集是所有点的闭包。

o D. 开集是包含在它自身的邻域内的集合。

参考答案: C. 开集是所有点的闭包。

解析: 开集的定义是它属于拓扑空间的拓扑，即它是一个邻域，包含在它自身的邻域内，但开集不是所有点的闭包，闭包是开集的补集的补集。

2.下列哪项不是拓扑空间的定义？o A. 一个集合和它的子集族，其中包含空集和全集。

o B. 任意多个开集的并集仍然是开集。

o C. 有限多个开集的交集仍然是开集。

o D. 任意多个闭集的并集仍然是闭集。

参考答案: D. 任意多个闭集的并集仍然是闭集。

解析: 拓扑空间的定义包括集合和它的子集族，其中包含空集和全集，任意多个开集的并集和有限多个开集的交集仍然是开集，但任意多个闭集的并集不一定是闭集。

3.在拓扑学中，下列哪项不是连续函数的定义？o A. 对于函数f的定义域中的任意开集，其像集也是开集。

o B. 对于函数f的值域中的任意开集，其原像集也是开集。

o C. 函数f在其定义域的每一点都是连续的。

o D. 函数f在其值域的每一点都是连续的。

参考答案: A. 对于函数f的定义域中的任意开集，其像集也是开集。

解析: 连续函数的定义是对于函数f的值域中的任意开集，其原像集也是开集，函数在其定义域的每一点都是连续的，但函数f的定义域中的开集的像集不一定是开集。

4.下列哪项不是紧致空间的定义？o A. 紧致空间中的任意开覆盖都有有限子覆盖。

o B. 紧致空间中的所有序列都有收敛子序列。

o C. 紧致空间中的所有连续函数都有界。

o D. 紧致空间中的所有连续函数都有最大值和最小值。

参考答案: B. 紧致空间中的所有序列都有收敛子序列。

解析: 紧致空间的定义是任意开覆盖都有有限子覆盖，所有连续函数都有界和最大最小值，但紧致空间中的所有序列不一定都有收敛子序列。

《拓扑学》题库及答案一、单项选择1．关于笛卡儿积，下面等式成立的是（A ）)()()()(D B C A D C B A ⨯-⨯=-⨯- （B ）)()()()(D C B A D B C A I I I ⨯=⨯⨯ （C ）)()()()(D B C A D C B A ⨯⨯=⨯Y Y Y （D ）D B C A ⨯⊆⨯当且仅当D C B A ⊆⊆,2．设Y X f →:是映射，)(,,X B A P ∈，)(,Y D C P ∈，则下面结论不成立的是： （A ）)()()(111D f C f D C f ---=Y Y （B ）)()()(111D f C f D C f---=I I（C ）)()()(B f A f B A f Y Y = （D ）)()()(B f A f B A f I I =3．在字典序拓扑空间++⨯Z Z 中，子集+⨯Z }2{是：（A ）开集，非闭集 （B ）闭集，非开集 （C ）即开，且闭集 （D ）即非开集，也非闭集4．设R R →2:d 为映射，（R 表示实数集合），R ∈∀y x ,，下面关于d 的定义中是R 的度量的是：（A ）2(,)()d x y x y '=- （B ）22),(y x y x d -=（C ）||||),(y x y x d += （D ）⎩⎨⎧=≠=yx yx y x d 01),(5．设)T ,(X 是平庸拓扑空间，b a X b a ≠∈,,，则交错序列Λb a b a ,,,在拓扑空间)T ,(X 中的收敛点集合是： （A ）∅ （B ）}{a （C ）},{b a （D ）X6．设}},{},{,,{},3,2,1{},,,{1b a a X Y c b a X ∅===T ，}}2{},3,2{},2,1{,,{2Y ∅=T ，}{b A =，}1{=B ，则在积空间Y X ⨯中B A ⨯等于（A ）)}1,{(b （B ）)}1,(),1,{(c b（C ）)}2,(),1,{(b b （D ）)}2,(),1,(),2,(),1,{(c c b b7．设},,,{d c b a X =，{,,{,,},{,,},{,}}x a b c b c d b c =∅T ，},,{d c a Y =，},{c a A =，则在子空间Y 中A 的内部等于：（A ）∅ （B ）}{a （C ）}{c （D ）},{c a8．拓扑空间的Lindel öff 性，可分性，紧致性，完全正则性中是有限可积性质的有： （A ）1个 （B ）2个 （C ）3个 （D ）4个 9．下列拓扑空间的蕴涵关系中，成立的有完全正则空间⇒正则空间，完全正则空间⇒正规空间，连通空间⇒局部连通空间， 度量空间⇒可分空间，度量空间⇒Lindel öff 空间（A ）1个 （B ）2个 （C ）3个 （D ）4个10．拓扑空间的可分性，紧致性，Lindel öff 性，连通性中在连续射下保持不变的性质有： （A ）1个 （B ）2个 （C ）3个 （D ）4个 11．设X X R ⨯⊆是一个等价关系，则R 不满足的条件是（A ）R X ⊆∆)( （B ）R ∩R -1=∅ （C ）R R R ⊆ο （D ）1-=R R12．设Y X f →:是映射，)(}|{X J A P ⊆∈αα，)(}|{Y r B r P ⊆Γ∈则下面等式中不成立的是 （A ）)()(ααααA f A f JJ∈∈=Y Y （B ）)()(ααααA f A f JJ∈∈=II（C ）)()(11r r r r B f B f-Γ∈Γ∈-=Y Y （D ）)()(11r r r r B f B f -Γ∈Γ∈-I I13．在字典序拓扑空间++⨯Z Z 中，子集+⨯Z }1{是：（A ）开集，非闭集 （B ）闭集，非开集 （C ）即开，且闭集 （D ）即非开集，亦非闭集14．设},,{c b a X =，}},{},{,,{b a a X ∅=T ，则在拓扑空间)T ,(X 中常值序列Λ,,a a 的 收敛点集合是 （A ）}{a （B ）},{c a （C ）},{b a （D ） X15．设},,{c b a X =，}3,2,1{=Y ，}{},{},{,,{c b a X ∅=1T ，}}3,2{},2{},2,1{,,{Y ∅=2T ，}2,1{},,{==B b a A ，则在积空间Y X ⨯中，0)(B A ⨯等于：（A ）∅ （B ）}{)2,(),1,(a a （C ）}{)2,(),1,(b b （D ）}{)2,(),1,(),2,(),1,(b b a a16.设},,,{d c b a X =，}},{},,,{},,,{,,{d c d c a d c b X ∅=T ，}{},,,{c A d c a Y ==，则在子空间Y 中，A 的闭包等于（A ）}{c （B ）},{a c （C ）},{b c （D ）},,{c d a17．设)T ,(X 是拓扑空间，)T ,(X 是可度量空间是指存在X 的度量R →2:X d 使得由d 诱导的拓扑d T 满足： (A)T T ⊆d (B)d T T ⊆ (C)d T T = (D))(X P T d = 18．拓扑空间的可分性，Lindel öff 性, 正规性、完全正则性中是遗传性质的有 （A ）1个 (B) 2个 (C) 3个 (D) 4个 19．下列拓扑空间的蕴涵关系中成立的有满足第二可数理空间⇒可分空间 度量空间⇒Lindel öff 空间 正规空间⇒完全正则空间 度量空间⇒满足第一可数公理空间 正规空间⇒正则空间 完全正则空间⇒正则空间 （A ）1个 （B ）2个 （C ）3个 （D ）4个20．设),(T X 是拓扑空间，则对X 中任意两个不相交闭集B A ,存在连续映射]1,0[:→X f 使得}0{)(⊆A f ，}1{)(⊆B f 当且仅当),(T X 是：（A ）正则空间 （B ）完全正则空间 （C ）正规空间 （D ）4T 空间 21．设X 是全集，,()A B X ∈P ，A B ⊆则当且仅当（A ）∅='B A I （B ）∅='B A I （C ）A B A =Y （D ）B B A =I 22．设Y X f →:是映射，,()A B y ∈P ，则下面结论不成立的是（A ）)()()(111B f A f B A f ---=Y Y （B ）111()()()f A B f A f B ---=I I （C ）)()()(111B f A fB A f----=- （D ）()B B f f =-)(123．在字典序拓扑空间+⨯Z }2,1{中，子集+⨯Z }2{是（A ）开集，非闭集 （B ）闭集，非开集 （C ）即开，且闭集 （D ）即非开集，亦非闭集 24．定义度量R R R →⨯22:d ，),(21x x x =∀，221),(R ∈=y y y ，}{|||,|m ax ),(2211y x y x y x d --=，则度量空间（d ,2R ）中的单位球是（A （B ）（C （D ）25．设)T ,(X 是离散拓扑空间，b a X b a ≠∈,,, 则在)T ,(X 中交错序列Λb a b a ,,,的收敛点集合是 （A ）∅ (B) }{a (C) },{b a (D)X26．设},,,,{d c b a X =}},{},,,{},,,{,,{c b d c b c b a X T ∅=，},,{c b a Y =，}{b A =，则在子空间Y 中A 的闭包等于（A ）}{b （B ）},{b a （C ）},{c b （D ）},,{c b a27．设}3,2,1{},,,{==Y c b a X ，}{,,{,},{},{,}X a b b b c =∅1T ，}{}2,1{},1{,,2Y ∅=T ，},{c b A =，}3,1{=B 则在积空间Y X ⨯中()o A B ⨯等于（A ）∅ （B ）}{)2,(),1,(b b （C ）}{)1,(),1,(c b （D ）}{(,1),(,2),(,1),(,2)b b c c28．拓扑空间的连通性、紧致性、可分性、完全正则性，Lindel öff 性，满足第二可数公理性中是可遗传性质的有（A ）1个 （B ）2个 （C ）3个 （D ）4个 29．下列拓扑空间之间的蕴涵关系中成立的有：满足第二可数合理空间⇒可分空间， 度量空间⇒满足第一可数公理空间 完全正则空间⇒正则空间， 紧致空间⇒Lindel öff 空间 （A ）1个 （B ）2个 （C ）3个 （D ）4个}0{)(⊆A f ，}1{)(⊆B f 当且仅当),(T X 是：（A ）正则空间 （B ）完全正则空间 （C ）正规空间 （D ）4T 空间 31．设f Y X f ,⨯⊆是映射，则f 满足的条件是 （A ）X Y f =-)(1；如果f y x y x ∈),(),,(21，则21y y =（B ）X Y f=-)(1；如果f y x y x ∈),(),,(21，则21x x =（C ）Y X f =)(；如果f y x y x ∈),(),,(21，则21y y = （D ）Y X f =)(；如果f y x y x ∈),(),,(21，则21x x =32．设,,(),,(),R X Y A B Y C D X ⊆⨯∈∈P P 则下面等式成立的是 （A ）)()()(111B R A R B A R---=Y Y （B ）)()()(111B R A R B A R ---=I I（C ）)()()(D R C R D C R I I = （D ）)()()(D R C R D C R -=- 33．在字典序拓扑空间+⨯Z }2,1{中，子集+⨯Z }2{是（A ）开集，非闭集 （B ）闭集，非开集 （C ）即开，且闭集 （D ）即非开集，亦非闭集 34．设),(d X 是度量空间，d T 是X 的由d 诱导的拓扑，dU ∈T ，则下列关于U 的结论不正确的是（A ）存在0,>∈εX x 使得),(εx B U =（B ）+∈∃∈∀Z n U x ,使得U nx B ⊆)1,(（C ）0,>∃∈∀εU x 使得U x B ⊆),(ε（D ）存在}0,|),({>∈⊆εεX x x B U B 使得U U =U B35．设},,,{c b a X =}{},{},{,,{b a a X ∅=T ，则在拓扑空间),(T X 中常值序列,,,a a a …的收敛点集合是 （A ）}{a （B ）},{c a （C ）},{b a （D ）X36．设},,,{c b a X =}},{},,,{},,,{,,{c b d c b c b a X ∅=T ，},,,{d c a Y =},{c a A =，则在子空间Y 中A 的内部是（A ）∅ （B ）}{a （C ）}{c （D ）},{c a37．设},,,{c b a X =},3,2,1{=Y }},{},{,,{b a a X ∅=1T ，}}3,2{},2{},2,1{,,{2Y ∅=T ，}1{},{==B b A ，则在积空间Y X ⨯中，B A ⨯等于（A ）)}1,{(b （B ）)}1,(),1,{(c b（C ）)}2,(),1,{(b b （D ）)}2,(),1,(),2,(),1,{(c c b b38．拓扑空间的可分性，Lindel öff 性，紧致性，正规性，连通性中是有限可积的性质有： （A ）1个 （B ）2个 （C ）3个 （D ）4个 39．下列拓扑空间之间的蕴涵关系中成立的有正规空间⇒正则空间 完全正则空间⇒正则空间 局部连通空间⇒连通空间 满足第二可数公理空间⇒可分空间 度量空间⇒满足第一可数公理空间 度量空间⇒可分空间}1{)(,0)(⊆=A f x f 当且仅当),(T X 是（A ）1T 空间 （B ）正规空间 （C ）完全正则空间 （D ）4T 空间二．证明题1.设Y X ,是两个拓扑空间，Y X f →:是映射，证明若f 是连续映射，则)(Y B Ρ∈∀，11()(())o o fB f B --⊆。

点集拓扑学练习题一、单项选择题（每题2分）1、已知{,,,,}X a b c d e =,下列集族中，（ ）是X 上的拓扑.① {,,{},{,},{,,}}X a a b a c e φ=T② {,,{,,},{,,},{,,,}}X a b c a b d a b c e φ=T③ {,,{},{,}}X a a b φ=T④ {,,{},{},{},{},{}}X a b c d e φ=T2、设{,,}X a b c =，下列集族中,（ ）是X 上的拓扑.① {,,{},{,},{}}X a a b c φ=T ② {,,{},{,},{,}}X a a b a c φ=T③ {,,{},{},{,}}X a b a c φ=T ④ {,,{},{},{}}X a b c φ=T3、已知{,,,}X a b c d =,下列集族中，（ ）是X 上的拓扑.① {,,{},{,},{,,}}X a a b a c d φ=T ② {,,{,,},{,,}}X a b c a b d φ=T ③ {,,{},{},{,,}}X a b a c d φ=T ④ {,,{},{}}X a b φ=T4、设{,,}X a b c =，下列集族中,（ ）是X 上的拓扑.① {,,{},{},{,}}X b c a b φ=T ② {,,{},{},{,},{,}}X a b a b a c φ=T ③ {,,{},{},{,}}X a b a c φ=T ④ {,,{},{},{}}X a b c φ=T5、已知{,,,}X a b c d =,下列集族中，（ ）是X 上的拓扑.① {,,{,},{,,}}X a b a c d φ=T ② {,,{,},{,,}}X a b a c d φ=T③ {,,{},{},{,,}}X a b a c d φ=T ④ {,,{},{},{,}}X a c a c φ=T6、设{,,}X a b c =，下列集族中,（ ）是X 上的拓扑.① {,,{},{},{,}}X a b b c φ=T ② {,,{,},{,}}X a b b c φ=T③ {,,{},{,}}X a a c φ=T ④ {,,{},{},{}}X a b c φ=T7、已知{,,,}X a b c d =，拓扑{,,{}}X a φ=T ,则}{b =（ ）①φ ② X ③ {}b ④ {,,}b c d8、 已知{,,,}X a b c d =，拓扑{,,{}}X a φ=T ,则{,,}b c d =（ ）①φ ② X ③ {}b ④ {,,}b c d9、 已知{,}X a b =，拓扑{,,{}}X a φ=T ,则{}a =（ ）①φ ② X ③ {}a ④ {}b10、已知{,}X a b =，拓扑{,,{}}X a φ=T ,则{}b =（ ）①φ ② X ③ {}a ④ {}b11、已知{,,,}X a b c d =，拓扑{,,{}}X a φ=T ,则{}a =（ ）①φ ② X ③ {,}a b ④ {,,}b c d12、已知{,,,}X a b c d =，拓扑{,,{}}X a φ=T ,则{}c =（ ）①φ ② X ③ {,}a c ④ {,,}b c d13、设{,,,}X a b c d =，拓扑{,,{},{,,}}X a b c d φ=T ,则X 的既开又闭的非空真子集的个数为（ ） ① 1 ② 2 ③ 3 ④ 414、设{,,}X a b c =，拓扑{,,{},{,}}X a b c φ=T ,则X 的既开又闭的非空真子集的个数为（ ）① 1 ② 2 ③ 3 ④ 415、设{,,}X a b c =，拓扑{,,{},{,}}X b b c φ=T ,则X 的既开又闭的非空真子集的个数为（ ）① 0 ② 1 ③ 2 ④ 316、设{,}X a b =，拓扑{,,{}}X b φ=T ,则X 的既开又闭的子集的个数为（ ）① 0 ② 1 ③ 2 ④ 317、设{,}X a b =，拓扑{,,{},{}}X a b φ=T ,则X 的既开又闭的子集的个数为（ ）① 1 ② 2 ③ 3 ④ 418、设{,,}X a b c =，拓扑{,,{},{},{,},{,}}X a b a b b c φ=T ,则X 的既开又闭的非空真子集的个数为（ ）① 1 ② 2 ③ 3 ④ 419、在实数空间中，有理数集Q 的内部Q 是（ ）① φ ② Q ③ R -Q ④ R20、在实数空间中，有理数集Q 的边界()Q ∂是（ ）① φ ② Q ③ R -Q ④ R21、在实数空间中，整数集Z 的内部Z 是（ ）① φ ② Z ③ R -Z ④ R22、在实数空间中，整数集Z 的边界()Z ∂是（ ）① φ ② Z ③ R -Z ④ R23、在实数空间中，区间[0,1)的边界是（ ）① φ ② [0,1] ③ {0,1} ④ (0,1)24、在实数空间中，区间[2,3)的边界是（ ）① φ ② [2,3] ③ {2,3} ④ (2,3)25、在实数空间中，区间[0,1)的内部是（ ）① φ ② [0,1] ③ {0,1} ④ (0,1)26、设X 是一个拓扑空间，A ,B 是X 的子集,则下列关系中错误的是（ ） ① ()()()d A B d A d B ⋃=⋃ ② A B A B ⋃=⋃③ ()()()d A B d A d B ⋂=⋂ ④ A A =27、设X 是一个拓扑空间，A ,B 是X 的子集,则下列关系中正确的是（ ） ① ()()()d A B d A d B ⋃=⋃ ② A B A B -=-③ ()()()d A B d A d B ⋂=⋂ ④ A A =28、设X 是一个拓扑空间，A ,B 是X 的子集,则下列关系中正确的是（ ）① ()d A B A B ⋃=⋃ ② A B A B -=-③ ()()()d A B d A d B ⋂=⋂ ④ (())()d d A A d A ⊂⋃29、已知X 是一个离散拓扑空间，A 是X 的子集,则下列结论中正确的是（ ） ① ()d A φ= ② ()d A X A =-③ ()d A A = ④ ()d A X =30、已知X 是一个平庸拓扑空间，A 是X 的子集,则下列结论中不正确的是（ ）① 若A φ=,则()d A φ= ② 若0{}A x =,则()d A X A =-③ 若A={12,x x },则()d A X = ④ 若A X ≠, 则()d A X ≠31、已知X 是一个平庸拓扑空间，A 是X 的子集,则下列结论中正确的是（ ）① 若A φ=,则()d A φ= ② 若0{}A x =,则()d A X =③ 若A={12,x x },则()d A X A =- ④ 若12{,}A x x =,则()d A A =32、设{,,,}X a b c d =，令{{,,},{},{}}a b c c d =B ,则由B 产生的X 上的拓扑是（ ）① { X ,φ,{c },{d },{c ,d },{a ,b ,c }}② {X ,φ,{c },{d },{c ,d }}③ { X ,φ,{c },{a ,b ,c }}④ { X ,φ,{d },{b ,c },{b ,d },{b ,c ,d }}33、设X 是至少含有两个元素的集合，p X ∈,{|}{}G X p G φ=⊂∈⋃T 是X 的拓扑，则（ ）是T 的基.① {{,}|{}}B p x x X p =∈- ② {{}|}B x x X =∈③ {{,}|}B p x x X =∈ ④ {{}|{}}B x x X p =∈-34、 设{,,}X a b c =,则下列X 的拓扑中（ ）以{,,{}}S X a φ=为子基.① { X , φ,{a },{a ,c }} ② {X , φ,{a }}③ { X , φ,{a },{b },{a ,b }} ④ {X ,φ }35、离散空间的任一子集为( )① 开集 ② 闭集 ③ 即开又闭 ④ 非开非闭36、平庸空间的任一非空真子集为( )① 开集 ② 闭集 ③ 即开又闭 ④ 非开非闭37、实数空间R 中的任一单点集是 ( )① 开集 ② 闭集 ③ 既开又闭 ④ 非开非闭38、实数空间R 的子集A ={1,21,31 ,41,……},则A ＝（ ） ①φ ② R ③ A ∪{0} ④ A39、在实数空间R 中，下列集合是闭集的是（ ）① 整数集 ② [)b a , ③ 有理数集 ④ 无理数集40、在实数空间R 中，下列集合是开集的是（ ）① 整数集Z ② 有理数集③ 无理数集 ④ 整数集Z 的补集Z '41、已知{1,2,3}X =上的拓扑{,,{1}}T X φ=,则点1的邻域个数是（ ）① 1 ② 2 ③ 3 ④ 442、已知{,}X a b =,则X 上的所有可能的拓扑有（ ）① 1个 ② 2个 ③ 3个 ④ 4个43、已知X ={a ,b ,c },则X 上的含有４个元素的拓扑有（ ）个① 3 ② 5 ③ 7 ④ 944、设(,)T X 为拓扑空间,则下列叙述正确的为 ( )①T , T X φ∈∉ ② T ,T X φ∉∈③当T T '⊂时,T T U U '∈∈ ④ 当T T '⊂时,T T U U '∈∈45、在实数下限拓扑空间R 中，区间[,)a b 是（ ）① 开集 ② 闭集 ③ 既是开集又是闭集 ④ 非开非闭46、设X 是一个拓扑空间，,A B X ⊂,且满足()d A B A ⊂⊂,则B 是（ ）① 开集 ② 闭集 ③ 既是开集又是闭集 ④ 非开非闭47、设{1,2,3}X =,{,,{1,2},{1,3},{1},{2}}T=X φ是X 的拓扑，{1,2}A =,则X 的子空间A 的拓扑为( )① {,{2},{1,2}}φ=T ② {,,{1},{2},{1,2}}T X φ=③ {,,{1},{2}}T A φ= ④ {,,{1},{2}}T X φ=48、设{1,2,3}X =,{,,{1,2},{1,3},{1},{2}}T=X φ是X 的拓扑，{1,3}A =,则X 的子空间A 的拓扑为( )① {,{1},{3},{1,3}}T φ= ② {,,{1}}T A φ=③ {,,{1},{3},{1,3}}T X φ= ④ {,,{1}}T X φ=49、设{1,2,3}X =,{,,{1,2},{1,3},{1},{2}}T=X φ是X 的拓扑，{2,3}A =,则X 的子空间A的拓扑为( )① {,{3},{2,3}}φ=T ② {,,{2},{3}}T A φ=③ {,,{2},{3},{2,3}}T X φ= ④ {,,{3}}T X φ=50、设{1,2,3}X =,{,,{1,2},{1,3},{1},{2}}T=X φ是X 的拓扑，{1}A =,则X 的子空间A 的拓扑为( )① {,{1}}T φ= ② {,,{1,2}}T A φ=③ {,,{1},{3},{1,3}}T X φ= ④ {,,{1}}T X φ=51、设{1,2,3}X =,{,,{1,2},{1,3},{1},{2}}T=X φ是X 的拓扑，{2}A =,则X 的子空间A 的拓扑为( )① {,{2},{1,2}}T φ= ② {,}T A φ=③ {,,{2}}T X φ= ④ {,,{1,2}}T X φ=52、设{1,2,3}X =,{,,{1,2},{1,3},{1},{2}}T=X φ是X 的拓扑，{3}A =,则X 的子空间A 的拓扑为( )① {,{2},{1,2}}T φ= ② {,{},{1,3}}T X φ=③ {,,{3}}T X φ= ④ {,{3}}T φ=53、设R 是实数空间，Z 是整数集，则R 的子空间Z 的拓扑为（ ）① {,}T Z φ= ② ()T P Z =③ T Z = ④ {}T Z =54、设126X X X X =⨯⨯⨯是拓扑空间126,,,X X X 的积空间.1P 是X 到1X 的投射，则1P 是（ ）① 单射 ② 连续的单射③ 满的连续闭映射 ④ 满的连续开映射55、设126X X X X =⨯⨯⨯是拓扑空间126,,,X X X 的积空间.2P 是X 到2X 的投射，则2P 是（ ）① 单射 ② 连续的单射③ 满的连续闭映射 ④ 满的连续开映射56、设126X X X X =⨯⨯⨯是拓扑空间126,,,X X X 的积空间.3P 是X 到3X 的投射，则3P 是（ ）① 单射 ② 连续的单射③ 满的连续闭映射 ④ 满的连续开映射57、设126X X X X =⨯⨯⨯是拓扑空间126,,,X X X 的积空间.4P 是X 到4X 的投射，则4P 是（ ）① 单射 ② 连续的单射③ 满的连续闭映射 ④ 满的连续开映射58、设126X X X X =⨯⨯⨯是拓扑空间126,,,X X X 的积空间.5P 是X 到5X 的投射，则5P 是（ ）① 单射 ② 连续的单射③ 满的连续闭映射 ④ 满的连续开映射59、设126X X X X =⨯⨯⨯是拓扑空间126,,,X X X 的积空间.6P 是X 到6X 的投射，则6P 是（ ）① 单射 ② 连续的单射③ 满的连续闭映射 ④ 满的连续开映射60、设1X 和2X 是两个拓扑空间，12X X ⨯是它们的积空间,1A X ⊂，2B X ⊂，则有（ ） ① A B A B ⨯≠⨯ ② A B A B ⨯=⨯③()A B A B ⨯≠⨯ ④ ()()()A B A B ∂⨯=∂⨯∂61、有理数集Q 是实数空间R 的一个（ ）① 不连通子集 ② 连通子集③ 开集 ④ 以上都不对62、整数集Z 是实数空间R 的一个（ ）① 不连通子集 ② 连通子集③ 开集 ④ 以上都不对63、无理数集是实数空间R 的一个（ ）① 不连通子集 ② 连通子集③ 开集 ④ 以上都不对64、设Y 为拓扑空间X 的连通子集,Z 为X 的子集,若Y Z Y ⊂⊂, 则Z 为( )①不连通子集 ② 连通子集 ③ 闭集 ④ 开集65、设12,X X 是平庸空间，则积空间12X X ⨯是（ ）① 离散空间 ② 不一定是平庸空间③ 平庸空间 ④ 不连通空间66、设12,X X 是离散空间，则积空间12X X ⨯是（ ）① 离散空间 ② 不一定是离散空间③ 平庸空间 ④ 连通空间67、设12,X X 是连通空间，则积空间12X X ⨯是（ ）① 离散空间 ② 不一定是连通空间③ 平庸空间 ④ 连通空间68、实数空间R 中的连通子集E 为( )① 开区间 ② 闭区间 ③区间 ④ 以上都不对69、实数空间R 中的不少于两点的连通子集E 为( )① 开区间 ② 闭区间 ③ 区间 ④ 以上都不对70、实数空间R 中的连通子集E 为( )① 开区间 ② 闭区间 ③ 区间 ④ 区间或一点71、下列叙述中正确的个数为（ ）（Ⅰ）单位圆周1S 是连通的； （Ⅱ）{0}R -是连通的（Ⅲ）2{(0,0)}R -是连通的 （Ⅳ）2R 和R 同胚① 1 ② 2 ③ 3 ④ 472、实数空间R ( )① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对73、整数集Z 作为实数空间R 的子空间（ ）① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对74、有理数集Q 作为实数空间R 的子空间（ ）① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对75、无理数集作为实数空间R 的子空间（ ）① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对76、正整数集Z +作为实数空间R 的子空间（ ）① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对77、负整数集Z -作为实数空间R 的子空间（ ）① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对78、2维欧氏间空间2R （ ）① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对79、3维欧氏间空间3R （ ）① 仅满足第一可数性公理 ② 仅满足第二可数性公理③ 既满足第一又满足第二可数性公理 ④ 以上都不对80、下列拓扑学的性质中，不具有可遗传性的是（ ）① 平庸性 ② 连通性③ 离散性 ④ 第一可数性公理81、下列拓扑学的性质中，不具有可遗传性的是（ ）① 第一可数性公理 ② 连通性③ 第二可数性公理 ④ 平庸性82、下列拓扑学的性质中，不具有可遗传性的是（ ）① 第一可数性公理 ② 可分性③ 第二可数性公理 ④ 离散性83、下列拓扑学的性质中，不具有可遗传性的是（ ）① 平庸性 ② 可分性③ 离散性 ④ 第二可数性公理84、设X 是一个拓扑空间，若对于,,x y X x y ∀∈≠,均有{}{}x y ≠,则X 是( )① 0T 空间 ② 1T 空间 ③ 2T 空间 ④ 以上都不对85、设{1,2}X =，{,,{1}}X φ=T ，则(,)X T 是( )① 0T 空间 ② 1T 空间 ③ 2T 空间 ④ 以上都不对86、设{1,2}X =，{,,{2}}X φ=T ，则(,)X T 是( )① 0T 空间 ② 1T 空间 ③ 2T 空间 ④ 道路连通空间87、设{1,2,3}X =，{,,{1}}X φ=T ，则(,)X T 是( )① 0T 空间 ② 1T 空间 ③ 2T 空间 ④ 以上都不对88、设{1,2,3}X =，{,,{23}}X φ=，T ，则(,)X T 是( )① 0T 空间 ② 1T 空间 ③ 2T 空间 ④ 以上都不对89、设{1,2,3}X =，{,,{13}}X φ=，T ，则(,)X T 是( )① 0T 空间 ② 1T 空间 ③ 2T 空间 ④ 以上都不对90、设{1,2,3}X =，{,,{12}}X φ=，T ，则(,)X T 是( )① 0T 空间 ② 1T 空间 ③ 2T 空间 ④ 以上都不对91、设{1,2,3}X =，{,,{1},{2},{1,2}}X φ=T ，则(,)X T 是( )①0T 空间 ② 1T 空间 ③ 2T 空间 ④ 以上都不对92、设X 是一个拓扑空间，若X 的每一个单点集都是闭集，则X 是（ ）①正则空间 ②正规空间 ③ 1T 空间 ④ 4T 空间93、设X 是一个拓扑空间，若X 的每一个有限子集都是闭集，则X 是（ ）①正则空间 ②正规空间 ③ 1T 空间 ④ 4T 空间94、设X 是一个拓扑空间，若对x X ∀∈及x 的每一个开邻域U ，都存在x 的一个开邻域V ,使得V U ⊂,则X 是（ ）①正则空间 ②正规空间 ③ 1T 空间 ④ 4T 空间95、设X 是一个拓扑空间，若对X 的任何一个闭集A 及A 的每一个开邻域U ，都存在A的一个开邻域V ,使得V U ⊂,则X 是（ ）①正则空间 ②正规空间 ③ 1T 空间 ④ 4T 空间96、设{1,23}X =，，{,,{1},{23}}X φ=，T ，则(,)X T 是( ) ①0T 空间 ② 1T 空间 ③ 2T 空间 ④ 正规空间97、设{1,23}X =，，{,,{2},{13}}X φ=，T ，则(,)X T 是( ) ①0T 空间 ② 1T 空间 ③ 2T 空间 ④ 正规空间98、设{1,23}X =，，{,,{3},{12}}X φ=，T ，则(,)X T 是( )①0T 空间 ② 1T 空间 ③ 2T 空间 ④ 正则空间99、设{1,23}X =，，{,,{1},{2},{1,2}}X φ=T ，则(,)X T 是( )①2T 空间 ② 正则空间 ③ 4T 空间 ④ 正规空间100、设{1,23}X =，，{,,{1},{3},{1,3}}X φ=T ，则(,)X T 是( )①2T 空间 ② 正则空间 ③ 4T 空间 ④ 正规空间101、设{1,23}X =，，{,,{2},{3},{2,3}}X φ=T ，则(,)X T 是( )①2T 空间 ② 正则空间 ③ 4T 空间 ④ 正规空间102、若拓扑空间X 的每一个开覆盖都有一个有限子覆盖，则称拓扑空间X 是一个（）① 连通空间 ② 道路连通空间 ③ 紧致空间 ④ 可分空间103、紧致空间中的每一个闭子集都是（ ）① 连通子集 ② 道路连通子集 ③ 紧致子集 ④ 以上都不对104、Hausdorff 空间中的每一个紧致子集都是（ ）① 连通子集 ② 开集 ③ 闭集 ④ 以上都不对105、紧致的Hausdorff 空间中的紧致子集是（ ）① 连通子集 ② 开集 ③ 闭集 ④ 以上都不对106、拓扑空间X 的任何一个有限子集都是（ ）① 连通子集 ② 紧致子集 ③ 非紧致子集 ④ 开集107、实数空间R 的子集{1,2,3}A =是（ ）① 连通子集 ② 紧致子集 ③开集 ④ 非紧致子集108、实数空间R 的子集{1,2,3,4}A =是（ ）① 连通子集 ② 紧致子集 ③开集 ④ 非紧致子集109、如果拓扑空间X 的每个紧致子集都是闭集，则X 是（ ）① 1T 空间 ② 紧致空间 ③ 可数补空间 ④ 非紧致空间二、填空题（每题2分）1、设{,}X a b =,则X 的平庸拓扑为 ;2、设{,}X a b =,则X 的离散拓扑为 ;3、同胚的拓扑空间所共有的性质叫 ;4、在实数空间R 中，有理数集Q 的导集是___________.5、)(A d x ∈当且仅当对于x 的每一邻域U 有 ;6、设A是有限补空间X中的一个无限子集，则()d A= ;7、设A是有限补空间X中的一个无限子集，则A= ;8、设A是可数补空间X中的一个不可数子集，则()d A= ;9、设A是可数补空间X中的一个不可数子集，则A= ;10、设{1,2,3}X=,X的拓扑{,,{2},{2,3}}=,则X的子集{1,2}A=的内部T Xφ为 ;11、设{1,2,3}A=的内部=,则X的子集{1,3} X=,X的拓扑{,,{1},{2,3}}T Xφ为 ;12、设{1,2,3}A=的内部=,则X的子集{1,2}T XφX=,X的拓扑{,,{1},{2,3}}为 ;13、设{1,2,3}A=的内部=,则X的子集{1,3} X=,X的拓扑{,,{2},{2,3}}T Xφ为 ;14、设{,,}=,则X的平庸拓扑为 ;X a b c15、设{,,}=,则X的离散拓扑为 ;X a b c16、设{1,2,3}A=的内部=,则X的子集{1,3}T XφX=,X的拓扑{,,{2},{3},{2,3}}为 ;17、设{1,2,3}A=的内部=,则X的子集{1,2}T XφX=,X的拓扑{,,{1},{3},{1,3}}为 ;18、:f X Y→是拓扑空间X到Y的一个映射，若它是一个单射，并且是从X到它的象集()f X的一个同胚，则称映射f是一个 .19、:f X Y→是拓扑空间X到Y的一个映射，如果它是一个满射，并且Y的拓扑是对于映射f而言的商拓扑，则称f是一个 .20、设,→是一个映射，若X中任何一个开集U的象集X Y是两个拓扑空间，:f X Yf U是Y中的一个开集，则称映射f是一个;()21、设,→是一个映射，若X中任何一个闭集U的象集X Y是两个拓扑空间，:f X Y()f U 是Y 中的一个闭集，则称映射f 是一个 ;22、若拓扑空间X 存在两个非空的闭子集,A B ,使得,A B A B X φ⋂=⋃=,则X 是一个 ；23、若拓扑空间X 存在两个非空的开子集,A B ,使得,A B A B X φ⋂=⋃=,则X 是一个 ；24、若拓扑空间X 存在着一个既开又闭的非空真子集，则X 是一个 ；25、设Y 是拓扑空间X 的一个连通子集，Z X ⊂满足Y Z Y ⊂⊂，则Z 也是X 的一个 ;26、拓扑空间的某种性质，如果为一个拓扑空间所具有也必然为它在任何一个连续映射下的象所具有，则称这个性质是一个 ；27、拓扑空间的某种性质，如果为一个拓扑空间所具有也必然为它的任何一个商空间所具有，则称这个性质是一个 ；28、若任意1n ≥个拓扑空间12,,,n X X X ,都具有性质P ,则积空间12n X X X ⨯⨯⨯也具有性质P ，则性质P 称为 ;29、设X 是一个拓扑空间，如果X 中有两个非空的隔离子集,A B ,使得A B X ⋃=,则称X 是一个 ；30、若12,X X 满足第一可数性公理，则积空间12X X ⨯满足 ;31、若12,X X 满足第二可数性公理，则积空间12X X ⨯也满足 ;32、如果一个拓扑空间具有性质P ,那么它的任何一个子空间也具有性质P ,则称性质P为 ;33、设D 是拓扑空间X 的一个子集，且D X =,则称D 是X 的一个 ；34、若拓扑空间X 有一个可数稠密子集，则称X 是一个 ；35、设X 是一个拓扑空间，如果它的每一个开覆盖都有一个可数子覆盖，则称X 是一个 ；36、如果一个拓扑空间具有性质P ,那么它的任何一个开子空间也具有性质P ,则称性质P 为 ;37、如果一个拓扑空间具有性质P ,那么它的任何一个闭子空间也具有性质P ,则称性质P 为 ;38、设X 是一个拓扑空间，如果则称X 是一个0T 空间;39、设X 是一个拓扑空间，如果则称X 是一个1T 空间;40、设X 是一个拓扑空间，如果则称X 是一个2T 空间;41、正则的1T 空间称为 ；42、正规的1T 空间称为 ；43、完全正则的1T 空间称为 ；44、设X 是一个拓扑空间.如果X 的每一个开覆盖都有一个有限子覆盖，则称拓扑空间X 是一个 .45、设X 是一个拓扑空间，Y 是X 的一个子集.如果Y 作为X 的子空间是一个紧致空间，则称Y 是拓扑空间X 的一个 .46、设X 是一个拓扑空间. 如果X 的每一个可数开覆盖都有有限子覆盖，则称拓扑空间X 是一个 .47、设X 是一个拓扑空间. 如果X 的每一个无限子集都有凝聚点，则称拓扑空间X 是一个 .48、设X 是一个拓扑空间. 如果X 中的每一个序列都有一个收敛的子序列，则称拓扑空间X 是一个 .三．判断（每题3分，判断1分，理由2分）1、从离散空间到拓扑空间的任何映射都是连续映射( )2、设12, T T 是集合X 的两个拓扑，则12 T T ⋂不一定是集合X 的拓扑( )3、从拓扑空间X 到平庸空间Y 的任何映射都是连续映射（ ）4、设A 为离散拓扑空间X 的任意子集，则()d A φ= （ ）5、设A 为平庸空间X （X 多于一点）的一个单点集，则()d A φ= （ ）6、设A 为平庸空间X 的任何一个多于两点的子集，则()d A X = （ ）7、设X 是一个不连通空间，则X 中存在两个非空的闭子集,A B ,使得,A B A B X φ⋂=⋃=（ ）8、若拓扑空间X 中存在一个既开又闭的非空真子集，则X 是一个不连通空间( )9、设拓扑空间X 满足第二可数性公理，则X 满足第一可数性公理（ ）10、若拓扑空间X 满足第二可数性公理，则X 的子空间Y 也满足第二可数性公理（ ）11、若拓扑空间X 满足第一可数性公理，则X 的子空间Y 也满足第一可数性公理（ ）12、设{1,2,3}X =，{,,{2},{3},{2,3}}X φ=T ，则(,)X T 是3T 空间.( )13、设{1,2,3}X =，{,,{1},{2},{1,2}}T X φ=，则(,)X T 是3T 空间.( )14、设{1,23}X =，，{,,{1},{3},{1,3}}X φ=T ，则(,)X T 是1T 空间.( )15、设{1,23}X =，，{,,{1},{3},{1,3}}X φ=T ，则(,)X T 是4T 空间.( )16、3T 空间一定是2T 空间.（ ）17、4T 空间一定是3T 空间.（ ）18、设,A B 是拓扑空间X 的两个紧致子集，则A B ⋃是一个紧致子集.( )19、Hausdorff 空间中的每一个紧致子集都是闭集.( )四．名词解释(每题2分)1．同胚映射2、集合A 的内点3、集合A 的内部4．拓扑空间(,)T X 的基5．闭包6、序列7、导集8、不连通空间9、连通子集10、不连通子集11、1 A 空间12、2 A 空间13、可分空间14、0T 空间：15、1T 空间：16、2T 空间：17、正则空间：18、正规空间：19、完全正则空间：20、紧致空间21、紧致子集22、可数紧致空间23、列紧空间24、序列紧致空间五．简答题（每题4分）1、设X 是一个拓扑空间，,A B 是X 的子集，且A B ⊂.试说明()()d A d B ⊂.2、设,,X Y Z 都是拓扑空间.:f X Y →, :g Y Z →都是连续映射，试说明:g f X Z →也是连续映射.3、设X 是一个拓扑空间，A X ⊂.试说明：若A 是一个闭集，则A 的补集A '是一个开集.4、设X 是一个拓扑空间，A X ⊂.试说明：若A 的补集A '是一个开集，则A 是一个闭集.5、在实数空间R 中给定如下等价关系：~x y ⇔)1,(,-∞∈y x 或者)2,1[,∈y x 或者),2[,+∞∈y x设在这个等价关系下得到的商集]}2[],1[],0{[=Y ,试写出Y 的商拓扑T .6、在实数空间R 中给定如下等价关系:~x y ⇔]1,(,-∞∈y x 或者]2,1(,∈y x 或者),2(,+∞∈y x设在这个等价关系下得到的商集]}3[],2[],1{[=Y ,试写出Y 的商拓扑T .7、在实数空间R 中给定如下等价关系：~x y ⇔)1,(,-∞∈y x 或者)2,1[,∈y x 或者),2[,+∞∈y x设在这个等价关系下得到的商集{[1],[1],[2]}Y =-,试写出Y 的商拓扑T .8、在实数空间R 中给定如下等价关系：~x y ⇔)1,(,-∞∈y x 或者)2,1[,∈y x 或者),2[,+∞∈y x设在这个等价关系下得到的商集{[2],[1],[2]}Y =-,试写出Y 的商拓扑T .9、在实数空间R 中给定如下等价关系:~x y ⇔]1,(,-∞∈y x 或者]2,1(,∈y x 或者),2(,+∞∈y x设在这个等价关系下得到的商集{[0],[2],[3]}Y =,试写出Y 的商拓扑T .10、在实数空间R 中给定如下等价关系:~x y ⇔]1,(,-∞∈y x 或者]2,1(,∈y x 或者),2(,+∞∈y x设在这个等价关系下得到的商集{[0],[2],[4]}Y =,试写出Y 的商拓扑T .11、在实数空间R 中给定如下等价关系:~x y ⇔]1,(,-∞∈y x 或者]2,1(,∈y x 或者),2(,+∞∈y x设在这个等价关系下得到的商集{[1],[2],[4]}Y =-,试写出Y 的商拓扑T .12、离散空间是否为2A 空间?说出你的理由.13、试说明实数空间R 是可分空间.14、试说明每一个度量空间都满足第一可数性公理.15、设X 是一个1T 空间，试说明X 的每一个单点集是闭集.16、设X 是一个拓扑空间，若X 的每一个单点集都是闭集，试说明X 是一个1T 空间.17、设(,)X T 是一个1T 空间，∞是任何一个不属于X 的元素.令*{}X X =⋃∞和*X =⋃*T T {}，试说明拓扑空间*(,)X *T 是一个0T 空间.18、若X 是一个正则空间，试说明：对x X ∀∈及x 的每一个开邻域U ，都存在x 的一个开邻域V ,使得V U ⊂.19、若X 是一个正规空间，试说明：对X 的任何一个闭集A 及A 的每一个开邻域U ，都存在A 的一个开邻域V ,使得V U ⊂.20、试说明1T 空间X 的任何一个子集的导集都是闭集.21、试说明紧致空间X 的无穷子集必有凝聚点.22、如果X Y ⨯是紧致空间，则X 是紧致空间.23、如果X Y ⨯是紧致空间，则Y 是紧致空间.24、试说明紧致空间X 的每一个闭子集Y 都是紧致子集.六、证明题（每题8分）1、设:f X Y →是从连通空间X 到拓扑空间Y 的一个连续映射.则()f X 是Y 的一个连通子集.2、设Y 是拓扑空间X 的一个连通子集, 证明: 如果A 和B 是X 的两个无交的开集使得B A Y ⋃⊂,则或者A Y ⊂,或者B Y ⊂.3、设Y 是拓扑空间X 的一个连通子集, 证明: 如果A 和B 是X 的两个无交的闭集使得B A Y ⋃⊂,则或者A Y ⊂,或者B Y ⊂.4、设Y 是拓扑空间X 的一个连通子集，Z X ⊂满足Y Z Y ⊂⊂，则Z 也是X 的一个连通子集.5、设{}Y γγ∈Γ是拓扑空间X 的连通子集构成的一个子集族.如果Y γγφ∈Γ≠,则Y γγ∈Γ是X 的一个连通子集.6、设A 是拓扑空间X 的一个连通子集，B 是X 的一个既开又闭的集合.证明：如果A B φ⋂≠,则A B ⊂.7、设A 是连通空间X 的非空真子集. 证明:A 的边界()A φ∂≠.8、设X 是一个含有不可数多个点的可数补空间.证明X 不满足第一可数性公理.9、设X 是一个含有不可数多个点的有限补空间.证明:X 不满足第一可数性公理.10、设,X Y 是两个拓扑空间，:f X Y →是一个满的连续开映射.X 满足第二可数性公理，证明：Y 也满足第二可数性公理.11、设,X Y 是两个拓扑空间，:f X Y →是一个满的连续开映射.X 满足第一可数性公理，证明：Y 也满足第一可数性公理.12、A 是满足第二可数性公理空间X 的一个不可数集。

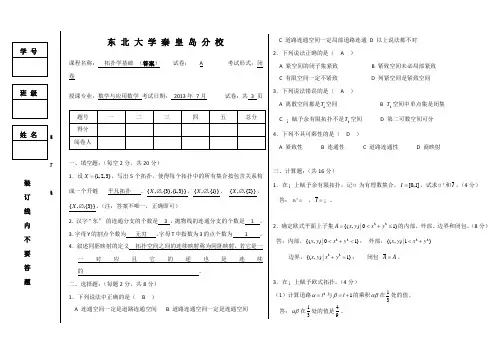
东 北 大 学 秦 皇 岛 分 校课程名称： 拓扑学基础 （答案） 试卷： A 考试形式：闭卷授课专业：数学与应用数学 考试日期： 2013年 7月 试卷：共 3 页一、填空题：（每空2分，共20分）1．设{1,2,3}X =，写出5个拓扑，使得每个拓扑中的所有集合按包含关系构成一个升链 平凡拓扑 ，{,,{3},{1,3}}X ∅，{,,{1}}X ∅， {,,{2}}X ∅，{,,{3}}X ∅。

（注：答案不唯一，正确即可）2. 汉字“东” 的连通分支的个数是 3 ，抛物线的连通分支的个数是 1 。

3．字母Y 的割点个数为 无穷 。

字母T 中指数为3的点个数为 1 。

4．叙述同胚映射的定义 拓扑空间之间的连续映射称为同胚映射，若它是一一对应且它的逆也是连续的 。

二、选择题：（每题2分，共8分） 1．下列说法中正确的是（ B ）A 连通空间一定是道路连通空间B 道路连通空间一定是连通空间C 道路连通空间一定局部道路连通D 以上说法都不对 2．下列说法正确的是（ A ）A 紧空间的闭子集紧致B 紧致空间未必局部紧致C 有限空间一定不紧致D 列紧空间是紧致空间 3．下列说法错误的是（ A ）A 离散空间都是1T 空间B 2T 空间中单点集是闭集C ¡赋予余有限拓扑不是2T 空间D 第二可数空间可分 4．下列不具可乘性的是（ D ）A 紧致性B 连通性C 道路连通性D 商映射三、计算题：（共16分）1．在¡上赋予余有限拓扑，记¤为有理数集合，[0,1]I =。

试求'¤和I 。

（4分） 答：'=ぁ，I =¡。

2．确定欧式平面上子集22{(,)|01}A x y x y =<+≤的内部、外部、边界和闭包。

（8分）答：内部，22{(,)|01}x y x y <+<； 外部，22{(,)|1}x y x y <+ 边界，22{(,)|1}x y x y +=； 闭包 A A =。

东 北 大 学 秦 皇 岛 分 校课程名称： 拓扑学基础 （答案） 试卷： A 考试形式：闭卷授课专业：数学与应用数学 考试日期： 2013年 7月 试卷：共 3 页一、填空题：（每空2分，共20分）1．设{1,2,3}X =，写出5个拓扑，使得每个拓扑中的所有集合按包含关系构成一个升链 平凡拓扑 ，{,,{3},{1,3}}X ∅，{,,{1}}X ∅， {,,{2}}X ∅，{,,{3}}X ∅。

（注：答案不唯一，正确即可）2. 汉字“东” 的连通分支的个数是 3 ，抛物线的连通分支的个数是 1 。

3．字母Y 的割点个数为 无穷 。

字母T 中指数为3的点个数为 1 。

4．叙述同胚映射的定义 拓扑空间之间的连续映射称为同胚映射，若它是一一对应且它的逆也是连续的 。

二、选择题：（每题2分，共8分） 1．下列说法中正确的是（ B ）A 连通空间一定是道路连通空间B 道路连通空间一定是连通空间C 道路连通空间一定局部道路连通D 以上说法都不对 2．下列说法正确的是（ A ）A 紧空间的闭子集紧致B 紧致空间未必局部紧致C 有限空间一定不紧致D 列紧空间是紧致空间 3．下列说法错误的是（ A ）A 离散空间都是1T 空间B 2T 空间中单点集是闭集C ¡赋予余有限拓扑不是2T 空间D 第二可数空间可分 4．下列不具可乘性的是（ D ）A 紧致性B 连通性C 道路连通性D 商映射三、计算题：（共16分）1．在¡上赋予余有限拓扑，记¤为有理数集合，[0,1]I =。

试求'¤和I 。

（4分） 答：'=ぁ，I =¡。

2．确定欧式平面上子集22{(,)|01}A x y x y =<+≤的内部、外部、边界和闭包。

（8分）答：内部，22{(,)|01}x y x y <+<； 外部，22{(,)|1}x y x y <+ 边界，22{(,)|1}x y x y +=； 闭包 A A =。

拓扑学基础试题及答案一、选择题（每题2分，共10分）1. 拓扑空间中，以下哪个概念不是基本的？A. 开集B. 闭集C. 连续函数D. 距离函数答案：D2. 以下哪个选项不是拓扑空间的性质？A. 空集和整个空间是开集B. 任意开集的并集是开集C. 有限个开集的交集是开集D. 任意集合的补集是闭集答案：D3. 在拓扑学中，两个拓扑空间之间的映射被称为？A. 同胚B. 连续映射C. 同伦D. 同调答案：B4. 拓扑空间中的邻域系统是指？A. 包含某点的所有开集的集合B. 包含某点的任意集合的集合C. 包含某点的有限个开集的交集D. 包含某点的任意开集答案：A5. 拓扑空间中的连通性是指？A. 空间不能被分割成两个不相交的非空开集B. 空间中的任意两点都可以通过连续路径相连C. 空间中的任意两点都可以通过直线相连D. 空间中的任意两点都可以通过曲线相连答案：A二、填空题（每题3分，共15分）1. 如果拓扑空间中任意两个不同的点都存在不相交的邻域，则称该空间为________。

答案：豪斯多夫空间2. 拓扑空间中的紧致性是指该空间的任意开覆盖都有________。

答案：有限子覆盖3. 拓扑空间中的连通空间是指不能表示为两个不相交的非空开集的并集的空间，这种性质也称为________。

答案：不可分割性4. 拓扑空间中的基是指由开集构成的集合，使得空间中的每一个开集都可以表示为基中集合的________。

答案：并集5. 拓扑空间中的同胚是指两个拓扑空间之间存在一个双射的连续映射，并且其逆映射也是连续的，这种映射也称为________。

答案：同胚映射三、简答题（每题10分，共20分）1. 请简述拓扑空间中闭集的定义。

答案：在拓扑空间中，如果一个集合的补集是开集，则称该集合为闭集。

2. 请解释什么是拓扑空间中的同伦等价。

答案：如果存在两个拓扑空间之间的连续映射，使得这两个映射的复合与各自空间上的恒等映射是同伦的，则称这两个空间是同伦等价的。