当前位置：文档之家 › 第二章 线性时不变系统的时域分析

第二章 线性时不变系统的时域分析

  • 格式：ppt
  • 大小：229.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

信号与系统第二章_线性时不变系统

信号与系统第二章_线性时不变系统




x(k)h(n k) ku(k)u(n k)
k
k
n k 1 n1 u(n)
k 0
1
11
例2：
x(n)

1 0
0n4 otherwise
n
h(n) 0
1,0 n 6
otherwise

h(t) h(n)
x(t)
y(t) y(n)
结论：
一个单位冲激响应是 h(t) 的LTI系统对输入 信号 x(t) 所产生的响应，与一个单位冲激响应 是x(t)的LTI系统对输入信号 h(t) 所产生的响应
相同。
25
2. 分配律： x(n) [h1(n) h2 (n)] x(n) h1(n) x(n) h2(n) x(t) [h1(t) h2 (t)] x(t) h1(t) x(t) h2(t)
1
本章主要内容：
• 信号的时域分解——用 (n) 表示离散时间信号； 用 (t) 表示连续时间信号。
• LTI系统的时域分析——卷积积分与卷积和。
• LTI系统的微分方程及差分方程表示。 • LTI系统的框图结构表示。 • 奇异函数。
2
2.0 引言 ( Introduction )
由于LTI系统满足齐次性和可加性，并且具有 时不变性的特点，因而为建立信号与系统分析的 理论与方法奠定了基础。
缺点：①只适用于两个有限长序列的卷积和； ②一般情况下，无法写出 y(n)的封闭表达式。
15
2.2 连续时间LTI系统：卷积积分
（Continuous-Time LTI Systems:The convolution integral）
控制工程基础第二章控制系统的时域分析

控制工程基础第二章控制系统的时域分析


2.2线性系统的时域性能指标
为了评价线性系统的时间响应的性能，需要研究其在典型输入信号 作用下的时间响应过程。在典型输入信号的作用下，控制系统的时间响 应分为动态过程和稳态过程两部分。
动态过程又称为过渡过程或瞬态过程，是指系统在典型输入信号作 用下，其输出量从初始状态到最终状态的响应过程。根据系统结构和参 数的选择情况，动态过程表现为衰减、发散或等幅振荡的形式。显然， 一个实际运行的系统其动态过程必须是衰减的，也就是说，系统必须是 稳定的。动态过程除提供系统稳定的信息外，还可以提供其相应速度和 阻尼情况等信息，这些特性用动态性能指标描述。
控制系统的单位阶跃响应常用h(t)表示，单位阶跃响应曲线及 时域性能指标如图2-2所示。
图2-2 单位阶跃响应曲线及时域性能指标
（1）延迟时间 td。响应曲线第一次达到稳态值的一半所需的时间 称为延迟时间。 （2）上升时间 tr。上升时间是响应曲线从稳态值的10%上升到90%所 需的时间；或从0上升到100%所需的时间。对于欠阻尼二阶系统，通 常采用0~100%的上升时间；对于过阻尼系统，通常采用10%~90%的 上升时间。上升时间越短，响应速度越快。 （3）峰值时间tp。响应曲线达到超调量的第一个峰值所需要的时间称 为峰值时间。 （4）调节时间ts。调节时间是在响应曲线的稳态线上，用稳态值的百 分数（通常Δ取5%或2%）做一个允许误差范围，响应曲线达到并永远 保持在这一允许误差范围内所需的时间。 （5）最大超调量Mp。最大超调量指响应的最大偏离量h(tp)与终值h(∞ )之差的百分比，用σ%表示：
所谓时域分析法，就是在时域内通过拉氏变换求解系统的微分方 程，得到系统的时间响应，根据相应表达式和相应曲线分析系统的稳 定性、稳态误差等指标。
本章主要介绍时域响应及典型的输入信号；一阶、二阶系统的时 间响应；高阶系统的时间响应及主导极点、偶极子及高阶系统的降阶 方法；稳态误差的概念和计算方法，以及提高系统稳态精度的方法。
系统的时域分析 线性时不变系统的描述及特点 连续时间LTI系统的响应

系统的时域分析 线性时不变系统的描述及特点 连续时间LTI系统的响应

s1 2，s2 3
y x (t ) K1e 2t K 2 e 3t
y(0)=yx(0)=K1+K2=1 y' (0)= y'x(0)= 2K13K2 =3
解得 K1= 6，K2= 5
y x (t ) 6e 2t 5e 3t , t 0
18
[例] 已知某线性时不变系统的动态方程式为: y" (t)+4y ' (t) +4y (t) = 2f ' (t )+3f(t), t>0 系统的初始状态为y(0) = 2，y'(0) = 1， 求系统的零输入响应yx(t)。 解: 系统的特征方程为 系统的特征根为
2t
Be
4t
1 y (0) A B 1 3 解得 A=5/2，B= 11/6 1 y ' (0) 2 A 4 B 2 3
5 2t 11 4t 1 t y(t ) e e e , t 0 2 6 3
12
1 t e 3
系统的几个概念：
9
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et u(t)， 求系统的完全响应y(t)。
解:
(1) 求齐次方程y''(t)+6y'(t)+8y(t) = 0的齐次解yh(t)
11
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
信号与系统王明泉版本~第二章习题解答

信号与系统王明泉版本~第二章习题解答

第2章 线性时不变连续系统的时域分析2.1 学习要求（1）会建立描述系统激励与响应关系的微分方程；（2）深刻理解系统的完全响应可分解为：零输入响应与零状态响应，自由响应与强迫响应，瞬态响应与稳态响应；（3）深刻理解系统的零输入线性与零状态线性，并根据关系求解相关的响应； （4）会根据系统微分方程和初始条件求解上述几种响应； （5）深刻理解单位冲激响应的意义，并会求解；（6）深刻理解系统起始状态与初始状态的区别，会根据系统微分方程和输入判断0时刻的跳变情况； （7）理解卷积运算在信号与系统中的物理意义和运算规律，会计算信号的卷积。

； 2.2 本章重点（1）系统（电子、机械）数学模型（微分方程）的建立； （2）用时域经典法求系统的响应； （3）系统的单位冲激响应及其求解；（4）卷积的定义、性质及运算，特别是()t δ函数形式与其它信号的卷积； （5）利用零输入线性与零状态线性，求解系统的响应。

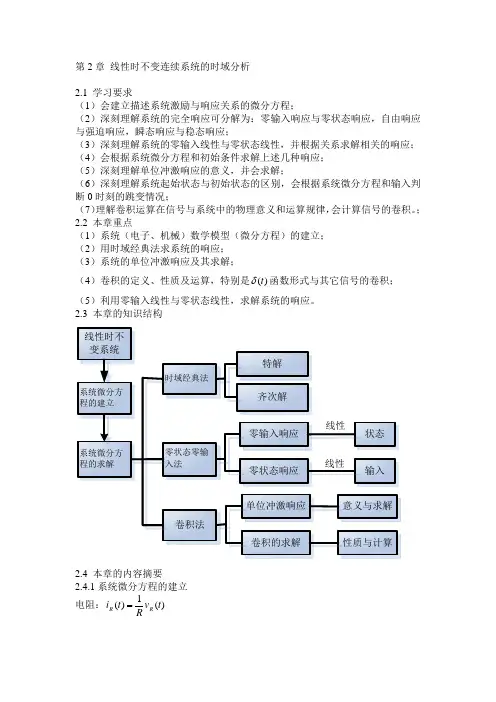
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻：)(1)(t v Rt i R R =电感：dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容：dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。

齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时，如1λ有k 重根，则响应于1λ的重根部分将有k 项，形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根，即bi a +=2,1λ，则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根，即共有m 重ib a ±=2,1λ的复根，则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。

§2-1 LTI系统的零状态响应

§2-1 LTI系统的零状态响应

1
1 2
x(τ)
1 −1 0 1
τ
τ2 t2 1 当1<t<2 y (t ) = ∫ (t − τ + 1)dτ = (tτ − + τ) t −1 = 2 − 2 2 t −1
∞
h(t − τ)
1
t − 10 t
1
t +1
τ
当t>2
y (t ) =
−∞
∫ x(τ)h(t − τ)dτ = 0
h(t − τ)
−∞
u (t − τ ) d τ
1
0
1
u (−τ)
以上积分式的积分的上下限为(1~t)，积 分结果的定义区间为(1~∞)，所以后面要乘 分结果的定义区间为(1~ (1~∞ 以u(t-1)。
t t
1
0
t =0
τ
u (t − τ)
1 t <1 0 t
y 2 (t ) = − ∫ e − ( t − τ ) d τ = − e − t ∫ e τ d τ
大连海事大学信息科学技术学院
《信号与系统》 信号与系统》
∞ ∞
第二章
LTI系统的时域分析 LTI系统的时域分析
y (t ) =
=
−∞ ∞
∫ x ( τ ) h (t − τ ) d τ =
−(t − τ)
−∞
u ( τ ) e − ( t − τ ) u (t − τ ) d τ ∫
u (τ)
1
0
x (t ) = u (t )
,
h (t ) = e − t u (t )
求系统的零状态响应 解：
y (t ) = x (t ) ∗ h (t )
信号与系统第二章小结

信号与系统第二章小结

信号与系统第二章 连续时不变系统的时域分析小结一、系统的初始条件)()()(t y t y t y zs zi +=，令-=0t 和+=0t ，可得)0()0()0(---+=zs zi y y y)0()0()0(++++=zs zi y y y对于因果系统，由于激励在0=t 时接入，故有0)0(=-zs y ；对于时不变系统,内部参数不随时间变化，故有)0()0(+-=zi zi y y 。

因此)0()0()0(+--==zi zi y y y)0()0()0(+-++=zs y y y同理)0()0()0()()()(+--==zi j zi j j y y y)0()0()0()()()(+-++=zs j j j y y y对于n 阶系统,分别称)1,,1,0)(0()(-=-n j y j 和)1,,1,0)(0()(-=+n j y j 为系统的-0和+0初始条件。

二、零输入响应)()()()()(01110111p D p N a p a p a p b p b p b p b t f t y p H n n n m m m m =++++++++==---- )(t y zi 满足算子方程0)()(=t y p D zi ，0≥t即零输入响应)(t y zi 是齐次算子方程满足-0初始条件的解。

)(t y zi 的函数形式与齐次解的形式相同。

简单系统的零输入响应1、)()()(t ce t y p p D t zi ελλ-=⇒+=2、)()()()()(102t e t c c t y p p D t zi ελλ-+=⇒+=三、单位冲激响应)()()(t ke t h p k p H t ελλ-=⇒+= )()()(t k t h kp p H δ'=⇒=)()()(t k t h k p H δ=⇒=)()()()(t kte t h p k p H t ελλ-=⇒+= 四、零状态响应)()()(t h t f t y zs *=五、完全响应)()()(t y t y t y zs zi +=六、卷积1、定义：⎰∞∞--⋅=*τττd t f f t f t f )()()()(21212、性质：交换律：)()()()(1221t f t f t f t f *=*结合律：)()]()([)]()([)(321321t f t f t f t f t f t f **=**分配律：)()()()()]()([)(3121321t f t f t f t f t f t f t f *+*=+*时移性质：)()()(21t y t f t f =*,则)()()()()(0201021t t y t f t t f t t f t f -=*-=-*3、常用信号的卷积公式 )()()(t f t t f =*δ)()()(t f t t f '='*δ)()()()1(t f t t f -=*ε)()()(t t t t εεε=*)()1(1)()(t e at e t at at εεε---=* 七、例题例1已知某连续系统的微分方程为)(3)(2)(2)(3)(t f t f t y t y t y +'=+'+''若系统的初始条件1)0()0(='=--y y ,输入)()(t e t f t ε-=,求)(t y zi ，)(t y zs ,)(t y 。

信号与系统课件

信号与系统课件


u[n] d [m]
mn
d [m]
n
n-k=m
7
离散LTI系统的时域分析—单位脉冲响应与卷积和（1）
利用单位脉冲响应h[n]求离散系统对输入信号x[n]的响应y[n]
（1）单位脉冲响应
x[n]
δ[n]
δ[n-n0]
LTI x[n] y[n]

x[n]
LTI
y[n]
(4) n>6, n–46, 即6<n 10
k
n-4
n
a n4 a 7 y[n] a 1 a k n4

6
k
注：也可以将x[n]分解成d[n]的5项移位线性组合，输出就变成了h[n]的移位线性组合
n 例2-4 x[n] u[n] u[n 5] h[n] a {u[n] u[n 7]}, a 1 求 y[n] x[n] h[n]
10
离散LTI系统的时域分析—单位脉冲响应与卷积和（4）
（4）卷积和的图示求解 1）自变量变换及翻转
x[n] * h[n]
k
x[k ]h[n k ]

x[n] x[k ]
h[n] h[k ] h[k ]
2）平移：将h[-k]随自变量n平移得h[n-k] n>0时，h[-k]向右平移n ； 3）相乘(同一k) ：x[k]h[n-k] 4）求和：将相乘后的x[k]h[n-k]各点相加，即
3
本章主要内容
(1) 离散时间LTI系统的时域分析：卷积和，卷积性质 (2) 连续时间LTI系统的时域分析：卷积积分，卷积性质
(3) 单位冲激/脉冲响应与LTI系统的基本性质
(4) LTI系统的微分、差分方程描述 (5) 系统的响应分解：零输入、零状态响应 (6) 用微分方程、差分方程表征的LTI系统的框图表示
第二章 线性时不变系统

第二章 线性时不变系统

利用多项式算法求卷积和的逆运算 已知 y[n] h[n] x[n] 已知 y[n] x[n] h[n]
9
例5 y[n] 6,5,24,13,22,10,n 0,1,2,3,4,5 h[n] 3,1,4,2 n 0,1,2,3
y[n] x[n]h[n] 求 x[n]
2 t 5t2 x(t)
x[n] x[k] [n k] 离散的信号分解成脉冲
k
信号的 线性组合的形式
把任意一个序列表示成一串移位的单位脉冲序列 [n k]
的线性组合，而这个线性组合式中的权因子就是 x[k]
4
二. 离散时间线性时不变系统卷积和表示
[n] h[n]
[n k] h[n k]
时不变
x[k] [n k] x[k]h[n k] 齐次性
11
二. 连续时间线性时不变系统的卷积积分表示
(t) h (t)
(t k)
x(k) (t k)
x(k) (t k)
k
h (t k)
时不变
x(k
)h
(t
k
)
齐次性
x(k)h (t k) 可加性
k
xˆ(t)
yˆ (t )
y(t) x( )h(t )d x(t) h(t)
12
卷积的计算
（1）由定义计算卷积积分
例：设某一线性时不变系统的输入为x(t)，其单位冲
激响应为h(t) x(t) eatu(t) , a 0 h(t) u(t)
试求 x(t) h(t)
x(t) h(t) ea u( )u(t )d
t ea d ,
0
t0
0,
t0
1 1 eat u(t) a
1
线性时不变系统--习题

线性时不变系统--习题


dt
dt
dt
et t et t
t t t
t
方法二没有注意利用冲激函数的性质，求解过
程较繁。另外，对冲激偶信号的性质
f t t f 0 t f 0 t
往往被错误写成
f t t f 0 t
从而得出错误结论。
(2) f t t e3 δτ d τ
1 O t 3 1
t
t 3 1
t
3
1
即2 t 4
g(t) 1 1(t )d t 2 t 2
t3 2
42
T4
1 f1
f2 t
t
1 O
1 t3
t-31
即t 4
gt 0
卷积结果
f1t
1
1 O 1 t
f2 t
3
2
O
3t
t2 t 1
g(t
)
4 t
t
2
2
4
x(t t0 ) h(t) x(t) h(t t0 ) y(t t0 )
例1 粗略绘出下列各函数式的波形图
(1) f1t u t2 1
(2)
f2 t
d dt
et cos tut
描绘信号波形是本课程的一项基本训练，在绘 图时应注意信号的基本特征，对所绘出的波形，应标 出信号的初值、终值及一些关键的值，如极大值和极 小值等，同时应注意阶跃、冲激信号的特点。
设x3(t) ax1 t bx2 t x3 t y3 t x32 t ax1 t bx2 t 2 a2 x12 t b2 x22 t 2abx1 t x2 t
a2 y1 t b2 y2 t 2abx1 t x2 t ay1 t by2 t
第2章__线性时不变系统

第2章__线性时不变系统

dg (t ) h(t ) dt
g (t ) u(t ) h(t ) h()d
求系统零状态响应举例：如图所示系统， hD (t ) (t 1 ) hG (t ) u(t ) u(t 3) ， ，输入 x(t ) u(t ) u (t 1)，求零状态响应y（t）

k
h[k ]x[n k ]

2、分配律
x[n] (h1[n] h2 [n]) x[n] h1[n] x[n] h2 [n]
x(t ) (h1 (t ) h2 (t )) x(t ) h1 (t ) x(t ) h2 (t )
物理意义： （1）LTI系统对两个输入的和的响应等于对 单个输入响应的和
y[n]
k
x[k ]h [n]
k

• 若该线性系统又是时不变的 ，则有
hk [n] h[n k ]
其中h[n]是系统输入为δ[n]时的零状态响应, 称为单位脉冲(样本)(序列)响应 y[n] x[k ]h[n k ] 所以对LTI系统,有 ： k 对照卷积的定义，有： y[n] x[n] h[n] 称为卷积和
通信中的编码器都是可逆的 例： y(t ) 2 x(t ) w(t ) 1 y(t )
2
y[n]
k
x[k ]
n
w[n] y[n] y[n 1]
不可逆：
y[n] c
y(t ) x (t )
2
2.2.3 因果性
因果系统 ：系统在任何时刻的输出只决定于现在 的输入以及过去的输入
y (t )
因此当 h(t ) dt 时，输出为有界-充分性 亦可证必要性 h(t ) dt 连续时间LTI系统的稳定性 离散时间LTI系统的稳定性 h[n]
自动控制原理实验报告《线性控制系统时域分析》

自动控制原理实验报告《线性控制系统时域分析》

自动控制原理实验报告《线性控制系统时域分析》一、实验目的1. 理解线性时间不变系统的基本概念，掌握线性时间不变系统的数学模型。

2. 学习时域分析的基本概念和方法，掌握时域分析的重点内容。

3. 掌握用MATLAB进行线性时间不变系统时域分析的方法。

二、实验内容本实验通过搭建线性时间不变系统，给出系统的数学模型，利用MATLAB进行系统的时域测试和分析，包括系统的时域性质、单位脉冲响应、单位阶跃响应等。

三、实验原理1. 线性时间不变系统的基本概念线性时间不变系统（Linear Time-Invariant System，简称LTI系统）是指在不同时间下的输入信号均可以通过系统输出信号进行表示的系统，它具有线性性和时不变性两个重要特性。

LTI系统的数学模型可以表示为：y(t) = x(t) * h(t)其中，y(t)表示系统的输出信号，x(t)表示系统的输入信号，h(t)表示系统的冲激响应。

2. 时域分析的基本概念和方法时域分析是一种在时间范围内对系统进行分析的方法，主要涉及到冲激响应、阶跃响应、单位脉冲响应等方面的内容。

针对不同的输入信号，可以得到不同的响应结果，从而确定系统的时域特性。

四、实验步骤与结果1. 搭建线性时间不变系统本实验中，实验者搭建了一个简单的一阶系统，系统的阻尼比为0.2，系统时间常数为1。

搭建完成后，利用信号发生器输出正弦信号作为系统的输入信号。

2. 获取系统的响应结果利用MATLAB进行系统的时域测试和分析，得到了系统的冲激响应、单位阶跃响应和单位脉冲响应等结果。

其中，冲激响应、阶跃响应和脉冲响应分别如下所示：冲激响应：h(t) = 0.2e^(-0.2t) u(t)阶跃响应：H(t) = 1-(1+0.2t) e^(-0.2t) u(t)脉冲响应：g(t) = h(t) - h(t-1)3. 绘制响应图表通过绘制响应图表，可以更好地展示系统的时域性质。

下图展示了系统的冲激响应、阶跃响应和脉冲响应的图表。

2 线性时不变系统的时域分析


于是特解为 全解为：
yp (t) et
y(t) yh (t) yp (t) C1e2t C2e3t et
其中待定常数C1,C2由初始条件确定。 y(0) = C1+C2+ 1 = 2， y’(0) = – 2C1 – 3C2 – 1= – 1
解得 C1 = 3 ，C2 = – 2
最后得全解
解: (1) 特征方程为 2 + 5λ+ 6 = 0 其特征根λ1= – 2，λ2= – 3。 齐次解为 yh (t) C1e2t C2e3t
由表2-2可知，当f(t) = 2 et 时，其特解可设为
yp (t) Pet
将其代入微分方程得 Pet 5(Pet ) 6Pet 2et 解得 P=1
uc
1.5 (t)
即：duc dt
2uc
3 (t)
由于冲激函数是在t=0时给系统注入了一定的能 量，而在t>0时，系统的激励为0。相当于在0－到 0＋时刻，使系统具有了一定的初始能量。因此， 系统的冲激响应与系统的零输入响应具有相同的 形式。这里，用h(t)表示系统的冲激响应。即：
h(t) L[{0}, (t)] cetu(t)的形式。
全响应＝齐次解(自由响应)＋特解(强迫响应)
齐次解：写出特征方程，求出特征根（自然频率或固有频 率）。根据特征根的特点，齐次解有不同的形式。一般形式
（无重根）：
n
rh (t) Cieit i 1
i 为特征根
特解：根据输入信号的形式有对应特解的形式，用待定系数 法确定。在输入信号为直流和正弦信号时，特解就是稳态解。
（5）卷积的积分：
t
t
t
( f (t) h(t)) f (t) h(t) f (t) h(t)

线性系统时域分析实验报告

线性系统时域分析实验报告1. 实验目的本实验旨在通过对线性系统的时域分析，加深对线性系统特性的理解和掌握。

2. 实验原理线性系统是指满足叠加性和比例性质的系统。

时域分析是通过观察系统对不同输入信号的响应来研究系统的特性。

在本实验中，我们将研究线性时不变系统（LTI）在时域上的特性，包括冲激响应和单位阶跃响应。

3. 实验步骤3.1 实验准备准备如下实验设备和材料：•示波器•函数发生器•电阻、电容等元件•连接线3.2 实验步骤1.搭建线性系统电路。

根据实验要求选择合适的电路结构，包括电阻、电容等元件。

将信号源（函数发生器）连接到输入端，示波器连接到输出端。

2.设置函数发生器和示波器。

根据实验要求，设置函数发生器以产生不同类型的输入信号，如方波、正弦波等。

调整示波器的时间和电压刻度，以便能够清晰地观察到输出信号的变化。

3.测量冲激响应。

将函数发生器的输出设置为冲激信号，并观察示波器上输出信号的变化。

记录下输出信号的波形和参数，如幅度、延迟等。

4.测量单位阶跃响应。

将函数发生器的输出设置为单位阶跃信号，并观察示波器上输出信号的变化。

记录下输出信号的波形和参数，如幅度、上升时间等。

5.分析实验结果。

根据测量的波形和参数，进一步分析线性系统的特性。

比较不同输入信号对输出信号的影响，讨论线性系统的时域特性。

4. 实验结果分析根据实验测量的波形和参数，我们可以得出以下结论：1.冲激响应：冲激响应是指系统对一个冲激信号的响应。

通过观察冲激响应的波形，我们可以了解系统的频率响应特性。

例如，当系统为低通滤波器时，冲激响应的幅度在低频时较大，在高频时逐渐减小。

2.单位阶跃响应：单位阶跃响应是指系统对一个单位阶跃信号的响应。

通过观察单位阶跃响应的波形，我们可以了解系统的稳定性和响应速度。

例如，当系统为一阶惯性系统时，单位阶跃响应的上升时间较长，而当系统为二阶系统时，单位阶跃响应的上升时间较短。

5. 实验总结通过本实验，我们深入了解了线性系统时域分析的方法和步骤。

信号与系统 第二章 线性时不变系统的时域分析

r
外加信号 常数A
特解 常数B
r 1i k t i r 1 i 1
tr
sin t或cos t
eλt
k1 cost k2 sin t keλt， λ不是方程的特征根 kteλt， λ是方程的特征根
k t
i 1 i
r 1
r 1i t
e ， λ是方程的r阶特征重根
一、微差分方程的建立以及经典解法
'' 1
di1 (t ) 1 t L i2 ( )d R2i2 (t ) f (t ) dt C
一、微差分方程的建立以及经典解法
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
(1)

t

i ( )d
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
例题，已知线性时不变系统方程如下： y˝(t)+6y΄(t)+8y(t)= f(t), t>0. 初始条件y(0)=1， y΄(0)=2，输入信号f(t)=e-tu(t) , Q求系统的完全响应y(t)。
解：1）求方程的齐次解 特征方程为：m2+6m+8=0 显然特征根为：m1=-2，m2=-4
故原方程的齐次解为：yn(t)= Ae-2t+Be-4t

LTI系统的时域频率复频域分析

2
一、LTI系统时域分析
1. 用单位冲激响应和单位脉冲响应表示LTI系统
x ( t ) h ( t ) y(t)x(t)h(t)
x[n] h[n]
y[n]x[n]h[n]
3
2. 用微分和差分方程描述的因果LTI系统
一个LTI系统的数学模型可以用线性常系数微分方程或线性常 系数差分方程来描述。分析这类系统，就是要求解线性常系数 微分方程或差分方程。 对于因果系统，当输入为0时，输出也为0。也就是说对于因 果LTI系统，其输出的初始状态为零，此时的输出常称为系统 的零状态响应。 系统分析时，往往不是通过微分/差分方程的时域求解，而是 通过频域或复频域分析来求解方程。但是对离散LTI系统，其 差分方程的时域递归解法在数字滤波器的设计中有非常重要的 应用。
4
4 4
4
4 4
依此 ,可 y [n 类 ]得 1 n 1 推 ,n 1 . 或者 y [n ] 1 写 n 1 u [n 成 1 ]
4
4
8
3. LTI系统的方框图表示
（1） 离散时间系统
一阶差分方程 : y [n ] a[n y 1 ]b[n x ]
2. 根据系统的描述，求出 H ( j )
3. Y (j)X (j)H (j)
4. y(t)F1[Y(j)]
16
从信号分解观点分析
若 x ( t) ： e j t
则 y ( t) ： h ( t) x ( t) h () e j ( t ) d h () e jd e j t H (j) e j t
x[n][n1] 1,n1,
对于因果y系 [n]统 0,n必 1. 有
0,n1

信号与系统matlab实验线性时不变系统的时域分析(最新整理)


答案
1. x n hn u n u n 4 ;
nx=0:9;x=ones(1,length(nx)); nh=0:4;h=ones(1,length(nh)); y=conv(x,h); % 下限=下限1+下限2 ny_min=min(nx)+min(nh); % 上限=上限1+上限2 ny_max=max(nx)+max(nh); ny=ny_min:ny_max; subplot(3,1,1);stem(nx,x); xlabel('n');ylabel('x(n)');axis([ny_min ny_max 0 max(x)]); subplot(3,1,2);stem(nh,h); xlabel('n');ylabel('h(n)');axis([ny_min ny_max 0 max(h)]); subplot(3,1,3);stem(ny,y); xlabel('n');ylabel('x(n)*h(n)');axis([ny_min ny_max 0 max(y)]);
到连续卷积的数值近似，具体算法如下：
y=conv(x,h)*dt
% dt 为近似矩形脉冲的宽度即抽样间隔
例 2-2：采用不同的抽样间隔 值，用分段常数函数近似 x t u t u t 1 与
h t sin t u t u t π 的 卷 积 ， 并 与 卷 积 的 解 析 表 达 式
x(t)
h(t)
1 0.5
0 0 0.5 1 1.5 2 2.5 3 3.5 t
1 0.5
0 0 0.5 1 1.5 2 2.5 3 3.5 t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（1）差分方程 离散系统的基本部件有移位器（ 离散系统的基本部件有移位器（也叫做延时器 或延迟器）、相加器和倍乘器，这些基本部件 或延迟器）、相加器和倍乘器， ）、相加器和倍乘器 常用以下框图来表示： 常用以下框图来表示：
下图是一个简单的离散系统，它由一个延时器、 下图是一个简单的离散系统，它由一个延时器、 是一个简单的离散系统 一个相加器和一个倍乘器组成。 一个相加器和一个倍乘器组成。根据图中各个 部件的连接关系和各个部件的基本功能， 部件的连接关系和各个部件的基本功能，写出 该系统输入 x[n] 和输出 y[n] 之间的关系为： 之间的关系为：
重要意义： （1）零状态响应能够真实地反映系统特性； （2）系统的零状态响应可以用卷积的方法 求解。
2．零输入响应和零状态响应的求解 ．
零输入响应的求解 零输入响应的解的形式应和微分方程齐次解的 形式相同，它应是微分方程齐次解中的一部分。 如果一个 N 阶微分方程的 N 个特征根 αi 都是单 根，则零输入响应 yzi(t) 可写为：
例1-17－例1-20
2.时不变性 时不变性
时不变性的含义是，如果系统的输入在 时间上有一个平移 t0，则由其引起的响 应也产生一个同样的平移.
例1-14－例1-16
3.因果性 因果性
如果一个系统在任何时刻的输出只与系 统当前时刻的输入和过去的输入有关， 而与系统未来的输入无关，则这个系统 就是因果系统。 例1-12
1.冲激响应的特点 冲激响应的特点
y zi (t ) =
N
∑
i =1
Ci e α i t
待定系数 Ci 完全由系统的起始状态 y(k)(0-) 确定
零状态响应的求解 齐次解中剩下的一部分将和特解一起组 成系统的零状态响应 。 零状态响应有3种求解方法 （1）零状态响应＝完全响应－零输入响应； （2）利用系统从起始状态 y(k)(0-) 到初始 状态 y(k)(0+) 的跳变量y(k)(0) 来求解系 统的零状态响应 ； （3）卷积法
第二章 线性时不变系统的时域分析
学习目标： 学习目标： (1) 正确理解零输入响应、零状态响应、冲激 正确理解零输入响应、零状态响应、 响应和阶跃响应的基本概念； 响应和阶跃响应的基本概念； (2)能应用不同的方法求解零状态响应和冲激 能应用不同的方法求解零状态响应和冲激 响应； 响应； (3)掌握用冲激响应卷积求解零状态响应的原 掌握用冲激响应卷积求解零状态响应的原 理和方法 (4) 掌握用冲激响应表征系统的基本特性。 掌握用冲激响应表征系统的基本特性。
框图法就是用一个方框来表示一个系统 或子系统，而方框中的符号表示输入和 输出之间的关系 :
系统分类
线性系统和非线性系统 时不变系统和时变系统 因果系统和非因果系统 稳定系统和不稳定系统 我们主要讨论线性时不变系统。 我们主要讨论线性时不变系统。
二、系统的基本性质
系统的基本特性包括有线性、时不变性、 因果性和稳定性等 。 1.线性 1.线性 如果系统的输入和输出之间满足叠加性 和比例性，则该系统就是线性系统。 叠加性 比例性 线性系统
n
∑C e
k k =1
αkt
⑵ 如果在特征根中， 是 k 重特征根 am ， 则与 am 相对应的齐次解为:
k
∑C t
i i =1
k i
e
ai t
=0
⑶ 如果特征根中有共轭复根 α ± jβ ，则 共轭复根所对应的齐次解为:
e (C1 cos β t + C 2 sin β t )
αt
在上述三种齐次解中，Ci 是待定系数， 它的确定与特解有关。 举例2.14
一、系统的定义及表示
系统：具有特定功能的总体， 系统：具有特定功能的总体，可以看作信号 的变换器、处理器。 的变换器、处理器。 系统模型：系统物理特性的数学抽象。 系统模型：系统物理特性的数学抽象。 系统的表示方法 （1）数学表达式：系统物理特性的数学抽象。 ）数学表达式：系统物理特性的数学抽象。 （2）系统框图：形象地表示其功能。 ）系统框图：形象地表示其功能。
在特征根都是单根的情况下，零状态响 应的形式为：
y zs (t ) =
N
∑
i =1
Ai eαit + B(t )
零输入响应和零状态响应的概念同样适 用于离散系统，而且，它们的求解方法 也相同。
dy(t ) + 3 y (t ) = 3u (t ) 举例：已知 dt
y(0-)=3/2，求自由响应、强迫响应、零
如果系统的起始状态y(0－)≠0，则系统的 输出 y(t) 和系统的输入 x(t) 之间就不满 足线性和时不变性。然而，只要 y(0－)=0， y(t) 和 x(t) 之间就能够满足 线性和时不变的关系。
完全响应等于零输入响应加上零状态响 应：
零输入响应：在激励信号 x(t) 为0，或者 不考虑激励信号的作用时，由系统起始 状态 y(k)(0-) 产生的响应； 零状态响应：当系统起始状态 y(k)(0-) 为 0，或者不考虑系统的起始状态时，由激 励信号 x(t) 产生的响应。
y(t)与y[n]计算结果的比较
四、零输入响应和零状态响应
1．起始状态对系统的影响 ． 用线性方程 y ( t ) = a x ( t ) + b 来描 述的系统可能不是一个线性系统！为什 么？ 如果方程中没有常数项 b ，则 y(t)=ax(t) 所描述的系统就是一个线性系统 。
将系统的响应分为两部分： （1）与激励信号无关，完全由某些“常数” 决定； （2）完全由激励信号确定。 结论：完全由激励信号确定的响应与激励 信号之间就可能满足线性关系了。 举例说明
常见激励信号的特解形式
微分方程的特解与激励信号有关，根据 不同的激励信号，特解也有不同的形式。 几种常见的激励信号，特解的形式见表 2.1所示。 特解的求解过程一般是将表2.1中和激励 信号相对应、并具有待定系数 B 的特解 代入微分方程后求出待定系数 B，这样 也就求出了特解。
微分方程的齐次解和特解求出以后， 微分方程的齐次解和特解求出以后 ， 其完全解的 形式也就确定下来了。 但是， 形式也就确定下来了 。 但是 ， 完全解中的待定系 数则需要由方程给定的初值来确定。 数则需要由方程给定的初值来确定。 为求得这些初值， 为求得这些初值 ， 我们将系统在激励信号加入前 瞬间的状态定义为系统的起始状态， 瞬间的状态定义为系统的起始状态，记为 y(k)(0-)； ； 而将系统在激励信号加入后瞬间的状态定义为系 统的初始状态， 记为y 统的初始状态 ， 记为 (k)(0+) ， 确定系统完全响应 所需要的初值是初始状态 y(k)(0+)， （ 系统的初始 ， 时刻的响应） 状态就是系统在 t=0+ 时刻的响应）。
这个常系数线性微分方程， 这个常系数线性微分方程，其完全解由 齐次解和特解两部分组成 。 齐次解是微分方程在输入为0时的齐次 齐次解是微分方程在输入为 时的齐次 方程的解（ 方程的解（式2.111） ） 而特解则是在输入的作用下满足微分方 程式(2.109) 的解。 的解。 程式
对于式(2.109)的微分方程，相应的齐次 方程为
1.连续时间 连续时间LTI系统的微分方程及其求解 连续时间 系统的微分方程及其求解 对连续时间LTI系统，如果 x(t) 为输入， y(t) 为输出，则描述输入和输出之间的 微分方程为：
∑
d y (t ) ak = k dt k =0
N
k
∑
d x(t ) bk dt k k =0
N
k
(2.109)
求解差分方程的方法有两种： （1）迭代法，也叫做递归法，这种方法易 于用计算机求解，但不易给出一个闭式 的解答。 （2）经典法，这种方法完全可以按照微 分方程的求解方式进行，其完全解也分 为齐次解和特解两部分。 例2.15
根据特征根的性质， 根据特征根的性质，差分方程的齐次解也 有以下三种形式： 有以下三种形式： ⑴ 如果特征根 α1、α2 、αn 都是单根， 则齐次解的形式为 ⑵ 如果在特征根中， αm 是 K 重特征根， 则齐次解中与 αm 相对应的有 K 项，其 形式为
数学表达式： 数学表达式：微分方程和差分方程
常用的系统描述方法是数学方程，包括 有用于连续系统的微分方程和用于离散 系统的从差分方程。 列写系统的数学方程有两条基本依据： （1）系统内部元器件或子系统的连接关系 （拓扑约束）； （2）另一条是元器件或子系统的电气特性 （性能约束）。
系统的框图表示法
y[n] ay[n 1] = x[n]
一阶差分方程
N 阶离散系统的差分方程为： 阶离散系统的差分方程为：
∑ a y[n k ] = ∑ b x[n k ]
k k k =0 k =0
N
M
(2.113)
离散系统差分方程的形式类似于连续系统的微分方 程，只不过这里用差分信号替代了微分方程中的微 分信号而已。 分信号而已。 （2）差分方程的求解 ） 对于一阶差分方程式， 对于一阶差分方程式，如果输入信号 x[n]=δ[n] ， 将如何求得呢？ 则输出信号 y[n] 将如何求得呢？
输入响应、零状态响应和完全响应。
解： 自由响应：1/2e-3t 强迫响应 ：1 3 3 t 零输入响应：y zi (t ) = e
2
y zs (t ) = 1 e 3t 零状态响应：
1 3 t y 完全响应 ： (t ) = e + 1 2
t >0
t >0
五、单位冲激响应
单位冲激响应也简称为冲激响应，常用 符号 h ( t ) 或 h [ n ] 表示 。 单位冲激响应是系统在单位冲激信号激 励下的零状态响应； 或者说，是系统在零状态的条件下对单 位冲激信号激励时的响应。
⑶ 如果特征根中有共轭复 根 α ± jβ ，则共轭复根所 对应的齐次解为