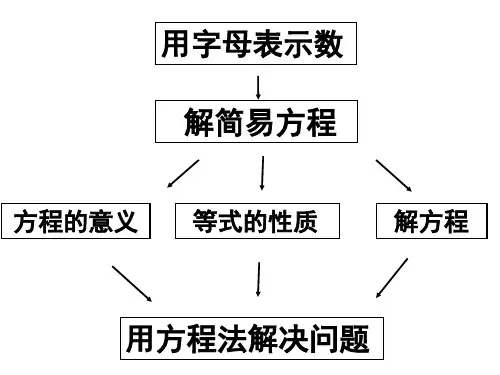
用字母表示数和简易方程复习

第五单元简易方程一、知识梳理1.用字母表示数。

（1）用字母表示数。

①字母与数字相乘，可以省略乘号，数字要写在字母的前面。

如x×6＝6x；如果1与字母相乘，可以省略1与乘号，如m×1＝m。

②字母与字母相乘，字母中间的乘号可以记作“•”，也可以省略不写。

③含有加减关系的代数式，后面有单位时，代数式必须用括号括起来。

如（3a－2b）米，而5n米就不用加括号了。

④a2与2a的区别：a2表示2个a相乘，是a×a；2a表示2个a相加，是a＋a。

（2）用字母表示运算定律。

加法交换律：a＋b＝b＋a；加法结合律：（a＋b）＋c＝a＋（b＋c）；乘法交换律：ab＝ba；乘法结合律：（ab）c＝a（bc）；乘法分配律：（a＋b）c＝ac＋bc。

(3)用字母表示计算公式。

长方形的面积公式：s＝ab；长方形的周长公式：c＝2（a＋b）；正方形的面积公式：s＝a2；正方形的周长公式：c＝4a。

（4）用字母表示常见的数量关系。

如路程、速度和时间之间的关系可以表示为s＝vt。

（5）求含有字母的式子的值。

用含有字母的式子表示指定的数量，再把字母的取值代入式子中求值。

（6）字母的取值范围。

在含有字母的式子里，字母的取值范围是由实际情况决定的。

2.方程的意义。

（1）方程的意义。

含有未知数．．就是方程。

．．．的等式（2）等式的性质。

等式的性质1：等式两边加上或减去同一个数，左右两边仍然相等。

等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，左右两边仍然相等。

3.解方程。

（1）方程的解与解方程。

使方程左右两边相等的未知数的值，叫做方程的解；求方程的解的过程叫做解方程。

（2）解形如x±a＝b、ax＝b、ax±b＝c和a（x±b）＝c的方程。

依据等式的性质来解此类方程。

（3）检验。

把求得的未知数的值代入原方程，看方程左边的值是否等于右边的值。

如果相等，所求的未知数的值就是原方程的解，否则就不是。

简易方程单元复习学生姓名年级学科授课教师日期时段核心内容用字母表示数、解简易方程及其应用课型一对一/一对N教学目标1、会用字母表示数、运算定律、公式、数量关系；2、会解方程，会列方程解决实际问题。

重、难点重点：会用字母表示数量关系，掌握方程有关概念，会列方程解决实际问题；难点：找出题中等量关系列方程解决实际问题。

课首沟通1、上讲回顾（错题整理）；2、作业检查及指导讲评；3、询问学习进度和知识掌握情况等。

知识导图课首小测1.填空。

（1）工地上有a吨水泥，每天用去2吨，用了b天后，还剩下（）吨。

（2）小明今年a岁，爸爸今年30岁，爸爸比小明大（）岁，十年后爸爸比小明大（）岁。

（3）一个两位数，十位数上的数字是a，个位上的数字是b，这个数是（）。

（4）x减去2与4的积，差是5，x是多少？列方程为（）（5）9与0.8的积减去一个数的2倍，差是1.2，设这个数为x，这个数是多少？列方程为（）2.[单选题] 下面的式子中是方程的是（）。

A． B. C. D.3.[单选题] 如果，那么（）。

A．25 B.7 C.31 D. 494.[单选题] 甲数是，比乙数的3倍少b，乙数用式子表示是（）。

A． B. C. D.5.方程是等式，但等式不一定是方程。

（）6.a×b的值一定大于a+b的值。

（）7.解方程。

知识梳理导学一：用字母表示数知识点讲解 1例 1. 填空。

我爱展示1. 用字母表示数。

（1）比x的2倍少3的数。

（2）一列火车每小时行78千米，t小时行多少千米？（3）李庄m公顷的麦田，共收a千克的小麦，平均每公顷产小麦多少千克？（4）a与b的差除以4的商。

（5）办公桌每张单价a元，办公椅每把单价b元，买m套办公桌椅共付多少元？导学二：解简易方程知识点讲解 1例 1. 根据图意列出方程。

例 2. 解下列方程。

例 3. 解下列稍复杂方程。

我爱展示1. 解下列方程。

导学三：实际问题与方程知识点讲解 1例 1. 学校买来10箱粉笔，用去250盒后，还剩下550盒，平均每箱多少盒？例 2. 食堂运来150千克大米，比运来的面粉的3倍少30千克。

《简易方程》的整理与复习教学目标：1、帮助学生整理式与方程的知识体系，学会用字母表示数，体会用字母表示的简洁性。

2、正确理解方程的意义，会熟练地解一些简易方程，能自觉进行检验。

初步沟通算式、代数式、具体数量之间的关系。

3、进一步理解基本的数量关系，会根据实际情况选用方程解决问题，培养学生的合作学生能力，提高学生的方程及代数意识。

教学重点：明确字母表示数的意义和作用；会灵活的用方程解答两步简单的实际问题。

教学难点：找等量关系式，用方程解决实际问题。

教学过程：一、导入师：回忆一下，我们在简易方程这个单元学习了哪些的知识呢？用字母表示数；认识方程，解方程；用方程解决实际问题。

师：今天，我们就围绕这三方面进行整理和复习。

二、进入复习1、用字母表示数（1）师：大家先想想，我们用字母表示过些什么呢？请跟小组同学说一说吧！（生讨论）用字母表示数量关系；用字母表示计算公式，比如：梯形的面积计算公式S=(a+b)×h÷2。

师：同学们，字母还可以表示什么计算公式呢？运算定律。

师：看来，同学们对用字母表示运算定律掌握得还真不错，下面老师来写个式子，你们瞧瞧：b/a×d/c=b×d/a×c,大家想想，这个式子表示什么呢？（分数乘法的计算方法）看来，我们还可以用字母来表示计算方法。

（板书）大家说说在简写时我们要注意什么呢？生：当字母乘字母或数字乘字母时，乘号可以省略不写或改写成“·”。

当乘号省略不写时，数字应写在字母的前面。

师：同学们，看来你们对这块知识掌握得不错，小精灵明明想考考你们，怎么样，我们来看看。

（2）完成补充题。

师：咱们一起来观察一下左边，（手指着）你发现用字母来表示来这些式子有什么好处呢？（好记、更加简洁、表示未知量。

）2、复习方程。

师:下面我们来复习一下有关方程的知识,先想想什么叫方程?1）判断下面哪些式子是方程？2）等式和方程有什么联系和区别？用怎样集合圈表示？3）师：同学们，你会解这些方程吗？师：同学们，刚才我们在解方程的原理是什么呢？（等式的性质）师：解方程要注意什么？3、列方程解决问题（1）一个梯形的面积是265平方米，上底是20米，下底是33米，高是多少米？师：请同学们轻声读一读这道题。

第5讲 简易方程用字母表示数量关系用字母表示运算定律和计算公式用字母表示数借助字母解决实际问题并代入求值方程的意义解方程解简易方程实际问题与方程解不同类的方程解方程等式的性质方程和等式(1)等式的意义：表示等号两边是相等关系的式子叫等式。

(2)方程的意义：含有未知数的等式叫方程。

(3)方程与等式的关系：等式的范围比方程的范围大。

方程都是等式，但等式不一定是方程。

方程的意义使方程左右两边相等的未知数的值，叫做方程的解。

方程的解实际上是一个数。

求方程的解的过程叫做解方程。

解方程实际上是一个过程。

知识点一：用字母表示数1. 用字母表示数量关系（1）可以用字母或含有字母的式子来表示一个数或表示数量关系；（2）字母与数字相乘时，把乘号省略。

省略乘号时，一般把数字写在字母前面。

含有字母的式子中的加、减、除号不能省略。

2. 用字母表示运算定律和计算公式（1）在含有字母的式子里，只有字母与字母、数字与字母之间的“×”才能简写成“.”或者省略不写。

注意：省略乘号后，数字必须写在字母的前边。

（2）应用公式求值解决问题的步骤：第一步：写出字母公式第二步：把字母表示的数值代入公式第三步：计算出结果，记住写单位3. 用字母表示复杂的数量关系（1）不同的式子可以表示相同的数量关系。

（2）将字母的具体数值代入含有字母的式子中,即可求得相应式子的值。

4. 化简含有字母的式子并代入数据求值计算含有字母的式子的时候，可以先运用运算定律将含有字母的式子进行化简,再求值。

知识点二：解简易方程1.方程的意义（1）方程的意义：含有未知数的等式是方程。

（2）方程必须具备的两个条件：一是等式；二含有未知数。

2.方程一定是等式；但等式不一定是方程。

3. 所有的方程都是等式，但等式不一定都是方程。

4.等式的性质等式的性质1：等式两边加上或减去同一个数，左右两边仍然相等。

等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。

用字母表示数简易方程1、正方形（C：周长 S：面积 a：边长）周长＝边长×4 C=4a面积=边长×边长S=a×a2、正方体（V:体积 a:棱长）表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形（ C：周长 S：面积 a：边长）周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4、长方体（V:体积 s:面积 a:长 b: 宽 h:高）(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高 V=abh某宾馆大厅有4根同样的长方体水泥柱，每根高4.4米，底面和上面都是正方形，边长0.8米。

①每根柱子一周有多长？②4根柱子的表面积为多少平方米？③如果在这4跟柱子上包上壁纸（壁纸5元/平方米），至少要花多少钱?④这4根柱子的体积是多少立方米？学校音乐室铺了2000块长60厘米、宽10厘米、厚2厘米的地转，这个教室面积是多少平方米?一间教室长9米,宽6米,高3.6米。

要粉刷这间教室的屋顶和四壁,除去门窗和黑板面积15平方米,需要粉刷的面积是多少平方米?5、三角形（s：面积 a：底 h：高）面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高一只蚂蚁沿着屋顶侧面爬了一圈（屋顶如右图所示），此屋顶侧面是由两个完全一样的直角三角形组成的。

①蚂蚁爬了多长？②这个屋顶侧面的面积是多少？6、平行四边形（s：面积 a：底 h：高）面积=底×高 s=ah7、梯形（s：面积 a：上底 b：下底 h：高）面积=(上底+下底)×高÷2 s=(a+b)× h÷2如右图所示：A-B-C-D-A为等腰梯形，线段AE平行于线段BC，AB=5m,BC=5m,BD=4.5m,CF=10m。