当前位置：文档之家 › chap4-晶体的宏观对称.ppt

chap4-晶体的宏观对称.ppt

  • 格式：ppt
  • 大小：12.29 MB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

晶体的宏观对称 点群 对称型 ppt课件

晶体的宏观对称 点群 对称型 ppt课件
第二章 晶体的宏观对称
对称的概念
晶体对称的特点
对称要素和对称操作
晶体的对称定律
对称要素的组合
点群和对称型的概念及其推导
晶体的分类
对称型的国际符号和圣佛利斯符
号 2020/10/15
1
晶体学
2.5 对称要素的组合
任意两个对称要素同时存在一个晶体上时，将 产生新的对称要素，且产生的个数一定。
例：四方四面体
Li42L2 2P
2020/10/15
黄铜矿
Li4+
L2⊥(或P//)
=
Li4
10
2L22P
晶体学
五、32个对称型及其推导
晶体形态中，全部对称要素的组合，称为该晶 体形态的对称型或点群。一般来说，当强调对称 要素时称对称型，强调对称操作时称点群。
为什么叫点群？因为对称型中所有对称操作可构 成一个群，符合数学中群的概念，并且在操作时 有一点不动，所以称为点群。
晶体学
对称要素的组合
2020/10/15
8
晶体学
对称要素组合定理：
定理3：Ln P LnP C （n为偶数） 逆定理： Ln C LnP C （n为偶数）
P C LnP C （n为偶数） 这一定理说明了Ln、P、C三者中任两个可以 产生第三者。
2020/10/15
正长石：
L2+P⊥
=
2020/10/15
14
晶体学
A类对称型（高次轴不多于一个）的推导
6）旋转反伸轴单独存在。可能的对称型为：Li1=C； Li2=P；Li3=L3C；Li4；Li6=L3P。 7）旋转反伸轴Lin与垂直它的L2（或包含它的P）的组 合。根据组合规律，当n为奇数时LinnL2nP，可能的 对称型为：（Li1L2P=L2PC）；Li33L23P=L33L23PC； 当 n 为 偶 数 时 Lin(n/2)L2(n/2)P 可 能 的 对 称 型 为 ： （Li2L2P=L22P）；Li42L22P；Li63L23P=L33L24P。

04宏观对称性精品PPT课件

04宏观对称性精品PPT课件
晶体的宏观对称性
生 物 界 的 对 称 性
4.1 对称性概念
判天地之美,析万物之理。 —— 庄 子
物理学中的对称：物理学定律不随运用时间和地点而改 变，把这样的性质叫对称性。
在所有智慧的追求中，很难找到其他例子能够在深刻的普遍性与 优美简洁性方面与对称性原理相比
——李政道. 对称在科学界开始产生重要的影响始于19世纪.发展到近代，我 们已经知道这个观念是晶体学、分子学、原子学、原子核物理学、 化学、粒子物理学等现代科学的中心观念.
从晶体的数量来看, 大约80%的无机结构和60%的有机 结构具有对称中心.
从晶体学点群来看，32种点群中, 含对称中心的点群有 11种, 而非中心对称点群有21种. 非中心对称点群与对映体 、旋光性、热电效应、铁电效应、压电效应、倍频效应等物 理性质的联系可用下图表示(圈内表示该点群晶体中可能观 察到的某种性质, 圈外表示该点群晶体中不可能观察到的某 种性质）.
旋转反轴 旋转反轴的对称操作是复合
操作：围绕一根直线旋转和对此直线上一点 倒反。
旋转反轴的符号 Ln ，n代表轴次。n可以 为1、2、3、4、6，相应的基转角为360°、 180°、120°、90°、60 ° 旋转反伸轴的作用如下图所示：
1.4.3 对称要素的组合
（1）反映面之间的组合
定理: 如果反映面相交，其交线为旋转轴，基 转角为反映面交角的2倍。
无相当
值
360 °
值
（3）对称中心(C)
对称中心是晶体中心的一个假想点，任意
通过此点的直线的等距离两端，必定找到对应 的点。对称中心的对称操作是对此点的倒反。
晶体中可以没有对称中心，或者有一个对称 中心。
晶体中如果有对称中心，晶体上的晶面必然 都是两两平行（或两两反向平行）且相等。

《晶体的宏观对称性》课件

《晶体的宏观对称性》课件
对称性是晶体学中一个非常重要的概念，它有助于我们理解晶体的结构和性质。
晶体对称性的分类
晶体对称性可以根据其对称操作的不同进行分类，主要包括7种点群和10 种布拉维格子。
点群是指在三维空间中围绕一个点进行对称操作的集合，包括32种不同 的点群。
布拉维格子则是指晶体中原子排列的周期性模式，包括简单格子、复式 格子和面心格子等。
《晶体的宏观对称性》 ppt课件
• 引言 • 晶体的基本概念 • 晶体的宏观对称性 • 晶体对称性的应用 • 晶体的宏观对称性与晶体物理性质的
关系 • 总结与展望
01
引言
课程简介
晶体对称性是晶体学的重要概念 ，它描述了晶体在宏观尺度上的
对称特征。
本课程将介绍晶体对称性的基本 概念、分类和在材料科学中的应
例如，立方晶体具有高度的对称性，因此其光学、电学和热学性质在各个方向 上都是相同的。
对称性破缺与物理性质的变化
对称性破缺的概念
01
当晶体失去原有的对称性时，称为对称性破缺。
对称性破缺对物理性质的影响
02
对称性破缺会导致晶体物理性质的变化，如光学、电学和磁学
性质的各向异性。
对称性破缺的实例分析
03
例如，石墨晶体中的层状结构导致其对称性在垂直于层面的方
在材料科学中的应用
01
晶体对称性与材料性能
材料的物理和化学性质与晶体的对称性密切相关。例如，金属材料的导
电性和导热性、陶瓷材料的硬度等都与其晶体结构对称性有关。
02 03
晶体对称性与材料合成
通过控制材料的晶体对称性，可以合成具有特定性能的新型材料。例如 ，通过改变晶体结构中的原子排列，可以合成具有高强度、高硬度、耐 高温等优异性能的新型陶瓷材料。

《晶体的宏观对称性》PPT课件

《晶体的宏观对称性》PPT课件
• 举例：
（1）蝴蝶的两个相同的部分可以通过垂直平分它的镜面的反映，彼此重合；
（2）花冠通过围绕一根垂直它井通过它中心的直线旋转，可以多次重复其原来 的形象。
2020年11月24日3时55
P10
分
晶体学中的对称 和几何对称概念 是有差别的！
2020年11月24日3时55
P11
分
一、对称（symmetry)概念
P4
毛茛
人为的对称图形
2020年11月24日3时55分
P5
雪花
凡草木花 多五出， 雪花独六 出
2020年11月24日3时55分
P6
雪花为什么是六角形的？
•
古代文献中有许多关于雪花形状的描述
• 早在公元前的西汉时代，《韩诗外传》中就指出：“凡草木花多五出，雪花独六 出。”
•
六出雪花天下奇
• (梅花五瓣，雪花六出）
2020年11月24日3时55
P2
分
一些简单对称图 • 对称的现形象在自然界和我们日常生活中部
很常见。如蝴蝶、花冠等动植物的形体以 及某些用具、器皿，都常呈对称的图形。
对称： 人为对称图形 自然对称图形
2020年11月24日3时55
P3
分
自然界一些对称现象－植物
•
木槿花
2020年11月24日3时55分
P16
分
晶体的对称操作及对称要素
对称操作
对称要素
简单的 反映
平面
对称面
• 北周·庾信《郊行值雪》 :“雪花开六出，冰珠映九光”
• 唐·元稹 “一枝方见秀，六出已同开”
• 唐·高骈“六出飞花入户时”
• 唐·宋之问 “银树长芳六出花”；

晶体化学课件：第四章晶体的宏观对称

晶体化学课件：第四章晶体的宏观对称
Crystallography
11
第四章 晶体的宏观对称
偎回月台泛来走开 林望明映舟客上篷 傍四孤碧渔仙烟一 水山寺泉浦亭花棹 绿观古寒满闲踏远 悠落林井飞伴径溪 悠日幽冷鸥鹤游流
Crystallography
12
第四章 晶体的宏观对称
图形相同部分有规律的重复，称为对称。 对称图形的条件： 有两个或两个以上相同部分； 这些相同部分可以借助于对称动作发生
• 对称元素的符号
– 国际、习惯、图示符号
Crystallography
22
第四章 晶体的宏观对称
对称元素符号
宏观晶体的对称要素
对称要素
对称轴
对称中心
对称面
一次 二次 三次 四次 六次
辅助几何要素
直线
点
平面
对称变换
围绕直线的旋转
对于点的倒反 对于平面的反映
基转角
360˚ 180˚ 120˚ 90˚
习惯符号
L1
L2
L3
L4
国际符号
1234
等效对称要素
图示记号
60˚
L6
C
6
1
L1i
˚ 或C
P
m L2I 双Biblioteka 或粗线倒转轴三次 四次 六次
直线和直线上的定点
绕直线旋转及点的倒
反
120˚ 90˚ 60˚
L3I
L4i
L6i
346
L3+C
L3+P
Crystallography
23
结晶学
第四章 晶体的宏观对称
• 能够使对称物体(或图形)中的各个相同部分 作有规律重复的动作(对称操作)
• some acts that reproduce the motif to create the pattern

crystalchap4_1PPT课件

crystalchap4_1PPT课件
19
一次旋转对称轴 基转角＝360度。 它的书写符号可记为L1或者 1或者 C1 L1 是习惯符号 1 是国际符号 C1 熊夫利斯符号。 一次旋转实际上没有任何操作，因此不做图示表示 图形在旋转一周后与原来的点重复，重复次数为1。 极射赤面投影是空间中任意一点投影点本身。
20
二次旋转对称轴：围绕2次旋转轴转180度可使 晶体结构得到重复，因此基转角＝180度。 它的书写符号记为L2或者2或者C2
10
点对称操作的种类： 反演、反映、旋转、旋转反演
点对称操作的分类： 依据有没有手性的变化进行分类，可分为两类： (a)第一类点对称操作 是真旋转，被作用的对象没有手性的变化，即没 有右手到左手的变化； (b)第二类点对称操作 是像旋转，被作用的对象有手性的变化。
11
二、四种宏观对称要素 (1)旋转对称轴 如果一个物体或图形绕一直线旋转一定角度后，可 使图形的相同部分重合，则称这个物体或图形具有 旋转对称性，相应的直线称为旋转对称轴。
16
晶体对称定律反映了晶体结构 具有空间点阵这个表示原子排 列周期性的潜在的几何图像。
晶体对称定律规定了晶体结构 对称的基本特征，反映了晶体 结构与其它物质体系在对称性 上的区别。
晶体的对称定律不仅被结构分 析实验验证，也为晶体外形面 角测定的资料所证实。
正五边形不能 填满整个空间
17
Fe(C5H5)分子
例如，立方体绕穿过相对面的 面心的轴旋转90度后与原来的 立方体重合. 立方体具有旋转对称性。
12
在旋转过程中，能使图形相等部分重复的最小转 角，称为基转角，用表示。
由于任何图形旋转360度后必能互相重复，因此基 转角必须能整除360度，即360/n=，n为整数
n称为旋转轴的轴次，它表示围绕旋转轴旋转一 周的过程中，图形相同部分重复的次数。

(04)-第4章-宏观对称性

(04)-第4章-宏观对称性

模板中的图片展示页面，您可以根据需要
方法一：更改图片
2. 在图“替换”下拉列表中选择要更改字体。（如下图）
1.选中模版中的图片（有些图片与其他对 ，而不是组合）。
2.单击鼠标右键，选择“更改图片”，选
3. 在“替换为”下拉列表中选择替换字体。 4. 点击“替换”按钮，完成。
PPT放映 设置
PPT放映场合不同，放映的要求也不同，下面将例举几种常用的放映设置方式。 让PPT停止自动播放 1. 单击”幻灯片放映”选项卡，去除“使用计时”选项即可。
晶体的宏观对称性
生 物 界 的 对 称 性
4.1 对称性概念
判天地之美,析万物之理。 —— 庄 子
物理学中的对称：物理学定律不随运用时间和地点而改 变，把这样的性质叫对称性。
在所有智慧的追求中，很难找到其他例子能够在深刻的普遍性与 优美简洁性方面与对称性原理相比
——李政道. 对称在科学界开始产生重要的影响始于19世纪.发展到近代，我 们已经知道这个观念是晶体学、分子学、原子学、原子核物理学、 化学、粒子物理学等现代科学的中心观念.
ห้องสมุดไป่ตู้
穿过正四面体每条棱 并将四面体分为两半 的是一个σd , 共有6个 σd 。
Y
X
从正四面体的每个顶点到对
面的正三角形中点有一条C3 穿过, 所以共有4条C3,可作出 8个C3对称操作。
4.6 32个晶体学点群
晶体的宏观对称操作是点操作，所有宏观对称元素 会通过一个公共交点按一切可能组合起来，产生晶体学 点群. 晶体的宏观对称元素只有8种，晶体点群数目也受 到限制, 只有32种.
旋转反轴 旋转反轴的对称操作是复合
操作：围绕一根直线旋转和对此直线上一点 倒反。

材料物理课件12晶体的宏观对称性

材料物理课件12晶体的宏观对称性

2成. 的Cn。h群因此这这类类群群是包由含Cnn群个与转水动平及反n个映旋面转h反组射合，而
故群共有2n个群元。这类群共有五个。
+
+
6) C1h={h,E}
+
C1h
7) C2h={C2,h,C2h, E}
C2h
++
8) C3h={C3,C3,2h, C3 h, C3 2h, E} 9) C4h={C4,C4=2 C2 ,C4 ,3h ,
C
8
2020/2/24
4
v
d d
2020/2/24
2. 反映面(镜面) (A Plane of Reflection)
h
v
d
d
反映面的阶次
为2，用表示。
d
d
正四面体有9 个反映面 。
2=E
5
3. 对称中心 (Center of Inversion)
与对称中心相应的动作是中心反演(或倒 反)，记作I。
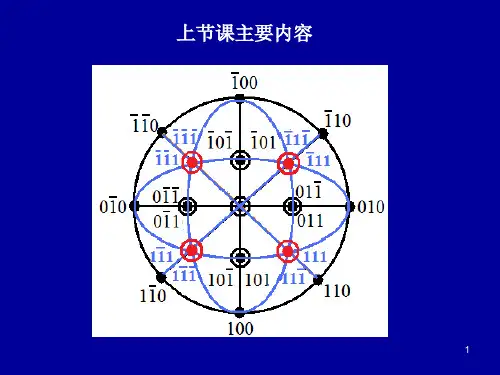
对于立方体群，由於不存在主轴，所以不能用
极射投影图而用单位球来表示，但很繁复。实际
上常直接在立方体中标出各种转轴。
2020/2/24
12
1.3.3 晶体的32类点群
1次. 轴Cn的群转动这操类作群。仅这有种一群个称n次作轴轴，转群动元群都。是绕这n
+
Cn 群是个循环群，即
+
C1
Cn ={Cn,Cn2,…,Cn =n E}
2020/2/24 个反映面穿过此旋转轴。(万花筒定理)
9
1.2.2 对称元素组合原理(Cont’)
三、旋转轴与对称中心的组合 定理：如果在偶次旋转轴上有对称中心，那么 必有一反映面与旋转轴垂直相交于对称中心。 推论：在有对称中心时，图形中偶次轴数目
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• Motif：the fundamental part of a symmetric design that, when repeated, creates the whole pattern
晶体学
对称要素
• 对称要素(symmetry element)：在进行对称操作 时所凭借的辅助几何要素——点、线、面等。
6
= the symbol for a twofold rotation
晶体学
对称轴(Ln)之对称操作
• 对称轴
二次(two-fold rotation)
A Symmetrical Pattern
– 变换矩阵
cos sin 0
sin cos 0
0
0 1
6
第二步
第一步
6
晶体学
对称轴(Ln) 对称操作之平面图解
•(没有5-fold 和 > 6-fold 的)
6
6
6
6
6
6
6
6
1-fold
2-fold
3-fold
4-fold
6-fold
变换矩阵： cos sin 0 sin cos 0
0
0 1
晶体学
晶体的对称定律：
由于晶体是具有格子构造的固体物质，这种质点格 子状的分布特点决定了晶体中只能出现轴次(n)为一次、 二次、三次、四次和六次的对称轴，而不可能存在五次 及高于六次的对称轴。
对称面
平面 对于平面的反映
P m L2i 双线或粗线
旋转反伸轴
三次 四次 六次
直线和直线上的定点
绕直线旋转及点的反
伸
120˚ 90˚ 60˚
L3i
L4i
L6i
3
4
6
L3+C
L3+P
晶体外形可能存在的对称要素和相应的对称 操作如下：
晶体学
对称面
对称面—P 操作为反映。可以有多个对称面存在，如3P、
6P等。
(请同学们在晶体模型上找对称轴)
晶体学
对称轴(Ln)之对称操作
• 对称轴
二次(two-fold rotation)
A Symmetrical Pattern
– = 360o/2 rotation – to reproduce a
6
motif in a
symmetrical
pattern
6
晶体学
变换矩阵
( m包含x、y轴)
x x y y
m
z z
1 0 0
0 1 0
0 0 1
m包含x、z轴 ? m包含y、z轴 ?
m在其他位置 ?
晶体学
对称轴
☆对称轴—Ln 操作为旋转。其中n 代表轴次，意指旋转 360度相同部分重复的次数。旋转一次的角度为基转角
，关系为：n=360/ 。
第四章 晶体的宏观对称
对称的概念 晶体对称的特点 对称要素和对称操作 对称要素的组合 对称型及其推导 晶体的对称分类 准晶体的分类
晶体学
一、对称的概念
Symmetry
• 是宇宙间的普遍现象 • 是自然科学最普遍和最
基本的概念 • 是建造大自然的密码 • 是永恒的审美要素
晶体学
对称的概念
• 物体(或图形)中相同 部分之间有规律的重复。
晶体学
二、晶体对称的特点
由于晶体内部都具有格子构造，通过平移，可使相同 质点重复，因此，所有的晶体结构都是对称的。
晶体的对称受格子构造规律的限制，因此，晶体的对 称是有限的，它遵循“晶体对称定律” 。
晶体的对称不仅体现在外形上，同时也体现在物理性 质上。
对称操作 ＝ 对应点的坐标变换
(x, y, z)
(X, Y, Z)
X a11x a12 y a13 z Y a21x a22 y a23 z Z a31x a32 y a33 z
or
X x Y y Z z
对称变换矩阵
a11 a12 a13 a21 a22 a23
(请同学们在晶体面图解
• 对称面(mirror)
– Reflection across
m
a “mirror plane”
reproduces a
motif
= symbol for a mirror
晶体学
对称面(m)之对称操作
• 对称面(mirror)
a31 a32 a33
晶体学
对称要素符号
宏观晶体的对称要素
对称要素
辅助几何要素 对称操作
一次
对称轴 二次 三次 四次
直线 围绕直线的旋转
六次
对称中心
点 对于点的反伸
基转角 习惯符号 国际符号
360˚ 180˚ 120˚ 90˚ 60˚
L1
L2
L3
L4
L6
1
2
3
4
6
等效对称要素 图示记号
C
ī
L1i ˚ 或C
• 对称要素种类
– 对称中心(center of symmetry) – 对称面(symmetry plane) – 对称轴(symmetry axis) – 旋转反伸轴(rotoinversion axis) – 旋转反映轴(rotoreflection axis)
• 对称要素的符号
晶体学
对称要素之对称操作
对称轴(Ln)之对称操作
• 对称轴
Operation
二次(two-fold rotation)
A Symmetrical Pattern
– = 360o/2 rotation
– to reproduce a motif in a symmetrical pattern
6 Motif
Element
6
= the symbol for a twofold rotation
为什么呢？
1、直观形象的理解：
垂直五次及高于六次的 对称轴的平面结构不能 构成面网，且不能毫无 间隙地铺满整个空间, 即不能成为晶体结构。
晶体学
对称轴(Ln)之对称操作
• 对称轴
二次(two-fold rotation)
A Symmetrical Pattern
– = 360o/2 rotation
– to reproduce a motif in a symmetrical pattern
第二步
6 Motif 第一步 Element
因此，由以上可见：格子构造使得所有晶体都是对称 的，格子构造也使得并不是所有对称都能在晶体中出现 的。
晶体学
三、晶体的宏观对称 要素和对称操作
对称操作(symmetry operation)
• 能够使对称物体(或图形)中的等同部分作有 规律的变换动作(对称操作)
• some acts that reproduce the motif to create the pattern