晶体宏观对称性

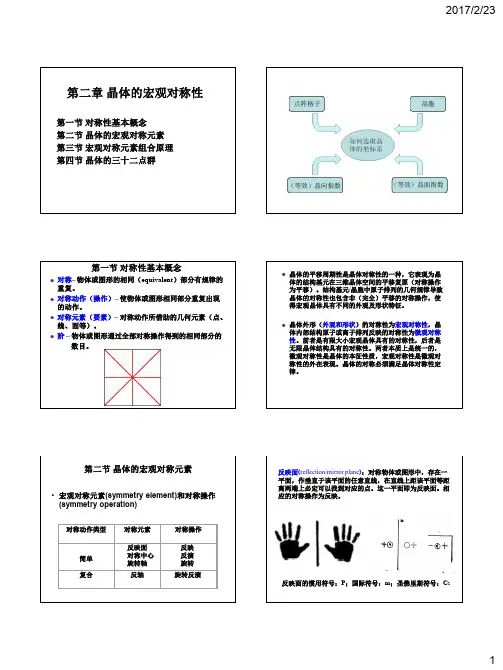
第三章晶体的宏观对称性第一节对称性基本概念第二节晶体的宏观对称元素第三节宏观对称元素组合原理第四节晶体的三十二点群第一节对称性基本概念z对称–物体或图形的相同部分有规律的重复。

z对称动作（操作）–使物体或图形相同部分重复出现的动作。

z对称元素（要素）--对称动作所借助的几何元素（点、线、面）。

z晶体外形的对称为宏观对称性，晶体内部结构原子或离子排列的对称性为微观对称性。

前者是有限大小宏观物体具有的对称性，后者是无限晶体结构具有的对称性。

两者本质上是统一的。

宏观对称性是微观对称性的外在表现。

晶体的对称必须满足晶体对称性定律。

晶体对称性对称自身：国际符号为1，习惯记号为L1。

当它处于任意坐标中的坐标原点时，它的坐标是1(000)，所导出的一般位置等效点系为：x,y,z→x,y,z (1(000))反映面（reflection plane ）：对称物体或图形中，存在一平面，作垂直于该平面的任意直线，在直线上距该平面等距离两端上必定可以找到对应的点。

这一平面即为反映面。

相应的对称操作为反映。

反映面的惯用符号：P ；国际符号：m ；圣佛里斯符号：Cs反映面的极射赤面投影对称中心（inversion center)：对称物体或图形中，存在一定点，作通过该点的任意直线，在直线上距该点等距离两端，可以找到对应点，则该定点即为对称中心。

相应的对称操作为反演。

对称中心的惯用符号：C；国际符号：1；圣佛里斯符号：C对称中心的极射赤面投影返回旋转轴（rotation axe）：物体或图形中存在一直线，当图形围绕它旋转一定角度后，可使图形相同部分复原，此直线即为旋转轴。

相应的对称操作为旋转。

在旋转过程中，能使图形相同部分复原的最小旋转角称为该对称轴的基转角（α）。

任何图形在旋转一周（360o）必然自相重复，因此有：360/ α= n n正整数n表示图形围绕旋转轴旋转一周过程中，图形相同部分重复的次数，因此n定义为旋转轴的轴次。

第四章晶体的宏观对称在第二章中已经介绍，晶体的生长过程，实质上就是质点按照空间格子规律有规则地进行堆积的过程；所以，只要生长时有足够的自由空间，晶体就必然会长成一定形状的几何多面体。

例如石盐常成立方体，而α-石英经常长成带有尖顶的六方柱体，等等。

在具有几何多面体外形的晶体——结晶多面体上，最突出的一个性质就是它的对称性。

晶体外形上的对称性是由其内部格子构造的对称性所决定的。

所以，一切晶体都是对称的。

不过，不同晶体之间的对称性往往又是有差别的，这表现在它们的对称要素可以有所不同，并且因此构成不同的对称型。

所以，有必要同时也有可能，根据晶体的对称特点来对晶体进行分类，即划分出不同的晶族和晶系。

由于晶体的对称性从本质上来讲取决于其内部的格子构造，因此，晶体的对称性不仅包含几何意义上的对称，而且也包含物理意义上的对称，亦即晶体中凡是具有方向性的物理性质，例如折射率、电导率、弹性模量、硬度等等，它们也都呈现相应的对称关系。

这是因为，晶体的各项物理性质都是取决于其组成质点的种类和它们的排列方式的。

所以，晶体的对称性决定并影响着晶体中涉及到几何及物理两方面的一切性质。

反过来，根据晶体的几何外形以及它们的一系列物理性质，又可以用来正确地确定晶体的对称性。

所以晶体的对称性对于我们认识晶质矿物的一系列特性都具有重要的意义。

另一方面，晶体的对称性对于晶体的利用还具有指导意义。

在本章中我们将依次阐述以上的有关内容，但限于讨论晶体外形上的对称，即晶体的宏观对称。

第一节对称的概念和晶体对称的特点一、对称的概念图形相同部分有规律的重复，称为对称。

具有对称特征的图形，称为对称图形。

对称是自然科学中最普遍的一种基本概念。

自然界许多东西都具有对称特点，如植物枝叶的对生与互生，花瓣、动物形体及器官的对称生长、晶体界限要素的对称分布等；建筑物、交通工具、生活用品等，常具有对称的外形；在装饰、装潢设计、纺织品中也常可见到对称图案。

所有对称物体和对称图案统称为对称图形。

晶体的宏观对称性物理科学学院 季淑英 2014020231摘 要: 晶体是内部原子或离子在三维空间呈周期性重复排列的固体，通过对晶体三类宏观对称操作的介绍，找出了晶体的8种基本宏观对称操作。

关键词：对称中心； 反映面； 旋转轴一 什么是晶体人们最早认识晶体是从石英开始的，只知道它天然的具有规则的几何多面体，真正揭开晶体内部结构是在1914年，人类首次测定了Nacl 的晶体结构。

此后，人们积累大量测定资料开始认识到：无论晶体的外形是否规则，它们内部的原子有规则地在三维空间呈周期性重复排列。

所以，晶体是内部原子或离子在三维空间呈周期性重复排列的固体，或着说晶体是具有格子结构的固体。

而晶体的规则几何外形，只是晶体内部格子构造的外在部表现。

二 晶体的宏观对称对称性是晶体的基本性质之一，一切晶体都是对称的；但不同的晶体的对称性往往又是互有差异的。

1 对称操作对一种晶体而言,其内部结构的质点表现出某种对称性的规律排列,当在进行某种操作（线性变换）后能使自身复原,这种对称性是晶体的一个客观存在的基本性质,是晶体内部结构的规律在几何形状上的表现,晶体的许多宏观性质都与其结构上的对称性有密切关系。

对称操作：维持整个物体不变而进行的操作称作对称操作，物体在某一正交变换下保持不变，即：操作前后物体任意两点间的距离保持不变的操作。

一个物体的对称操作越多，其对称性越高。

例如密度ρ作为位矢r 的函数，即）r （ρ。

我们可以定义一个引起坐标变换的操作g 满足’r gr r =→，如果这导致）r （）gr （）’r （ρρρ==那么g 是）r （ρ的一个对称操作。

2 对称元素对称操作过程中保持不变的几何要素：对称点，反演中心（i ）；对称线，旋转轴（n 或者n C ）和旋转反演轴（n ）；对称面，反映面（m ）等。

以上，考察在一定几何变换之下物体的不变性，使用的几何变换（旋转和反射）都是正交变换——保持两点距离不变的变换：⎪⎪⎪⎭⎫ ⎝⎛•⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛z y x a a aa a a a a a z y x 333231232221131211，，，其中，M 为正交矩阵，⎪⎪⎪⎭⎫⎝⎛=333231232221131211a a aa a a a a a M 2.1 对称中心和反演（i ）取晶体中心为原点，将晶体中任一点()z ，y ，x 变成()z -，y -，x - ⎪⎪⎪⎭⎫⎝⎛=1-0001-0001-M2.2 对称面和反映（m ）以0z =作为镜面，将晶体中的任何一点()z ，y ，x 变成()z -y x ，， ⎪⎪⎪⎭⎫ ⎝⎛=1-00010001M2.3 n 次旋转对称轴（n 或者n C ）和n 次旋转反演轴（n ） 2.3.1n 次旋转对称轴（n 或者n C ）若晶体绕某一固定轴旋转角度/n π2=α以后能自身重合，则称该轴为n 次旋转对称轴。

复习：1.正点阵基矢与倒易点阵基矢之间的关系同种正应阵基去如倒易点阵基去的栋量叙为1,系 同种正点阵基央如倒易点阵基水的标■叙为零 2、晶带定律[uvw]的方向：r uvw = u a + V b + w c(hkl)面的法线方向:r*hki = h a* + k b* + 1 c* (h a* + kb* + 1 c*)・ (ua + vb + wc) = Ohu+kv+lw=OUVW 加 k] " h, k, h 2 k 2 12 h 2 k 212 两个晶面同属于一个晶带[uvw](112), (232)一个晶面同属于两个晶带[uvw][321], [111]晶面间距通用公式:h hakcosy cos/Jkh ./1cosy//ak1akcosp——1cosa+ —cos/—cosa+ _ c osy1—a bc cosa1bcos ftb4c1c c os。

cosa b /c11 cosy cos/i cosy 1cos a cosp cos a 1简立方：(cP): a=4 A,面间距：(111)体心立方：: a= 4 A,面间距：(111)立方晶系:简立方1 _ /?2+k2 +/2“ =2cr体心立方/面心立方晶面间距：d简立方/ 2§3-1对称性与对称操作对称元素；对称操作；晶体的对称性晶体外部形态的对称性，通常称为宏观对称性, 点对称性。

晶体内部原子排列的对称性，称为微观对称，1生§3.2晶体的宏观对称元素惯用记号:C; 国1 ＞对称中心际符号:i；熊夫利符号:G2、旋转轴旋转操作;旋转反演、倒反对称轴（旋转轴）基转角:a旋转轴的轴次:n = 3607a旋转矩阵:X2cos a-sin。

0「力= sin a cos a0.0 0 I .Z|.cos a -sin。

0/?；(©)= sin a cos 67 00 0 IN只能是1, 2, 3, 4, 6没有5或者7等更高次c AB 一AC, AD/ AD = AC = ABA -------- •* E AE = m-AB AE = 2-AC-cosaXy Bm = |2-cosa| （m整数，晶体的平移周期D 性）-2 < m < 2m：・2、・1、0^ 1、2,a： 180, 120, 90, 60和360。