用差分方程求系统的单位脉冲响应
- 格式:ppt
- 大小:2.34 MB
- 文档页数:2


第一章1、设某线性时不变离散系统的差分方程为)()1()(310)1(n x n y n y n y =++--,试求它的单位抽样响应。
它是不是因果的?是不是稳定的?2、用两种方法计算下面两个序列的线性卷积:x(n)= δ(n)+2δ(n+2)-δ(n-4) , y(n)= 3δ(n-1)+δ(n-3) 。
3、一阶因果系统的差分方程为 y(n)-ay(n-1)=x(n), a 是实数,求: (1)、该系统的系统函数H (z )和收敛域;(2)、分0<a<1, a=0, a>1三种情况写出h(n)及稳定性,画出零极点分布图。
4、下列是系统的单位脉冲响应表达式,试指出这些系统的因果、稳定性。
(1)、 e R n anN ()(2)、 2nU n ()- (3)、)2()2(++-n n δδ (4)、)(2n U n (5)、 )1(3--n U n (6)、)1(1+n U n5、若azaz z X --=--111)(,1->az ,试求)(z X 的反z 变换。
6、已知某线性时不变系统的单位脉冲响应为()()n h n a u n =,10<<a , 输入序列为()()nx n b u n =,10<<b ,(1) 请用z 域关系式计算该系统的输出序列y (n ); (2) 请分析该系统的因果稳定性。
7、已知某系统的差分方程为)()2(2)1(3)(n x n y n y n y +---=,求:(1)、系统函数 (2)、系统频响 (3)、系统零极点 (4)、收敛域为1<|z|<2时的单位脉冲响应。
8、序列的Z 变换)21)(5.01(5.1)(111------=z zzz X 。
在以下三种收敛域下,哪一种是左边序列?哪一种是右边序列?哪一种是双边序列?并求出各对应的序列。
(1)、| z | > 2 (2)、| z | < 0.5 (3)、0.5 < | z | < 29、已知一线性移不变因果系统,可用如下差分方程描述:)1(21)()1(21)(-+=--n x n x n y n y求:(1)该系统的冲激响应;(2)系统对输入n j e n x ω=)(的响应;(3)系统的频响。

系统响应及系统稳定性实验报告实验课程:数字信号处理实验名称:系统响应及系统稳定性实验时间:12月1日实验设备:电脑、matlab软件实验目的:在matlab 环境下,掌握求系统相应的方法,掌握时域离散系统的时域特性。
实验内容:原理:在时域中,描写系统特性的方法是差分方程和单位脉冲响应,在频域可以用系统函数描述系统特性。
已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应,本实验仅在时域求解。
在计算机上适合用递推法求差分方程的解,最简单的方法是采用MATLAB语言的工具箱函。
也可以用MATLAB语言的工具箱函数conv函数计算输入信号和系统的单位脉冲响应的线性卷积,求出系统的响应。
系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。
重点分析实验系统的稳定性,包括观察系统的暂态响应和稳定响应。
系统的稳定性是指对任意有界的输入信号,系统都能得到有界的系统响应。
或者系统的单位脉冲响应满足绝对可和的条件。
系统的稳定性由其差分方程的系数决定。
实际中检查系统是否稳定,不可能检查系统对所有有界的输入信号,输出是否都是有界输出,或者检查系统的单位脉冲响应满足绝对可和的条件。
可行的方法是在系统的输入端加入单位阶跃序列,如果系统的输出趋近一个常数(包括零),就可以断定系统是稳定的。
系统的稳态输出是指当n→∞时,系统的输出。
如果系统稳定,信号加入系统后,系统输出的开始一段称为暂态效应,随n的加大,幅度趋于稳定,达到稳态输出。
但是在实验中全部都假设系统的初始状态为零。
实验内容:(1)编制程序,包括产生输入信号、单位脉冲响应序列的子程序,以及用filter函数或conv函数求解系统为3输出响应的主程序。
(2)给定一个低通滤波器的差分方程y(n)=0.05x(n)+0.05x(n-1)+0.9y(n-1)输入信号x1(n)=R8(n),x2(n)=u(n)分别求出x1(n)=R8(n),x2(n)=u(n)的系统响应,并画出其波形。

班 级 学号 姓 名 同组人 实验日期 室温 大气压 成 绩实验题目: 实验一 离散时间信号与系统响应 一、实验目的1.观察离散系统的频率响应和单位脉冲响应并学会其应用。
2.掌握用MATLAB 实现线性卷积的方法及差分方程的求解方法。
3.了解数字信号采样率转换过程中的频谱特征。
4.通过观察采样信号的混叠现象,进一步理解奈奎斯特采样频率的意义。
二、实验仪器计算机一台 MATLAB7.0软件三、实验原理在数字信号处理中,离散时间信号通常用序列{x(n)}表示。
离散时间系统在数学上定义为将输入序列x(n)映射成输出序列y(n)的唯一性变换或运算,亦即将一个序列变换成另一个序列的系统。
记为y(n)=T[x(n)],通常将上式表示成图()()[]x n y n T −−−→∙−−−→所示的框图。
算子T[∙]表示变换,对T[∙]加上种种约束条件,就可以定义出各类离散时间系统。
1.频率响应:在工程上进行时域分析和轨迹分析用频率响应法,它是分析和设计系统的一中有效经典的方法。
线性时不变系统输入输出关系y(n)=x(n)*h(n)。
H(ejw)是频率响应,离散时间系统的线性卷积,由理论学习我们可知,对于线性时不变离散系统,任意的输入信号()()()...(1)(1)(0)()(1)(1)...k x n x k n k x n n x n x n δδδδ∞=-∞=-=+-+++-+∑x (n )可以用δ(n )及其位移的线性组合来表示,即,当输入δ(n )时,系统的输出y(n)=h(n)。
2.卷积:y=conv(h,x),计算向量h 和x 的卷积,结果放在y 中。
由系统的线性移不变性质可以得到系统对x(n)的响应y(n)为()()()k y n x k h n k ∞=-∞=-∑,称为离散系统的线性卷积,简记为y(n)=x(n)*h(n),也就是说,通过系统的冲激响应,可以将输入信号与系统的冲激响应进行卷积运算,可求得系统的响应。


第1章 时域离散信号和时域离散系统 1.1.2 重要公式(1) ∞-∞==-=m n h n x m n h m x n y )(*)()()()( 这是一个线性卷积公式, 注意公式中是在-∞~∞之间对m 求和。
如果公式中x(n)和h(n)分别是系统的输入和单位脉冲响应, y(n)是系统输出, 则该式说明系统的输入、 输出和单位脉冲响应之间服从线性卷积关系。
(2)x(n)=x(n)*δ(n)该式说明任何序列与δ(n)的线性卷积等于原序列。
x(n -n0)=x(n)*δ(n -n0)(3)∞-∞=-=k a n k X T X )j j (1)j (ˆs ΩΩΩ这是关于采样定理的重要公式, 根据该公式要求对信号的采样频率要大于等于该信号的最高频率的两倍以上, 才能得到不失真的采样信号。
∞-∞=--=n a a T nT t T nT t nt x t x /)(π]/)(πsin[)()(这是由时域离散信号理想恢复模拟信号的插值公式。
1.2 解线性卷积的方法解线性卷积是数字信号处理中的重要运算。
解线性卷积有三种方法, 即图解法(列表法)、 解析法和在计算机上用MA TLAB 语言求解。
它们各有特点。
图解法(列表法)适合于简单情况, 短序列的线性卷积, 因此考试中常用, 不容易得到封闭解。
解析法适合于用公式表示序列的线性卷积, 得到的是封闭解, 考试中会出现简单情况的解析法求解。
解析法求解过程中, 关键问题是确定求和限, 求和限可以借助于画图确定。
第三种方法适合于用计算机求解一些复杂的较难的线性卷积, 实验中常用。
解线性卷积也可用Z 变换法,以及离散傅里叶变换求解, 这是后面几章的内容。
下面通过例题说明。
设x(n)=R 4(n), h(n)=R 4(n), 求y(n)=x(n)*h(n)。
该题是两个短序列的线性卷积, 可以用图解法(列表法)或者解析法求解。
表1.2.1给出了图解法(列表法), 用公式可表示为y(n)={…, 0, 0, 1, 2, 3, 4, 3, 2, 1, 0, 0, …}下面用解析法求解, 写出卷积公式为∑∞-∞=∞-∞=-=-=m m m n R m R m n h m x n y )()()()()(44在该例题中, R 4(m)的非零区间为0≤m ≤3, R 4(n -m)的非零区间为0≤n -m ≤3,或写成n -3≤m ≤n ,这样y(n)的非零区间要求m 同时满足下面两个不等式:0≤m ≤3 m -3≤m ≤n上面公式表明m 的取值和n 的取值有关, 需要将n 作分段的假设。

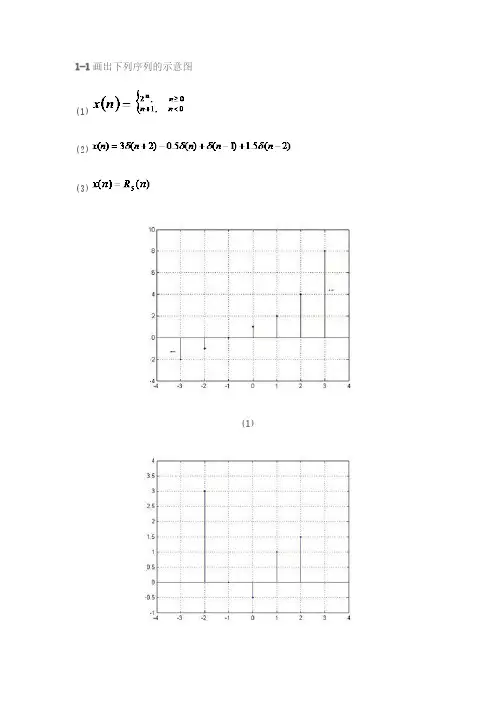

信号分析第二章答案第二章习题参考解答2.1求下列系统的阶跃响应和冲激响应。
(1)y(n)y(n1)某(n)3h(n1)(n)3解当激励为(n)时,响应为h(n),即:h(n)由于方程简单,可利用迭代法求解:h(0)h(1)(0)13,h(1)111h(0)(1)h(0)333,2111h(2)h(1)(2)h(1)333…,由此可归纳出h(n)的表达式:h(n)()n(n)3利用阶跃响应和冲激响应的关系,可以求得阶跃响应:11()n11311(n)h(k)()k[()n](n)1223kk0313nn(2)y(n)y(n2)某(n)4解(a)求冲激响应11h(n2)(n),当n0时,h(n)h(n2)0。
44111特征方程20,解得特征根为1,2所以:42211h(n)C1()nC2()n…(2.1.2.1)2211通过原方程迭代知,h(0)h(2)(0)1,h(1)h(1)(1)0,代入式44h(n)(2.1.2.1)中得:C1C2111C1C2022信号分析与处理的课后习题答案是高等教育出版社的教科书解得C11C22,代入式(2.1.2.1):h(n)12(12)n12(12)n,n0…(2.1.2.2)可验证h(0)满足式(2.1.2.2),所以:h(n)1[(1)n(1222)n](n)(b)求阶跃响应通解为11c(n)C1(2)nC2(2)n特解形式为1p(n)K,p(n2)K,代入原方程有K4K1,完全解为(n)1 14c(n)p(n)C1(2)nC2(2)n3通过原方程迭代之(0)1,(1)1,由此可得C41C23112C1412C231解得C1112,C26。
所以阶跃响应为:(n)h(k)[41111k032(2)n(6)(2)n](n)(3)y(n)某(n)2某(n1)某(n2)解h(n)(n)2(n1)(n2)n(n)h(k)(n)2(n1)(n2)k0(4)dy(t)dt5y(t)某(t)解dh(t)dt5h(t)(t)当t>0时,原方程变为:dh(t)dt5h(t)0。
数字信号处理MATLAB上机实验第一章14(2)已知差分方程为y(n)=1/5(x(n)+x(n-1)+x(n-2)+x(n-3)+x(n-4)),输入信号如下图所示,试求出y(n).实验目的:学习MATLAB的简单使用,学习如何使用MA TLAB绘制信号的波形图。
实验任务:学会调用filter、filtic函数求解差分方程,掌握差分方程的解法以及波形图的绘制方法。
实验思路:实验代码:ys=1;xn=[ones(1,12),[2,1,1,0.5,1,1,1,1.5],ones(1,12)];B=[0.2,0.2,0.2,0.2,0.2];A=1;xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')title('(第14题)');xlabel('n');ylabel('y(n)')运行结果:实验总结:掌握了序列差分方程的求解方法,感受到了MATLAB的强大之处。
了解了使用MATLAB解决数字信号问题的基本形式。
16(1)已知差分方程y(n)=0.6y(n-1)-0.08y(n-2)+x(n),求出系统的单位脉冲响应和单位阶跃响应。
实验目的:掌握用MA TLAB求解差分方程以及MA TLAB对函数的表示。
实验任务:用MATLAB表示冲击函数和阶跃函数,并求出题设差分方程对应的两种响应的波形。
实验思路:实验代码:单位脉冲响应:ys=1;xn=[1,zeros(1,30)];B=1;A=[1,-0.6,0.08];xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')title('(16-1)');xlabel('n');ylabel('h(n)')单位阶跃响应:ys=1;xn=[ones(1,30)];B=1;A=[1,-0.6,0.08];xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')title('(16-2)');xlabel('n');ylabel('u(n)')运行结果:单位脉冲响应单位阶跃响应实验总结:掌握了冲激函数和阶跃函数的波形求解方法,对MA TLAB的使用更加熟练。
第4章 时域离散系统的网络结构习题1. 已知系统用下面差分方程描述:)1(31)()2(81)1(43)(−+−−n x n x n y n y n y +-=试分别画出系统的直接型、 级联型和并联型结构。
式中x (n )和y (n )分别表示系统的输入和输出信号。
2. 设数字滤波器的差分方程为)2(41)1(31)1()()(−+−+−+=n y n y n x n x n y试画出系统的直接型结构。
3. 设系统的差分方程为y (n )=(a +b )y (n -1)-aby (n -2)+x (n -2)+(a +b )x (n -1)+ab式中, |a |<1, |b |<1, x (n )和y (n )分别表示系统的输入和输出信号, 试画出系统的直接型和级联型结构。
4. 设系统的系统函数为)81.09.01)(5.01()414.11)(1(4)(211211−−−−−−++−+−+=z z z z z z z H试画出各种可能的级联型结构, 并指出哪一种最好。
5. 题 5图中画出了四个系统, 试用各子系统的单位脉冲响应分别表示各总系统的单位脉冲响应, 并求其总系统函数。
题 5图6. 题6图中画出了10种不同的流图, 试分别写出它们的系统函数及差分方程。
题6图7. 假设滤波器的单位脉冲响应为h (n )=a n u (n ) 0<a <1求出滤波器的系统函数, 并画出它的直接型结构。
8. 已知系统的单位脉冲响应为h (n )=δ(n )+2δ(n -1)+0.3δ(n -2)+2.5δ(n -3)+0.5δ(n -5)试写出系统的系统函数, 并画出它的直接型结构。
9. 已知FIR 滤波器的系统函数为)9.01.29.01(101)(4321−−−−++++=z z z z z H试画出该滤波器的直接型结构和线性相位结构。
10. 已知FIR 滤波器的单位脉冲响应为:(1) N=6h(0)=h(5)=15h(1)=h(4)=2h(2)=h(3)=3(2) N=7h(0)=h(6)=3h(1)=-h(5)=-2h(2)=-h(4)=1h(3)=0试画出它们的线性相位型结构图,并分别说明它们的幅度特性、相位特性各有什么特点。
长沙理工大学计通学院通信工程系胡双红编数字信号处理A 实验报告实验项目名称:离散时间信号与系统学院:______计算机与通信工程____ 专业:______ _通信工程 _________ 学号:______20xxxxxxxxxx_______ 班级:______ 通信1x-x_________ 报告人:________ xx_____________ 指导老师:___ 胡双红 _ _______ 实验时间:_______201x-x-x________实验目的:1、熟悉常见离散时间信号的产生方法;2、熟悉离散时间系统的单位脉冲响应和单位阶跃响应的求解方法;3、熟悉离散时间信号经过离散时间系统的响应的求解方法。
实验内容:已知离散时间系统差分方程为y(n)-0.5y(n-1)+0.06y(n-2)=x(n)+x(n-1),求1、该系统的单位脉冲响应并绘图;2、该系统的单位阶跃响应并绘图;3、已知x(n)=可自己指定用filter函数经过系统的响应并绘图;4、用convwthn函数求系统响应并绘图。
实验平台:MATLAB集成软件**实验流程:设计流程:1、定义a,b2、用impseq函数生成0~100的单位脉冲函数3、用filter函数表示x(n)的系统响应并画图4、用stepseq函数生成0~100的单位阶跃函数5、用filter函数表示x(n)的系统响应并画图6、生成一个0~100的函数x(n)= exp(-0.5*n)7、用convwthn函数做出系统单位脉冲相应和x(n)= exp(-0.5*n)的卷积和得到系统响应并画出卷积和前101点图形8、用filter函数表示x(n)的系统响应实验代码:(1)b=[1,1];a=[1,-0.5,0.06];n=[-10:25];impz(b,a,n);title('系统的单位脉冲响应');xlabel('n');ylabel('h(n)');(2)n=-10:25;x=(n>=0);b=[1,1];a=[1,-0.5,0.06];s=filter(b,a,x);stem(n,s)title('单位阶跃响');xlable('n');ylable('s(n)');(3)a=[1,-0.5,0.06];b=[1,1];n=-10:120;x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3);s1=filter(b,a,x1);stem(n,s1);xlabel('n');ylabel('s1(n)');(4)a=[1,-0.5,0.06];b=[1,1];n=-20:120;h=impz(b,a,n);x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3); nyb=n(1)+n(1);nye=n(length(x1))+n(length(h));m=[nyb:nye];y=conv(x1,h);stem(m,y);title('系统响应');xlabel('m');ylabel('y(m)');实验结果:单位脉冲响应单位阶跃响应x(n)用filter函数经过系统的响应convwthn函数求系统响应实验心得:实验心得:熟悉了常见离散时间信号的产生方法、离散时间系统的单位脉冲响应和单位阶跃响应的求解方法;熟悉离散时间信号经过离散时间系统的响应的求解方法。
数字信号处理作业组员信息姓名姓名学号吴永斌电气133 201306010324张文超电气131 201306010122吴晨刚电气133 201306070228姚雨电气134 201306010424上机题(第17题)1.求解系统单位脉冲响应hn.(1)问题分析:信号输入xn (单位脉冲序列)经过系统产生输出yn (即hn ),其满足线性常系数差分方程,用filter 函数求解方程即可得到系统的单位脉冲响应hn 。
(2)程序编写:>> %求解系统的单位脉冲响应hn >> xn=[1,zeros(1,49)];>> a1=-0.8;a2=0.64;b=0.886;>> B=[b];A=[1,a1,a2];%差分方程的系数向量>> hn=filter(B,A,xn);%调用filter 解差分方程,得系统的单位脉冲响应hn >> n=0:length(hn)-1; >> stem(n,hn,'.')>> xlabel('n');ylabel('hn');>> title('系统的单位脉冲响应hn');grid; (3)画图如下:1020304050-0.500.51nh n系统的单位脉冲响应hn2.求解系统零状态单位阶跃响应sn.(1)问题分析:信号输入xn (单位阶跃序列)经过系统产生输出yn (即hn ),其满足线性常系数差分方程,由于初始状态为0(即ys=0),先利用filtic 算出由初始条件下等效的输入序列xi,再用filter 函数求解方程即可得到系统的零状态单位阶跃响应sn,通过Matlab 编程及画图可得到相应的响应的结果。
(2)程序编写:>> %系统零状态单位阶跃响应sn >> a1=-0.8;a2=0.64;b=0.886; >> xn=ones(1,101);>> ys=0;B=[b];A=[1,a1,a2]; >> xi=filtic(B,A,ys); >> sn=filter(B,A,xn,xi); >> n=0:length(sn)-1; >> stem(n,sn,'.')>> xlabel('n');ylabel('sn');>> title('零状态单位阶跃响应sn'); grid on ;(3)画图如下:0204060801000.20.40.60.811.21.41.6ns n零状态单位阶跃响应sn上机题(第18题)(1)题意分析:本题用到系统的级联和并联、卷积和求解线性常系数差分方程等知识。