浙江省绍兴县杨汛桥镇中学九年级数学竞赛模拟试题8

20141106九年级数学竞赛1．如图，正方形ABCD的边长为2，⊙O的直径为AD，将正方形沿EC折叠，点B落在圆上的F点，则BE的长为．2．如图，在平面直角坐标系中，直线分别交x轴，y轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．（1）直接写出点A，B的坐标，并求直线AB与CD交点的坐标；（2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点M从点A出发，沿线段AB以每秒个单位长度的速度向终点B运动，过点P作PH⊥OA，垂足为H，连接MP，MH．设点P的运动时间为t秒．①若△MPH与矩形AOCD重合部分的面积为1，求t的值；②点Q是点B关于点A的对称点，问BP+PH+HQ是否有最小值？如果有，求出相应的点P的坐标；如果没有，请说明理由．3．定义：在平面直角坐标系中，过一点分别作坐标轴的垂线，若垂线与坐标轴围成矩形的周长与面积相等，则这个点叫做“和谐点”．如图1，矩形ABOC的周长与面积相等，则点A是“和谐点”（1）判断点E（2，3），F（4，4）是否为“和谐点”；（2）如图2，若点P（a，b）是双曲线y=上的“和谐点”，求满足条件的所有P点坐标．4．给出定义：设一条直线与一条抛物线只有一个公共点，且这条直线与这条抛物线的对称轴不平行，就称直线与抛物线相切，这条直线是抛物线的切线．有下列命题：①直线y=0是抛物线y=x2的切线；②直线x=﹣2与抛物线y=x2相切于点（﹣2，1）；③直线y=x+b与抛物线y=x2相切，则相切于点（2，1）；④若直线y=kx﹣2与抛物线y=x2相切，则实数k=．其中正确命题的是（）A ．①②④B．①③C．②③D．①③④5．已知：在面积为7的梯形ABCD中，AD∥BC，AD=3，BC=4，P为边AD上不与A、D 重合的一动点，Q是边BC上的任意一点，连接AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F，则△PEF面积最大值是．6．如图1，△ABC中，CA=CB，点O在高CH上，OD⊥CA于点D，OE⊥CB于点E，以O为圆心，OD为半径作⊙O．（1）求证：⊙O与CB相切于点E；（2）如图2，若⊙O过点H，且AC=5，AB=6，连接EH，求△BHE的面积和tan∠BHE的值．7．如图，在直角坐标系xOy中，已知A（12，0），B（0，9），C（3，0），D（0，4），Q 为线段AB上一动点，OQ与过O、C、D三点的圆交于点P．问OP•OQ的值是否变化？证明你的结论．8交于点E，PN交CM于点F，设四边形MEPF的面积为S，求S的最大值．9．锐角三角形△ABC的外心为O，外接圆半径为R，延长AO，BO，CO，分别与对边BC，CA，AB交于D，E，F；证明：．10．如图在平面直角坐标系中，直线l平行x轴，交y轴于点A，第一象限内的点B在l上，连结OB，动点P满足∠APQ=90°，PQ交x轴于点C．（1）当动点P与点B重合时，若点B的坐标是（2，1），求P A的长．（2）当动点P在线段OB的延长线上时，若点A的纵坐标与点B的横坐标相等，求P A：PC的值．（3）当动点P在射线OB上时，点D是直线OB与直线CA的交点，点E是直线CP与y轴的交点，若∠ACE=∠AEC，PD=2OD，求P A：PC的值．11．阅读下列材料：在平面直角坐标系中，若点P1（x1，y1）、P2（x2，y2），则P1、P2两点间的距离为．例如：若P 1（3，4）、P2（0，0），则P1、P2两点间的距离为．设⊙O是以原点O为圆心，以1为半径的圆，如果点P（x，y）在⊙O上，那么有等式，即x2+y2=1成立；反过来，如果点P（x，y）的坐标满足等式x2+y2=1，那么点P必在⊙O上，这时，我们就把等式x2+y2=1称为⊙O的方程．解决问题：如图平面上有A（1，0），B（﹣1，0）两点，已知圆心坐标为（3,4）．半径为2. （1）写出已知圆的圆方程；（2）在圆上求一点P1使△ABP1面积最大并求出此面积；（3）求使|AP|2+|BP|2取得最小值时的圆上的点P的坐标．12．已知函数f（x）=ax2+bx+c，且．（1）求证：a＞0且；（2）求证：函数f（x）在区间0<x<2内至少有一个零点；（3）设x1，x2是函数f（x）的两个零点，求|x1﹣x2|的范围13．2位八年级同学和m位九年级同学一起参加象棋比赛，比赛为单循环，即所有参赛者彼此恰好比赛一场．记分规则是：每场比赛胜者得3分，负者得0分；平局各得1分．比赛结束后，所有同学的得分总和为130分，而且平局数不超过比赛局数的一半，则m的值为．。

浙江省绍兴县杨汛桥镇中学2013届九年级数学竞赛模拟试题8 北师大版1、如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=10 m，塔影长DE=28 m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为米。

（）A.30.1B.30.2C.30.3D. 30.42、如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△211B D C的面积为1S，△322B D C的面积为2S，…，△1n n nB D C+的面积为nS，则4S= ；3、如图，直线m上摆着三个正三角形：ABCV、HFGV、DCEV.已知12BC CE=,F、G分别是BC、CE的中点，FM//AC，GN//DC.设图中的三个平行四边形的面积依次为1S、2S、3S，若1310S S+=，则2S=_________.4、兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为（）A．11.5米B．11.75米C．11.8米D．12.25米5、如图，在平行四边形ABCD中，P是AB上的一个动点(不与A、B重合)．连接OP交对角线AC于E连接BE．当△BEC的面积等于平行四边形(第1题)（第4题图）（第7题）ABCD 面积的52时，=BPAP ( ) A 、1:1 B 、1：2 C 、1：3 D 、1：46、数学课上，老师用多媒体给同学们放了2010年春节联欢晚会由魔术界当红艺人刘谦表演的的神奇的障眼法“硬币穿玻璃”魔术，敏捷的身手、幽默的语言把同学们逗得乐不可支。

数学竞赛辅导系列讲座八——相似形1、在正三角形ABC 的边BC 、AC 上分别有点E 、F ，且满足BE=CF=a ， EC=FA=b （a>b ），当BF 平分AE 时，则ab的值为（ ）A 、5-12B 、5-22C 、5+12D 、5+222、设AD 、BE 、CF 为△ABC 的三条高，若AB=6，BC=5，EF=3，则线段BE 的长为（ ）A 、185B 、4C 、215D 、2453、O 是△ABC 的外心，OD ⊥BC ，OE ⊥AC ，OF ⊥AB ，则OD ：OE ：OF=（ ）A 、a ：b ：cB 、1a ：1b ：1c C 、Cos A ：CosB ： CosC D 、SinA ：SinB ：SinC4、如图，△ABC 是边长为6cm 的等边三角形，被一平行于BC 的矩形所截， AB 被截成三等分，则图中阴影部分面积为（ ）A 、4B 、2 3C 、3 3D 、4 35、在等腰直角三角形ABC 的斜边AB 上取两点M 、N ，使∠MCN=45°， 记AM=m ，MN=x ，BN=n ，则以x 、m 、n 为边长的三角形形状是（ ）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、随x 、m 、n 的变化而变化 6、△ABC 中，D 、F 分别在AC 、BC 上，且AB ⊥AC ，AF ⊥BC ，BD=DC=FC=1，则AC=（ ）A 、 2B 、 3C 、32D 、337、Rt △ABC 中，∠C=Rt ∠，CD 是斜边AB 上的高，在BC 和CA 上分别取点E 和F ，使△EFD 和△ABC 相似，这样的△FED 有（ ）个A 、1B 、2C 、3D 、多于38、设锐角△ABC 的三条高AD 、BE 、CF 相交于H ，若BC=a ，AC=b ，AB=c ，则AH ·AC+BH ·BE+CH ·CF 的值是（ ） A 、1()2ab bc ca ++ B 、2221()2a b c ++ C 、2()3ab bc ca ++ D 、2222()3a b c ++ 9、设D 是△ABC 的边AB 上的一点，作DE ∥BC 交AC 于点E ，作DF ∥AC 交B C 于点F ，已知△ADE ，△DBF 的面积为m 和n ，则四边形DECF 的面积为__________． 10、如图，Y ABCD 的对角线相交于O ，在AB 的延长线上任取一点E ，连结OE ，交BC 于F ，若AB=a ，AD=c ，BE=b ，则BF=___________．11、已知△ABC 为锐角三角形，其最大边AC 上有一点P （P 与A 、C 不重合），过P 作直线l ，FACc F OCE使l 截△ABC 所得的三角形与原三角形相似，则这样的直线可以作______条．12、正方形ABCD 边长为1，M 、N 为BD 所在直线上两点，且A M= 5 ，∠MAN=135°，则四边形AMCN 的面积为________．13、如图，已知△ABC 的面积为1，D 为BC 的中点，E 、F 分别在AC 、AB 上，且S △BDF =15，S△CDE=13，则S △DEF =_________． 14、△ABC 中，∠C=90°，D 、E 分别为BC 上的两点，且∠ABC=12 ∠ADC=13 ∠AEC ，若BD=11，DE=5，则AC=______．15、如图，已知边长为a b c -的正方形DEFG 内接于面积为1的正三角形，其中a 、b 、c是整数，且b 不能被任何质数的平方整除，则a cb-=___________．16、如图，△ABC 中，AB=2，AC= 3 ，∠A=∠BCD=45°，则BC 的长为______，△BDC 的面积为______．17、设CD 是Rt △ABC 斜边AB 上的高，I 1、I 2分别是△ADC 、△BDC 的内心，AC=3，BC=4，求I 1I 2．18、如图，在△ABC ，D 、E 分别是AC 、BC 的中点，BF=13AB ，BD 与FC 相交于G ，（1）求证：EG ∥AC ；CABDD B CEFEGADABGEDB CF（2）求BFGBEGS S ∆∆的比值．19、已知线段AB ，只用圆规把线段AB 二等分．20、分别以锐角△ABC 的三边为边向外作正△A BC 、正△BCE 、正△CAF ，三个正三角形的中心分别为O 1、O 2、O 3，求证：△O 1O 2O 3是正三角形．21、如图，在平行四边形ABCD 中，P 1、P 2、……、P n-1分别是BD 的n 等分点，连结AP 2并延长交BC 于点E ，连结AP n-2并延长交CD 于点F ， （1）求证：EF ∥BD ；（2）若平行四边形ABCD 的面积为S ，且S △AEF =38S ，求n 的值．22、是否存在一个边长恰是三个连续正整数，且其中一个内角是另一个内角的2倍的△ABC ？证明你的结论．FADP 1P 2P n-2P n-123、如图，在直角梯形ABCD ，∠ABC=∠BAD=90°，AB=16，对角线AC 与BD 交于点E ，过E 作EF ⊥AB 于点F ，O 为AB 中点，且EF+EO=8，求AD+BC 的值．24、已知点D 在△ABC 的边BC 上，且与B 、C 不重合，过D 作AC 的平行线DE 交AB 于E ，作AB 的平行线DF 交AC 于点F ，又已知BC=5，①设△ABC 的面积为S ，若四边形AEDF 的面积为25 S ，求BD的长；②若AC= 2 AB ，且DF 经过△ABC 的重心G ，求EF 两点间的距离．25、如图，O 是四边形ABCD 对角线交点，已知∠BAD+∠BCA=180°，AB=5，AC=4，AD=3，BODO=76 ，求BC ．26．如图是由四个大小不等的、顶角为120o的等腰三角形拼接而成．已知三角形ABC 面积为100，三角形ACD 面积为33，三角形ABF 面积为35．组成图形的四个等腰三角形中，求最小的一个面积是多少?27．如图在等腰梯形ABCD 中，AD ∥BC ，AD=1，AB=2，E 是CD 上一点，且∠EBC=∠ABD ． （1）若BC=x ，CE=y ．求y 关于x 的函数关系式，并求自变量x 的取值范围；ECDOABDEDCBA（2）连结AE ，是否存在x ，使⊿ABE 与⊿DBC 相似．若存在，求出x 的值；若不存在，请说明理由．28．29．如图，正方形ABCD 和正方形EFGH 中，O 为BC 、FG 的中点，且点F 在正方形ABCD 内，连AE 、BF ，则AE ：BF的值为 ．30．如图所示，在⊿ABC 的两侧向形外作正⊿ABP 和⊿ACQ ，点E 、F 是这两个正三角形的中心，再以EF 为一边向上作正三角形DEF ． 求证：（1）BC=3AD ； （2）AD ⊥BC ．31．如图，射线AM ，BN 都垂直于线段AB ，点E 为AM 上一点，过点A 作BE 的垂线AC 分别交BE ，BN 于点F ，C ，过点C 作AM 的垂线CD ，垂足为D ．若⊿CDFQPFEDCBA为等腰三角形，则AEAD=．32．在⊿ABC中，∠A=024，∠B=030，在边AB上有一点D，使BD=AC，连结CD．求∠BDC的度数．33．（2011年北京市中考）如图在Rt△ABC中，90ACB∠=︒，30BAC∠=︒，AB=2，D是AB边上的一个动点（不与点A、B重合），过点D作CD的垂线交射线CA于点E．设AD x=，CE y=，则下列图象中，能表示y与x的函数关系图象大致是( )34.等腰梯形ABCD中，AD BC∥，BC=42,AD=2，B∠=45°．直角三角板含45°角的顶点E在边BC上移动（不与点C重合），一直角边始终经过点A（如图），斜边与CD交于点F．设BE=x，CF=y，（1）求y关于x的函数解析式，并求出当点E移动到什么位置时y的值最大，最大值是多少？（2）连结AF，当⊿AEF为直角三角形时，求x的值;（3）求点E移动过程中，⊿ADF外接圆半径的最小值.DCBAECABD。

20141101九年级数学竞赛1.如图，在平面直角坐标系中，直角梯形OABC 的顶点A 、B 的坐标分别是(5,0)、(3,2)，点D 在线段OA 上，BD =BA ， 点Q 是线段BD 上一个动点，点P 的坐标是(0,3)，设直线PQ 的解析式为y kx b =+． （1）求k 的取值范围；（2）当k 为取值范围内的最大整数时，若抛物线25y ax ax =-的顶点在直线PQ 、OA 、AB 、BC 围成的四边形内部，求a 的取值范围．2.如图，扇形O M N 的半径为1，圆心角是90°．点B 是MN 上一个动点， BA ⊥OM 于点A ，BC ⊥ON 于点C ，点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点，GF 与CE 相交于点P ，DE 与AG 相交于点Q ． （1）求证：四边形EPGQ 是平行四边形；（2）（2）探索当OA 的长为何值时，四边形EPGQ 是矩形；（3）（3）连结PQ ，试说明223PQ OA +是定值．QP xy DCBAO3．如图在平面直角坐标系xOy 中，8AO =，AB AC =，4sin 5ABC ∠=．CD 与y 轴交于点E ，且COE ADE S S =△△．已知经过B ，C ，E 三点的图象是一条抛物线，求这条抛物线对应的二次函数的解析式．4．如图，⊙O 的内接四边形ABCD 中，AC ，BD 是它的对角线，AC 的中点I 是△ABD 的内心.求证：（1）OI 是△IBD 的接圆的切线； （2）AB +AD =2BD .5如图，分别以边长1为的等边三角形ABC 的顶点为圆心，以其边长为半径作三个等圆，得交点D E F 、、，连接CF 交C 于点G ，以点E 为圆心，EG 长为半径画弧，交边AB 于点M ，求AM 的长。

( 第12题 )IO ACBD6．如图，正方形ABCD 的边长为215，E ，F 分别是AB ，BC 的中点，AF 与DE ，DB 分别交于点M ，N ，则△DMN 的面积是 .7.如图正方形ABCD 的边长为1,Q,R 为边AB 的三等分点,DQ 与CR 交于点E,设过E,A,C 三点的圆交DE 于P,则DP 的长为8.已知△ABC 为钝角三角形，其最大的边AC 上有一点P （P 与A ，C 不重合），过P 作直线l 使l 截△ABC 所得的三角形与原三角形相似，则这样的l 可作______________条.9.在△ABC 中，C B ∠=∠2，AD 为∠A 的角平分线，BD AB 32=（n>m>0).则cosC_________10.抛物线a x ax y 2222++=与直线1+=x y 交于A ，B 两点，若AB 最大，则a=__________.11.在平面直角坐标系xoy 中，我们把横坐标为整数，纵坐标为完成平方数的点称为“好点”，求二次函数y =（x －90）2－4907的图像上的所有“好点”的坐标。

20141109九年级数学竞赛1．已知二次函数f（x）=ax2+bx+c（a＞0））的图象与x轴有两个不同的交点，若f（c）=0，且0＜x＜c时，f（x）＞0（1）证明：是f（x）=0的一个根（2）试比较与c的大小（3）证明：﹣2＜b＜﹣1．2．已知函数f（x）=x2+ax+b．（1）若对任意的实数x，都有f（x）≥2x+a，证明：b≥1；（2）当x∈[﹣1，1]时，f（x）的最大值为b﹣a+1，求a的取值范围；（3）若a=﹣2，关于x的方程|f（x）|=1有4个不相等的实数根，求b的取值范围．3．已知二次函数f（x）=ax2+bx+c．（1）若f（﹣1）=0，试判断函数f（x）零点个数；（2）若对∀x1，x2∈R，且x1＜x2，f（x1）≠f（x2），试证明∃x0∈（x1，x2），使成立．（3）是否存在a，b，c∈R，使f（x）同时满足以下条件①对∀x∈R，f（x﹣4）=f（2﹣x），且f（x）≥0；②对∀x∈R，都有．若存在，求出a，b，c 的值，若不存在，请说明理由．4．已知二次函数f （x ）=ax 2+bx+c ．（1）若f （﹣1）=0，试判断函数f （x ）零点个数；（2）是否存在a ，b ，c ∈R ，使f （x ）同时满足以下条件：①对任意x ∈R ，f （x ﹣4）=f （2﹣x ），且f （x ）≥0；②对任意x ∈R ，都有，若存在，求出a ，b ，c 的值，若不存在，请说明理由．5．设P 为等边△ABC 外接圆的BC 上的一点，求证：PA 2=AB 2+PB •PC ．6．把一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷2次，若两个正面朝上的编号分别为m ，n ，则二次函数2y x mx n =++的图象与x 轴有两个不同交点的概率是（ ）．（A ）512 （B ）49 （C ）1736（D ）127．是否存在一个三边长恰是三个连续正整数，且其中一个内角等于另一个内角2倍的△ABC ？证明你的结论．8．如图，E点为x轴正半轴上一点，⊙E交x轴于A、B两点，交y轴于C、D两点，P点为劣弧上一个动点，且A（﹣1，0），E（1，0）．（1）如图1，求点C的坐标；（2）如图2，连接PA，PC．若CQ平分∠PCD交PA于Q点，当P点在运动时，线段AQ 的长度是否发生变化；若不变求出其值，若发生变化，求出变化的范围；（3）如图3，连接PD，当P点在运动时（不与B、C两点重合），给出下列两个结论：①的值不变，②的值不变，其中有且只有一个是正确的，请你判断哪一个是正确的，并求其值．9.如图△ABC是等边三角形，延长BC至D，BA至E，使得AE=BD，连接DE，CE若∠BEC=20°则∠CED的度数为( )A 40°B 30°C 20°D 25 °10．a是大于0的实数，已知存在唯一实数k，使得关于x的二次方程x2 + （k2 + ak）x +1999 + k2 + ak = 0的两个根均为质数，求a的值。

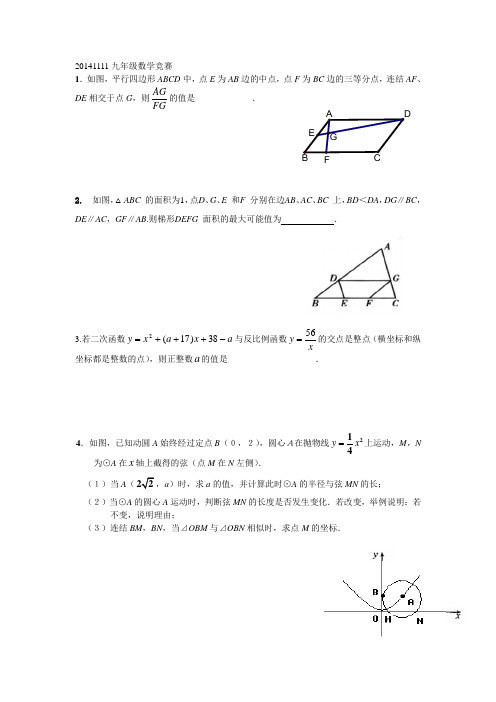
20141111九年级数学竞赛1．如图，平行四边形ABCD 中，点E 为AB 边的中点，点F 为BC 边的三等分点，连结AF 、DE 相交于点G ，则AGFG的值是_____________．2. 如图，△ABC 的面积为1，点D 、G 、E 和F 分别在边AB 、AC 、BC 上，BD ＜DA ，DG ∥BC ，DE ∥AC ，GF ∥AB .则梯形DEFG 面积的最大可能值为 ．3.若二次函数a x a x y -+++=38)17(2与反比例函数xy 56=的交点是整点（横坐标和纵坐标都是整数的点），则正整数a 的值是____________________．4．如图，已知动圆A 始终经过定点B （０，２），圆心Ａ在抛物线y x =214上运动，M ，N 为⊙A 在x 轴上截得的弦（点M 在N 左侧）．（１）当A （22，a ）时，求a 的值，并计算此时⊙A 的半径与弦MN 的长； （２）当⊙A 的圆心A 运动时，判断弦MN 的长度是否发生变化．若改变，举例说明；若不变，说明理由；（３）连结BM ，BN ，当⊿OBM 与⊿OBN 相似时，求点M 的坐标．GA BDCE F图5．在△ABC 中，AB>AC ，∠A 的外角平分线交△ABC 的外接圆于D ，DE⊥AB 于E ， 求证：AE=．6、对于二次函数2y ax bx c =++，如果当x 取任意整数时，函数值y 都是整数，那么我们把该函数的图象叫做整点抛物线（例如：222y x x =++）．（1）请你写出一个二次项系数的绝对值小于1的整点抛物线的解析式 ． （2）请探索：是否存在二次项系数的绝对值小于12的整点抛物线？若存在，请写出其中一条抛物线的解析式；若不存在，请说明理由．7、如图一，等边ABC ∆中，D 是AB 边上的动点，以CD 为一边，向上作等边EDC ∆，连结AE 。

求∠CAE 的度数；（2）如图二，将（1）中等边ABC ∆的形状改成以BC 为底边的等腰三角形，顶角∠BAC=300，所作等边EDC ∆改成已DC 为底边的等腰三角形，且相似于ABC ∆。

数学参考答案一、选择题 题号 1 2 3 4 5 6 7 8 9 10 答案 ABCAACDDCC二、填空题11．)2)(2(y x y x -+ 12． 413． ⎪⎩⎪⎨⎧=+=+2535y x y x 14． 15°，105°15． ），（3232 16． 29三、解答题17．（1）计算：οsin30)2019(2301--+--．=1131222+--= （4分） （2）解方程：0322=--x x ．11-=x ，32=x （4分）18．（1）50（2分+2分）（2）72°（2分） （3）P =31（2分）乒乓球球球羽毛球足球5912101419．（答案不唯一）（2分+3分+3分）20．（1）62≤≤t ． （4分） （2）t S 4=，t 46=，23=t ． （2分） 202+-=t S ，2026+-=t ，7=t ． （2分）21．（1）∵斜坡CM 的坡比i ＝1：3，∴DM=3CD=6m ． （5分） （2）过点C 作CE ⊥AB ，垂足为E ，设BM =x ，3tan60==BMABο，x AB 3= 23-=x AE ，6+=x CE ，33623tan30=+-==x x CE AE ο 33+=x ，∴333+=AB ． （5分）22．点P (a ．6a -+)，a PD =，6+-=a PC ．（1）① 周长=12)]6([2=+-+a a ． （4分）② 面积=a a a a 6)6(2+-=+-，最大值为9． （4分） （2）a ka ka a S 6)6(2+=+=． 最大值为6436=-k ，23-=k ．（2分） 由对称性可得：23=k ． （2分） 综上，23±=k ．图1：以点A 为顶点的直角三角形图3：以点A 为对角线交 点的平行四边形图2：以点A 为顶点的 平行四边形AA A E23．（1）答案不唯一． （4分）（2）作BC 的中线AD ，勾股定理可得：BC =4，BD =2，则AD =4，∴BC =AD ，∴△ABC 是“和谐三角形”． （4分）（3）点M （2a a ，-），N （2a a ，）． 易知△OMN 为等腰三角形．①边MN 上的中线等于MN ，即22a a = 2=a ，N （2，4）． （2分） ②边OM 上的中线PN 等于OM ，P （222a a ，-）， 422222)2()2(a a a a a a +=-+--， 42424149a a a a +=+，424345a a = 315=a ，N （315，35）． （2分） 综上，N 1（2，4），N 2（315，35） ． 24．（1）①当∠BDE ＝∠BFE ＝45°时，△ABD 为等腰直角三角形，BD=AB=6．（4分）② （Ⅰ） BF =BE ．BD 平分∠FBE ，∠C ＝∠FBD=∠EBD=∠BAD ， ∴△ABD ∽△CBA ，BABCBD BA =，29=BD ． （2分）ABCDP（Ⅱ） BF =EF ．连结FD 并延长交AC 于点H ， ∵BD 是直径 ∴∠BFD =90° ∵BF ∥AC∴∠AHD =∠CHD =∠BFD =90° ∵BF =EF∴∠FBE =∠FEB =∠FDE =∠CDH ∵四边形BEDF 内接于圆 ∴∠FBE =∠ADH ∴∠CDH =∠ADH ∵DH =DH∴△CDH ≌△ADH ∴CD =AD可得BD 2+62=（8-BD ）2 47=BD（2分） （Ⅲ） BE =EF ．连结FD 并延长交AC 于点H ， ∵BD 是直径 ∴∠BFD =90° ∵BF ∥AC∴∠AHD =∠CHD =∠BFD =∠ABD =90° ∵BE =EF∴∠FBE =∠EFB =∠BDA ∵四边形BEDF 内接于圆 ∴∠FBE =∠ADH ∴∠BDA =∠ADH ∵DA =DA∴△ADB ≌△ADH ∴BD=DH ，AH=AB=6由勾股定理可得42+BD 2=（8-BD ）2BD =3 （2分） （2）215-（提示：连结EF ，EM ．可得EM 垂直平分AF ，即EF =AE ，利用△BCE ∽△ACB 得到AE CE 的值，利用射影定理可得AECE k =2）（4分）。

y 竞赛模拟卷1、在△ABC 中，a 、b 、c 分别为角A 、B 、C 的对边，若∠B ＝60°，则bc ab ac +++的值为 （ ）A. 21B. 22C. 1D. 22、.已知a ＝1999x ＋2000，b ＝1999x ＋2001，c ＝1999x ＋2018，则多项式a 2+b 2+c 2-ab-bc-ca 的值为（ ） A. 0 B. 1 C. 2 D. 3 3、已知实数z 、y 、z 满足x+y=5及z 2=xy+y-9，则x+2y+3z=_______________ 4、如图8-8，在△ABC 中，∠ABC ＝60°，点P 是△ABC 内的一点，使得∠APB ＝∠BPC ＝∠CPA ，且PA ＝8，PC ＝6，则PB ＝＿＿5、O 为△ABC 内一点，AO 、BO 、CO 及其延长线把△ABC 分成六个小三角形，它们的面积如图9-7所示，则S △ABC ＝（ ） A. 292 B. 315 C. 322 D. 3576．已知关于x 的方程x 3－ax 2－2ax +a 2－1=0有且只有一个实数根. 求实数a 的取值范围.7．如图所示，在平面直角坐标系中有点A （-1，0）、点B （4，0），以AB 为直径的半圆交y 轴正半轴于点C 。

（1）求点C 的坐标；（2）求过A 、B 、C 三点的抛物线的解析式；（3）在（2）的条件下，若在抛物线上有一点D ，使四边形BOCD 为直角梯形，求直线BD 的解析式。

图8-8BC 图9-7O AB C DEM 第17题图 H8．如图，⊙O 为△ABC 的外接圆，∠BAC=60°，H 为边AC 、AB 上高BD 、CE 的交点，在BD上取点M ，使BM=CH 。

（1）求证：∠BOC=∠BHC；（2）求证：△BOM≌△COH；（3）求MHOH 的值.9．一个棋盘有13行17列，每个小方格里都写了一个数，从左上角开始，第一行依次为1,2, ⋅⋅⋅, 17；第二行依次为18, 19, ⋅⋅⋅, 34; ⋅⋅⋅，一直写到最后一行，现将此棋盘里的数重写，从左上角开始，第一列从上到下依次为1, 2, ⋅⋅⋅ , 13；第二列从上到下依次为14, 15, ⋅⋅⋅, 26；⋅⋅⋅，一直写到最后一列，这样有一些小方格在两种写法里有相同的数，求所有这些小方格里（有相同数的）的数之和是多少？10、如图9-16ABCD 中，P 1、P 2、P 3……P n-1是BD 的n 等分点，连结AP 2，并延长交BC 于点E ，连结AP n-2并延长交CD 于点F 。

1、二次函数的图象如图，若一元二次方程20ax bx m++=有实数根，则m的最大值为（）A．3-B．3 C．6-D．92．如图，两个反比例函数1yx=和2yx=-的图象分别是1l和2l．设点P在1l上，PC⊥x轴，垂足为C，交2l于点A，PD⊥y轴，垂足为D，交2l于点B，则三角形PAB的面积为（）A、3B、4C、92D、53. 如图，过点C(1,2)分别作x轴、y轴的平行线，交直线y=－x+6于A、B两点，若反比例函数xky=(x>0)的图象与△ABC有公共点，则k的取值范围是（）A、2≤k≤9B、2≤k≤8C、2≤k≤5D、5≤k≤84．如图，AB是⊙O的直径，CD是弦，若AB=10cm，CD＝8cm，那么A、B两点到直线CD的距离之和为( )A．12cm B．10cm C． 8cm D．6cm5．一种花边是由如图的弓形组成的，ACB的半径为5，弦AB＝8，则弓形的高CD为( )A．2 B．25C．3 D．3166、.二次函数y=ax2+bx+1（a≠0）的图象的顶点在第一象限，且过点（﹣1，0）．设t=a+b+1，则t值的变化范围是（）A、0＜t＜1B、0＜t＜2C、1＜t＜2D、﹣1＜t＜17、下列命题错误的是（）A．平分弧的直径平分这条弧所对的弦 B．平分弦的直径平分这条弦所对的弧C．垂直于弦的直径平分这条弦 D．弦的中垂线经经过圆心8、小明从图所示的二次函数2y ax bx c=++的图象中，观察得出了下面五2-1-012yx13x=ABCDEFOP条信息：①c ＜0；②abc ＞0；③a-b+c ＞0；④2a-3b=0；⑤c-4b ＞0， 你认为其中 正确信息的个数有（ ）A ．2个 B ．3个C ．4个D ．5个9．点E 为正方形ABCD 的BC 边的中点，动点F 在对角线AC 上运动，连接BF 、EF ．设AF ＝x ，△BEF 的周长为y ，那么能表示y 与x 的函数关系的图象大致是（ ） 10．在边长为2的正方形ABCD 中，对角线AC 与BD 相交于点O ， P 是BD 上一动点，过P 作EF ∥AC ，分别交正方形的两条边于点E 、F . 设BP =x ，△BEF 的面积为y ，则能反映y 与x 之间关系的图象为 （ ）11．如图6，抛物线21(2)3y a x =+-与221(3)12y x =-+交于点(13)A ，，过点A 作x 轴的平行线，分别交两条抛物线于点B C ，．则以下结论： ①无论x 取何值，2y 的值总是正数．②1a =． ③当0x =时，214y y -=．④23AB AC =．其中正确结论是（ ）A ．①② Ｂ．②③ Ｃ．③④ Ｄ．①④12．如图,已知抛物线y 1=－2x 2＋2，直线y 2=2x +2，当x 任取一值时,x 对应的函数值分别为y 1、y 2.若y 1≠y 2，取y 1、y 2中的较小值记为M ；若y 1=y 2，记M = y 1=y 2.例如：当x =1时，y 1=0，y 2=4， y 1＜y 2，此时M =0. 下列判断：①当x ＞0时，y 1＞y 2； ②当x ＜0时，x 值越大，M 值越小； ③使得M 大于2的x 值不存在； ④使得M =1的x 值是 12-或 22.其中正确的是（ ）A. ①② B.①④ C.②③ D.③④ 二. 认真填一填（ 每小题5分，共30分）13、如图，正方形OABC ，ADEF 的顶点A ，D ，C 在坐标轴上，点F 在AB 上，点OxOOOxxxyyyyABCDABCDF E22x y22 C22x y 2 02 A22xy22 D22x y22BABCD O x y B ，E 在函数1(0)y x x=>的图象上，则点E 的坐标是 14．开口向下的抛物线22(2)21y m x mx =-++的对称轴经过点(13)-，，则m =．14（2）把二次函数2)1(2+-=x y 的图象绕原点旋转180°后得到的图象解析式为_______ 15、如图，在平面直角坐标系中，二次函数y =ax 2+c （a <0）的图象过正方形ABOC 的三个顶点A 、B 、C ，则ac 的值是 .16、如图，已知动点A 在函数4(0)y x x=>的图象上， AB x ⊥轴于点B ，AC y ⊥轴于点C ，延长CA 至点D ，使AD =AB ，延长BA 至点E ，使AE =AC 。

竞赛辅导试题1.若把函数y=x 的图象用E （x ，x ）记，函数y=2x+1的图象用E （x ，2x+1）记，……则E （x ，122+-x x ）可以由E （x ，2x ）怎样平移得到？A ．向上平移１个单位B ．向下平移１个单位C ．向左平移１个单位D ．向右平移１个单位2.二次函数y =ax 2+bx +c （a ≠0）的图象如图所示，下列结论①a 、b 异号；②当x =1和x=3时，函数值相等；③4a +b =0，④当y =4时，x 的取值只能为0．结论正确的个数有（ ） 个A ．1 Ｂ．2 Ｃ．3 Ｄ．43..设a 、b 是常数，且b ＞0，抛物线y=ax 2+bx +a 2-5a -6为下图中四个图象之一，则a 的值为（ ）A. 6或－1B. －6或1C. 6D. －14.平面直角坐标系中，若平移二次函数y=(x-2009)(x-2010)+4的图象，使其与x 轴交于两点，且此两点的距离为1个单位，则平移方式为 A ．向上平移4个单位 B ．向下平移4个单位 C ．向左平移4个单位 D ．向右平移4个单位5.已知抛物线103:2-==x x y C ，将抛物线C 平移得到抛物线C '若两条抛物线C 、C ' 关于直线1=x 对称，则下列平移方法中，正确的是 A ．将抛物线C 向右平移25个单位 B ．将抛物线C 向右平移3个单位C ．将抛物线C 向右平移5个单位D ．将抛物线C 向右平移6个单位6.已知函数))((3n x m x y ---=，并且b a ,是方程0))((3=---n x m x 的两个根，则实数b a n m ,,,的大小关系可能是A ．n b a m <<<B ．b n a m <<<C ．n b m a <<<D ．b n m a <<< 7定义[,,a b c ]为函数2y ax bx c =++的特征数, 下面给出特征数为 [2m ，1 – m , –1–m ]的函数的一些结论：① 当m = – 3时，函数图象的顶点坐标是(31，38)；② 当m > 0时，函数图象截x 轴所得的线段长度大于23； ③ 当m < 0时，函数在x >41时，y 随x 的增大而减小； ④ 当m ≠ 0时，函数图象经过同一个点. 其中正确的结论有A. ①②③④B. ①②④C. ①③④D. ②④ 8.已知二次函数cbx ax y ++=2的图象如图所示,记b ac b a q b a c b a p -+++=+++-=2,2,则p 与q 的大小关系为( )A.q p >B.q P =C.q p <D.p 、q 大小关系不能确定9. 如图，四边形ABCD 中，∠BAD =∠ACB =90°，AB =AD ，AC =4BC ，设CD 的长为x ，四边形ABCD 的面积为y ，则y 与x 之间的函数关系式是（ ） A ．2225y x =B ．2425y x =C ．225y x =D ．245y x = 10.已知二次函数2y ax bx c =++(0a ≠)的图象如图所示，有下列结论：①240b ac ->；②0abc >；③80a c +>；④930a b c ++<． 其中，正确结论的个数是11.已知二次函数2y ax bx c =++的图象与x 轴交于点(20)-，、1(0)x ，，且112x <<，与y轴的正半轴的交点在(02)，的下方．下列结论：①420a b c -+=；②0a b <<；③20a c +>；④210a b -+>．其中正确结论的个数是 个．12.将抛物线221216y x x =-+绕它的顶点旋转180°，所得抛物线的解析式是（ ）． A ．221216y x x =--+ B ．221216y x x =-+-ABC DC ．221219y x x =-+-D ．221220y x x =-+-13.y=x 2＋（1－a ）x ＋1是关于x 的二次函数，当x 的取值范围是1≤x ≤3时，y 在x ＝1时取得最大值，则实数a 的取值范围是（ ）。