新人教版八年级数学上册同步测试:14-2-1 乘法公式(无答案)
- 格式:doc
- 大小:50.00 KB
- 文档页数:2
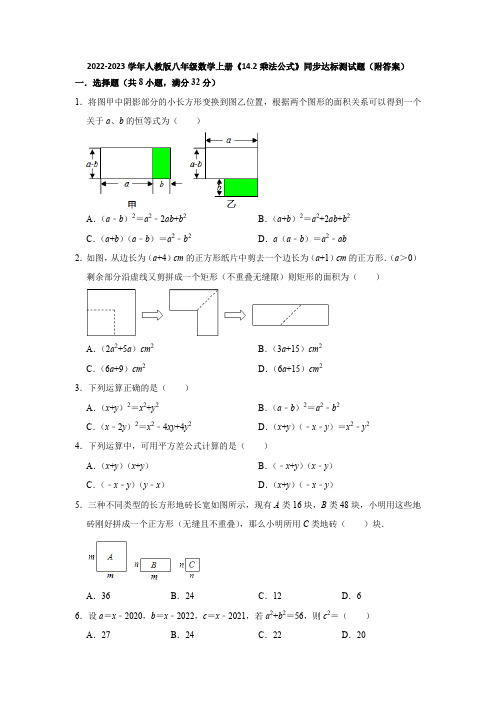
2022-2023学年人教版八年级数学上册《14.2乘法公式》同步达标测试题(附答案)一.选择题(共8小题,满分32分)1.将图甲中阴影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于a、b的恒等式为()A.(a﹣b)2=a2﹣2ab+b2B.(a+b)2=a2+2ab+b2C.(a+b)(a﹣b)=a2﹣b2D.a(a﹣b)=a2﹣ab2.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形.(a>0)剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙)则矩形的面积为()A.(2a2+5a)cm2B.(3a+15)cm2C.(6a+9)cm2D.(6a+15)cm23.下列运算正确的是()A.(x+y)2=x2+y2B.(a﹣b)2=a2﹣b2C.(x﹣2y)2=x2﹣4xy+4y2D.(x+y)(﹣x﹣y)=x2﹣y24.下列运算中,可用平方差公式计算的是()A.(x+y)(x+y)B.(﹣x+y)(x﹣y)C.(﹣x﹣y)(y﹣x)D.(x+y)(﹣x﹣y)5.三种不同类型的长方形地砖长宽如图所示,现有A类16块,B类48块,小明用这些地砖刚好拼成一个正方形(无缝且不重叠),那么小明所用C类地砖()块.A.36B.24C.12D.66.设a=x﹣2020,b=x﹣2022,c=x﹣2021,若a2+b2=56,则c2=()A.27B.24C.22D.207.已知多项式4x2﹣2(m+1)x+1是完全平方式,则m的值为()A.﹣3或1B.﹣3C.1D.3或﹣18.如图,两个正方形边长分别为a,b,已知a+b=11,ab=9,则阴影部分的面积为()A.46B.47C.48D.49二.填空题(共9小题,满分36分)9.(x﹣y)2=(x+y)2+.10.已知(a﹣b)2=13,ab=6,则a2+b2=.11.已知(x+y)2=5,(x﹣y)2=1,则xy=.12.已知a+=3,则a2+的值是.13.若多项式x2+ax+36是一个完全平方式,则常数a的值为.14.如果关于x的多项式x2+8x+b是一个完全平方式,那么b=.15.如果x2﹣Mx+9是一个完全平方式,则M的值是.16.已知m2+n2﹣6m+10n+34=0,则m+n=.17.我国古代数学中“杨辉三角”非常有名.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排序)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数:第四行的四个数1,3,3,1恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等,利用上面的规律计算:95+5×94+10×93+10×92+5×9+1=.三.解答题(共6小题,满分52分)18.计算:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y).19.(﹣2y+1)2﹣(2y+1)(2y﹣1).20.已知多项式A=x2+2x+n2,多项式B=2x2+4x+3n2+3.(1)若多项式x2+2x+n2是完全平方式,则n=;(2)已知x=m时,多项式x2+2x+n2的值为﹣1,则x=﹣m时,该多项式的值为多少?(3)判断多项式A与B的大小关系并说明理由21.阅读材料解决问题.“作差法”是常见的比较数(式)大小的一种方法,即要比较代数式M,N的大小,只要计算出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.例如:比较2a2,a2﹣1的大小:∵2a2﹣(a2﹣1)=a2+1>0∴2a2>a2﹣1根据材料解决以下问题:(1)已知n为自然数,P=(n+1)(n+4),Q=(n+2)(n+3),比较P,Q大小;(2)已知A=202401×202407,B=202403×202405,比较A,B大小.22.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.(1)你认为图2中的阴影部分的正方形的边长等于?(2)请用两种不同的方法求图2中阴影部分的面积.①;②.(3)观察图2你能写出下列三个代数式之间的等量关系吗?(m+n)2,(m﹣n)2,mn.(4)运用你所得到的公式,计算若mn=﹣2,m﹣n=4,求(m+n)2的值.(5)用完全平方公式和非负数的性质求代数式x2+2x+y2﹣4y+7的最小值.23.综合与实践我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.小明同学用如图1所示不同颜色的正方形与长方形纸片拼成了一个如图2所示的正方形.(1)用不同的代数式表示图2中阴影部分的面积,写出你能得到的等式,并用乘法公式说明这个等式成立;(2)小明想到利用(1)中得到的等式可以完成了下面这道题:如果x满足(6﹣x)(x﹣2)=3.求(6﹣x)2+(x﹣2)2的值.小明想:如果设6﹣x=m,x﹣2=n,那要求的式子就可以写成m2+n2了,请你按照小明的思路完成这道题目.(3)如图3,在长方形ABCD中,AB=10,BC=6,E、F是BC,CD上的点,且BE=DF=x,分别以FC,CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为40,求图中阴影部分的面积和.参考答案一.选择题(共8小题,满分32分)1.解:图甲面积=(a﹣b)(a+b),图乙面积=a(a﹣b+b)﹣b×b=a2﹣b2,∵两图形的面积相等,∴关于a、b的恒等式为:(a+b)(a﹣b)=a2﹣b2.故选:C.2.解:长方形的面积为:(a+4)2﹣(a+1)2=(a+4+a+1)(a+4﹣a﹣1)=3(2a+5)=6a+15(cm2).答:矩形的面积是(6a+15)cm2.故选:D.3.解:∵(x+y)2=x2+2xy+y2,∴选项A不符合题意;∵(a﹣b)2=a2﹣2ab+b2,∴选项B不符合题意;∵(x﹣2y)2=x2﹣4xy+4y2,∴选项C符合题意;∵(x+y)(﹣x﹣y)=﹣(x+y)2=﹣(x2+2xy+y2)=﹣x2﹣2xy﹣y2,∴选项D不符合题意,故选:C.4.解:A、含x、y的项都符号相同,不能用平方差公式计算,故本选项错误;B、(﹣x+y)(x﹣y)=﹣(x﹣y)(x﹣y),含x、y的项都符号相同,不能用平方差公式计算,故本选项错误;C、(﹣x﹣y)(y﹣x)=(x+y)(x﹣y),含x的项符号相同,含y的项符号相反,能用平方差公式计算,故本选项正确;D、(x+y)(﹣x﹣y)=﹣(x+y)(x+y),含x、y的项都符号相同,不能用平方差公式计算,故本选项错误;故选:C.5.解:∵16m2+48mn+36n2=(4m+6n)2,∴(4m+6n)2=16m2+48mn+36n2,∴A类16块,B类48块,C类36块刚好拼成一个边长为(4m+6n)的正方形.故选:A.6.解:∵a=x﹣2020,b=x﹣2022,c=x﹣2021,∴a=c+1,b=c﹣1,∵a2+b2=56,∴(c+1)2+(c﹣1)2=56,∴c2=27.故选:A.7.解:∵4x2﹣2(m+1)x+1是完全平方式,∴﹣2(m+1)x=±2•2x•1,解得:m=﹣3或1.故选:A.8.解:a²﹣(a﹣b)b=a²﹣ab+b²=(a²﹣ab+b²)=[(a+b)²﹣3ab]=(121﹣27)=47;故选:B.二.填空题(共9小题,满分36分)9.解:∵(x﹣y)2=x2﹣2xy+y2,(x+y)2=x2+2xy+y2,∴(x﹣y)2=(x+y)2+(﹣4xy).故答案为:﹣4xy.10.解:∵(a﹣b)2=13,ab=6,∴a2+b2=(a﹣b)2+2ab=13+12=25.故答案为:25.11.解:∵(x+y)2=5,(x﹣y)2=1,∴(x+y)2﹣(x﹣y)2=4xy,即5﹣1=4xy则xy=1,故答案为:1.12.解:∵a+=3,∴a2+2+=9,∴a2+=9﹣2=7.故答案为:7.13.解:∵x2+ax+36=x2+ax+62,∴ax=±2×x×6,解得a=±12.故答案为:±12.14.解:x2+8x+b=x2+2•x•4+b,∵关于x的多项式x2+8x+b是一个完全平方式,∴b=42=16,故答案为:16.15.解:∵x2﹣Mx+9是一个完全平方式,∴﹣M=±6,解得:M=±6,故答案为:±6.16.解:根据题意,m2+n2﹣6m+10n+34=0,变形后:(m﹣3)2+(n+5)2=0;得m=3,n=﹣5;所以,m+n=﹣2.17.解:根据题意得:(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;令上式中a=9,b=1,得:95+5×94+10×93+10×92+5×9+1=(9+1)5=105.故答案为:105.三.解答题(共6小题,满分52分)18.解:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y)=9x2+9xy﹣2xy﹣2y2﹣(9x2﹣y2)=9x2+9xy﹣2xy﹣2y2﹣9x2+y2=7xy﹣y2.19.解:原式=4y2﹣4y+1﹣(4y2﹣1)=4y2﹣4y+1﹣4y2+1=﹣4y+2.20.解:(1)∵x2+2x+n2是一个完全平方式,∴n2=1,∴n=±1.故答案为:1或﹣1;(2)当x=m时m2+2m+n2=﹣1,∴m2+2m+1+n2=0,∴(m+1)2+n2=0,∵(m+1)2≥0,n2≥0,∴x=m=﹣1,n=0,∴x=﹣m时,多项式x2+2x+n2的值为m2﹣2m+n2=3;(3)B>A.理由如下:B﹣A=2x2+4x+3n2+3﹣(x2+2x+n2)=x2+2x+2n2+3=(x+1)2+2n2+2,∵(x+1)2≥0,2n2≥0,∴(x+1)2+2n2+2>0,∴B>A.21.解:(1)∵P﹣Q=(n+1)(n+4)﹣(n+2)(n+3)=n2+5n+4﹣n2﹣5n﹣6=﹣2<0,∴P<Q;(2)∵A﹣B=202401×202407﹣202403×202405=(202404﹣3)(202404+3)﹣(202404﹣1)(202404+1)=2024042﹣9﹣2024042+1=﹣8,∴A<B.22.解:(1)由图可知,阴影部分小正方形的边长为:m﹣n;(2)根据正方形的面积公式,阴影部分的面积为(m﹣n)2,还可以表示为(m+n)2﹣4mn;(3)根据阴影部分的面积相等,(m﹣n)2=(m+n)2﹣4mn;n=﹣2,m﹣n=4,∴(m+n)2=(m﹣n)2+4mn=42+4×(﹣2)=16﹣8=8;(5)x2+2x+y2﹣4y+7,=x2+2x+1+y2﹣4y+4+2,=(x+1)2+(y﹣2)2+2,∵(x+1)2≥0,(y﹣2)2≥0,∴(x+1)2+(y﹣2)2≥2,∴当x=﹣1,y=2时,代数式x2+2x+y2﹣4y+7的最小值是2.故答案为:(1)m﹣n;(2)(m﹣n)2,(m+n)2﹣4mn;(3)(m﹣n)2=(m+n)2﹣4mn.23.解:(1)图2中阴影部分的面积为两个正方形的面积和,即a2+b2,图2中阴影部分的面积也可以看作大正方形的面积与两个长方形的面积差,即(a+b)2﹣2ab,由于两次都是阴影部分的面积,因此有:a2+b2=(a+b)2﹣2ab;理由:(a+b)2﹣2ab=a2+2ab+b2﹣2ab=a2+b2;(2)设6﹣x=m,x﹣2=n,则(6﹣x)(x﹣2)=mn=3,m+n=6﹣x+x﹣2=4,∴(6﹣x)2+(x﹣2)2=m2+n2=(m+n)2﹣2mn=42﹣2×3=16﹣6=10;(3)∵AB=10,BC=6,BE=DF=x,∴FC=AB﹣DF=10﹣x,EC=BC﹣BE=6﹣x,∵长方形CEPF的面积为40,即有:(10﹣x)(6﹣x)=40,设10﹣x=m,6﹣x=n,则m﹣n=(10﹣x)﹣(6﹣x)=4,mn=40,∴(m﹣n)2=m2﹣2mn+n2=16,∴m2+n2=16+2mn=16+2×40=96,∵四边形CFGH和CEMN均是正方形,∴图中阴影部分的面积和是:(10﹣x)2+(6﹣x)2=m2+n2=96.。

八年级数学14.2乘法公式练习卷一、选择题:1、平方差公式(a+b )(a -b )= a 2-b 2中字母a ,b 表示( )A .只能是数B .只能是单项式C .只能是多项式D .以上都可以 2、下列多项式的乘法中,可以用平方差公式计算的是( ) A .(a+b )(b+a ) B .(-a+b )(a -b ) C .(13a+b )(b -13a ) D .(a 2-b )(b 2+a ) 3、下列计算中,错误的有( )①(3a+4)(3a -4)=9a 2-4;①(2a 2-b )(2a 2+b )=4a 2-b 2;①(3-x )(x+3)=x 2-9;①(-x+y )·(x+y )=-(x -y )(x+y )=-x 2-y 2. A .1个 B .2个 C .3个 D .4个4、若x 2-y 2=30,且x -y=-5,则x+y 的值是( )A .5B .6C .-6D .-55、下列运算正确的是( ) A .a 3+a 3=3a 6 B .()()=-⋅-53a a -a 8C .(-2a 2b )·4a=-24a 6b 3D .(-13a -4b )(13a -4b )=16b 2-19a 26、若x 2-x -m=(x -m)(x+1)且x≠0,则m 等于( ) A.-1 B.0 C.1D.27、(x +q )与(x +51)的积不含x 的一次项,猜测q 应是( ) A.5B.51C.-51 D.-5 8、设(x m -1y n +2)·(x 5m y -2)=x 5y 3,则m n 的值为( ) A.1B.-1C.3D.-39、计算[(a 2-b 2)(a 2+b 2)]2等于( )A.a 4-2a 2b 2+b 4B.a 6+2a 4b 4+b 6C.a 6-2a 4b 4+b 6D.a 8-2a 4b 4+b 810、已知(a+b)2=11,ab=2,则(a -b)2的值是( )A.11B.3C.5D.1911、若x 2-7xy+M 是一个完全平方式,那么M 是( ) A.27y 2B.249y 2C.449y 2D.49y 212、若x,y 互为不等于0的相反数,n 为正整数,你认为正确的是( )A.x n 、y n 一定是互为相反数B.(x 1)n 、(y1)n 一定是互为相反数C.x 2n 、y 2n 一定是互为相反数D.x 2n -1、-y 2n -1一定相等二、填空题:13、(-2x+y )(-2x -y )=_________. 14、(-3x 2+2y 2)(_________)=9x 4-4y 4. 15、19×21×(202+1)=________.16、两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是_________.17、计算:(a+1)(a -1)=_________.18、若a 2+b 2-2a+2b+2=0,则a 2010+b 2011=_________.19、一个长方形的长为(2a+3b),宽为(2a -3b),则长方形的面积为________. 20、5-(a -b)2的最大值是________。

2021-2022学年人教版八年级数学上册《14.2乘法公式》同步达标训练(附答案)1.下列各式,能用平方差公式计算的是()A.(2a+b)(2b﹣a)B.(﹣a﹣2b)(﹣a+2b)C.(2a﹣3b)(﹣2a+3b)D.()(﹣)2.下列各式中,不能用平方差公式计算的是()A.(﹣2x+y)(2x+y)B.(x2﹣y2)(x2+y2)C.(x+y)(﹣y+x)D.(﹣x+y)(x﹣y)3.如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是()A.a2+b2=(a+b)(a﹣b)B.(a﹣b)2=a2﹣2ab+b2C.(a+b)2=a2+2ab+b2D.a2﹣b2=(a+b)(a﹣b)4.若实数m,n满足(m2+2n2+5)(m2+2n2﹣5)=0,则m2+2n2的值为()A.5B.2.5C.2.5或﹣5D.5或﹣55.某同学在计算3(4+1)(42+1)时,把3写成(4﹣1)后,发现可以连续运用两数和乘以这两数差公式计算:3(4+1)(42+1)=(4﹣1)(4+1)(42+1)=(42﹣1)(42+1)=162﹣1=255.请借鉴该同学的经验,计算:(1+)(1+)+=()A.2﹣B.2+C.1D.26.若x2﹣6x+k是完全平方式,则k的值是()A.±9B.9C.±12D.127.若多项式4x2﹣mx+9是完全平方式,则m的值是()A.6B.12C.±12D.±68.用4块完全相同的长方形拼成如图所示的正方形,用不同的方法计算图中阴影部分的面积,可得到一个关于a,b的等式为()A.4a(a+b)=4a2+4ab B.(a+b)(a﹣b)=a2﹣b2C.(a+b)2=a2+2ab+b2D.(a+b)2﹣(a﹣b)2=4ab9.若(2m+5)(2m﹣5)=15,则m2=.10.已知x2﹣y2=21,x﹣y=3,则x+y=.11.已知m﹣n=3,则m2﹣n2﹣6n的值.12.观察下列各式:(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,…根据规律可得:(x﹣1)(x2021+x2020+…+x+1)=.13.计算:20212﹣2021×4040+20202=.14.若(x﹣y)2=5,xy=1,则(x+y)2=.15.已知:a+b=5,(a﹣b)2=13,则ab的值是.16.已知m+n=3,则m2﹣n2+6n=.17.如图,两个正方形边长分别为a和b,如果a+b=7,ab=6,则阴影部分的面积为.18.如图,长方形ABCD的周长为12,面积为3,分别以BC,CD为边作正方形,则图中阴影部分的面积为.19.如图,两个正方形边长分别为a、b,如果a2+b2=300,ab=12,则阴影部分的面积为.20.计算:(1)20092﹣2010×2008;(2)(x﹣y)(4x+3y)﹣(2x+y)(2x﹣y).21.用简便方法计算.(1)100.5×99.5.(2)2018×2020﹣20192.22.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是.(请选择正确的一个)A.a2﹣2ab+b2=(a﹣b)2B.a2+ab=a(a+b)C.a2﹣b2=(a+b)(a﹣b)(2)运用你从(1)中选出的等式,完成下列各题:①已知9x2﹣4y2=18,3x﹣2y=3.求3x+2y的值.②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).23.(1)已知(a+b)2=6,(a﹣b)2=2,求a2+b2与ab的值;(2)已知a+b=8,a2b2=9,求a2+b2的值.24.【问题解决】(1)若a+b=4,ab=2,求a2+b2的值;【类比探究】(2)若x+y=8,x2+y2=40,求xy的值;【拓展延伸】(3)如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形ACDE和BCFG,已知AB=10,两正方形的面积和S1+S2=60,求图中阴影部分的面积.25.某同学用如图所示不同颜色的正方形与长方形拼成了一个如图所示的正方形.(1)①请用两种不同的方法求图中阴影总分的面积.方法1:;方法2:.②以上结果可以验证的乘法公式是.(2)根据上面的结论计算:①已知m+n=5,m2+n2=11,求mn的值.②已知(2019﹣m)(2020﹣m)=1010,求(2020﹣m)2+(m﹣2019)2的值.参考答案1.解:A.既没有相同项,也没有相反项,不能用平方差公式进行计算,故本选项不符合题意;B.原式=﹣(2b+a)(2b﹣a),符合平方差公式,故本选项符合题意;C.原式=﹣(2a﹣3b)(2a﹣3b),只有相同项,没有相反项,不符合平方差公式,故本选项不符合题意;D.原式=﹣()()只有相同项,没有相反项,不符合平方差公式,故本选项不符合题意;故选:B.2.解:A.(﹣2x+y)(2x+y),此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;B.(x2﹣y2)(x2+y2),此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;C.(x+y)(﹣y+x),此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;D.(﹣x+y)(x﹣y),两项均互为相反数,不符合平方差公式的特征,不能用平方差公式计算,故此选项符合题意.故选:D.3.解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),故选:D.4.解:∵实数m,n满足(m2+2n2+5)(m2+2n2﹣5)=0,∴实数m,n满足(m2+2n2)2﹣52=0,∴(m2+2n2)2=52,∴m2+2n2=5,或m2+2n2=﹣5(舍去).故选:A.5.解:原式=2×(1﹣)(1+)(1+)+=2×(1﹣)(1+)+=2×(1﹣)+=2﹣+=2.故选:D.6.解:∵x2﹣6x+k是完全平方式,∴k=32=9.故选:B.7.解:∵多项式4x2﹣mx+9是一个完全平方式,∴4x2﹣mx+9=(2x﹣3)2或4x2﹣mx+9=(2x+3)2,即4x2﹣mx+9=x2﹣12x+9或4x2﹣mx+9=x2+12x+9,∴m=12或m=﹣12,故选:C.8.解:∵图形中大正方形的面积为(a+b)2,中间空白正方形的面积为(a﹣b)2,∴图中阴影部分的面积为(a+b)2﹣(a﹣b)2,又∵图中阴影部分的面积还可表示为4ab,∴(a+b)2﹣(a﹣b)2=4ab,故选:D.9.解:由(2m+5)(2m﹣5)=15,得4m2﹣25=15.解得m2=10.故答案是:10.10.解:因为x2﹣y2=(x﹣y)(x+y)=21,x﹣y=3,所以x+y==7.故答案为:7.11.解:∵m﹣n=﹣3,∴原式=(m﹣n)(m+n)﹣6n=3(m+n)﹣6n=3m﹣3n=3(m﹣n)=9..故答案为:9.12.解:观察每一个等式左边的代数式与右边的代数式,得(x﹣1)(x2021+x2020+…+x+1)=x2022﹣1.故答案为:x2022﹣1.13.解:20212﹣2021×4040+20202=20212﹣2×2021×2020+20202=(2021﹣2020)2=12=1.14.解:∵(x﹣y)2=5,xy=1,∴(x+y)2=(x﹣y)2+4xy=5+4×1=9.故答案为9.15.解:∵a+b=5,(a﹣b)2=13,∴a2+b2+2ab=25①,a2+b2﹣2ab=13②,则①﹣②可得:4ab=12,所以ab=3.故答案为:3.16.解:因为m+n=3,所以m2﹣n2+6n=(m+n)(m﹣n)+6n=3(m﹣n)+6n=3m﹣3n+6n=3(m+n)=3×3=9,故答案为:9.17.解:根据题意得:S阴影=a2﹣b(a﹣b)=a2﹣ab+b2;当a+b=7,ab=6时,S阴影=(a2﹣ab+b2)=[(a+b)2﹣3ab]=(72﹣3×6)=.故答案为:.18.解:设长方形ABCD的长为x,宽为y,由题意得:,∴x+y=6,∴(x+y)2=36,∴x2+2xy+y2=36,∴x2+y2=36﹣2xy==36﹣6=30,∴图中阴影部分的面积为30,故答案为:30.19.解:∵a2+b2=300,ab=12,∴===144.故答案为:144.20.解:(1)原式=20092﹣(2009+1)×(2009﹣1)=20092﹣20092+1=1;(2)原式=4x2+3xy﹣4xy﹣3y2﹣(4x2﹣y2)=4x2+3xy﹣4xy﹣3y2﹣4x2+y2=﹣2y2﹣xy.21.解:(1)原式=(100+0.5)×(100﹣0.5)=1002﹣0.52=10000﹣0.25=9999.75;(2)2018×2020﹣20192=(2019﹣1)(2019+1)﹣20192=20192﹣1﹣20192=﹣1.22.解:(1)图1阴影部分面积为:a2﹣b2,图2阴影部分面积为:(a+b)(a﹣b),∵图1阴影部分面积=图2阴影部分面积,∴a2﹣b2=(a+b)(a﹣b).(2)①∵9x2﹣4y2=18,∴(3x+2y)(3x﹣2y)=18,∵3x﹣2y=3,∴3x+2y=6,②(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣)=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)……(1﹣)(1+)===.23.解:(1)∵(a+b)2=6,(a﹣b)2=2,∴a2+2ab+b2=6①,a2﹣2ab+b2=2②,∴①+②得:a2+2ab+b2+a2﹣2ab+b2=8,则a2+b2=4;①﹣②得:4ab=4,则ab=1;(2)∵a+b=8,a2b2=9,∴(a+b)2=64,ab=±3,∴a2+2ab+b2=64,∴a2+b2=64﹣2ab=64﹣2×3=58,或a2+b2=64﹣2ab=64﹣2×(﹣3)=70,即a2+b2的值是58或70.24.解:(1)因为a+b=4,ab=2,所以(a+b)2=16,2ab=4,所以a2+b2+2ab=16,所以a2+b2=16﹣4=12;(2)因为x+y=8,所以(x+y)2=64,所以x2+y2+2xy=64,因为x2+y2=40,所以2xy=64﹣40=24,xy=12;(3)设AC=m,BC=n,则S1=m2,S2=n2,S1+S2=m2+n2=60,因为AB=10,即m+n=10,所以(m+n)2=100,m2+n2+2mn=100,2mn=100﹣60=40,mn=20,所以S△BCD=mn==10.故图中阴影部分的面积为10.25.解(1)①由题意,得两种不同的方法求图中阴影总分的面积为a2+b2,(a+b)2﹣2ab,故答案为:a2+b2,(a+b)2﹣2ab,②由①题结果可得(a+b)2=a2+2ab+b2;(2)①利用(1)题中②的结果(a+b)2=a2+2ab+b2,可得ab=,∴当m+n=5,m2+n2=11时,mn==7.②由(1)题中②的结果(a+b)2=a2+2ab+b2,可得a2+b2=(a+b)2﹣2ab,∵(2019﹣m)(2020﹣m)=1010,∴(2020﹣m)(m﹣2019)=﹣1010,∵(2020﹣m)+(m﹣2019)=1,∴(2020﹣m)2+(m﹣1019)2=(2020﹣m+m﹣2019)2﹣2(2020﹣m)(m﹣2019)=12﹣2(﹣1010)=1+2020=2021.。

2022-2023学年人教版八年级数学上册《14.2乘法公式》同步作业题(附答案)一.选择题1.下列能用平方差公式计算的是()A.(﹣x+y)(x﹣y)B.(﹣x+y)(x+y)C.(x+2)(x﹣1)D.(2x+3)(3x﹣2)2.若x2+2(m﹣5)x+16是完全平方式,则m的值是()A.5B.9C.9或1D.5或13.下列各式正确的是()A.(2a﹣1)2=4a2﹣1B.(x+)2=x2+x+C.(3m+n)2=9m2+n2D.(﹣x﹣1)2=x2﹣2x+14.若a+2b=7,ab=6,则(a﹣2b)2的值是()A.3B.2C.1D.05.若n满足关系式(n﹣2020)2+(2021﹣n)2=3,则代数式(n﹣2020)(2021﹣n)=()A.﹣1B.0C.D.16.如图,有两个正方形A,B,现将B放置在A的内部得到图甲,将A、B并列放置,以正方形A与正方形B的边长之和为新的边长构造正方形得到图乙,若图甲和图乙中阴影部分的面积分别为1和8,则正方形A、B的面积之和为()A.8B.9C.10D.12二.填空题7.若,,则(m+n)2=.8.已知(m﹣2020)2+(2022﹣m)2=34,则m﹣2021的值为.9.已知a2+b2=25,a+b=7,则ab=.10.已知x+y=6,xy=3,则x2+y2的值是.11.若实数x、y满足x﹣3=y,则代数式2x2﹣4xy+2y2的值为.12.若x2﹣2(a﹣3)x+16是关于x的完全平方式,则a的值是.13.若a+b=3,ab=1,则a﹣b=.14.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长宽分别为2和1的长方形,现用甲类纸片1张,乙类纸片4张,丙类纸片若干张拼成一个新的大正方形,则至少需要丙类纸片张.15.现有如图①的小长方形纸片若干块,已知小长方形的长为a(cm),宽为b(cm).用3个如图②的完全相同的图形和8个如图①的小长方形,拼成如图③的大长方形,则图③中阴影部分面积与整个图形的面积之比为.16.如图,两个正方形的边长分别为a,b(a>b),若a+b=10,ab=6,则阴影部分的面积为.三.解答题17.已知有理数x,y满足x+y=,xy=﹣3.(1)求(x+1)(y+1)的值;(2)求x2+y2的值.18.计算:(3x+2y)(3x﹣2y)﹣3x(x+2y).19.化简(a+3)2﹣(a﹣3)(a+3).20.2023×2021﹣20222.21.(﹣2x+3y﹣1)(﹣2x﹣3y+1).22.(a﹣4)(a+4)﹣2(a﹣1)(2a+2).23.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2).(1)设图1中阴影部分的面积为S₁,图2中阴影部分的面积为S₂,请用含a.b的式子表示:S₁=,S₂=;(不必化简)(2)以上结果可以验证的乘法公式是.(3)利用(2)中得到的公式,计算;20202﹣2019×2021.24.前面学习中,一些乘法公式可以通过几何图形来验证,请结合下列两组图形回答问题:图①说明:左侧图形中阴影部分由右侧阴影部分分割后拼接而成;图②说明:边长为(a+b)的正方形的面积分割成如图所示的四部分.(1)请结合图①和图②分别写出学过的两个乘法公式:图①:;图②:.(2)请利用上面的乘法公式计算:①1002﹣99×101;②(60)2.25.若x满足(x﹣4)(x﹣9)=6,求(x﹣4)2+(x﹣9)2的值.阅读下面求解的方法:解:设(x﹣4)=a,(x﹣9)=b,则ab=(x﹣4)(x﹣9)=6,a﹣b=(x﹣4)﹣(x ﹣9)=5∴(x﹣4)2+(x﹣9)2=a2+b2=(a﹣b)2+2ab=52+2×6=37.请仿照上面的方法求解下面的问题:(1)若x满足(x﹣2)(x﹣5)=10,求(x﹣2)2+(x﹣5)2的值;(2)如图,正方形ABCD中,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF为边作正方形,若AD=x,则①DE=,DF=(用含x的代数式表示);②直接写出图中阴影部分的面积.参考答案一.选择题1.解:A、(﹣x+y)(x﹣y),两项都互为相反数,不符合平方差公式;B(﹣x+y)(x+y),两项中,有一项完全相同,另一项互为相反数,符合平方差公式;C、(x+2)(x﹣1)中有一项完全相同,但另一项不是互为相反数,不符合平方差公式;D、(2x+3)(3x﹣2)中各项不同,不符合平方差公式.故选:B.2.解:∵x2+2(m﹣5)x+16是完全平方式,∴m﹣5=±4,解得:m=9或1,则m的值是9或1.故选:C.3.解:(2a﹣1)2=4a2﹣4a+1,选项A错误;(x+)2=x2+x+,B选项正确;(3m+n)2=9m+6mn+n2,C选项错误;(﹣x﹣1)2=x2+2x+1,选项D错误.故选:B.4.解:(a﹣2b)2=a2+4b2﹣4ab=a2+4b2+4ab﹣8ab=(a+2b)2﹣8ab,∵a+2b=7,ab=6,∴原式=72﹣8×6=49﹣48=1.故选:C.5.解:∵(n﹣2020)2+(2021﹣n)2=3,∴(n﹣2020)2+2(n﹣2020)(2021﹣n)+(2021﹣n)2﹣2(n﹣2020)(2021﹣n)=﹣3,∴1﹣2(n﹣2020)(2021﹣n)=3,∴﹣2(n﹣2020)(2021﹣n)=2,∴(n﹣2020)(2021﹣n)=﹣1,故选:A.6.解:设大小正方形边长分别为a、b,S阴1=(a﹣b)2=1,即a2+b2﹣2ab=1,S阴2=(a+b)2﹣a2﹣b2=8,得:ab=4.∴a2+b2﹣2×4=1,∴a2+b2=9.故选:B.二.填空题7.解:∵m2﹣n2=(m+n)(m﹣n),而,,∴2(m+n)=12,∴m+n=6,(m+n)2=62=36.故答案为36.8.解:∵(m﹣2020)2+(m﹣2022)2=34,∴[(m﹣2021)+1]2+[(m﹣2021)﹣1]2=34,∴(m﹣2021)2+2(m﹣2021)+1+(m﹣2021)2﹣2(m﹣2021)+1=34,∴2(m﹣2021)2=32,∴(m﹣2021)2=16,∴m﹣2021=±4.故答案是:±4.9.解:∵a2+b2=25,a+b=7,∴(a+b)2=a2+2ab+b2=72=49,∴ab=12;故答案是:12.10.解:∵x+y=6,xy=3,∴x2+y2=(x+y)2﹣2xy=36﹣2×3=30.故答案为:30.11.解:由x﹣3=y可得x﹣y=3,∴2x2﹣4xy+2y2=2(x2﹣2xy+y2)=2(x﹣y)2=2×32=2×9=18.故答案为:18.12.解:∵x2﹣2(a﹣3)x+16是一个完全平方式,∴﹣2a+6=±8,∴a=7或﹣1.故答案为7或﹣1.13.解:∵a+b=3,ab=1,∴(a﹣b)2=(a+b)2﹣4ab=32﹣4×1=5,∴a﹣b=,故答案为:.14.解:甲类纸片1张,乙类纸片4张,总面积是4+4=8,大于8的完全平方数依次是9,16,25…,而丙的面积是2,因而不可能是9;当总面积是16时,取的丙纸片的总面积是8,因而是4张.因而应至少取丙类纸片4张才能用它们拼成一个新的正方形.故答案为:4.15.解:∵阴影面积为3(a﹣b)2,整个图形的面积为:4a(a+3b),∴阴影部分面积与整个图形的面积之比为,由题意3a+3b=4a,∴a=3b,∴==,故答案为:.16.解:S阴影=S大正方形+S小正方形﹣S△ABD﹣S△BEF =a2+b2﹣a2﹣b(a+b)=a2+b2﹣ab=(a2+b2+2ab)﹣ab=(a+b)2﹣ab∵a+b=10,ab=6;∴原式=×102﹣×6=×100﹣9=41故答案为:41.三.解答题17.解:(1)(x+1)(y+1)=xy+(x+y)+1=﹣3++1=﹣1;(2)x2+y2=(x+y)2﹣2xy=+6=6.18.解:(3x+2y)(3x﹣2y)﹣3x(x+2y)=9x2﹣4y2﹣3x2﹣6xy=6x2﹣6xy﹣4y2.19.解:原式=a2+6a+9﹣(a2﹣9)=a2+6a+9﹣a2+9=6a+18.20.解:2023×2021﹣20222=(2022+1)×(2022﹣1)﹣20222=20222﹣1﹣20222=-121.解:(﹣2x+3y﹣1)(﹣2x﹣3y+1)=[(﹣2x)+(3y﹣1)][(﹣2x)﹣(3y﹣1)]=(﹣2x)2﹣(3y﹣1)2=4x2﹣9y2+6y﹣1.22.解:(a﹣4)(a+4)﹣2(a﹣1)(2a+2)=a2﹣42﹣4(a﹣1)(a+1)=a2﹣16﹣4(a2﹣1)=a2﹣16﹣4a2+4=﹣3a2﹣12.23.解:(1)根据图形以及正方形和长方形的面积计算公式可得:S₁=a2﹣b2,S₂=(a+b)(a﹣b)故答案为:a2﹣b2,(a+b)(a﹣b);(2)以上结果可以验证的乘法公式是a2﹣b2=(a+b)(a﹣b).故答案为:(a+b)(a﹣b)=a2﹣b2.(3)20202﹣2019×2021=20202﹣(2020﹣1)×(2020+1)=20202﹣(20202﹣1)=20202﹣20202+1=1.24.解:(1)由图①可得,(a+b)(a﹣b)=a2﹣b2;由图②可得,(a+b)2=a2+2ab+b2;故答案为:(a+b)(a﹣b)=a2﹣b2,(a+b)2=a2+2ab+b2;(2)①1002﹣99×101=1002﹣(100﹣1)×(100+1)=1002﹣(1002﹣1)=1002﹣1002+1=1;②(60)2=(60+)2=3600+2+=3602.25.解:(1)设(x﹣2)=a,(x﹣5)=b,则ab=(x﹣2)(x﹣5)=10,a﹣b=(x﹣2)﹣(x﹣5)=3,∴(x﹣2)2+(x﹣5)2=a2+b2=(a﹣b)2+2ab=32+2×10=29;(2)①∵AE=1,CF=3,正方形ABCD边长为x,∴DE=x﹣1,DF=x﹣3.故答案为:x﹣1,x﹣3;②∵长方形EMFD的面积是15,∴(x﹣1)(x﹣3)=15,设x﹣1=a,x﹣3=b,则ab=15,a﹣b=2,∴(x﹣1+x﹣3)²=(a+b)²=(a﹣b)²+4ab=2²+4×15=64,∵a≥0,b≥0,∴x﹣1+x﹣3=a+b=8,∴阴影部分面积为(x﹣1)2﹣(x﹣3)2=a²﹣b²=(a+b)(a﹣b)=16.。

2022-2023学年人教版八年级数学上册《14.2乘法公式》同步练习题(附答案)一.选择题1.下列算式能用平方差公式计算的是()A.(2a+b)(2b﹣a)B.C.(3x﹣y)(﹣3x+y)D.(﹣m﹣n)(﹣m+n)2.下列各式计算结果为16y2﹣x2的是()A.(4y﹣x)(﹣4y﹣x)B.(﹣4y﹣x)(﹣4y+x)C.(4y+x)(﹣4y+x)D.(x+4y)(﹣x﹣4y)3.(5a2+4b2)()=25a4﹣16b4,括号内应填()A.5a2+4b2B.5a2﹣4b2C.﹣5a2﹣4b2D.﹣5a2+4b2 4.已知:a+b=5,a﹣b=1,则a2﹣b2=()A.5B.4C.3D.25.若M(3a﹣b2)=b4﹣9a2,那么代数式M应是()A.﹣3a+b2B.3a+b2C.3a﹣b2D.﹣3a﹣b26.将形状大小完全相同四个小正方形,按照如图所示的两种方式放置于两个边长不相等的大正方形中,根据两个图形中阴影部分的面积关系,得到的等式是()A.(m+n)(m﹣n))=m2﹣n2B.(m+n)2=m2+2mn+n2C.(m+n)2﹣(m﹣n)2=4mm D.(m﹣n)2=m2﹣2mn+n27.计算(﹣2a+3b)2,结果是()A.2a2+12ab+3b2B.2a2﹣12ab+3b2C.4a2+12ab+9b2D.4a2﹣12ab+9b28.已知(3x+a)2=9x2+bx+4,则b的值为()A.4B.±6C.12D.±129.已知(a+b)2=28,(a﹣b)2=12,则a2+b2的值为()A.8B.16C.20D.4010.用4个长为a,宽为b的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是()A.(a+b)2=a2+2ab+b2B.(a﹣b)2=a2﹣2ab+b2C.(a+b)(a﹣b)=a2﹣b2D.(a+b)2﹣(a﹣b)2=4ab二.填空题11.若a﹣b=﹣3,a2﹣b2=12,则a+b=.12.若m2﹣n2=6,且m﹣n=2,则m+n的值为.13.计算:(2x+1)(2x﹣1)(4x2+1)=.14.=.15.若(x2+y2﹣1)2=25,则x2+y2=.16.9m2﹣5m+1+=(3m﹣1)2.17.若x2+8x﹣m可以写成一个多项式的平方的形式,则m=.18.若x2+(m﹣2)x+16是一个完全平方式,则m的值是.三.解答题19.计算:(2x﹣3)2﹣6x(x﹣2).20.计算:(a+2b)(a﹣2b)+(3a﹣2b)2.21.请你参考黑板中老师的讲解,用乘法公式进行简便计算:利用乘法公式有时可以进行简便计算.例1:1012=(100+1)2=1002+2×100×1+1=10201;例2:17×23=(20﹣3)(20+3)=202﹣32=391.(1)9992;(2)20222﹣2021×2023.22.以下小明化简代数式(a+b)2﹣2(a+b)(a﹣b)+(a﹣b)2的过程:解:原式=a2+b2﹣2(a2﹣b2)+a2﹣b2①=a2+b2﹣2a2﹣2b2+a2﹣b2②=﹣2b2③(1)解答过程中哪几步错误?原因是什么?(2)写出正确解答过程.23.已知x2+y2=34,x+y=2,求xy和x﹣y的值.24.已知2m2+5m﹣1=0,求代数式(m+3)2+m(m﹣1)的值.25.已知x+y=3,且(x+3)(y+3)=20.(1)求xy的值;(2)求x2+5xy+y2的值;(3)求x﹣y的值.参考答案一.选择题1.解:(2a+b)(2b﹣a)=﹣2a2+3ab+2b2不能用平方差公式,故A选项不符合题意;=不能用平方差公式,故B选项不符合题意;(3x﹣y)(﹣3x+y)=﹣9x2+6xy﹣y2,不能用平方差公式,故C选项不符合题意;(﹣m﹣n)(﹣m+n)=m2﹣n2,能用平方差公式,故D选项符合题意,故选:D.2.解:(﹣4y﹣x)(﹣4y+x)=16y2﹣x2.故选:B.3.解:∵(5a2+4b2)(5a2﹣4b2)=25a4﹣16b4,∴括号内应填5a2﹣4b2,故选:B.4.解:∵a+b=5,a﹣b=1,∴a2﹣b2=(a+b)(a﹣b)=5×1=5,故选:A.5.解:M===﹣b2﹣3a,故选:D.6.解:图1中“大正方形”的边长为m﹣n,因此面积为(m﹣n)2,图2中阴影部分的面积为m2﹣2mn+n2,所以有(m﹣n)2=m2﹣2mn+n2,故选:D.7.解:(﹣2a+3b)2=(﹣2a)2+2×(﹣2a)×3b+(3b)2=4a2﹣12ab+9b2,故选:D.8.解:∵(3x±2)2=9x2±12x+4,∴b=±12,故选:D.9.解:∵(a+b)2=28,(a﹣b)2=12,∴a2+b2+2ab=28①,a2+b2﹣2ab=12②,∴①+②得:2(a2+b2)=40,∴a2+b2=20,故选:C.10.解:∵此题阴影部分面积可表示为:(a+b)2﹣(a﹣b)2和4ab,∴可得等式(a+b)2﹣(a﹣b)2=4ab,故选:D.二.填空题11.解:由平方差公式(a+b)(a﹣b)=a2﹣b2,可得a+b=(a2﹣b2)÷(a﹣b)=12÷(﹣3)=﹣4,故答案为:﹣4.12.解:∵m2﹣n2=6,且m﹣n=2,∴(m+n)(m﹣n)=2(m+n)=6.∴m+n=3.故答案为:3.13.解:(2x+1)(2x﹣1)(4x2+1)=(4x2﹣1)(4x2+1)=16x4﹣1.故答案为:16x4﹣1.14.解:==﹣,故答案为:﹣.15.解:∵(x2+y2﹣1)2=25,∴x2+y2﹣1=±5,∴x2+y2=6或﹣4,又∵x2+y2≥0,所以x2+y2=6,故答案为:6.16.解:(3m﹣1)2=9m2﹣6m+1,9m2﹣6m+1﹣(9m2﹣5m+1)=﹣m,故答案为:(﹣m).17.解:∵x2+8x﹣m可以写成一个多项式的平方的形式,∴x2+8x﹣m=x2+2•x•4+42,∴﹣m=42,∴m=﹣16,故答案为:﹣16.18.解:∵x2+(m﹣2)x+16是一个完全平方式∴m﹣2=±8,解得:m=10或﹣6,故答案为:10或﹣6.三.解答题19.解:原式=4x2﹣12x+9﹣(6x2﹣12x)=4x2﹣12x+9﹣6x2+12x=﹣2x2+9.20.解:原式=a2﹣4b2+9a2﹣12ab+4b2=10a2﹣12ab.21.解:(1)原式=(1000﹣1)2=10002﹣2×1000×1+1=1000000﹣2000+1=998001;(2)20222﹣(2022﹣1)×(2022+1)=20222﹣20222﹣+1=1.22.解:(1)解答过程中第①步错,完全平方公式运用出错;第②步错,去括号出错;(2)原式=a2+2ab+b2﹣2(a2﹣b2)+a2﹣2ab+b2=a2+2ab+b2﹣2a2+2b2+a2﹣2ab+b2=4b2.23.解:∵x2+y2=34,x+y=2,x2+y2=(x+y)2﹣2xy,∴34=22﹣2xy,∴xy=﹣15,∴(x﹣y)2=x2﹣2xy+y2=34﹣2×(﹣15)=64,∴x﹣y=±8.24.解:∵2m2+5m﹣1=0,∴2m2+5m=1,∴(m+3)2+m(m﹣1)=m2+6m+9+m2﹣5m=2m2﹣5m+9=1+9=10.25.解:(1)∵(x+3)(y+3)=xy+3(x+y)+9=20,x+y=3,∴xy=2;(2)x2+5xy+y2=(x+y)2+3xy=9+6=15;(3)∵(x﹣y)2=x2+y2﹣2xy=(x+y)2﹣4xy,∴(x﹣y)2=9﹣8=1,∴x﹣y=±1.。

2022-2023学年人教版八年级数学上册《14.2乘法公式》同步练习题(附答案)一.选择题1.下列各式计算正确的是()A.(a+b)2=a2+b2B.(a﹣b)2=a2﹣b2C.(x﹣y)2=x2﹣2xy+y2D.(x+2)(x﹣1)=x2﹣x﹣22.下列各式正确的是()A.(2a﹣1)2=4a2﹣1B.(x+)2=x2+x+C.(3m+n)2=9m2+n2D.(﹣x﹣1)2=x2﹣2x+13.下列等式成立的是()A.(2+x)(x﹣2)=x2﹣4B.(2x﹣y)(﹣2x+y)=4x2﹣y2C.(3m+2n)(3m﹣2n)=9m3﹣2n2D.(a+b)(﹣a﹣b)=a2﹣b24.若等式(3x+5)2(3x﹣5)2=81x4﹣mx2+n2成立,则()A.m=﹣30,n=5B.m=﹣30,n=﹣5或5C.m=﹣450,n=25或﹣25D.m=450,n=25或﹣255.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22﹣02,12=42﹣22,20=62﹣42,因此4,12,20都是“神秘数”,则下面哪个数是“神秘数”()A.56B.60C.62D.886.若(3b+a)()=9b2﹣a2,则括号内应填的代数式是()A.﹣a﹣3b B.a+3b C.﹣3b+a D.3b﹣a7.计算20212﹣2020×2022的结果是()A.1B.﹣1C.0D.2×20212﹣1 8.式子(2+1)(22+1)(24+1)(28+1)…(21024+1)+1化简的结果为()A.21024B.21024+1C.22048D.22048+19.如图1,从边长为a的大正方形纸片中挖去一个边长为b的小正方形纸片后,将其沿实线裁成两个相同的直角梯形,然后拼成一个等腰梯形(如图2),则通过计算图形阴影部分的面积,可以验证成立的公式是()A.(a﹣b)2=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)10.如图,从边长为(a+5)cm的正方形纸片中剪去一个边长为(a+2)cm的小正方形,剩余部分沿虚线剪拼成一个矩形(不重叠无缝隙),则矩形的面积为()cm2.A.a2+5a B.6a+21C.6a+14D.3a+2111.图1,是一个长为2m、宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2形式拼成一个正方形,那么中间阴影部分的面积为()A.mn B.m2﹣n2C.(m﹣n)2D.(m+n)2二.填空题12.设N=2(1﹣)(1﹣)(1﹣)……(1﹣)(1﹣),则N的值为.13.已知x2﹣y2=﹣5,则代数式(x+y)3•(x﹣y)3的值为.14.若a=20220,b=2021×2023﹣20222,c=82022×(﹣0.125)2023,则a,b,c的大小关系是(用“>”连接).15.已知4x2+mxy+16y2是完全平方式,则m=.16.若多项式4x2﹣(k﹣1)x+9可以写成一个完全平方式,则k=.三.解答题17.计算:4(x+1)2﹣(2x+5)(2x﹣5)18.计算:.19.已知,求值:(1)(2).20.对于任意四个实数a,b,c,d,可以组成两个实数对(a,b)与(c,d).我们规定:(a,b)⊗(c,d)=a2+d2﹣bc.例如:(1,2)⊗(3,4)=12+42﹣2×3=11.(1)若(3x,﹣3x)⊗(ky,y)是一个完全平方式,则常数k的值为;(2)若x+y=6,且(2x+y,x2+y2)⊗(2,x﹣2y)=60,求xy的值.21.数学活动课上,刘老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形并用A种纸片一张,B 种纸片一张,C种纸片两张拼成如图2的大正方形.由图2,可得出三个代数式:(a+b)2,a2+b2,ab之间的等量关系;(1)根据上述方法,要拼出一个面积为(a+2b)(a+b)的矩形,需要A卡片1张,B卡片2张,C卡片张.(2)根据得出的等量关系,解决如下问题:①已知:a+b=6,a2+b2=14,求ab的值;②已知(x﹣2020)2+(x﹣2022)2=10,求(x﹣2021)2的值.22.乘法公式的探究及应用.(1)如图1,可以求出阴影部分的面积是(写成两数平方差的形式);(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是,长是,面积是;(写成多项式乘法的形式)(3)比较左、右两图的阴影部分面积,可以得到乘法公式;(用式子表达)(4)运用你所得到的公式,计算下列各题:①20212﹣2020×2022;②(2m+n+p)(2m+n﹣p).参考答案一.选择题1.解:A、(a+b)2=a2+2ab+b2,故本选项不符合题意;B、(a﹣b)2=a2﹣2ab+b2,故本选项不符合题意;C、(x﹣y)2=x2﹣2xy+y2,故本选项符合题意;D、(x+2)(x﹣1)=x2+x﹣2,故本选项不符合题意.故选:C.2.解:(2a﹣1)2=4a2﹣4a+1,选项A错误;(x+)2=x2+x+,B选项正确;(3m+n)2=9m+6mn+n2,C选项错误;(﹣x﹣1)2=x2+2x+1,选项D错误.故选:B.3.解:(2+x)(x﹣2)=x2﹣4,故A成立,符合题意;(2x﹣y)(﹣2x+y)=﹣4x2+4xy﹣y2,故B不成立,不符合题意;(3m+2n)(3m﹣2n)=9m2﹣4n2,故C不成立,不符合题意;(a+b)(﹣a﹣b)=﹣a2﹣2ab﹣b2,故D不成立,不符合题意;故选:A.4.解:由于(3x+5)2(3x﹣5)2=81x4﹣mx2+n2,即[(3x+5)(3x﹣5)]2=81x4﹣mx2+n2,也就是(9x2﹣25)2=81x4﹣mx2+n2,所以81x4﹣450x2+625=81x4﹣mx2+n2,即m=450,n=±25,故选:D.5.解:∵60=162﹣142,∴60是“神秘数”,故选:B.6.解:∵9b2﹣a2=(3b+a)(3b﹣a),故选:D.7.解:原式=20212﹣(2021﹣1)×(2021+1)=20212﹣(20212﹣1)=20212﹣20212+1=1.故选:A.8.解:设S=(2+1)(22+1)(24+1)(28+1)…(21024+1)∴(2﹣1)S=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(21024+1)=(22﹣1)(22+1)(24+1)(28+1)…(21024+1)=(24﹣1)(24+1)(28+1)…(21024+1)=(21024﹣1)(21024+1)=22048﹣1,∴(2+1)(22+1)(24+1)(28+1)…(21024+1)+1=S+1=22048﹣1+1=22048.故选:C.9.解:∵图形中阴影部分的面积可表示为a2﹣b2或=(a+b)(a﹣b),∴a2﹣b2=(a+b)(a﹣b),故选:D.10.解:拼成矩形的长为a+2+a+5=2a+7,宽为a+5﹣a﹣2=3,所以面积为3(2a+7)=6a+21,故选:B.11.解:方法一:图2中四个长方形的面积的和=图1的长方形的面积=2m×2n=4mn,图2的大正方形的面积=(m+n)2,图2中阴影部分的面积=图2的大正方形的面积﹣图2中四个长方形的面积的和=(m+n)2﹣4mn=m2+2mn+n2﹣4mn=m2﹣2mn+n2=(m﹣n)2.方法二:图中阴影部分是正方形,且四个边长都是(m﹣n),∴阴影部分的面积=(m﹣n)2.故选:C.二.填空题12.解:N=2×(1﹣)×(1+)×(1﹣)×(1+)……(1﹣)×(1+)×(1﹣)×(1+)=2××××……××××=,故答案为:.13.解:∵x2﹣y2=﹣5,∴(x+y)(x﹣y)=﹣5,∴(x+y)3•(x﹣y)3=[(x+y)(x﹣y)]3=﹣125,故答案为:﹣125.14.解:a=20220=1,b=2021×2023﹣20222=(2022﹣1)(2022+1)﹣20222=20222﹣1﹣20222=﹣1,c=82022×(﹣0.125)2023=﹣0.125×(﹣0.125×8)2022=﹣0.125,∵﹣1<﹣0.125<1,∴b<c<a.故答案为:b<c<a.15.解:∵4x2+mxy+16y2是完全平方式,∴mxy=±2×2x×4y,∴m=±16.故答案为:±16.16.解:由于(2x±3)2=4x2±12x+9=4x2﹣(k﹣1)x+9,则﹣(k﹣1)=±12,解得:k=13或﹣11.故答案为:13或﹣11.三.解答题17.解:原式=4x2+8x+4﹣4x2+25=8x+29.18.解:原式=x2﹣xy+y2﹣(x2﹣y2)(4分)=﹣xy+y2.(2分)19.解:(1)∵x+﹣3=0,∴x+=3,∴=(x+)2﹣2=9﹣2=7,即=7;(2)由(1)知,=7,∴(x﹣)2=﹣2=7﹣2=5,∴x﹣=±.20.解:(1)(3x,﹣3x)⊗(ky,y)=(3x)2+y2﹣(﹣3x•ky)=9x2+3kxy+y2.∵(3x,﹣3x)⊗(ky,y)是一个完全平方式,∴3kxy=±6xy.∴k=±2.(2)∵(2x+y,x2+y2)⊗(2,x﹣2y)=60.(2x+y)2+(x﹣2y)2﹣2(x2+y2)=60.∴x2+y2=20.∵x+y=6.∴(x+y)2=36.∴x2+y2+2xy=36∴2xy=36﹣20=16.∴xy=8.21.解:(1)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片3张.故答案为:3.(2)①∵(a+b)2=a2+b2+2ab,∴2ab+14=36,∴ab=11;②(x﹣2020)2+(x﹣2022)2=10,∵[(x﹣2020)﹣(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2﹣2(x﹣2020)(x﹣2022),∴4=10﹣2(x﹣2020)(x﹣2022),∴2(x﹣2020)(x﹣2022)=6,∵[(x﹣2020)+(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2+2(x﹣2020)(x﹣2022),∴[2(x﹣2021)]2=10+6=16,即4(x﹣2021)2=16,∴(x﹣2021)2=4.22.解:(1)图1中阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,故答案为:a2﹣b2;(2)如图2,所拼成一个长方形,它的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b),故答案为:a﹣b,a+b,(a+b)(a﹣b);(3)由(1)(2)可得,(a+b)(a﹣b)=a2﹣b2,故答案为:(a+b)(a﹣b)=a2﹣b2;(4)①原式=20212﹣(2021﹣1)(2021+1)=20212﹣20212+1=1;②原式=[(2m+n)+p][(2m+n)﹣p]=(2m+n)2﹣p2=4m2+4mn+n2﹣p2.。
2022-2023学年人教版八年级数学上册《14.2乘法公式》同步自主达标测试题(附答案)一.选择题(共10小题,满分30分)1.下列各式中不能用平方差公式计算的是()A.B.(﹣2x+3y)(﹣3y﹣2x)C.(﹣2x+y)(﹣2x﹣y)D.(x﹣1)(﹣x+1)2.已知:a+b=5,a﹣b=1,则a2﹣b2=()A.5B.4C.3D.23.下列计算正确的是()A.x4+x2=x6B.x6÷x3=x2C.(5m﹣n)(﹣5m﹣n)=n2﹣25m2D.(﹣3xy)2=6x2y24.下列运算正确的是()A.2a2+a3=3a5B.a3•a2=a6C.(2a2)3=8a6D.(a+2)2=a2+45.已知x﹣y=3,xy=2,则(x+y)2的值等于()A.12B.13C.14D.176.已知a+b=2,求代数式a2﹣b2+4b的值为()A.0B.4C.5D.﹣77.用如图所示的几何图形的面积可以解释的代数恒等式是()A.(2a)2=4a2B.(a+b)2=a2+2ab+b2C.2a(a+b)=2a2+2ab D.2a(2a+b)=4a2+2ab8.若二次三项式x2+kx+4是一个完全平方式,则k的值是()A.4B.﹣4C.±2D.±49.如图将4个长、宽分别均为a和b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数式是()A.a2+2ab+b2=(a+b)2B.a2+2ab+b2=(a﹣b)2C.4ab=(a+b)2﹣(a﹣b)2D.(a+b)(a﹣b)=a2﹣b210.观察图形,用两种不同的方法计算大长方形面积,我们可以验证等式()A.(a+b)(a+2b)=a2+3ab+2b2B.(a+b)(2a+b)=2a2+3ab+b2C.(a+b)(a+2b)=2a2+3ab+b2D.(a+b)(2a+b)=a2+3ab+2b2二.填空题(共6小题,满分18分)11.计算982﹣99×97=.12.已知(a﹣b)2=13,ab=6,则a2+b2=.13.计算:(a﹣b+2c)2=.14.计算:(2b﹣3c+4)(3c﹣2b+4)﹣2(b﹣c)2=.15.计算:=.16.如果x﹣y=+1,y﹣z=﹣1,那么x2+y2+z2﹣xy﹣yz﹣zx=.三.解答题(共6小题,满分52分)17.已知(a+b)2=5,ab=﹣2,求代数式(a﹣b)2的值.18.计算:(x+y)2﹣2(x﹣y)(2x+y).19.用乘法公式进行计算:(1)20212﹣2022×2020;(2)112+13×66+392.(3)(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y).20.已知x+=3,求下列各式的值:(1)(x﹣)2;(2)x4+.21.如图1,从边长为a的大正方形中剪去一个边长为b的小正方形,把剩下的阴影部分拼成如图2所示的长方形.(1)上述操作能验证的公式是;(2)请应用这个公式完成下列各题:①已知4a2﹣b2=24,2a+b=6,则2a﹣b=;②计算:(1﹣)(1﹣)(1﹣)…(1﹣).22.如图1是一个长为4a,宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(1)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是.(2)根据(1)中的结论,若x+y=5,,求x﹣y的值.(3)变式应用:若(2020﹣m)2+(m﹣2021)2=7,求(2020﹣m)(m﹣2021).参考答案一.选择题(共10小题,满分30分)1.解:A、(+2b)(a﹣2b)=(a)2﹣(2b)2=﹣4b2,故能用平方差公式计算,故选项不符合题意;B、(﹣2x+3y)(﹣3y﹣2x)=(﹣2x)2﹣(3y)2=4x2﹣9y2,故能用平方差公式计算,故选项不符合题意;C、(﹣2x+y)(﹣2x﹣y)=(﹣2x)2﹣y2=4x2﹣y2,故能用平方差公式计算,故选项不符合题意;D、(x﹣1)(﹣x+1),不能用平方差公式计算,故选项符合题意.故选:D.2.解:∵a+b=5,a﹣b=1,∴a2﹣b2=(a+b)(a﹣b)=5×1=5,故选:A.3.解:A、x4与x2不是同类项,故不能合并,故A不符合题意.B、原式=x3,故B不符合题意.C、原式=﹣(5m﹣n)(5m+n)=﹣25m2+n2,故C符合题意.D、原式=9x2y2,故D不符合题意.故选:C.4.解:A.2a2和a3不能合并,故本选项不符合题意;B.a3•a2=a5,故本选项不符合题意;C.(2a2)3=8a6,故本选项符合题意;D.(a+2)2=a2+4a+4,故本选项不符合题意;故选:C.5.解:∵x﹣y=3,xy=2,∴(x+y)2=(x﹣y)2+4xy=9+8=17,故选:D.6.解:由a+b=2得:a=2﹣b,则a2﹣b2+4b=(2﹣b)2﹣b2+4b=4﹣4b+b2﹣b2+4b=4.故选:B.7.解:整体是长为2a,宽为a+b的长方形,因此面积为2a(a+b),这个长方形是由4个部分组成的,这4个部分的面积和为2a2+2ab,所以有2a(a+b)=2a2+2ab,故选:C.8.解:中间项为加上或减去x和2乘积的2倍,故k=±4.故选:D.9.解:由图可知,拼接后大正方形的边长为a+b,小正方形的边长为a﹣b,∴阴影部分的面积=(a+b)2﹣(a﹣b)2,∵阴影部分的面积是4个小长方形的面积和,∴阴影部分的面积=4ab,∴4ab=(a+b)2﹣(a﹣b)2,故选:C.10.解:整体是长为a+2b,宽为a+b的长方形,因此面积为(a+2b)(a+b),整体是由6个部分的面积和,即a2+3ab+2b2,因此有(a+2b)(a+b)=a2+3ab+2b2,故选:A.二.填空题(共6小题,满分18分)11.解:982﹣99×97=982﹣(98+1)(98﹣1)=982﹣(982﹣1)=982﹣982+1=1.故答案为:1.12.解:∵(a﹣b)2=13,ab=6,∴a2+b2=(a﹣b)2+2ab=13+12=25.故答案为:25.13.解:原式=(a﹣b)2+4c(a﹣b)+4c2=a2﹣2ab+b2+4ac﹣4bc+4c2.故答案为:a2﹣2ab+b2+4ac﹣4bc+4c2.14.解:(2b﹣3c+4)(3c﹣2b+4)﹣2(b﹣c)2,=[(2b﹣3c)+4][﹣(2b﹣3c)+4]﹣2(b﹣c)2,=16﹣(2b﹣3c)2﹣2(b﹣c)2,=16﹣4b2+12bc﹣9c2﹣2b2+4bc﹣2c2,=﹣6b2﹣11c2+16bc+16.15.解:原式=(1﹣)×××…×=×…×==.故答案为:.16.解:∵x﹣y=+1①,y﹣z=﹣1②,∴x﹣z=2③,则①2+②2+③2=(x﹣y)2+(y﹣z)2+(x﹣z)2=(+1)2+(﹣1)2+(2)2=14,即2(x2+y2+z2﹣xy﹣yz﹣yx)=14,∴x2+y2+z2﹣xy﹣yz﹣yx=7.故答案为:7.三.解答题(共6小题,满分52分)17.解:(a﹣b)2=a2﹣2ab+b2=a2+2ab+b2﹣4ab=(a+b)2﹣4ab.当(a+b)2=5,ab=﹣2时,(a﹣b)2=(a+b)2﹣4ab=5﹣4×(﹣2)=13.18.解:原式=x2+2xy+y2﹣2(2x2﹣xy﹣y2)=x2+2xy+y2﹣4x2+2xy+2y2=﹣3x2+4xy+3y2.19.解:(1)20212﹣2022×2020=20212﹣(2021﹣1)×(2021+1)=20212﹣(20212﹣1)=1;(2)112+13×66+392=112+13×2×3×11+392=112+2×11×39+392=(11+39)2=502=2500.(3)(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y)=9x2+9xy﹣2xy﹣2y2﹣(9x2﹣y2)=9x2+9xy﹣2xy﹣2y2﹣9x2+y2=7xy﹣y2.20.解:(1)∵=,∴===﹣4x•=32﹣4=5;(2)∵=,∴=+2=5+2=7,∵=,∴=﹣2=49﹣2=47.21.解:(1)图1中阴影部分的面积为边长为a,边长为b的面积差,即a2﹣b2,图2长方形的长为a+b,宽为a﹣b,因此面积为(a+b)(a﹣b),所以有a2﹣b2=(a+b)(a﹣b),故答案为:a2﹣b2=(a+b)(a﹣b);(2)①∵4a2﹣b2=24,∴(2a+b)(2a﹣b)=24,又∵2a+b=6,∴2a﹣b=24÷6=4,故答案为:4;②原式====.22.解:(1)∵图2面积可表示为(a+b)2或(a﹣b)2+4ab,∴可得(a+b)2=(a﹣b)2+4ab;(2)由(1)题结论(a+b)2=(a﹣b)2+4ab可得,(a﹣b)2=(a+b)2﹣4ab,∴a﹣b=±,∴当x+y=5,时,x﹣y=±====±4,(3)∵(a+b)2=a2+2ab+b2,∴ab=,∴当(2020﹣m)2+(m﹣2021)2=7时,(2020﹣m)(m﹣2021)====﹣3.。
人教版八年级上册14、2《乘法公式》同步练习带答案 基础巩固1 •下列添括号错误的是( )。
A.—x+5= —(x+5)C ・“2-3 = + (“2-3)2•下列各式,计算正•确的是( )A 。
(u —b)1 2 3=a 2—JrC. (a+h) — a 2^b 23•下列各式中,与(</-1) 2相等的是(2(宀一1Co a 2—2a — 14、下列等式能够成立的是().Ao (A —y) 2=x 2~xy+y 2Bo (x+3y)2=A 2+9rCo (x — - y )2=x 2—xy+ — y 2 2r 4'D.伽一9)(〃】+9)=〃】2—95o 应用乘•法公式计算:K 234 5?+2、469X0、765 5+0、765 52的值为 _____________ 。
6o 正方形的边长增大5 cm,而积增大75 cm —那么原正方形的边长为 _____________ ,面积为 _________ ・ 7o ( —a —b) (a~b) =一[() (a~b)^ =—[ ( )2 — ( )2]= __________ 、&计算:(1) (兀一3) X+9) (x+3): (2) (x+y —1) (x —y+1):9、(1)先化简,再求值:2 (3x+1)(1-3x) +(x~2) (2+x),其中 x=2、2⑵化简求值:(1一4$)(1+4巧+(1+4刃2,英中)=二、能力提升10•若工一)2=20,且 x+y=—5,贝'J x —y 的值是乂 )。
Ao 5 B.4C.-4 . D •以上都不对11。
等式(一“一b)( ) Ca 2+b 2) =a 4—b 4 中,括号内应填(Ao —a+b B.a~bC.—a — b .rD.d+b12o 若 a 2+2ab+b 2=(a-b)2+A 9 则 A 的值为( )。
Ao lab r Bo ~abCo 4ab Do ~4ab13。
2021——2022学年度人教版八年级数学上册 第十四章 整式的乘法与因式分解14.2 乘法公式 同步练习一、选择题1.下列计算正确的是( )A .(a +b )(a ﹣2b )=a 2﹣2b 2B .(a ﹣12)2=a 2﹣14C .﹣2a (3a ﹣1)=﹣6a 2+aD .(a ﹣2b )2=a 2﹣4ab +4b 22.多项式291x 加上一个单项式后﹐使它成为一个整式的完全平方,那么加上的单项式可以是( ) A .6x ± B .-1或4814x C .29x - D .6x ±或1-或29x -或4814x 3.若28x x k -+是完全平方式,则k 的值是( )A .4B .8C .16D .32 4.设, a b 是实数,定义一种新运算:()2*a b a b =-.下面有四个推断:①**a b b a =;①()222**a b a b =;①()()**a b a b -=-;①()**a b c a b a c +=+*. 其中所有正确推断的序号是( )A .①①①①B .①①①C .①①D .①①5.下列计算正确的是( )A .()222x y x y +=+B .()32626m m =C .()2224x x -=-D .()()2111x x x +-=-6.已知1x =,1y =,则代数式222x xy y ++的值为( ).A .20B .10C .D .7.若()()()248(21)2121211A =+++++,则A 的末位数字是( ) A .4 B .2 C .5 D .68.已知x +1,y ﹣1,则xy 的值为( )A .8B .48C .D .6 9.记A n =(1﹣212)(1﹣213)(1﹣214)…(1﹣21n ),其中正整数n ≥2,下列说法正确的是( ) A .A 5<A 6 B .A 52>A 4A 6C .对任意正整数n ,恒有A n <34D .存在正整数m ,使得当n >m 时,A n <10082015 10.如图:用四个全等的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用a ,b 分别表示矩形的长和宽(a b >),则下列关系中不正确的是( )A .12a b +=B .2a b -=C .35ab =D .2284a b += 二、填空题11,利用这个比例,我们规定一种“黄金算法”即:a ①b =a b ,比如1①2=×2x ①(4①8)=10,则x 的值为______.12.对于实数a ,b ,定义运算“*”:a *b =22,,a ab a b ab a a b⎧-≥⎨-<⎩,若x 1,x 2是一元二次方程x 2﹣5x +6=0的两个根,其中x 1>x 2,则x 1*x 2=____.13.已知2410x x -+=,则221x x +的值是___. 14.若8x y -=,10xy =,则22x y +=______________.15.希望小组的同学在求式子23411111 (22222)n a a a a a +++++的值(结果用n 和a 表示)时遇到了困难.经过合作探究他们想出了如图所示的图形来解释这个式子:设①ABC 的面积为a ,取BC 的中点,则有①ABD 的面积为12a ,再取AD 的中点E ,则有①ACE 的面积为212a ,再取CE 的中点F ,则有①DEF 的面积为312a ,......照此思路持续取下去.就可利用这个图形求得 23411111 (22222)n a a a a a +++++的值=___________.三、解答题16.计算(1)(2x )3(﹣5xy 2)(2)(﹣6a 2b )•(23b 2﹣13a ) (3)(3a +b )(a ﹣3b )(4)(3x +2y ﹣1)(3x ﹣2y +1)17.老师在数学课上提出这样一个问题:已知21(0)x x x +=-≠,求221x x +的值. 小明通过观察、分析、思考,形成了如下思路:先将等式两边都除以x ,得到1x x +的值,再利用完全平方公式求出221x x+. 参考小明的思路,解决下列问题:(1)已知210(0)x x x --=≠,求221x x +的值;(2)已知213(0)x x x +=≠18.一个正整数 A 若能写成A =m ²- n ²(m 、n 均为正整数,且m >n ),则称A 为“第一共同 体数”,m 、n 为A 的平方差分解数组.在A 的所有平方差分解数组中,若m - n 最大,则称m 、n 为A 的最佳平方差分解数组,此时 Q (A )= m ²+ n ².范例①:①13=7²﹣6²,①13为第一共同体数,7和6为13的平方差分解数组;范例①:32的平方差分解有两组,即 32=9²﹣7²,32=6²﹣2².① 6-2>9-7,①6和2为32的最佳平方差分解数组,Q (32)=6²+2²=40根据材料回答:(1)请模仿范例①写出两个10以内的“第一共同体数”,并写出它们的平方差分解数组;(2)判断 48 是否为第一共同体数?若不是,请说明理由,若是,请计算 Q (48)的值19.(1)对于算式()()()()()2481024212121212+1______++++=;不用计算器,你能计算出来吗?直接写出计算结果.(2)你计算结果的个位数字是________.(3)根据(1)推测()()()()()2420481111+1=_______m m m m m -+++.20.阅读下面的材料并解答后面的问题:在学了整式的乘法公式后,小明问:能求出243x x ++的最小值吗?如果能,其最小值是多少?小丽:能.求解过程如下:因为222434443(2)1x x x x x ++=++-+=+-,因为2(2)0x +≥,所以243x x ++的最小值是1-.问题:(1)小丽的求解过程正确吗?(2)你能否求出285x x -+的最小值?如果能,写出你的求解过程;(3)求265x x -+-的最大值.21.我们通常用作差法比较代数式大小.例如:已知M =2x +3,N =2x +1,比较M 和N 的大小.先求M ﹣N ,若M ﹣N >0,则M >N ;若M ﹣N <0,则M <N ;若M ﹣N =0,则M =N ,反之亦成立.本题中因为M ﹣N =2x +3﹣(2x +1)=2>0,所以M >N .(1)如图1是边长为a 的正方形,将正方形一边不变,另一边增加4,得到如图2所示的新长方形,此长方形的面积为S 1;将图1中正方形边长增加2得到如图3所示的新正方形,此正方形的面积为S 2用含a 的代数式表示S 1= ,S 2= (需要化简).然后请用作差法比较S 1与S 2大小;(2)已知A =2a 2﹣6a +1,B =a 2﹣4a ﹣1,请你用作差法比较A 与B 大小.(3)若M =(a ﹣4)2,N =16﹣(a ﹣6)2,且M =N ,求(a ﹣4)(a ﹣6)的值.22.观察:(1)如图1,已知正方形ABCD的边长为a,正方形FGCH的边长为b,长方形ABGE和长方形EFHD为阴影部分,则阴影部分的面积可表示为(写成平方差的形式);(2)将图1中的长方形ABGE和长方形EFHD剪下来,拼成如图2所示的长方形,则长方形AHDE的面积是(写成多项式相乘的形式);探究:(3)比较图1与图2的阴影部分的面积,可得等量关系;(4)若7x﹣y=5,y+7x=7,则49x2﹣y2=;应用:(5)利用公式计算:(1﹣13)(1+13)(1+213)(1+413)(1+813) (1)6413)+12813.23.(知识生成)通过不同的方法表示同一图形的面积,可以探求相应的等式,两个边长分别为a,b的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的梯形,请用两种方法计算梯形面积.(1)方法一可表示为;方法二可表示为;(2)根据方法一和方法二,你能得出a,b,c之间的数量关系是(等式的两边需写成最简形式);(3)由上可知,一直角三角形的两条直角边长为6和8,则其斜边长为.(知识迁移)通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是边长为a+b的正方体,被如图所示的分割线分成8块.(4)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为.(等号两边需化为最简形式)(5)已知2m﹣n=4,mn=2,利用上面的规律求8m3﹣n3的值.【参考答案】1.D 2.D 3.C 4.D 5.D 6.A 7.D 8.D 9.D 10.D11.12.3或2或313.1414.8415.12na a - 16.(1)4240-x y ;(2)23342ab a b -+;(3)22383a ab b --;(4)229441x y y -+-17.(1)221x x +=8+(2= 18.(1)7为第一共同体数,4和3为7的平方差分解数组,9为第一共同体数,5和4为9的平方差分解数组;(2)是,理由见解析,(48)50Q =19.(1)204821-;(2)5;(3)40961m -20.(1)正确;(2)能,最小值为-11,见解析;(3)4.21.(1)a 2+4a <a 2+4a +4;(2)A >B ;(3)622.(1)22a b -;(2)()()a b a b +-;(3)22()()a b a b a b -=+-;(4)35;(5)123.(1)12ab +12ab +12c 2;12(a +b )2;(2)c 2=a 2+b 2;(3)10;(4)(a +b )3=a 3+3a 2b +3ab 2+b 3;(5)8m 3﹣n 3的值为112.。
2022-2023学年人教版八年级数学上册《14.2乘法公式》同步题型分类练习题(附答案)一.完全平方公式1.下列运算正确的是()A.(a+4)2=a2+16B.a3•a4=a12C.(﹣a)4=﹣a4D.7x3﹣2x3=5x32.已知x2+4x+4=0,则x3的值等于()A.8B.2C.﹣3D.﹣83.已知M=(x+1)2+(2x+1)(2x﹣1),N=4x(x+1),当x=时,请比较M与N的大小.4.若a+2b=7,ab=6,则(a﹣2b)2的值是()A.3B.2C.1D.05.(2a+b)2=(2a﹣b)2+()A.4ab B.﹣4ab C.8ab D.﹣8ab6.若a+b=3,ab=2,则a2+b2的值是()A.2.5B.5C.10D.157.如果a﹣b=2,a﹣c=,那么a2+b2+c2﹣ab﹣ac﹣bc等于()A.B.C.D.不能确定8.已知a+=3,则a2+的值是.9.已知a+b=8,a2b2=4,则﹣ab=.10.若x2﹣4x﹣1=(x+a)2﹣b,则|a﹣b|=.11.若(a+b)2=9,(a﹣b)2=4,则a2+b2=.12.(1)若x+y=8,x2+y2=40,求xy的值;(2)请直接写出下列问题的答案:①若2a+b=5,ab=2,则2a﹣b=;②若(4﹣x)(5﹣x)=8,则(4﹣x)2+(5﹣x)2=.二.完全平方公式的几何背景13.如图,两个正方形的边长分别为a,b,如果a﹣b=2,ab=3,则图中阴影部分的面积是.14.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.(1)请根据拼图的原理,写出三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系;(2)根据(2)中等式,已知a+b=9,ab=8,求﹣b2+2ab﹣a2和b2﹣a2的值.三.完全平方式15.如果二次三项式x2﹣3x+a是一个完全平方式,那么常数a的值是.16.已知多项式x2+kx+1是一个关于x的完全平方式,则实数k=.四.平方差公式17.下列计算正确的是()A.6x5﹣2x2=4x3B.(﹣2x3)2=﹣4x6C.(﹣3x3)•(﹣x2)=3x5D.(x﹣2)(﹣x+2)=x2﹣418.已知a+b=2,a﹣b=1,则a2﹣b2=.19.已知a+b=10,a﹣b=8,则a2﹣b2=.20.计算:20202﹣2019×2021=.21.计算:(2+1)(22+1)(24+1)(28+1)=(结果可用幂的形式表示).22.怎样简便就怎样计算:(1)1232﹣124×122 (2)(2a+b)(4a2+b2)(2a﹣b)23.如果一个正方形的边长增加2cm,它的面积就增加24cm2,求原正方形的边长.五.平方差公式的几何背景24.实践与探索:如图1,边长为a的大正方形里有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).(1)上述操作能验证的等式是:(请选择正确的一个)A.a2﹣b2=(a+b)(a﹣b)B.a2﹣2ab+b2=(a﹣b)2C.a2+ab=a(a+b)(2)请应用这个等式完成下列各题:①已知4a2﹣b2=24,2a+b=6,则2a﹣b=.②计算:9(10+1)(102+1)(104+1)(108+1)(1016+1).25.如图,将4个长、宽分别为a,b的长方形摆成一个大正方形(不重叠),利用面积的不同表示方法写出一个代数恒等式是()A.(a+b)(a﹣b)=a2﹣b2B.(a+b)2﹣(a﹣b)2=4abC.(a+b)2=a2+2ab+b2D.(a﹣b)2=a2﹣2ab+b2参考答案一.完全平方公式1.解:A、原式=a2+8a+16,故A符合题意.B、原式=a7,故B不符合题意.C、原式=a4,故C不符合题意.D、原式=5x3,故D符合题意.故选:D.2.解:∵x2+2x+4=0,∴(x+2)2=0,解得:x=﹣2,∴x3=(﹣2)3=﹣8.故选:D.3.解:∵M=(x+1)2+(2x+1)(2x﹣1),N=4x(x+1),∴M﹣N=(x+1)2+(2x+1)(2x﹣1)﹣4x(x+1)=x2+2x+1+4x2﹣1﹣4x2﹣4x=x2﹣2x,∵x=,∴x2﹣2x=2﹣2<0,∴M﹣N<0,∴M<N.4.解:(a﹣2b)2=a2+4b2﹣4ab=a2+4b2+4ab﹣8ab=(a+2b)2﹣8ab,∵a+2b=7,ab=6,∴原式=72﹣8×6=49﹣48=1.故选:C.5.解:∵(2a+b)2=4a2+b2+4ab,(2a﹣b)2=4a2+b2﹣4ab,∴(2a+b)2﹣(2a﹣b)2=8ab.∴(2a+b)2=(2a﹣b)2+8ab.故选:C.6.若a+b=3,ab=2,则a2+b2的值是()A.2.5B.5C.10D.15解:a2+b2=(a+b)2﹣2ab=32﹣2×2=5.故选:B.7.如果a﹣b=2,a﹣c=,那么a2+b2+c2﹣ab﹣ac﹣bc等于()A.B.C.D.不能确定解:a2+b2+c2﹣ab﹣ac﹣bc,=×(2a2+2b2+2c2﹣2ab﹣2ac﹣2bc),=×[(a2+b2﹣2ab)+(a2+c2﹣2ac)+(b2+c2﹣2bc)],=×[(a﹣b)2+(a﹣c)2+(b﹣c)2],∵a﹣b=2,a﹣c=,∴b﹣c=﹣,∴原式=×(4++)=.故选:A.8.已知a+=3,则a2+的值是7.解:∵a+=3,∴a2+2+=9,∴a2+=9﹣2=7.故答案为:7.9.已知a+b=8,a2b2=4,则﹣ab=28或36.解:﹣ab=﹣ab=﹣ab﹣ab=﹣2ab∵a2b2=4,∴ab=±2,①当a+b=8,ab=2时,﹣ab=﹣2ab=﹣2×2=28,②当a+b=8,ab=﹣2时,﹣ab=﹣2ab=﹣2×(﹣2)=36,故答案为28或36.10.解:∵(x+a)2﹣b=x2+2ax+a2﹣b,∴2a=﹣4,a2﹣b=﹣1,解得a=﹣2,b=5,∴|a﹣b|=|﹣2﹣5|=7.故本题的答案是7.11.解:由完全平方公式(a+b)2=a2+2ab+b2和(a﹣b)2=a2﹣2ab+b2,可得,∵(a+b)2=9,(a﹣b)2=4,∴==6.5.故答案为:6.5.12.解:(1)∵(x+y)2=x2+2xy+y2,∴82=40+2xy,∴xy=12.(2)①∵(2a﹣b)2=(2a+b)2﹣8ab,∴2a﹣b==±3;②(4﹣x)2+(5﹣x)2=[(4﹣x)﹣(5﹣x)]2+2(4﹣x)(5﹣x)=1+2×8=17.二.完全平方公式的几何背景13.解:S阴影=S△BCD﹣S△BEF﹣S正方形CGEF=====;∵a﹣b=2,ab=3,∴(a+b)2=(a﹣b)2+4ab(a+b)2=4+12,(a+b)2=16,∴a+b=±4,∵a,b都是边长,∴a+b=4.∴S阴影=;=﹣=.故答案为:.14.解:(1)大正方形的边长为m+n,因此面积为(m+n)2,阴影小正方形的边长为m﹣n,因此面积为(m﹣n)2,而每个长方形的面积为mn,由S大正方形=S小正方形+4S长方形可得,(m+n)2=(m﹣n)2+4mn,故答案为:(m+n)2=(m﹣n)2+4mn;(2)由(1)得,(a+b)2=(a﹣b)2+4ab,即81=(a﹣b)2+32,∴a﹣b=±7.∴﹣b2+2ab﹣a2=﹣(b2﹣2ab+a2)=﹣(a﹣b)2=﹣49,∴b2﹣a2=(a+b)(b﹣a)=9×(±7)=±63.三.完全平方式15.解:∵(x﹣)2=x2﹣3x+,∴a=,故答案为:.16.解:∵多项式x2+kx+1是一个关于x的完全平方式,∴x2+kx+1=(x±1)2=x2±2x+1,∴k=±2,故答案为:±2.四.平方差公式17.解:A、6x5与﹣2x2不是同类项,故不能合并,故A不符合题意.B、原式=4x6,故B不符合题意.C、原式=3x5,故C符合题意.D、原式=﹣(x﹣2)2=﹣x2+4x﹣4,故D不符合题意.故选:C.18.解:因为a+b=2,a﹣b=1,则a2﹣b2=(a+b)(a﹣b)=2×1=2.故答案为:2.19.已知a+b=10,a﹣b=8,则a2﹣b2=80.解:∵(a+b)(a﹣b)=a2﹣b2,∴a2﹣b2=10×8=80,故答案为:8020.计算:20202﹣2019×2021=1.解:20202﹣2019×2021=20202﹣(2020﹣1)×(2020+1)=20202﹣20202+12=1 故答案为:1.21.计算:(2+1)(22+1)(24+1)(28+1)=216﹣1(结果可用幂的形式表示).解:(2+1)(22+1)(24+1)(28+1),=(2﹣1)(2+1)(22+1)(24+1)(28+1),=(22﹣1)(22+1)(24+1)(28+1),=(24﹣1)(24+1)(28+1),=(28﹣1)(28+1),=216﹣1.22.怎样简便就怎样计算:(1)1232﹣124×122(2)(2a+b)(4a2+b2)(2a﹣b)解:(1)1232﹣124×122=1232﹣(123+1)(123﹣1)=1232﹣(1232﹣1)=1232﹣1232+1=1;(2)(2a+b)(4a2+b2)(2a﹣b)=(2a+b)(2a﹣b)(4a2+b2)=(4a2﹣b2)(4a2+b2)=(4a2)2﹣(b2)2=16a4﹣b4.23.如果一个正方形的边长增加2cm,它的面积就增加24cm2,求原正方形的边长.解:设原正方形的边长为xcm,(x+2)2﹣x2=24,解得:x=5.答:原正方形的边长为5cm.五.平方差公式的几何背景24.解:(1)图1中阴影部分面积可以表示为a2﹣b2或(a+b)(a﹣b),故选:A;(2)①由(1)题结果可得,(2a+b)(2a﹣b)=4a2﹣b2,∴2a﹣b=(4a2﹣b2)÷(2a+b)=24÷6=4,故答案为:4,②∵9(10+1)(102+1)(104+1)(108+1)(1016+1)=(10﹣1)(10+1)(102+1)(104+1)(108+1)(1016+1),∴由(1)题结果可得,原式=(102﹣1)(102+1)(104+1)(108+1)(1016+1)=(104﹣1)(104+1)(108+1)(1016+1)……=1032﹣1.25.解:总体大正方形的边长为a+b,因此面积为(a+b)2,中间小正方形的边长为a﹣b,因此面积为(a﹣b)2,4个长方形的面积为4ab,根据各个部分面积之间的关系可得,(a+b)2﹣(a﹣b)2=4ab,故选:B.。