高一数学下册练习七试题

高一下学期期末考试数学试题07（含答案)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.满分150分,考试时间120分钟.第I 卷 （选择题 共60分）一、选择题:本大题共12小题，每题5分，共60分。

每小题给出的四个选项中，只有一项符合题目要求。

1、已知集合{}2,0,2A =-,{}2=20B x x x --=，则A B=（ ）2、不等式22x x ≥的解集是（ ）A ．{}2x x ≥ {}.2B x x ≤ {}.02C x x≤≤ {}.02D x x x ≤≥或 3、经过两直线1:2320l x y -+=与2:3420l x y --=的交点，且平行于直线4270x y -+=的直线方程是（ ）A ．290x y -+=B ．4290x y -+=C ．2180x y --=D ．2180x y ++= 4、已知a b >，则下列不等式一定成立的是（ ）A. 11a b< B.1122ab⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭C. ln ln a b >D. 33a b > 5、已知向量(1)(1)n n ==-，，，a b ，若2-a b 与b 垂直，则=a ( ) A ．2BC ．1D ．46、在△ABC 中，角A ，B ，C 所对的边分别为,,a b c ,若2cos a b C =，则这个三角形一定是（ ） A ．等边三角形 B ．直角三角形 C ．等腰三角形 D ．等腰直角三角形7、过点(2,2)P 的直线与圆22(1)5x y -+=相切，且与直线10ax y -+=垂直，则a =( ) A ．12-B ．1C ．2 D.128、设0.13592,ln,log 210a b c ===，则,,a b c 的大小关系是（ ） A. a b c >> B. a c b >> C. b a c >> D.b c a >>9、已知D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则（ ） A ．0BD BE FC --= B ．0BD CF DF -+= C．0AD CE CF +-=D ．0AD BE CF ++=10、已知0ω>，2π<ϕ，函数()sin()f x x =+ωϕ的部()sin g x x =ω的图象，只分图象如图所示．为了得到函数要将()f x 的图象（ ）A.∅B. {}2C. {}0D. {}2-A ．向右平移4π个单位长度 B ．向右平移8π个单位长度 C ．向左平移4π个单位长度 D ．向左平移8π个单位长度11、在三棱柱111ABC A B C -中，已知1AA ABC ⊥平面,12,2AA BC BAC π==∠=，此三棱柱各个顶点都在一个球面上，则球的体积为（ ）A ．323π B ．16π C ．253π D ．312π12、[]x 表示不超过x 的最大整数，例如[][]2.92, 4.15=-=-，已知[]()f x x x =-，()x R ∈，4()log (1)g x x =-，则函数()()()h x f x g x =-的零点个数为（ ）A ．4B ．3C ．2D ．1第II 卷 （非选择题 共90分）二、填空题：本大题共4小题，每题5分，共20分。

卜人入州八九几市潮王学校赣榆区二零二零—二零二壹高一数学下学期期末复习综合训练7一、填空题：本大题一一共14小题，每一小题5分，一共计70分．1．tan300°=2．角的终边经过点P (2，－1)，那么sin 的值是▲．3.圆x 2+y 2﹣x+2y=0的圆心坐标为．4．扇形的半径为3cm ，圆心角为2弧度，那么扇形的面积为▲cm 2． 5．以下图是一个算法流程图，那么输出的a 的值________.〔第5题〕〔第6题〕6．如图算法的伪代码，输出的结果是________f (x )＝cos(x －)，x [0，]的值域是▲． y ＝sin2x的图象向右平移个单位长度，所得图象的函数解析式是▲． 9.点)3,1(A 在圆4:22=+y x C 上，那么过点A 的圆C 的切线方程为▲．10．如图，在矩形ABCD 中，AB ＝3，AD ＝2， 且＝，＝，那么·＝▲． 11.函数y =的值域是 ．12．在△ABC 中，(＋)·＝||2，那么△ABC 的形状一定是________三角形.ABCD 的边长为2，120BAD ∠=，点,E F 分别在边,BC DC 上，BE BC λ=，DF DC μ=.假设1AE AF ⋅=，23CE CF ⋅=-，那么λμ+=________. 14．实数a b c 、、满足222a b c +=，0c ≠，那么2b a c-的取值范围为． A B CD EF 〔第10题〕 S ←0For I From1To10S ←S ＋I EndForPrint S二、解答题：本大题一一共6小题，一共计90分．解答时应写出文字说明、证明过程或者演算步骤．15.△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .向量m ＝(a ，b )与n ＝(cos A ，sin B )平行.(1)求A ；(2)假设a ＝，b ＝2，求△ABC 的面积.16．设函数)sin()(ϕω+=x A x f 〔A ，ω，ϕ为常数，且A ＞0，ω＞0，0＜ϕ＜π〕的局部图象如以下图．〔1〕求A ，ω，ϕ的值；〔2〕当x ∈[0，]时，求)(x f 的取值范围．17．如图，在四边形ABCD 中，△ABC 是边长为6的正三角形，设〔x ，y ∈R 〕．BC y BA x BD +=〔1〕假设x=y=1，求|BD |；〔2〕假设BC BD ⋅=36，BA BD ⋅=54，求x ，y ．18.向量m ＝，n ＝.(1)假设n m ⋅＝1，求cos 的值；(2)记f (x )＝n m ⋅，在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且满足(2a －c )cos B ＝b cos C ，求函数f (A )的取值范围.19．如以下图，∠PAQ 是村里一个小湖的一角，其中∠PAQ=60°．为了给村民营造丰富的休闲环境，村委会决定在直线湖岸AP 与AQ 上分别建观光长廊AB 与AC ，其中AB 是宽长廊，造价是800元/米；AC 是窄长廊，造价是400元/米；两段长廊的总造价预算为12万元〔恰好都用完〕；同时，在线段BC 上靠近点B 的三等分点D 处建一个表演舞台，并建水上通道AD〔表演舞台的大小忽略不计〕，水上通道的造价是600元/米．〔1〕假设规划宽长廊AB与窄长廊AC的长度相等，那么水上通道AD的总造价需多少万元？〔2〕如何设计才能使得水上通道AD的总造价最低？最低总造价是多少万元？20．O为坐标原点，设动点M〔2，t〕〔t＞0〕．〔1〕假设过点P〔0，4〕的直线l与圆C：x2+y2﹣8x=0相切，求直线l的方程；〔2〕求以OM为直径且被直线3x﹣4y﹣5=0截得的弦长为2的圆的方程；〔3〕设A〔1，0〕，过点A作OM的垂线与以OM为直径的圆交于点N，求证：线段ON的长为定值，并求出这个定值．。

练习题(七)班级 姓名 考号 考场号密封线内不得答题一、选择题（每小题3分，共36分）1、在等差数列8、5、2… 中20a 为A. 65B. －52C. －49D. －20 2、公差不为0的等差数列{}n a 中，236,,a a a 成等比数列，则公比q 为 A. 1 B. 2 C. 3 D. 43、在等比数列{}n a 中，7114146,5a a a a =+=，则2010aa =A.23 B. 32 C. 2332或 D. 233－或－24、设x y ≠,以下的数12,,,x a a y 和123,,,,x b b b y 分别是不同的等差数列,那么2132a ab b --的值为A. 23B. 1C. 34D. 435、在等差数列{}n a 中，10120,S =那么110a a +的值为A. 12B. 24C. 36D. 486、等差数列{}n a 的前n 项和22n S n n =+，那么它的通项公式为A.21n a n =-B. 21n a n =+C. 41n a n =+D. 41n a n =- 7、已知{}n a 是等比数列，31,2a q ==，则5a =A. 2B. 4C. 12D. －48、已知等差数列{}n a 中，1626log 2,log 3a a ==，则3a = A. 0 B. 69log 2C. 1D. 4 9、在等比数列{}n a 中，35a a 和是二次方程250x kx ++=的两根，则246a a a 的值为A. ±B.-10、首项为125，第10项为开始比1大的项，此数列的公差的取值范围是A. 875d >B. 325d <C. 382525d <<D. 837525d <≤ 11、设{}n a 是正数组成的等比数列，且公比1q ≠，则1845a a a a ++与的大小关系是 A. 1845a a a a +>+ B. 1845a a a a +<+ C. 1845a a a a +=+ D. 与公比的值有关 12、已知,,a b a b +成等差数列，,,a b ab 成等比数列，0log ()1m ab <<，则m 的取值范围是 A. 8m > B. 1m > C. 18m << D. 018m m <<>或二、填空题（每小题3分，共12分） 13、在数列1,1,2,3,5,8,13,,34,55,x 中，x 的值为_____________14、已知等差数列的前n 项和223n S n n c =++，则c ＝_____________15、在等比数列{}n a 中，若2348,60,_________n n n S S S === 16、在等比数列{}n a 中，若510152,10,__________a a a ===则三、解答题（共6小题，共52分）17、（6分）已知数列{}n a 是等差数列,221n n n b a a +=-,求证: {}n b 也是等差数列18、（8分）在等比数列{}n a 中，52a =，求： （1）19283746a a a a a a a a +++的值 （2）1239a a a a 的值19、（8分）已知数列{}n a 前n 项和为n S ，且*lg(1)()n S n n N +=∈，证明：数列{}n a 是等比数列20、10分）求和11111111(1)(1)(1)224242n n S -=+++++++++++21、（10分）设集合{|2,},{|3,}A x x n n Z B x x k k Z ==∈==∈集合，集合{|||60,[0,)}C x x x =≤∈+∞，求：A B C 的元素和是多少？22、、（10分）数列{}n a 的前n 项和为11,1,21,(1)n n n S a a S n +==+≥。

高一（下）数学练习七——诱导公式、两角和与差的余弦、正弦 一．填空题：1．已知)6cos(ϑπ+＝33，则)65cos(ϑπ-＝ ． 2．已知βsin ＝31，)sin(βα+＝1，则)2sin(βα+＝ ． 3．设)(n f ＝)4sin(απ+n ，则)4()(+⋅n f n f ＋)6()2(+⋅+n f n f ＝ ． 4．已知)(x f ＝x ＋2ax ＋x b cos ，且)12(πf ＝4π，则)12(π-f ＝ ． 5．已知αsin ＋αcos ＝51，α是第二象限角，则αtan ＝ ． 6．若实数x 满足x 2log ＋ϑcos ＝2，则|x －8|＋|x －2|＝ ．7．若αtan ＋αcot ＝－2，则αsin ＋αcos ＝ ．8．已知αtan ＝3，则αααα22cos sin cos sin 21-+＝ ． 9．化简：ααααsin tan tan sin -－ααcos sin 1+＝ ． 10．已知ααcos sin ⋅＝81，且4π＜α＜2π，则αcos －αsin ＝ ． 11．已知α、β均为锐角，αtan ＝43，βcos ＝21，则)cos(βα+＝ ． 12．已知锐角α、β满足αcos ＝53，)cos(βα+＝－135，则βcos ＝ ． 二．选择题：13．)(sin 2απ+－)cos()cos(ααπ-+＋1的值是（ ）（A ）1； （B ）2α2sin ； （C ）0； （D ）2．14．若2πk －4π≤α≤2πk ＋4π(k ∈Z )，化简ααcos sin 21-＋ααcos sin 21+，所得结果是（ ） （A ）2αsin ； （B ）－2αsin ； （C ）2αcos ； （D ）－2αcos ． 15．若αsin 、αcos 是方程32x ＋6mx ＋2m ＋1＝0的两根，则实数m 的值为（ ）（A ）－21； （B ）65； （C ）－21或65； （D ）21． 16．若x x 3cos 2cos ＝x x 3sin 2sin ，则x 的一个值是（ ） （A ）36 ； （B ）45 ； （C ）18 ； （D ）30．三．解答题：17．已知)3sin(απ-＝)2sin(2βπ+，)cos(3α-＝－)cos(2βπ+，且0＜α＜π，0＜β＜π，求αsin 、βsin ．解：18．化简：（1）613cos 3422πm ＋36tan 22πn －417cos 222πn －3sin 3122πm ； （2） 810sin 2a ＋ 765tan 2b ＋ 1125cot )(22b a -－2 720cos ab ．解：19．已知0＜β＜4π，4π＜α＜43π，且)4cos(απ-＝53，)43sin(βπ+＝135，求)sin (βα+的值．解：20．如果方程2x －4ϑ2cos x ＋2＝0的一个根和22x ＋4ϑ2sin x －1＝0的一个根互为倒数，求ϑ(0＜ϑ＜π)．解：高一数学练习七——诱导公式、两角和与差的余弦、正弦一．填空题： 1．已知)6cos(ϑπ+＝33，则)65cos(ϑπ-＝ －33 ． 2．已知βsin ＝31，)sin(βα+＝1，则)2sin(βα+＝ 31 ． 3．设)(n f ＝)4sin(απ+n ，则)4()(+⋅n f n f ＋)6()2(+⋅+n f n f ＝ －1 ． 4．已知)(x f ＝x ＋2ax ＋x b cos ，且)12(πf ＝4π，则)12(π-f ＝ 12π ． 5．已知αsin ＋αcos ＝51，α是第二象限角，则αtan ＝ －34 ． 6．若实数x 满足x 2log ＋ϑcos ＝2，则|x －8|＋|x －2|＝ 6 ．7．若αtan ＋αcot ＝－2，则αsin ＋αcos ＝ 0 ．8．已知αtan ＝3，则αααα22cos sin cos sin 21-+＝ 2 ． 9．化简：ααααsin tan tan sin -－ααcos sin 1+＝ 0 ． 10．已知ααcos sin ⋅＝81，且4π＜α＜2π，则αcos －αsin ＝ －23 ． 11．已知α、β均为锐角，αtan ＝43，βcos ＝21，则)cos(βα+＝ －1411 ． 12．已知锐角α、β满足αcos ＝53，)cos(βα+＝－135，则βcos ＝ 6533 ． 二．选择题：13．)(sin 2απ+－)cos()cos(ααπ-+＋1的值是（ D ）（A ）1； （B ）2α2sin ； （C ）0； （D ）2．14．若2πk －4π≤α≤2πk ＋4π(k ∈Z )，化简ααcos sin 21-＋ααcos sin 21+，所得结果是（ C ）（A ）2αsin ； （B ）－2αsin ； （C ）2αcos ； （D ）－2αcos ．15．若αs in 、αcos 是方程32x ＋6mx ＋2m ＋1＝0的两根，则实数m 的值为（ A ）（A ）－21； （B ）65； （C ）－21或65； （D ）21． 16．若x x 3cos 2cos ＝x x 3sin 2sin ，则x 的一个值是（ C ） （A ）36 ； （B ）45 ； （C ）18 ； （D ）30 ．三．解答题：17．已知)3sin(απ-＝)2sin(2βπ+，)cos(3α-＝－)cos(2βπ+，且0＜α＜π，0＜β＜π，求αsin 、βsin ．解：αsin ＝22，βsin ＝21．18．化简：（1）613cos 3422πm ＋36tan 22πn －417cos 222πn －3sin 3122πm ； （2） 810sin 2a ＋ 765tan 2b ＋ 1125cot )(22b a -－2 720cos ab ．解：（1）原式＝243m ； （2）原式＝22a －2ab ．19．已知0＜β＜4π，4π＜α＜43π，且)4cos(απ-＝53，)43sin(βπ+＝135，求)sin (βα+的值．解：∵－2π＜4π－α＜0，∴)4sin(απ-＝－54； ∵43π＜43π＋β＜π，∴)43cos(βπ+＝－1312． ∵)43(βπ+－)4(απ-＝α＋β＋2π， ∴)sin(βα+＝－)2cos(βαπ++＝－)]4()43cos[(απβπ--+＝6556．20．如果方程2x －4ϑ2cos x ＋2＝0的一个根和22x ＋4ϑ2sin x －1＝0的一个根互为倒数，求ϑ(0＜ϑ＜π)．解：设2x －4ϑ2cos x ＋2＝0的一个根为a ，则2a －4ϑ2cos a ＋2＝0 ① 221a＋4a ϑ2sin －1＝0，得：2a －4ϑ2sin a －2＝0 ② 两式相加得：a ＝2)2cos 2(sin ϑϑ+，代入得：ϑ2tan 2＝31， ϑ2tan ＝33，∴ϑ＝12π，125π，127π，1211π．。

2021年高一下学期数学期末复习综合练习（七）1. 已知，是非零向量，且，的夹角为，若向量，则 ▲2．已知函数，若，且在区间内有最大值，无最小值，则 ▲ ．3. 连续两次掷一颗质地均匀的骰子（一种各面上分别标有1，2，3，4，5，6个点的正方体玩具），记出现向上的点数分别为，设向量，，则与的夹角为锐角的概率是 ▲4. 已知函数，将的图象上各点的横坐标伸长为原来的倍，纵坐标不变，再将所得图象向右平移个单位，得到函数的图象，则函数的解析式为_____________________.5. 设为不重合的两条直线，为不重合的两个平面，给出下列命题：（1）若∥且∥，则∥；（2）若且，则∥；（3）若，则一定存在平面，使得；（4）若，则一定存在直线，使得.上面命题中，所有真命题．．．的序号是 ．6. 已知α、β为锐角，且tan α＝12，cos β＝31010，则sin(α＋β)＝________.7. 若函数y=cosx (不为0)在(0,)上是单调函数，则实数的取值范围是____________.8.已知扇形的圆心角为（定值），半径为（定值），分别按图一、二作扇形的内接矩形，若按图一作出的矩形面积的最大值为，则按图二作出的矩形面积的最大值为 .９．已知点P 在直线0），且y 0>x 0+2，则的取值范围为10. 在△ABC 中，，D 是BC 边上任意一点（D 与B 、C 不重合），且，则等于 ▲ ．11.与直线相切，且与圆相内切的半径最小的圆的方程是 ▲ .12.已知是边长为4的正三角形，D 、P 是内部两点，且满足，则的面积为13.如果圆上总存在两个点到原点的距离为1，则实数的取值范围是 ．14.平面直角坐标系中，已知点A （１，－２），B （４，０），Ｐ（ａ，１），Ｎ（ａ＋１，１），当四边形PABN 的周长最小时，过三点A 、P 、N 的圆的圆心坐标是715.（本题14分）已知为坐标原点，2(2sin ,1),(1,cos 1)OA x OB x x ==-+，.（Ⅰ）求的单调递增区间；（Ⅱ）若的定义域为，值域为，求的值.图一 第8题图图二16.设向量(4cos ,sin ),(sin ,4cos ),(cos ,4sin )ααββββ===-a b c（1）若与垂直，求的值；（2）求的最大值;（3）若∥，求的值。

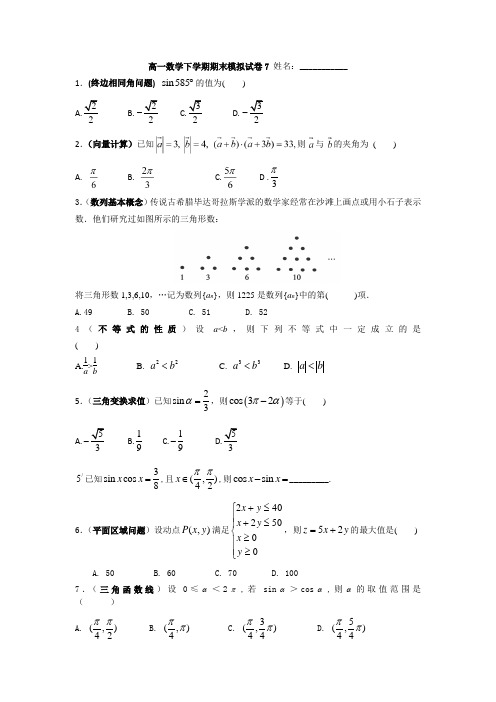
高一数学下学期期末模拟试卷7 姓名：___________1．(终边相同角问题) 的值为( )B.D.2．（向量计算）已知则与的夹角为 ()A.B.C.D .3π3．（数列基本概念）传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数．他们研究过如图所示的三角形数：将三角形数1,3,6,10，…记为数列{a n }，则1225是数列{a n }中的第( )项． A.49 B. 50 C. 51 D. 52 4（不等式的性质）设a <b ，则下列不等式中一定成立的是( )A.1a >1bB. 22a b <C. 33a b < D. a b < 5．（三角变换求值）已知2sin 3α=，则()cos 32πα-等于( ) A.3-B.19C.19-D.3/5已知3sin cos 8x x =,且(,)42x ππ∈,则cos sin x x -=_________.6．（平面区域问题）设动点),(y x P 满足⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00502402y x y x y x ，则y x z 25+=的最大值是( )A. 50B. 60C. 70D. 1007．（三角函数线）设0≤α＜2π,若sin α＞cos α,则α的取值范围是（ ） A. (,)42ππ B. (,)4ππ C. 3(,)44ππ D. 5(,)44ππ sin 585︒8.等差数列基本计算）已知{}n a 是公差为2的等差数列，且317111a a a +++是与的等比中项, 则数列{}n a 的通项公式；（ ）A. 21n -B. 21n +C. 2nD. 32n + 9．（向量坐标形式计算）设,,x y ∈R 向量(,1),(1,),(a x b y c a c bc ab===-⊥+且则（ ）A B C ．D ．1010．（图象变换）把函数=()y sin x x R ∈的图象上所有的点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变)，得到的图象所表示的函数是( ) A 、=(2-),R 3y sin x x π∈ B 、=(+),R 26x y sin x π∈ C 、=(2+),R 3y sin x x π∈ D 、 2=(2+),R 3y sin x x π∈ 11．（三角函数图象）函数)2||,0,0)(sin()(πϕωϕω<>>+=A x A x f 的部分图象如图所示.( )A. ()sin(2)12f x x π=+B. ()sin()6f x x π=+C. ()sin(2)3f x x π=+D. ()sin(2)6f x x π=+12(解三角形与三角变换）在∆ABC 中,A,B,C 为内角,且sin cos sin cos A A B B =,则∆ABC 是 ( ) A.等腰三角形 B.直角三角形C.等腰直角三角形D.等腰或直角三角形二,填空题(每题3分,共18分) 13．(已知三角函数值求角) 边长为的三角形的最大角与最小角的和是________14．(利用基本不等式求最值)求已知xy y x R y x ，则，且14,=+∈+的最大值为 15．(向量计算) 若向量a ，b 满足|a |=1，|b |=2且a 与b 的夹角为3π,则|a +b |=______ 16．(三角函数性质) 关于函数()x x x f 2cos 2sin -=有下列命题： ①函数()x f y =的周期为π；②直线4π=x 是()x f y =的一条对称轴； ③点⎪⎭⎫⎝⎛0,8π是()x f y =的图象的一个对称中心； ④将()x f y =的图象向左平移4π个单位，可得到x y 2sin 2=的图象.其中真命题的序号是______.（把你认为真命题的序号都写上） 17 (等差数列前n 项和问题) 在等差数列中，912162a a =+，则数列的前11项和S 11等于_______18(解三角形与三角变换) 在△ABC 中，角A ，B ，C 的对边为a ，b ，c ，若45a ==︒，则角A= 。

高一数学下(7)三角恒等变换单元测试10=（ ）A ．1B ．2CD 2．函数))(6cos()3sin(2R x x x y ∈+--=ππ的最小值等于（ ）A ．3-B ．2-C ．1-D ．3．函数2sin cos y x x x =的图象的一个对称中心是（ ）A .2(,3π B .5(,6πC .2(3π- D .(,3π4．△ABC 中，090C ∠=，则函数2sin 2sin y A B =+的值的情况（ ）A ．有最大值，无最小值B ．无最大值，有最小值C ．有最大值且有最小值D ．无最大值且无最小值5．0000(1tan 21)(1tan 22)(1tan 23)(1tan 24)++++ 的值是( )A . 16B . 8C . 4D . 26．当04x π<<时,函数22cos ()cos sin sin xf x x x x=-的最小值是（ ）A ．4B ．12 C ．2 D ．147．设212tan13cos66,,221tan 13a b c =-==+则有（ ） A.a b c >> B.a b c << C.a c b << D.b c a <<9．函数221tan 21tan 2xy x-=+的最小正周期是( ) A ．4π B ．2πC ．πD ．2π 9．已知3sin(),45x π-=则sin 2x 的值为（ ） A.1925 B.1625 C.1425 D.72510．若(0,)απ∈，且1cos sin 3αα+=-，则cos 2α=( )A ．917 B ． C ． D ．31711．已知在ABC ∆中，3sin 4cos 6,4sin 3cos 1,A B B A +=+=则角C 的大小为 ．12．计算：oo o oo o 80cos 15cos 25sin 10sin 15sin 65sin －＋的值为_______．13．函数22sincos()336x x y π=++的图象中相邻两对称轴的距离是 ． 14．函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于 ． 15．已知)sin()(ϕω+=x A x f 在同一个周期内，当3π=x 时，)(x f 取得最大值为2，当0=x 时，)(x f 取得最小值为2-，则函数)(x f 的一个表达式为______________16.求值：（1）000078sin 66sin 42sin 6sin ；（2）00020250cos 20sin 50cos 20sin ++。

卜人入州八九几市潮王学校塘栖二零二零—二零二壹高一数学下学期期末复习试题七一、选择题〔每一小题3分，一共30分〕 1、以下说法正确的选项是〔〕 A.*0N ∈ B.Q ∈2 C.Φ∈0 D.Z ∈-22、设全集U 是实数集R ，},112|{},4|{2≥-=>=x x N x x M 那么图中阴影局部所表示的集合是〔〕A ．}12|{<≤-x xB ．}22|{≤≤-x xC ．}21|{≤<x x D ．}2|{<x x3、以下函数中，值域是），（∞+0的是()4、函数x x x f cos sin )(+=的最小正周期是〔〕A ．π2B ．πC ．2πD ．4π5、点从()0,1出发，沿单位圆逆时针方向运动34π弧长到达Q 点，那么Q 点的坐标为〔〕A ．⎪⎪⎭⎫ ⎝⎛-23,21B ．⎪⎪⎭⎫ ⎝⎛--21,23C ．⎪⎪⎭⎫ ⎝⎛--23,21D ．⎪⎪⎭⎫⎝⎛-21,23 6、设ααα2sin )cos (sin =+f ，那么)51(f 的值是〔〕A ．2425-B ．1225-C ．2425D ．12257、,10ln ,lg ==b e a 那么〔〕A 、1>>b aB 、1>>a bC 、a b >>1D 、b a >>1 8、函数)(x f =)sin(ϕω+x ∈x (R ))20(πϕω<>,的局部图像如下列图，假设)3,6(,21ππ-∈x x ，且)()(21x f x f =，那么=+)(21x x f ()A ．21B ．22C ．23D ．19、ABC ∆的外接圆半径和ABC ∆的面积都等于1，那么C B A sin sin sin ⋅⋅=〔〕xyO6π-3π1〔第8题〕A ．14B ．12C.23C.4310、)3,0(),0,3(B A ，O 为坐标原点，点C 在第一象限内，且︒=∠60AOC ，设)(R OB OA OC ∈+=λλ，那么λ等于〔〕A.33B.3C.31D.3 二、填空题〔每一小题4分，一共6小题〕11、化简=⋅÷⋅-⋅⋅)21()2(656131212132b a b a b a 12、求出⎪⎩⎪⎨⎧≥++≤-≥+-010201y x x y x 所在的区域的面积ABC ∆中，角,,A B C 所对的边分别是,,a b c ，假设222b c a bc +=-，4AC AB ⋅=-且，那么ABC ∆的面积等于___．14、等比数列{}n a 的前项和为n S ，假设4562S S S =+，那么数列{}n a 的公比的值是。

心尺引州丑巴孔市中潭学校高一数学期末总复习“重温经典〞系列7一、填空题1．求值： 15sin 285sin 15cos 75cos -= ． 2. 5ππsin cos 88⋅= ．3. 在ABC ∆中，tantan tan A B A B +=C = ． 4. 假设()π1sin 63α+=，()ππ2α∈，，那么()πcos 12α-= ．5. ABC ∆的三个内角为A B C 、、，那么cos 2cos 2B CA ++的最大值为 ．6. cos α=，3ππ,2α⎛⎫∈ ⎪⎝⎭，且()tan 3αβ-=，那么tan β= ． 7．1cos 7α=，13cos()14αβ-=，且02πβα<<<，那么β= . 8. sin 3sin()6παα=+，那么tan()12πα+= ． 9．πππ,,,0222αβ⎛⎫⎛⎫∈-∈- ⎪ ⎪⎝⎭⎝⎭，且()()1tan 1tan 2αβ--=，那么αβ+= ． 10. 函数sin 2sin cos x y x x =-在区间π7π,412⎛⎤ ⎥⎝⎦上的最小值是 ． 二、解答题11. 函数2()cos cos f x x x x =-．〔1〕写出()f x 的单调增区间；〔2〕假设将()f x 的图象向右平移(0)ϕϕ>个单位，所得图象关于y 轴对称，求ϕ的最小值．12. 4tan 23α=-，sin cos ββ+，其中()π0,,0,π2αβ⎛⎫∈∈ ⎪⎝⎭． 〔1〕求tan α及tan β的值；〔2〕求()()sin cos αβαβ-+的值．13. 向量(cos ,sin )OM αα=，(cos ,sin )ON x x =，4(cos ,sin )5cos PQ x x α=-+.〔1〕当1cos 5sin xα=时，求函数y ON PQ =⋅的最大值； 〔2〕当1213OM ON ⋅=，OM PQ ， x α-，x α+都是锐角时，求cos2α的值. 14. 函数()π1sin cos cos 264f x x x x ⎛⎫=+-+ ⎪⎝⎭． 〔1〕假设将()f x 的图象向左平移(0)m m >个单位后，所得图象关于直线π12x =对称， 求m 的最小值； 〔2〕假设()0f x =05π0,12x ⎡⎤∈⎢⎥⎣⎦，求0π6f x ⎛⎫+ ⎪⎝⎭的值． 15. (,)2παπ∈，且sin()1210πα+=．〔1〕求sin(2)6πα+的值； 〔2〕求cos(2)6πα-的值． 16. 函数()()πsin (,0,0,0)2f x A x x A ωϕωϕ=+∈>><<R 的局部图象如下列图，P 是 图象的最高点，Q 为图象与x 轴的交点，O为坐标原点．假设4,OQ OP PQ === 〔1〕求函数()y f x =的解析式；〔2〕将函数()y f x =的图象向右平移2个单位后得到函数()y g x =的图象，当[]0,3x ∈时，求函数()()()h x f x g x =⋅的值域．。

桃城区第十四中学2021-2021学年高一数学下学期第七次综合测试试题一、选择题〔此题一共20道小题，每一小题5分，一共100分〕1.不等式21≥-x x 的解集为 ( )A. ),1[+∞-B.]1,(--∞C. )0,1[-D. ),0(]1,(+∞--∞ 2.)(,0成立的是不能则下列不等式若<<b aba ba Db a C B ba A )21()21.(||||.22.11.>>>>3.关于x 的不等式02<++c bx ax 的解集为⎭⎬⎫⎩⎨⎧->-<21,2|x x x 或，其中b a ,为实数，那么02>+-c bx ax 的解集为〔 〕A ⎪⎭⎫ ⎝⎛2,21B ⎪⎭⎫ ⎝⎛--21,2C ()⎪⎭⎫ ⎝⎛+∞-⋃-∞-,212,D ()+∞⋃⎪⎭⎫ ⎝⎛∞-,221,4.设,a b c d >>，那么以下不等式中一定成立的是〔 〕A ．a c b d ->-B ．ac bd >C ．a c b d +>+D ．a c b d ÷>÷5.,,a b c ∈R ，假设a b >，那么以下不等式成立的是 ( ) A.11a b< B. 22a b >C.2211a bc c >++ D. a c b c >6.假设关于x 的不等式m x x ≥-42对任意]1,0[∈x 恒成立，那么实数m 的取值范围是〔 〕 A.3-≤mB. 3-≥mC.03≤≤-mD.03≥-≤m m 或7.数列{a n }中，假设12a =，123n n a a +=+，那么10a =〔 〕A. 29B. 2557C. 2569D. 25638.我国古代著名的?周髀算经?中提到：凡八节二十四气，气损益九寸九分六分分之一；冬至晷〔guǐ〕长一丈三尺五寸，夏至晷长一尺六寸意思是：一年有二十四个节气，每相邻两个节气之间的日影长度差为1996分；且“冬至〞时日影长度最大，为1350分；“夏至〞时日影长度最小，为160分那么“立春〞时日影长度为A. 19533分B. 110522分C. 211513分D. 512506分9.等差数列{a n }的前n 项和为S n ，686a a +=，963S S -=，那么使S n 获得最大值时n 的值是( ) A. 5B. 6C. 7D. 810.等比数列{a n }的前n 项和为S n ，32110S a a =+，59a =，那么1a =〔 〕A.13B.19 C.13-D. 19-11.等差数列{a n }的前n 项和为S n .假设10305,10S S ==,那么40S =〔 〕A. 7B. 8C. 9D. 1012.等差数列{a n }的前n 项和为S n ，且244,16S S ==，数列{b n }满足1n n n b a a +=+，那么数列{b n }的前9项和9T 为 ( )A. 20B. 80C. 166D. 18013.等差数列{a n }的前n 项和为S n ，假设1785S =，那么7911a a a ++的值是A. 10B. 15C. 25D. 3014.数列{a n }满足712,83,8n n a n n a a n -⎧⎛⎫-+>⎪ ⎪=⎝⎭⎨⎪≤⎩，假设对于任意*n N ∈都有1n n a a +>，那么实数a的取值范围是〔 〕 A. 10,3⎛⎫ ⎪⎝⎭B. 10,2⎛⎫ ⎪⎝⎭C. 1(,1)2D. 11,32⎛⎫⎪⎝⎭15.数列{a n }是首项为12a =，公比2q的等比数列，且1n n n b a a +=+.假设数列{b n }的前n项和为S n ，那么S n =〔 〕 A. 323n ⋅- B. 1323n +⋅- C. 32n ⋅D. 1326n +⋅-16.数列{a n }满足()*+∈+==N n n a a a n n 11,1,那么4a 等于( )A. －7B.4C.7D.217.数列{a n }满足112a =，121n n a a n n +=++，那么a n =〔 〕A.312n - B. 321n -+ C. 111n -+ D.312n+ 18.数列{a n }的前n 项和122n n S +=-，那么22212n a a a +++=〔 〕A. 24(21)n- B 4(41)3n - C.. 124(21)n -+ D.14(42)3n -+19.等差数列{a n }，12018a =-，其前n 项和为S n ，20192018120192018S S -=，那么2019S =( )A. 0B. 1C. 2021D. 202120.对于数列{a n }，定义11222n nn a a a A n-+++=为数列{a n }的“好数〞，某数列{a n }的“好数〞12n n A +=，记数列{}n a kn -的前n 项和为S n ，假设6n S S ≤对任意的*n N ∈恒成立，那么实数k 的取值范围为〔 〕 A. 916[]47， B. 167[]73， C. 712[]35，D. 125[]52，二、填空题〔此题一共4道小题，每一小题5分，一共20分〕 21.数列{a n }的前n 项和满足()2*2n S n n n =-∈N ，那么4a=______．22.在如图的数表中，仅列出了前6行，照此排列规律还可以继续排列下去，那么数表中第n 〔n ≥3〕行左起第3个数为_______。