第十四届数学及应用能力竞赛试题

第十四届“中环杯”中学生思维能力训练活动初二年级决赛1.方程（x2-11x+1）（x2-11x+2）…（x2-11x+100）=0 的所有实数根的和为_____2.已知a、b、c＞0，且x满足，则x=______3.已知a=√￣3+√￣5+√￣7，b=√￣3-√￣5+√￣7，c=√￣3+√￣5-√￣7，计算：_______4.如图，△ABC的三边长度AB=7，BC=8，AC=9，点D在AC上，使得角CBD=45°，则BD=_____5.小钱、小王、小张、小孙、小陶都很喜欢运动，每人都喜欢羽毛球、排球和壁球中的一种或几种。

已知没有人三种运动都喜欢，但有人同时喜欢羽毛球和排球，也有人同时喜欢排球和壁球，还有人同时喜欢羽毛球和壁球。

那么五个人各自爱好的球类运动共有____种不同的组合方式。

6.已知一元三次方程x3-x-1=0有三个根，x1，x2，x3，则_______7.方程组的解为_____8.已知正整数n≤1000000，且（其中[x]表示不大于x的最大正整数）则满足条件的n有____个9.如图，在平行四边形ABCD中，BC边上恰好有8个点E1、E2、E3、…E i（图中只画出了3个点），满足B E1/BC=1/（i+1）（i=1、2、…8），比如B E1/BC=1/2，B E2/BC=1/3，…，B E2/BC=1/9，在AB边上有998个点G1、G2、…G998，这998个点将AB边平分成为999段。

我们从BC边上选取一个点E，从AB边上选取一个点G1（一共有8×998种选法），联接AE1并延长，交DC延长线于点F，联结FG1、FB，这么多选法中，使得10.如果一个正整数b（b≥2）满足以下的条件，我们就称其为“恒生银行数”，存在两个正整数x、y（0＜x＜b，0＜y＜b），使得x+y/b是x/y的整数倍，那么，小于等于100的“恒生银行数”一共有____个11.用2个1×2的小长方形可以拼成图1所示的图形，有两种拼法，如图2，图3（黑色小长方形和白色小长方形互换位置，视为同一种拼法），用11个1×2的小长方形七号拼成如下图形，那么共有多少种不同拼法？12.13.如图，D、E、F分别是△ABC中BC，CA，AB上的点，满足BD=CE=AF且角BDF=角CED=角AFE，求证：△ABC是一个等边三角形14.已知四个非负整数m、n、N、k满足方程（n2+1）2k·（44n3+11n2+10n+2）=N m，求证m=115.将图2中的10艘小船放入图1的表中，小船中的每一块占据一个方格，每艘船都是水平或竖直放置，并且任意两艘船不会相邻（如果一艘船中的某一格与另一艘船中的某一格相邻，就认为这两艘船相邻）表中右边和下面的数字表示这行，这列中小船占据的方格数量，游戏波浪线的地方表示这里不能放置船。

第14届数学竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 2.5B. √3C. 1/3D. 0.33333（无限循环）2. 已知函数f(x) = 2x^2 - 3x + 1，求f(x)的最小值。

A. -1B. -2C. -3D. 13. 一个圆的半径为5，求其面积。

A. 25πB. 50πC. 75πD. 100π4. 已知等差数列的首项a1=3，公差d=2，求第10项a10。

A. 23B. 25C. 27D. 295. 一个直角三角形的两条直角边分别为3和4，求斜边的长度。

A. 5B. 6C. 7D. 86. 已知一个点P(1,2)，求点P到原点O(0,0)的距离。

A. √2B. √5C. 2√2D. 3√27. 一个正方体的体积是27立方厘米，求其边长。

A. 3厘米B. 4厘米C. 5厘米D. 6厘米8. 已知一个等腰三角形的底边长为6厘米，两腰长为5厘米，求其面积。

A. 12平方厘米B. 15平方厘米C. 18平方厘米D. 20平方厘米9. 求下列数列的第10项：1, 1, 2, 3, 5, 8, ...A. 21B. 34C. 55D. 8910. 已知一个二次方程x^2 + 4x + 4 = 0，求其根。

A. x = -2B. x = -1, -3C. x = -2, -2D. 无实数根答案：1. B2. A3. B4. A5. A6. B7. A8. B9. C10. C二、填空题（每题4分，共20分）11. 一个数的平方根是4，这个数是_________。

12. 一个数的立方根是2，这个数是_________。

13. 将分数3/4化简为最简分数是_________。

14. 已知一个数列的前三项为2, 5, 11，求第四项。

15. 一个数的倒数是1/4，这个数是_________。

答案：11. 1612. 813. 3/414. 2315. 4三、解答题（每题10分，共50分）16. 证明勾股定理。

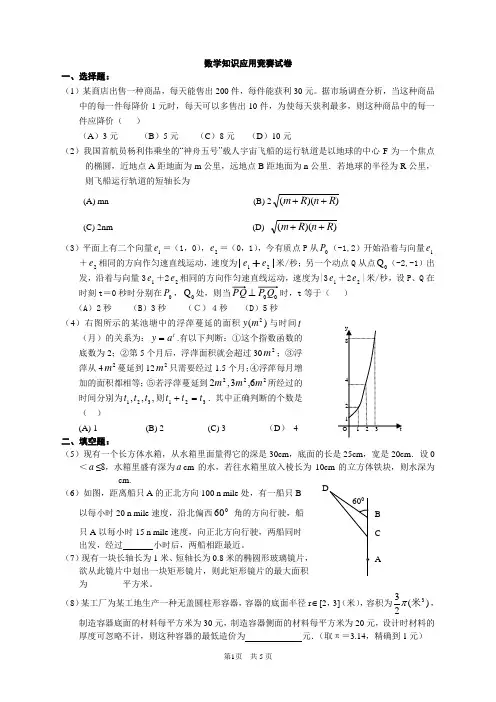
AC B 数学知识应用竞赛试卷一、选择题：（1）某商店出售一种商品，每天能售出200件，每件能获利30元。

据市场调查分析，当这种商品中的每一件每降价1元时，每天可以多售出10件，为使每天获利最多，则这种商品中的每一件应降价（ ）（A ）3元 （B ）5元 （C ）8元 （D ）10元（2）我国首航员杨利伟乘坐的“神舟五号”载人宇宙飞船的运行轨道是以地球的中心F 为一个焦点的椭圆，近地点A 距地面为m 公里，远地点B 距地面为n 公里．若地球的半径为R 公里，则飞船运行轨道的短轴长为(A) mn (B) 2))((R n R m ++ (C) 2nm (D)))((R n R m ++（3）平面上有二个向量1e ＝（1，0），2e ＝（0，1），今有质点P 从0P （-1,2）开始沿着与向量1e ＋2e 相同的方向作匀速直线运动，速度为|1e ＋2e |米/秒；另一个动点Q 从点0Q （-2,-1）出发，沿着与向量31e ＋22e 相同的方向作匀速直线运动，速度为|31e ＋22e |米/秒，设P 、Q 在时刻t ＝0秒时分别在0P ，0Q 处，则当00Q P ⊥时，t 等于（ ） （A ）2秒 （B ）3秒 （Ｃ）４秒 （D ）5秒 （4）右图所示的某池塘中的浮萍蔓延的面积)(2m y 与时间t（月）的关系为：ta y =.有以下判断：①这个指数函数的底数为2；②第5个月后，浮萍面积就会超过302m ；③浮萍从42m 蔓延到122m 只需要经过1.5个月；④浮萍每月增加的面积都相等；⑤若浮萍蔓延到22m ,226,3m m 所经过的时间分别为,,,321t t t 则321t t t =+．其中正确判断的个数是（ ）(A) 1 (B) 2 (C) 3 （D ） 4 二、填空题：（5）现有一个长方体水箱，从水箱里面量得它的深是30cm ，底面的长是25cm ，宽是20cm ．设0＜a ≤8，水箱里盛有深为a cm 的水，若往水箱里放入棱长为10cm 的立方体铁块，则水深为_________cm.（6）如图，距离船只A 的正北方向100 n mile 处，有一船只B以每小时20 n mile 速度，沿北偏西060 角的方向行驶，船 只A 以每小时15 n mile 速度，向正北方向行驶，两船同时 出发，经过 小时后，两船相距最近。

2014年第14届“中环杯”小学数学竞赛试卷（五年级初赛）一、简答题1．（2011•船营区校级自主招生）（1+）×（1﹣）×（1+）×（1﹣）×…×（1+）×（1﹣）2．最接近2013的质数是．3．黑箱中有60块大小、形状都相同的木块，每15块涂上相同的颜色，一次至少取出块才能保证期中至少有2块木块颜色相同．4．一共有52个学生参加游园活动，其中参观植物馆的有12人，参观动物馆的有26人，参观科技馆的有2人，既参观植物馆又参观动物馆的有5人，既参观植物馆又参观科技馆的有2人，既参观动物馆又参观科技馆的有4人，三个馆都参观的有1人，则有人这三个馆都没有参观．5．如图，∠B=30°，∠D=20°，∠A=60°，则∠BCD（图中有圆弧部分的那个角）的度数为°．6．一次考试中，小明需要计算37+31xa的值，结果他计算成了37+31+a．幸运的是，他仍然得到了正确的结果．则a=．7．某次射箭比赛，满分是10分，初赛阶段淘汰所有参赛者的50%．已知进入复赛的选手平均分比全体选手的平均分高2分，且进入复赛选手的平均分是8分．则被淘汰选手的平均分是分．8．有若干本书和若干本练习本．如果按每1本书配2本练习本分给一些学生，那么练习本分完时还剩2本书，如果按每3本书配5本练习本分给另一些学生，那么书分完时还剩1本练习本．那么，书有本，练习本有本．9．在51个连续奇数1、3、5、…101中选取k个数，使得它们的和为2013，那么k的最大值是．10．小明和小强玩了一个数字游戏，小明选择了一个数字x（0﹣9之间），然后说：“我正在考虑一个三位数（百位允许为0），这个三位数的百位为x，十位为3，并且能被11整除，请你找出这个三位数的个位数．”小强非常开心，因为他知道能被11整除的数的规律．但是他思考后发现这样的三位数不存在．则x=．11．我们将具有如下特性的四位数称为“中环数”：（1）四个数字各不相同；（2）千位数字既不是这四个数字中最大的，也不是这四个数字中最小的；（3）个位数字不是这四个数字中最小的．这样的“中环数”有个．12．世纪公园里有一片很大的草地，每天总会长出很多杂草（假设每分钟长出的杂草数量固定）．每天早上8点，一些工人会去除杂草（每个人的除杂草速度相同），一旦除完杂草（杂草的数量为0，好的草不会被除掉），工人们就收工了，之后长出的杂草留到明天再除．第一天，一些工人去除草，除到9点收工；第二天，10个工人去除草，除到8点30分收工；第三天，8个工人去除草，除到点分收工（最后分钟的值四舍五入，填一个整数即可）．13．如图，一个棱长为12厘米的正方体被切了一刀，这刀是沿IJ切入，从LK切出，使得AI=DL=4厘米，JF=KG=3厘米，截面IJKL为长方形．正方体被切成了两个部分，这两个部分的表面积之和为平方厘米．14．如图是一个除法算式．在空格中填入合适的数字能使这个算式成立．那么被除数是．15．A、B、C均为正整数．已知A有7个约数，B有6个约数，C有3个约数，AxB有24个约数，BxC有10个约数．则A+B+C的最小值为．16．有这样的正整数n，使得8n﹣7、18n﹣35均为完全平方数．则所有符合要求的正整数n=．17．将2013x1，2013x2，2013x3，2013x4，2013x5，2013x6，2013x7，2013x8，2013x9，2013x10，2013x11填入下表，使得填入的数能被其所在列的位置号整除，那么有18．如图，ABCD是长边为6的正方形，ADGH是一个梯形，点E、F分别是AD、GH的中点，HF=6，EF=4，EF⊥GH．联结HE并延长交CD于点I，作IJ⊥HA，则IJ=．19．如图，甲、乙两只蚂蚁在下列圆周上运动．AC为大圆的直径，点B在AC上，AB、BC分别为两个小圆的直径．甲蚂蚁在大圆上顺时针爬行，乙蚂蚁在两个小圆上沿着箭头所指方向绕“8”字爬行（A→B→C→B→A）．甲蚂蚁与乙蚂蚁在某一时刻同时从A点出发，然后不断爬行，速度为V甲：V乙=3：2．经过T1分钟，两只蚂蚁相遇．接下来，甲蚂蚁将自己的速度提高了，乙蚂蚁的速度不变，继续在原来的轨道上爬行．经过T2分钟，两只蚂蚁再一次相遇．已知T1+T2=1003﹣993+983﹣983+…+23﹣13，则甲蚂蚁按原来的速度绕大圈爬行一周需要分钟（本题答案写为假分数）．20．将0～9填入如图圆圈中，每个数字只能使用一次，使得，每条线段上的数字和都是13．2014年第14届“中环杯”小学数学竞赛试卷（五年级初赛）参考答案与试题解析一、简答题1．（2011•船营区校级自主招生）（1+）×（1﹣）×（1+）×（1﹣）×…×（1+）×（1﹣）【解答】解：（1+）×（1﹣）×（1+）×（1﹣）×…×（1+）×（1﹣）=（1﹣）×（1+）×（1﹣）×（1+）×…×（1﹣）×（1+），=×（××××…×）×，=×1×，=．2．最接近2013的质数是2011．【解答】解：最接近2013的质数是2011；故答案为：2011．3．黑箱中有60块大小、形状都相同的木块，每15块涂上相同的颜色，一次至少取出5块才能保证期中至少有2块木块颜色相同．【解答】解：60÷15=4（种）4+1=5（块）答：一次至少取出5块才能保证期中至少有2块木块颜色相同．故答案为：5．4．一共有52个学生参加游园活动，其中参观植物馆的有12人，参观动物馆的有26人，参观科技馆的有2人，既参观植物馆又参观动物馆的有5人，既参观植物馆又参观科技馆的有2人，既参观动物馆又参观科技馆的有4人，三个馆都参观的有1人，则有1人这三个馆都没有参观．【解答】解：12+26+23﹣5﹣2﹣4+1=51（人）52﹣51=1（人）答：有1人这三个馆都没有参观．故答案为：1．5．如图，∠B=30°，∠D=20°，∠A=60°，则∠BCD（图中有圆弧部分的那个角）的度数为250°．【解答】解：如图所示，延长BC交AD于点E，因为∠A=60°，∠B=30°，所以∠CED=∠A+∠B=60°+30°=90°，因为∠BCD小=∠CED+∠D=90°+20°=110°，∠BCD大=360°﹣110°=250°；故答案为：250°．6．一次考试中，小明需要计算37+31xa的值，结果他计算成了37+31+a．幸运的是，他仍然得到了正确的结果．则a=．【解答】解：根据题意，可知37+31×a=37+31+a所以31a=31+a31a﹣a=3130a=31a=．故答案为：．7．某次射箭比赛，满分是10分，初赛阶段淘汰所有参赛者的50%．已知进入复赛的选手平均分比全体选手的平均分高2分，且进入复赛选手的平均分是8分．则被淘汰选手的平均分是4分．【解答】解：设共有2n人，则进入复赛的选手为2n×50%=n人、被淘汰的选手也为2n﹣n=n 人；[（8﹣2）×2n﹣n×8]÷n=4n÷n=4（分）；答：被淘汰选手的平均分是4分．故答案为：4．8．有若干本书和若干本练习本．如果按每1本书配2本练习本分给一些学生，那么练习本分完时还剩2本书，如果按每3本书配5本练习本分给另一些学生，那么书分完时还剩1本练习本．那么，书有15本，练习本有26本．【解答】解：设有原来有学生X人，根据题意得（X+2）÷3=（2X﹣1）÷55X+10=6X﹣36X﹣5X=10+3X=1313×1+2=15（本）13×2=26（本）答：书有15本，练习本有26本．故答案为：15，26．9．在51个连续奇数1、3、5、…101中选取k个数，使得它们的和为2013，那么k的最大值是43．【解答】解：首先1，3，5…是首项为1，公差为2的等差数列，所以前n项和为n2，且442＜2013＜452，452=2025，为了让K最大，不能取大于第45项的数89，所以取n=45，而452﹣2013=12，则要在前45项里面减去几个数让这几个数的值为12，且要减去最少的数，因为前面的等差数的第n项为2n﹣1，当n=7时，第7项等于13，只要在减去第一项就可以满足题意思，则在45项的基础上只要减去第7项和第一项，则K=45﹣2=43．答：K最大值为43．故答案为：43．10．小明和小强玩了一个数字游戏，小明选择了一个数字x（0﹣9之间），然后说：“我正在考虑一个三位数（百位允许为0），这个三位数的百位为x，十位为3，并且能被11整除，请你找出这个三位数的个位数．”小强非常开心，因为他知道能被11整除的数的规律．但是他思考后发现这样的三位数不存在．则x=4．【解答】解：设这个三位数为x3y，若这个三位数能被11整除，则有x+y﹣3能被11整除，由题意可知，无论y为0至9这十个数字中的哪一个时，这个三位数都不能被11整除，即存在：1≤x+y﹣3≤10，即当y取0至9时，x+y﹣3依次对应为1至10，即：x+0﹣3=1，则x=4；故答案为：4．11．我们将具有如下特性的四位数称为“中环数”：（1）四个数字各不相同；（2）千位数字既不是这四个数字中最大的，也不是这四个数字中最小的；（3）个位数字不是这四个数字中最小的．这样的“中环数”有1680个．【解答】解：从0至9中任选4个不同的数字有=210种选法，设取出的四个数字为a＜b＜c＜d，由于a、d都不能排千位与个位，只有两个位置可选，下的b，c没有要求，依次有2、1个位置可选，则中环数共有210×2×2×2×1=1680个．故答案为：1680．12．世纪公园里有一片很大的草地，每天总会长出很多杂草（假设每分钟长出的杂草数量固定）．每天早上8点，一些工人会去除杂草（每个人的除杂草速度相同），一旦除完杂草（杂草的数量为0，好的草不会被除掉），工人们就收工了，之后长出的杂草留到明天再除．第一天，一些工人去除草，除到9点收工；第二天，10个工人去除草，除到8点30分收工；第三天，8个工人去除草，除到8点39分收工（最后分钟的值四舍五入，填一个整数即可）．【解答】解：从第一天9点时到第二天8点30分，草长了23小时30分钟，从第二天8点30分到第三天8点，草也长了23小时30分钟，即，23×60+30=1410（分钟）9时﹣8时30分=30分钟所以，1个工人1分钟可除草：1410÷10÷30=4.7（份）8×4.7=37.6（份）1410÷（37.6﹣1）≈39（分钟）第三天用了39分钟把草除干净，即第三天8点39分收工．答：第三天，8个工人去除草，除到8点39分收工．故答案为：8，39．13．如图，一个棱长为12厘米的正方体被切了一刀，这刀是沿IJ切入，从LK切出，使得AI=DL=4厘米，JF=KG=3厘米，截面IJKL为长方形．正方体被切成了两个部分，这两个部分的表面积之和为1176平方厘米．【解答】解：过点I向BF作垂线，交BF于点p，则Ip=12，pJ=12﹣4﹣3=5，根据勾股定理，IJ2=122+52=169，所以IJ=13，13×12=156（平方厘米），所以这两个部分的表面积之和为：12×12×6+156×2=864+312=1176（平方厘米）；答：这两个部分的表面积之和1176平方厘米．故答案为：1176．14．如图是一个除法算式．在空格中填入合适的数字能使这个算式成立．那么被除数是97539．【解答】解：由1、7、9可知c、d、e、f都为奇数，且c≠5，d、e、f互不相同．由d×abc为三位数，e×abc为四位数，f×abc为三位数，可知e为d、e、f中最大的一个，所以e≥5．若e=5，则e×abc的个位为5，不为7，所以e≠5．若e=7，则由e×的个位为7，可知c=1，此时由f×的个位为9，可知f=9，与e＞f矛盾，所以e≠7；若e=9，则由e×的个位为7，可知c=3，由d×的个位为1，可知d﹣7，由f×abc的个位为9，可知f=3．由7×≤999⇒≤142，由9×≥1000⇒≥112．所以，ABC=113或123．而113×793=89609，万位不为9，因此≠113．所以=123，被除数为：123×793=97539．故答案为：97539．15．A、B、C均为正整数．已知A有7个约数，B有6个约数，C有3个约数，AxB有24个约数，BxC有10个约数．则A+B+C的最小值为91．【解答】解：有7个约数的最小数是26=646=2×3，所以有6个约数的最小数是2×32=18AxB=26×2×32=27×32它约数的个数是（7+1）×（2+1）=24个．有3个约数的最小数是22=4BxC有10个约数，2×32×22=23×32，它约数的个数是（3+1）×（2+1）=12个，不合题意，所以有3个约数的最小数是32=9BxC有10个约数，2×32×32=2×34，它约数的个数是（1+1）×（4+1）=10个A+B+C=64+18+9=91答：A+B+C的最小值为91．故答案为：91．16．有这样的正整数n，使得8n﹣7、18n﹣35均为完全平方数．则所有符合要求的正整数n=22或2．【解答】解：设8n﹣7=a2…①，18n﹣35=b2…②，①×9得，72n﹣63=9a2…③，②×4=72n﹣140=4b2…④式，③代入④式，得到9a2﹣4b2=77，即（3a+2b）（3a﹣2b）=77，又77=1×77=7×11，即或，解得a=13或3，分别把a=13或3，代入①得，8n﹣7=169，或8n﹣7=9，8n=176，或8n=25解得：n=22，或n=2，所以n=22或n=22．故答案为：22或2．17．将2013x1，2013x2，2013x3，2013x4，2013x5，2013x6，2013x7，2013x8，2013x9，2013x10，2013x11填入下表，使得填入的数能被其所在列的位置号整除，那么有24种所以除了2013×1，2013×2，2013×3，2013×6，2013×9，2013×11这六个数可以互相交换位置，其余的2013×4，2013×5，2013×7，2013×8，2013×10必须填在4、5、7、8、10号下面，2013×2，2013×6可以填在2、6下面，有2种填法；9下面可以填2013×3，2013×9，有2种填法；剩下3个数可以随意填在1、3、11下面，有6种填法；共有：2×2×6=24（种）；答：有24种不同的填写方法．故答案为：24．18．如图，ABCD是长边为6的正方形，ADGH是一个梯形，点E、F分别是AD、GH的中点，HF=6，EF=4，EF⊥GH．联结HE并延长交CD于点I，作IJ⊥HA，则IJ= 3.6．【解答】解：如图作辅助线，由分析可知，AM⊥HF，AM⊥AD，则AM=EF=4；因为点E、F分别是AD、GH的中点，所以AE=HM=3，又HM∥AE，所以四边形AEMH是平行四边形，所以OA=AM=×4=2．因为AE=DE，∠AEO=∠DEI，∠OAE=∠IDE=90°，所以△OAE≌△IDE，所以DI=AO=2；在RT△AMH中，由勾股定理可得AH==5，同理可得：HE=2，EI=，所以HI=HE+EI=3；由S△HAE=AE•EF=AH×EN可得：×3×4=×5×EN，解之得，EN=2.4；因为∠ENJ=∠J=90°，∠NHE=∠JHI，所以△HNE∽△HJI，所以=，所以=，解得IJ=3.6．故答案为：3.6．19．如图，甲、乙两只蚂蚁在下列圆周上运动．AC为大圆的直径，点B在AC上，AB、BC分别为两个小圆的直径．甲蚂蚁在大圆上顺时针爬行，乙蚂蚁在两个小圆上沿着箭头所指方向绕“8”字爬行（A→B→C→B→A）．甲蚂蚁与乙蚂蚁在某一时刻同时从A点出发，然后不断爬行，速度为V甲：V乙=3：2．经过T1分钟，两只蚂蚁相遇．接下来，甲蚂蚁将自己的速度提高了，乙蚂蚁的速度不变，继续在原来的轨道上爬行．经过T2分钟，两只蚂蚁再一次相遇．已知T1+T2=1003﹣993+983﹣983+…+23﹣13，则甲蚂蚁按原来的速度绕大圈爬行一周需要分钟（本题答案写为假分数）．【解答】解：由于乙爬行一个8字路程为πAB+πBC=πAC，甲爬得一圈的路程是πAC，所以甲乙所行路程相等，则甲从A到C的路程与乙从A到C的路程相等．则原来V甲：V乙=3：2，所以第一次相遇时，甲爬了3圈，乙爬了2个8字．在A点相遇．甲将速度提高了后，V甲：V乙=3×（1+）：2=4：2，所以第二次遇时，甲爬了2圈，乙爬了1个8字．T1+T2=1003﹣993+983﹣983+…+23﹣13=（100﹣99）+（2﹣1）×1+1）=1002+992+…+22+12+100×99+…+2×1=+1002﹣100+982﹣98+…+22﹣2=338350+22×﹣（100+98+96+ (2)=338350+171700+2550=507500．所以在507500分钟中，乙爬了3个8字，用时分．由于一开始来V甲：V乙=3：2，则甲以初始速度爬行一周需要×=分钟．故答案为：．20．将0～9填入如图圆圈中，每个数字只能使用一次，使得，每条线段上的数字和都是13．【解答】解：如图，参与本试卷答题和审题的老师有：sdhwf；春暖花开；xuetao；齐敬孝；旭日芳草；lqt；admin；忘忧草；whgcn；晶优；duaizh（排名不分先后）菁优网2016年4月27日。

第十四届中学生数理化综合实践活动八年级数学应用知识展示试题（A卷）地区__________ 学校___________ 姓名__________ 信息卡号__________测试说明：1. 必须在答题纸上答卷，否则成绩无效；选择题的答案涂到答题纸对应题目的标号上，非选择题的答案书写在答题纸指定区域内.2. 请在答题纸和试卷上填写有效信息.考试时间为120分钟，满分120分.一、选择题（本大题共8小题，每小题6分，共48分，每题只有1个选项是正确的）1. 下面4个选项为北京冬奥会吉祥物设计方案，其中不属于轴对称图形的是（）.A. B. C. D.2022=（）.2. 2A. 0B. 1C. 2021D. 20223. 今年以来，猪肉价格波动较大，王阿姨和李阿姨在生活上精打细算，为了减少开支，王阿姨和李阿姨制定了不同的购肉策略，王阿姨每次买一样重量的肉，李阿姨每次买一样钱数的肉，某个周六、周日两位阿姨同时在同一个摊位上买肉，但这两天这个摊位的肉价不一样，则从这两次买肉的均价来看（）.A. 王阿姨更合适B. 李阿姨更合适C. 谁更合适与猪肉的变动价格有关D. 谁更合适与买猪肉的量有关4. 共享单车已经成为许多城市中的重要交通工具，在北京上班的李雷，周一到周五要骑共享单车在单位宿舍与办公室之间进行两个往返，每个单程用时10分钟；周末和节假日回家（连续假日时，只需往返一次），从宿舍到家单程骑行要50分钟.有W，Z，M，D四家共享单车公司，其收费规则如下表所示，其中，使用半小时为一次；使用不足半小时，按一次计费.如果不考虑押金和服务等因素，仅从用车付费的角度，且只使用一个公司的单车，则李雷在2021年2月26日（周五）到7月13日（周二）期间，用（）公司的共享单车最划算（注：清明、端午各有三天假期，五一有五天假期）.A. WB. ZC. MD. D5. For real numbers a and b ，the symbol {}min ,a b is defined as {},min ,,b a ba b a a b ≥⎧=⎨<⎩，for example{}min 2,11-=-. If the function of x is {}min 21,5y x x =--+，the maximum of this function is （ ）.A. 2B. 3C. 4D. 56. 根据国家统计局2021年1月数据显示，我国2020年规模以上工业企业主要财务指标如表所示，现有如下说法，正确的是（ ）.注：1. 经济类型分组之间存在交叉，故各经济类型企业数据之和大于总计.2. 本表部分指标存在总计不等于分项之和情况，是数据四舍五入所致，未做机械调整. A. 2020年7类规模以上工业企业营业收入的中位数为380009.5 B. 2020年7类规模以上工业企业营业成本的平均数超过100000亿元C. 2020年规模以上工业企业利润总额同比增长率最高的为外商及港澳台商投资企业D. 2020年规模以上工业企业营业成本同比增长最高的为外商及港澳台商投资企业7. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架，其中卷第九勾股中记载：“今有邑，东西七里，南北九里，各中开门.出东门一十五里有木.问出南门几何步而见木？”其算法为：东门南到城角的步数，乘南门东到城角的步数，乘积作被除数，以树距离东门的步数作除数，被除数除以除数得结果，即出南门x 里见到树，则11972215x ⎛⎫⎛⎫⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭=.若一小城，如图所示，出东门1200步有树，出南门750步能见到此树，则该小城周长的最小值为（ ）（注：1里=300步，且两个正数的和大于等于其积开方的两倍，当两数相等时取等号）.A.B. 里C.D. 里8. 如图，AD 为等腰ABC △的高，其中50ACB ∠=︒，AC BC =，E ，F 分别为线段AD ，AC 上的动点，且AE CF =，当BF CE +取得最小值时，AFB ∠的度数为（ ）A. 75︒B. 90︒C. 95︒D. 105︒二、填空题（本大题共4小题，每题8分，共32分）9. 如图，“中国天眼”是我国具有自主知识产权、世界最大单口径、最灵敏的球面射电望远镜，其反射面的形状为球冠（球冠是球面被平面所截后剩下的曲面，截得的圆为球冠的底，与截面垂直的球体直径被截得的部分为球冠的高），设球冠底的半径为r ，球冠的高为h ，球冠所在球的半径为R ，球冠底面圆周长为C ，球冠表面积2S Rh π=，当65000S π=，500C π=时，rR=__________.10. 如图，分别以Rt XYZ △的直角边和斜边为边向形外作正方形AXZF ，正方形BCYX ，正方形DEZY ，若直角边1YZ =，2XZ =，则六边形ABCDEF 的面积为__________.11. 已知a ，b ，c 分别是Rt ABC △的三条边长，c 为斜边长，90C ∠=︒，我们把关于x 的形如a by x c c =+的一次函数称为“勾股一次函数”.若点P ⎛- ⎝⎭在“勾股一次函数”的图象上，且Rt ABC △的面积是4，则c 的值是__________.12. 在平面直角坐标系中，已知点()3,0A ，()0,4B ，将BOA △绕点A 按顺时针方向旋转得CDA △，连接OD .当DOA OBA ∠=∠时，直线CD 的解析式为__________.三、解答题（本大题共3小题，共40分）13.（13分）2022年卡塔尔世界杯预选赛正在各大洲如火如荼地开展，在欧洲区预选赛中某小组某队踢完12场积了19分.（1）已知足球积分为胜一场积3分，平一场积1分，负一场积0分，则该队现在胜、负、平各几场？ （2）为了鼓励该队获得好成绩，该队的赞助商制定了一个奖励机制，每位球员胜一场获得15000欧元奖励，平一场获得7000欧元奖励，输球没有奖励，但每一场均奖励5000欧元出场费，则该队一位球员最多能获得多少报酬？14.（13分）问题背景：在ABC △中，已知AB ，BC ，AC 面积.小辉在答题时先建立一个正方形网格（每个小正方形边长为1），再在网格中画出格点ABC △（即ABC △三个顶点都在小正方形的顶点处），如图所示.这样不需求ABC △的高，而借用网格就能计算出它的面积.我们把上述求ABC △面积的方法叫做构图法.（1）若ABC △（0a >），请运用构图法求出ABC △的面积；（2）若ABC △0m >，0n >，且m n ≠），试运用构图法求出ABC △的面积；（3）已知a ，b 都是正数，3a b +=.15.（14分）问题的提出：如果点P 是锐角ABC △内一动点，如何确定一个位置，使点P 到ABC △的三顶点的距离之和PA PB PC ++的值为最小？ 问题的转化：（1）把APC △绕点A 逆时针旋转60︒得到''AP C △，连接'PP ，这样就把确定PA PB PC ++的最小值的问题转化成确定'''BP PP P C ++的最小值的问题了，请你利用图甲证明：'''PA PB PC BP PP P C ++=++.问题的解决：（2）当点P 到锐角ABC △的三顶点的距离之和PA PB PC ++的值为最小时，请你用一定的数量关系刻画此时点P 的位置__________. 问题的延伸：（3）图乙是有一个锐角为30︒的直角三角形，如果斜边为2，点P 是这个三角形内一动点，请你利用以上方法，求点P 到这个三角形各顶点的距离之和的最小值.初二数学答案一、选择题（每题6分，共48分） 1. C 2. C2202222022=22022=22022=22022=22022=2220222022120222021=+--=.3. B【解析】设王阿姨每次买肉量为x ，李阿姨每次卖肉价为y ，两次卖肉的单价分别为a ，b ，则王阿姨两次卖肉的均价为22ax bx a bx ++=，李阿姨两次卖肉的均价为22y ab y y a b a b=++且22()022()a b ab a b a b a b +--=≥++， 又a b ≠，所以2()02()a b a b ->+，即22a b aba b+>+， 所以这两次加油的均价，李阿姨的较低。

第十四届华罗庚金杯少年数学邀请赛初赛试卷（小学组）（时间：2009年3月14日 10：00～11：00）一、 选择题（每小题10分，满分60分. 以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内）第十四届华罗庚金杯少年数学邀请赛初赛10分1.下面的表情图片中，没有对称轴的个数为（ ）（A ） 3 (B ) 4 (C ) 5 (D ) 61.分析：通过观察可知，第1，2，5这三张图片是有对称轴的，其他的5张图片都没有对称轴，所以没有对称轴的个数为5，正确答案是C 。

第十四届华罗庚金杯少年数学邀请赛初赛10分2.开学前6天，小明还没做寒假数学作业，而小强已完成了60道题，开学时，两人都完成了数学作业. 在这6天中，小明做的题的数目是小强的3倍，他平均每天做（ ） 道题.（A ） 6 (B ) 9 (C ) 12 (D ) 152.分析：由于开学前6填时小强比小明多做了60道题，而开学时两人做的题一样多，所以这6填中小明比小强多做了60道题，而这6天中小明做的题的数目是小强的3倍，所以这6天小明做了60÷（3-1）×3=90道题，他平均每天做90÷6=15道题。

正确答案为D 。

第十四届华罗庚金杯少年数学邀请赛初赛10分3.按照中国篮球职业联赛组委会的规定，各队队员的号码可以选择的范围是0～55号，但选择两位数的号码时，每位数字均不能超过5. 那么，可供每支球队选择的号码共（ ）个 .（A ） 34 (B ) 35 (C ) 40 (D ) 563.分析：根据题意，可供选择的号码可以分为一位数和两位数两大类，其中一位数可以为0~9，有10种选择；两位数的十位可以为1~5，个位可以为0~5，根据乘法原理，两位数号码有5×6=30种选择。

所以可供选择的号码共有10+30=40种。

第十四届华罗庚金杯少年数学邀请赛初赛10分4.在19、197、2009这三个数中，质数的个数是（ ）.（A ） 0 (B ) 1 (C ) 2 (D ) 34.分析：19是常见的质数，197容易检验知也是质数，本题主要是考查2009这个数是否是质数。

2016年第十四届小学“希望杯”全国数学邀请赛试卷（五年级第1试）一、填空题（共20小题，每小题3分，满分60分）1．（3分）20.16×32+2.016×680=．2．（3分）小猫咪A、B、C、D、E、F排队依次从猫妈妈手中领鱼干，每只小猫咪每次领一条，领完后在道队尾继续排队领，直到鱼干发完．若猫妈妈有278条鱼干，则最后一个领到鱼干的小猫咪是．3．（3分）某房间内的一堵墙上挂有一面镜子，且这堵墙的对面有一块电子表，李明聪镜中看到电子表显示的时间如图所示，则此时的实际时间是．4．（3分）如果自然数a、b、c、d除以6都余4，则a+b+c+d除以3，所得的余数是．5．（3分）三位偶数A、B、C、D、E满足A＜B＜C＜D＜E，若A+B+C+D+E=4306，则A最小．6．（3分）将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是．（1步指每“加”或“减”一个数）7．（3分）如图，若每个小正方形的边长是2，则图中阴影部分的面积是．8．（3分）某商店的同种点心有大小两种包装礼盒，大盒85.6元一盒，内有点心32块，小盒46.8元一盒，内有点心15块，若王雷用654元买了9盒点心，则他可得点心块．9．（3分）如图，在梯形ABCD中，若AB=8，DC=10，S△AMD=10，S△BCM=15，则梯形ABCD的面积是．10．（3分）两个数的最大公约数和最小公倍数分别是3和135，求这两个数的差最小是．11．（3分）14袋糖果每袋的平均重量经四舍五入到小数点后第一位等于90.2克，已知每袋糖果的重量都是整数，则这14袋糖果的总重量是．12．（3分）从数字1，2，3，4，5中任意取4个组成四位数，则这些四位数的平均数是．13．（3分）某数学竞赛有10道题，规定每答对一题得5分，答错或不答扣2分．A、B两人各自答题，得分之和是58分，A比B多得14分，则A答对道题．14．（3分）如图，若长方形S长方形ABCD=60平方米，S长方形XYZR=4平方米，则四边形S四边形EFGH=平方米．15．（3分）有一个三位数A，在它的某位数字的前面添上小数点后得数B，若A ﹣B=478.8，则A=．16．（3分）商店里有若干个柚子和西瓜，其中西瓜个数是柚子个数的3倍．如果每天卖出30个西瓜和20个柚子，3天后，西瓜个数比柚子个数的4倍少26．则商店里原有个柚子．17．（3分）已知a、b、c是3个彼此不同的质数，若a+b×c=37，则a+b﹣c最大是．18．（3分）李双骑车以320米分钟的速度从A地驶向B地，途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车，15分钟后以原来骑车速度的1.5倍继续向前驶向B地，到达B地时，比预计时间多用17分钟，则李双推车步行的速度是米/分钟．19．（3分）如图，将一个等腰三角形ABC沿EF对折，顶点A与底边的中点D 重合，若△ABC的周长是16厘米，四边形BCEF的周长是10厘米，则BC=厘米．20．（3分）解放军战士在洪水不断冲毁大坝的过程中要修好大坝，若10人需45分钟，20人需要20分钟，则14人修好大坝需分钟．2016年第十四届小学“希望杯”全国数学邀请赛试卷（五年级第1试）参考答案与试题解析一、填空题（共20小题，每小题3分，满分60分）1．（3分）20.16×32+2.016×680=2016．【分析】把2.016×680变形为20.16×68，然后根据乘法的分配律简算即可．【解答】解：20.16×32+2.016×680=20.16×32+20.16×68=20.16×（32+68）=20.16×100=2016故答案为：2016．【点评】本题利用具体的算式考查了学生对于乘法分配律的理解．2．（3分）小猫咪A、B、C、D、E、F排队依次从猫妈妈手中领鱼干，每只小猫咪每次领一条，领完后在道队尾继续排队领，直到鱼干发完．若猫妈妈有278条鱼干，则最后一个领到鱼干的小猫咪是B．【分析】共有6只小猫咪，278÷6=46…2，容易得出答案．【解答】解：共有6只小猫咪，每发6条鱼重复出现，而278÷6=46…2，余数是2，则最后一个领到鱼干的小猫咪是B．故答案为：B．【点评】关键是找出周期，本题周期=6．3．（3分）某房间内的一堵墙上挂有一面镜子，且这堵墙的对面有一块电子表，李明聪镜中看到电子表显示的时间如图所示，则此时的实际时间是02：55．【分析】根据镜面对称的性质求解，在平面镜中的像与实际的实物，恰好左右或上下颠倒，关于镜面对称；据此解答即可．【解答】解：画图如下：所以，此时的实际时间是02：55．故答案为：02：55．【点评】本题考查了镜面对称知识，得到相应的对称轴是解答本题的关键，难点是作出相应的对称图形；注意2、5的关于竖直的一条直线的轴对称图形是5、2．4．（3分）如果自然数a、b、c、d除以6都余4，则a+b+c+d除以3，所得的余数是1．【分析】自然数a、b、c、d除以6都余4，则a、b、c、d都可以表示为6×整数+4，后面分析就简单了．【解答】解：因为自然数a、b、c、d除以6都余4，所以a、b、c、d都可以表示为：6×整数+4，四个这样的数的和是：6×整数+16，除以3余1，所得的余数是1．答案是1．【点评】能被6整除，一定能被3整除，只需要把四个余数加起来，看除以3余几，就是答案．5．（3分）三位偶数A、B、C、D、E满足A＜B＜C＜D＜E，若A+B+C+D+E=4306，则A最小326．【分析】最大的三位偶数是998，要使A最小，则要让其他的4个数（B、C、D、E）尽量最大，由于三位偶数A、B、C、D、E满足A＜B＜C＜D＜E，所以E 最大是998，D最大是996，C最大是994，B最大是992，用5个数的和4306减去B、C、D、E这4个数的和就是A的值；据此解答．【解答】解：最大的三位偶数是998，要满足A最小且A＜B＜C＜D＜E，则E最大是998，D最大是996，C最大是994，B最大是992，4306﹣（998+996+994+992）=4306﹣3980=326，所以此时A最小是326．故答案为：326．【点评】解答此题关键是明确最大的三位偶数是998，要使A最小，则要让其他的4个数（B、C、D、E）尽量最大．6．（3分）将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是151．（1步指每“加”或“减”一个数）【分析】加15，减12，加3，…，就相当于每一个计算周期运算3步，增加：15﹣12+3=6，则26÷3=8…2，即运算26步经过了8的计算周期，再加15，减12各一次，然后用100加上6×8，再加上15，再减去12即可．【解答】解：每一个计算周期运算3步，增加：15﹣12+3=6，则26÷3=8…2，所以，100+6×8+15﹣12=100+48+3=151答：得到的结果是151．故答案为：151．【点评】这一类问题一般要利用余数的知识来解答．这就要求我们对题目要仔细审题，判断其不断重复出现的规律，也就是找出循环的固定数，然后利用除法算式求出余数，最后根据余数得出正确的结果．7．（3分）如图，若每个小正方形的边长是2，则图中阴影部分的面积是72．【分析】可以将图中阴影部分的三角形进行剪切和拼接，变成都是小正方形组成的图形，最后再数出正方形的个数，即可求得阴影部分的面积．【解答】解：根据分析，如图，将阴影部分进行剪切和拼接后得：此时，图中阴影部分的小正方形个数为：18个，每个小正方形的面积为：2×2=4，故阴影部分的面积=18×4=72．故答案是：72．【点评】本题考查了剪切和拼接，突破点是：将阴影部分进行剪切和拼接，数出小正方形的个数，从而求得阴影部分的面积．8．（3分）某商店的同种点心有大小两种包装礼盒，大盒85.6元一盒，内有点心32块，小盒46.8元一盒，内有点心15块，若王雷用654元买了9盒点心，则他可得点心237块．【分析】设大合x 盒，小盒y 盒，依题意有方程：85.6x +46.8（9﹣x ）=654解方程可知大小各多少盒，进而可求出块数．【解答】设大合x 盒，小盒y 盒，依题意有方程：85.6x +46.8（9﹣x ）=654解方程得x=6，9﹣6=3．所以大合6盒，小盒3盒，共有32×6+15×3=237块．答：可得点心237块．【点评】本题如果用算术法求解，要用假设法．可先假设9盒全是15块一盒的，应花钱46.8×9=437.4元，比实际少232.8元，这是把其中的大合看成了小盒， 1大合看成了1小盒少算85.6﹣46.8=38.8元，大合有232.8÷38.8=6盒，小盒9﹣6=3盒．9．（3分）如图，在梯形ABCD 中，若AB=8，DC=10，S △AMD =10，S △BCM =15，则梯形ABCD 的面积是 45 ．【分析】△ADM 、△BCM 、△ABM 都等高，所以S △ABM ：（S △ADM +S △BCM ）=8：10=4：5，已知S △AMD =10，S △BCM =15，即可求出S △ABM 的面积，进而求出梯形ABCD 的面积．【解答】解：△ADM 、△BCM 、△ABM 都等高，所以S △ABM ：（S △ADM +S △BCM ）=8：10=4：5，已知S △AMD =10，S △BCM =15，所以S △ABM 的面积是：（10+15）×=20，梯形ABCD 的面积是：10+15+20=45；答：梯形ABCD 的面积是45．故答案为：45．【点评】本题关键是明确等高的三角形，面积比等于对应底的比．突破口是得到S△ABM：（S△ADM+S△BCM）=8：10．10．（3分）两个数的最大公约数和最小公倍数分别是3和135，求这两个数的差最小是12．【分析】首先要知道最大公约数和最小公倍数是如何求得的，最大公约数是两个数的公有质因数的积，最小公倍数是两个数的公有质因数和独有因数的积，所以用最小公倍数除以最大公约数就得到了两个数的独有因数的积，并且两个数的独有因数应该是互质的，然后根据质因数求出差最小的两个数即可．【解答】解：因为135÷3=45，45分解成两个互质的数有两种情况即1和45、9与5，所以差最小的是：9和5，所以这两个数分别是：9×3=275×3=1527﹣15=12答：这两个数的差最小是12．故答案为：12．【点评】本题考查了最大公因数和最小公倍数，解题关键是：最小公倍数除以最大公因数就得到了两个数的独有因数的积，并且两个数的独有因数应该是互质的．11．（3分）14袋糖果每袋的平均重量经四舍五入到小数点后第一位等于90.2克，已知每袋糖果的重量都是整数，则这14袋糖果的总重量是1263克．【分析】首先判断出这14袋糖果每袋的平均重量大于等于90.15和小于90.25之间，这14袋糖果的总重量大于或等于90.15×14=1262.1克和小于90.25×14=1263.5之间，然后求出这14袋糖果的总重量即可．【解答】解：用四舍五入取近似值的方法精确到一位小数能得到90.2的数值范围是：（大于等于90.15和小于90.25之间）所以这14袋糖果的总重量大于或等于90.15×14=1262.1克和小于90.25×14=1263.5之间，因为每袋糖果的重量都是整数，所以糖果的总重量也是整数，在1262.1和1263.5之间只有1263是整数，所以这14袋糖果的总重量是1263克．答：这14袋糖果的总重量是1263克．故答案为：1263克．【点评】解答此题的关键是判断出这14袋糖果每袋的平均重量大于等于90.15和小于90.25之间．12．（3分）从数字1，2，3，4，5中任意取4个组成四位数，则这些四位数的平均数是3333．【分析】千位上从5个数字有选择一个，就有5种选择的方法，百位上从剩下的4个数字中选择一个有4种不同的选择方法，十位上从剩下的3个数字中选择一个有3种选法，个位上从剩下的2个数字中选择一个有2种选法，它们的积就是全部的选择方法；5×4×3×2=120（种）；组成的四位数中，千位上是1的有24个数字，同理百位上是2，3，4，5的各有24个数字，十、个位上是1，2，3，4，5的也各有24个数字，即1，2，3，4，5在每个数位上各出现的24次，出现的次数相同，所以所有四位数的平均数的个位、十位、百位、千位都是1，2，3，4，5这5个数字的平均数．【解答】解：5×4×3×2=120（个），1×4×3×2=24（个），即1，2，3，4，5在每个数位上各出现的24次，可以组成120个不同的四位数；（1+2+3+4+5）÷5=3；那么平均数的各个位上的数字都是3，这个平均数就是3333．答：这些四位数的平均数是3333．故答案为：3333．【点评】根据乘法原理求出可以组成四位数的个数，再根据这些四位数的特点，找出它们的平均数．13．（3分）某数学竞赛有10道题，规定每答对一题得5分，答错或不答扣2分．A、B两人各自答题，得分之和是58分，A比B多得14分，则A答对8道题．【分析】因为得分之和是58分，A比B多得14分，根据和差公式可得A得了（58+14）÷2=36分，假设全部答对，则应得分为10×5=50分，则共相差50﹣36=14分，因为答错一道或不答和答对一道相差2+5=7分，所以答错14÷7=2道题．【解答】解：（58+14）÷2=72÷2=36（分）答错：（5×10﹣36）÷（2+5）=14÷7=2（道）答对：10﹣2=8道．故答案为：8．【点评】本题考查了和差问题与鸡兔同笼问题的综合应用，解答此类题的关键是用假设法，也可以用方程进行解答．14．（3分）如图，若长方形S长方形ABCD=60平方米，S长方形XYZR=4平方米，则四边形S四边形EFGH=32平方米．减去S 【分析】将图中面积相等的图形标出来，即等积变形，即长方形S长方形ABCD四边形后剩的八个三角形的面积可分成两半，一半再四边形EFGH中，长方形XYZR从而由此可以求得S．四边形EFGH【解答】解：根据分析，如下图所示：长方形S=S长方形XYZR+△AEF+△EFR+△FBG+△FGX+△HCG+△HGY+△DHE+△长方形ABCDHEZ=S长方形XYZR+2×（a+b+c+d）⇒60=4+2×（a+b+c+d）⇒a+b+c+d=28=△EFR+△FGX+△HGY+△HEZ+S长方形XYZR四边形S四边形EFGH=a+b+c+d+S长方形XYZR=28+4=32（平方米）．故答案是：32．【点评】本题考查了等积变形，本题突破点是：利用等积变形，将四边形的面积分割成四个三角和一个长方形，最后求和．15．（3分）有一个三位数A，在它的某位数字的前面添上小数点后得数B，若A ﹣B=478.8，则A=532．【分析】A﹣B=478.8，差是一位小数，说明B也是一位小数，原来的三位数A 变成一位小数就缩小了10倍，也就是A﹣B的差是B的9倍，用478.8除以9即可求出B，再把B的小数点向右移动一位就是A．【解答】解：A﹣B=478.8，则：B是A缩小10倍得到的478.8÷（10﹣1）=478.8÷9=53.2那么A=53.2×10=532．故答案为：532．【点评】此题应认真分析，通过观察数字得出：小数点，必在十位和个位之间，再根据差倍公式求解即可．16．（3分）商店里有若干个柚子和西瓜，其中西瓜个数是柚子个数的3倍．如果每天卖出30个西瓜和20个柚子，3天后，西瓜个数比柚子个数的4倍少26．则商店里原有176个柚子．【分析】首先找到题中的等量关系，表示出所有的数量列方程即可．【解答】解：依题意可知：3天后卖出90个西瓜和60个柚子．数量差为30个．设后来柚子是x个，西瓜是4x﹣26个．那么原来柚子是x+60个，原来西瓜是4x ﹣26+90；4x+90﹣26=3（x+60），x=116．故答案为：176【点评】本题的考查差倍问题的理解和运用，方程比较简单容易理解，问题解决．17．（3分）已知a、b、c是3个彼此不同的质数，若a+b×c=37，则a+b﹣c最大是32．【分析】要使a+b﹣c的值最大，就要使c的值最小，最小的质数是2，所以c=2；则可得：a=37﹣b×c=37﹣2b，然后再使b最小即可．当b=3时，a+3×2=37，a=31正好a、b、c都是质数将其分别代入a+b﹣c，得32【解答】解：要使a+b﹣c的值最大，就要使c的值最小，最小的质数是2，所以c=2；则可得：a=37﹣b×c=37﹣2b，要使a最大，则使b最小，b最小是3，所以，a最大是：a=37﹣2×3=31，所以，a+b﹣c最大是：a+b﹣c=31+3﹣2=32；答：a+b﹣c最大是32．故答案为：32．【点评】本题解答的突破口是先确定减数c=2，然后根据：因为b在与c的乘积中，所以只有使b尽量的小，才能保证a尽量的大解答即可．18．（3分）李双骑车以320米分钟的速度从A地驶向B地，途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车，15分钟后以原来骑车速度的1.5倍继续向前驶向B地，到达B地时，比预计时间多用17分钟，则李双推车步行的速度是72米/分钟．【分析】首先把李双原来骑车的速度看作单位“1”，用李双原来骑车的速度乘1.5，求出修完车后李双骑车的速度是多少；然后根据路程÷速度=时间，分别用1800除以修车前后李双骑车的速度，求出修车前后李双骑1800米用的时间各是多少，再用修车前李双骑1800米用的时间减去修车后李双骑1800米用的时间，求出修车后李双骑1800米少用多少分钟；最后用李双到达B地比预计多用的时间减去15，再加上修车后李双骑1800米少用的时间，求出李双步行5分钟的路程比同样的路程骑车用的时间多几分钟，再用李双骑车的速度乘李双步行5分钟的路程，骑车需要的时间，求出李双步行的路程是多少，再用它除以5，求出李双推车步行的速度是多少即可．【解答】解：1800÷320﹣1800÷（320×1.5）=5.625﹣3.75=1.875（分钟）320×[5﹣（17﹣15+1.875）]÷5=320×[5﹣3.875]÷5=320×1.125÷5=360÷5=72（米/分钟）答：李双推车步行的速度是72米/分钟．故答案为：72．【点评】此题主要考查了行程问题中速度、时间和路程的关系：速度×时间=路程，路程÷时间=速度，路程÷速度=时间，要熟练掌握，解答此题的关键是求出李双步行5分钟的路程比同样的路程骑车用的时间多几分钟．19．（3分）如图，将一个等腰三角形ABC沿EF对折，顶点A与底边的中点D 重合，若△ABC的周长是16厘米，四边形BCEF的周长是10厘米，则BC=2厘米．【分析】△ABC 的周长是16 厘米，因为△ABC 是等腰三角形，且顶点A与底边的中点D重合，所以△AEF 的周长等于△ABC 的周长的一半；可得△AEF 的周长为16÷2=8 （厘米），△AEF 和四边形BCEF周长和为8+10=18（厘米），18厘米正好比△ABC的周长是16厘米多了两条EF的长度，所以EF=（18﹣16）÷2=1 （厘米），又因为EF是中位线；则BC=2 EF=2（厘米）．【解答】解：△ABC的周长是16厘米，可得△AEF的周长为：16÷2=8 （厘米），△AEF 和四边形BCEF周长和为：8+10=18（厘米），所以BC=18﹣16=2（厘米），答：BC=2厘米．故答案为：2．【点评】本题关键是根据和差公式以及中位线的性质求出EF的长度，再进一步求出BC的长度．20．（3分）解放军战士在洪水不断冲毁大坝的过程中要修好大坝，若10人需45分钟，20人需要20分钟，则14人修好大坝需30分钟．【分析】假设每人每分钟修大坝1份，先求出洪水冲毁大坝速度：（10×45﹣20×20）÷（45﹣20）=2（份）；然后求出大坝原有的份数45×10﹣2×45=360（份）；再让14人中的2人修冲毁大坝的份数，剩下的14﹣2=12人修原有的360份，可求出需要的时间，据此解答．【解答】解：假设每人每分钟修大坝1份洪水冲毁大坝速度：（10×45﹣20×20）÷（45﹣20）=（450﹣400）÷25=50÷25=2（份）大坝原有的份数45×10﹣2×45=450﹣90=360（份）14人修好大坝需要的时间360÷（14﹣2）=360÷12=30（分钟）答：14人修好大坝需30分钟．故答案为：30．【点评】牛吃草的问题关键的是求出青草的生长速度和草地原有的草的份数．。

a
b
c 题图13
d
e
利用对称的性质，如图 2 和图 3 所示，蓝边等边三角形的面积是： 是 7 的等边三角形有 2×4×2=16 个； 利用对称性的性质，如图 4，黄色等边三角形的面积是 示，灰色难道正三角形的面积为
1 ×4×3+1=7,面积 2
1 ×24=12 的有 2 个。如图 5 所 2
1 ×6×3+4=13，面积为 13 的正三角形共有 4 个。 2
11．已知 a，b，c 是三个自然数，且 a 与 b 的最小公倍数是 60，a 与 c 的最小公 倍数是 270。求ｂ与ｃ的最小公倍数。 12．在 51 个连续的奇数 1，3，5，„，101 中选取 k 个数，使得他们的和为 1949， 那么 k 的最大值是多少？
三、 解答下列各题 （每小题 15 分， 共 30 分， 要求写出详细解答过程）
8．已知 1＋2＋3＋„„＋n(n﹥2)的和的个位数为 3，十位数为 0，则 n 的最小值 为__________。
二、解答下列各题（每题 10 分，共 40 分，要求写出简要过程）
1 1 1 1 1 1 9．六个分数 ， ， ， ， ， 的和在哪两个连续自然数之间？ 2 3 5 7 11 13
10．2009 年的元旦是星期四，问：在 2009 年，哪几个月的第一天也是星期四？ 哪几个月有 5 个星期日？
a，b 一定是 2
2
的倍数，但是 a,2
的倍数，所以 b 是 2
2
的倍数，
同理可得 c 是 3 的倍数，所以 b, c 应被 2 2 .3 整除。
3
3
因为 a , b =60， a , c =270,所以 60 是 b 的倍数，270 是 c 的倍数，

第十四届北京高中数学知识应用竞赛初赛试题及参考解答一、（满分20分）我们常常会发现在商店里买同一种商品，大包装的比小包装的合算。

如某种品牌的牙膏，质量30克的每支2.50元/支，质量120克的每支8.50元。

如果不考虑运输成本，假设一支牙膏的价格=（牙膏的生产成本＋包装成本）（1＋固定比例的商业利润率），而生产成本与商品的重量成正比，包装成本与商品包装的表面积成正比，商业的固定利润率为20%。

（1）分析下面的结果有何不妥：设220克牙膏的合理价格为x 元，于是有220120120308.508.50 2.50x −−=−−解得：x =15.17（元）（2）请你给出一种方式，计算出一支220克的这种牙膏的合理价格.（3）给出该商品的单位质量的价格C 与质量M 的关系，说明当M 增加时C 会减少。

（4）到市场上做一个调查，对照（2）中的方式，看看是否符合实际，若不符合，请给出适当的分析。

解：（1）问题在于，求解用的是线性模型，价格11152y x =+，其中x 是牙膏的质量（克）。

这样把牙膏的生产成本和包装成本等同地看成了x 的一次函数，随着x 的增加而等幅度的增加。

这与题目中“包装成本与商品包装的表面积成正比”不符合。

（2）可以将不同规格但同种的商品外包装看作是相似的，由题设，商品的价格=1.2×（牙膏的生产成本＋包装成本）；又，生产成本∝商品的质量M ，包装成本∝商品的表面积S ，商品的体积V ∝M 。

于是S ∝23V ∝23M 。

可设：合理价格y =a ×M +b ×23M ，其中a ，b 是待定系数。

由同种商品的两种规格的已知价格可定出a ，b ，于是解方程组23233030 2.501201208.50a b a b ⎧+=⎪⎨⎪+=⎩得a ≈0.05，b ≈0.1，于是y =0.05×M +0.1×23M 。

取M =220时得：y =14.64(元)，这是我们所要的结果，也就是220克的同种牙膏售价14.64元。

少年一组一、填空题1、115 解题思路：以21作为参照数，其中231116和305153均大于21，其余三个数115、136、6430均小于21。

用21与这三个数分别作差依次可得221、261、321。

所以，最小的数为115。

2、24解题思路：由ABCD 是正方形可得：ABCD DMC ADN S S S 21==∆∆。

根据容斥原理可得：RNC MQ NB APM D PQ R S S S S ∆∆∆++=,所以：24121551=--=∆MQ NB S 。

3、4种解题思路：105是一个奇数，所以这个数一定能写成2个相邻的自然数之和，即105＝52＋53。

又因为奇数个连续自然数数列的平均数等于这组数的中位数，根据105＝3×35＝5×21＝7×15，可以等到符合条件的三种表达式，分别是105＝34＋35＋36＝19＋20＋21＋22＋23＝12＋13＋14＋15＋16＋17＋18。

4、10110，99920解题思路：要使A 为能被5整除的五位数，则A 的各位必须是0或5。

当A 最小时，它的最高位只能是1，考虑到这个多位数均由奇数组成，因此可以在101与103之间截出一个最小的五位数是10110；当A 最大时，它的最高位上的数要尽可能大，故这个多位数中1999与2001之间可以截出一个最大的五位数时99920。

二、解答题5、解：由题意可得， 当110〈⎥⎦⎤⎢⎣⎡n 时，不存在符合题意的解，所以1～9均不是牛数。

当110=⎥⎦⎤⎢⎣⎡n 时，由于1是所有非0自然数的公因数，所以10～19都是牛数。

当210=⎥⎦⎤⎢⎣⎡n 时，n 必须是偶数才能符合题意，故在20～29之间符合条件的牛数只有20、22、24、26、28。

当310=⎥⎦⎤⎢⎣⎡n 时，n 必须是2和3的公倍数才能符合题意，故在30～39之间符合条件的牛数只有30、36。

当410=⎥⎦⎤⎢⎣⎡n 时，n 必须是3和4的公倍数才能符合题意，故在40～49之间符合条件的牛数只有48。

点作为评判参考： 1）学生能编出程序且运行正确，可得A级分数； 2）学生不能编出程序但算法正确，可得B级分数； 3）学生不能编出程序且算法错误，可得C级分数。
6
© Copyright 2012 Hewlett-Packard Development Company, L.P. The information contained herein is subject to change without notice.
全国中小学信息技术创新与实践活动 Network Originality Competition
“应用数学赛项“
NOC-初中组竞赛题
1.编程
请你用HP Prime设计程序，求出1000以内所+1
n是否为素数 是
将n值添加进列表L1
r>=1000 是
输出L1
结束
程序：
EXPORT 素数() BEGIN LOCAL n,k,L1:=2; FOR n FROM 3 TO 1000 DO FOR k FROM 2 TO n-1 DO IF n MOD k ==0 THEN BREAK; END; IF k==n-1 THEN L1:=CONCAT(L1,n); END; END; END; PRINT(L1); END;
结果：
13
© Copyright 2012 Hewlett-Packard Development Company, L.P. The information contained herein is subject to change without notice.
3. 本题考查学生的逻辑思维能力，创新能力及对计算器的熟练程度，可从以 下几点作为评判参考：
2.图案设计 请同学们在高级绘图应用程序中，逐项输入下列数学表达式并观察每个图象： 1） x0； 2）y 0 ；

最新全国数学竞赛试题及答案2019年全国高中数学联合竞赛一试(A卷) 参考答案及评分标准说明:1.评阅试卷时，请依据本评分标准.填空题只设8分和0分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不得增加其他中间档次.2.如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中第9小题4分为一个档次，第10、11小题5分为一个档次，不得增加其他中间档次.一、填空题：本大题共8小题，每小题8分，满分64分.1.已知正实数a满足/= (9〃广，则10gd(女r)的值为.答案：—.16। 2 Q解：由条件知9a = ，故初=《9a a ,所以log,(3。

)=布.2.若实数集合{1,2,3,*的最大元索与最小元素之差等于该集合的所有元素之和，则x的值为________________ .答案：一g.解:假如*20,则最大、最小元素之差不超过max{3,R,而所有元素之和大于nm{3,M，不符合条件.故xV0,即工为最小元索.「•是3 — x = 6 + x,解得”一二3. '『而直角坐标系中，c是单位向吊,向量。

满足a.c=2 ,旦(/ <5 t/4-Ze对任意实数/成立，则同的取值范围是.答案：[石,2石].解：不妨设e = (l,0).由于。

e = 2,可设。

=(2,$),则对任意实数/,有4-|-5: =a <5 a^-te = 5j(2 + /> +s],这等价于4 + $”5卜I，解得即于是a = j4 + s> 技2⑹.4.设43为椭圆「的长轴顶点，£/为「的两个焦点，卜川=4, |"| = 2 +百尸为「上•点，满足伊用.户”| = 2,则△〃//的面积为.答案：1.解：不妨设平而走角坐标系中「的标准方程为W + E=l(«>〃>0).a'根据条件得2a = [4 闿=4, a 土 J a? — b? =|/?] = 2 + 6，可知° = 2, Z> = 1,口闭=277H=26 猛磁懒锚由椭IM定义知+ p目=2。

广东第二师范学院第三届数学建模竞赛试题及参考解答一、最大收益某食品厂生产Ⅰ型和Ⅱ型饼干.在每种饼干的生产过程中，都需要使用搅拌机（A ）、成型机（B ）和烘箱（C ）三种设备.已知每生产一吨Ⅰ型饼干需要在A 、B 、C 上工作的时间分别为4、5、8小时.对Ⅱ型饼干，相应的时间为6、4、3小时.每生产一吨Ⅰ、Ⅱ型饼干均可获得利润7百元.这些饼干在市场上都很畅销.但由于条件限制，A 、B 、C 每天可供利用的工时不能超过24、20、24小时，试问应如何安排每天Ⅰ、Ⅱ型饼干的生产量，才能使该厂获得最大的收益？解：设每天Ⅰ、Ⅱ型饼干的生产量分别为12,x x 吨，每天的利润为Z ，则此问题的数学模型为：12maxZ 77x x =+s.t.12121212462454208324,0x x x x x x x x +≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ ------（10分）这是一个整线性规划问题，现用图解法进行求解可行域为：由直线112:4624l x x +=，212:5420l x x +=，312:8324l x x +=以及0,0x y ==组成的凸五边形区域.直线12:77l x x c +=在可行域内平行移动.------（18分） 易知：当l 过1l 与2l 的交点时，Z 取最大值.由121246245420x x x x +=⎧⎨+=⎩ 解得12127207x x =⎧⎨=⎩此时 max 1220773277Z =⨯+⨯=(百元). ------（25分） 故每天生产Ⅰ型饼干127吨，Ⅱ型饼干207吨，相应的收益最大是3200元.二、快件派送如图，快递员从C 3骑车出发往A 2、C 1、E 2三处送快件，然后回到C 3.图中数字单位为hm (百米)，假设车速为15km/h ，送快件时每处耽误5min ，试为快递员设计一条最短路线.问从出发算起30min 内该快递员能否回到出发地点？解：第一步：先找出C 3到达A 2、C 1、E 2各点间最短距离如下表：(单位hm) 从 到C 3 A 2 C 1 E 2C 3 0 9 8 10 A 2 9 0 11 16 C 18 11 0 8 E 210168-------------（10分）第二步：将第一步中表格转化为各地点间的加权无向图G(见下图)1.C 3；2.A 2；3.C 1；4.E 2图 各点间加权无向图 ------（17分）第三步，按最优邻近法求最佳线路的具体过程如下：16①开始于顶点1，组成闭回路11，在下一阶段最邻近1的顶点为顶点3，建立闭回路131，顶点4最邻近顶点3，建立闭回路1341.②将顶点2插入上面闭回路，得到6个闭回路是13421、13241、14321、14231、12341、12431，它们的长度分别为41、45、38、45、38、41.在这些闭回路中长度最短的回路14321、12341为最佳线路，即C 3—A 2—C 1 —E 2—C 3或C 3—E 2—C 1—A 2—C 3，距离均为3800m.按所给数据，骑车和派件耽误时间共2.303560150003800=⨯+⨯ (min)故从出发算起半小时内该快递员不能回到出发地点. ------（25分）三、雪球融化设雪球在融化时体积的变化率与表面积成比例，且在融化过程中它始终为球体，该雪球在开始时的半径为6cm ，经过2小时后，其半径缩小为3cm ，试推导雪球的体积随时间变化的关系式，并求3个小时后雪球的体积.解：设t 时刻雪球的体积为()v t ,表面积为s(t),则)()(t ks dtt dv -=，--（10分） 根据球体的体积(v =334R π)和表面积(s=4R π2=32)43(4ππv )的关系得s(t)=3232313)4(v π，引入新常数 r =k 32313)4(π，再利用题中的条件得32rv dtdv-=,v(0)=288π,v(2)=36π， --------------------（15分） 分离变量积分得方程的通解为 v(t)=271(c －rt)3---------------（20分） 利用条件v(0)=288π和v(2)=36π得c=3636π，r=936π.代入得雪球体积随时间变化的关系式为 v(t)=3)312(6t -π（实际问题要求t ∈[0,4]）. 3个小时后雪球的体积为：v (3)=92π. --------------（25分）四、宠物食谱一名兽医推荐宠物狗每天的食谱中应该包含100个单位的蛋白质，200个单位的卡路里，50个单位的脂肪.一个商店的宠物食物部有4种食物，分别为A 、B 、C 、D.每千克食物所含的营养成分如下：若单从该商店的这四种食物中取材，是否存在某种方案满足兽医推荐的食谱？解：此问题是对食物A 、B 、C 、D 进行混合，使得混合物中各种营养成分的含量与兽医推荐的量相等，故可列出线性方程组对此问题进行求解.设宠物狗一天食谱中食物A 、B 、C 、D 的量分别为1x 、2x 、3x 、4x （千克）.为保证其食谱满足兽医的推荐，可得如下线性方程组：1234123412345471010020251052002210650x x x x x x x x x x x x +++=⎧⎪+++=⎨⎪+++=⎩.---------（10分）同解方程组为：1234234345325181160361685x x x x x x x x x +++=⎧⎪--=-⎨⎪+=⎩.----------（15分）通过回代的方法确定上述方程组的非负解（实际问题的需要）.令4x t =，则0t ≥.于是，31(8516)036x t =-≥，此时要求8516t ≤.----（20分） 将4x 与3x 回代，求得235302x t =-≥，此时要求356t ≥. 然而1685635>, 故3585616t ≤≤无解.这就说明，不可能找到方程组的非负解，也即，该商店中的这四种食物无论如何配比，都不能完成兽医的配方要求. --------（25分）五、最优生产甲车间为乙车间生产某种原料，已知乙车间平均每月需要100件，而甲车间平均每月生产500件，因此甲车间要进行等周期分批有间断的生产. 另外甲车间的产品运到乙车间时要包装，平均每批的包装费为4元. 若运到乙车间后暂时来不及加工，则要花费存贮费，平均每件每月0.4元，每月按30天计算，请通过建立数学模型给出甲车间的最优生产周期. (注：据调查知在一个生产周期T 天的存贮费用为01()2P R TT C -，其中0=RT T P为生产时间，P 为甲车间的生产速度，R 为乙车间的需求速度，C 为每天每件产品的存贮费.) 解：设一个生产周期T 天的包装费为D ，每个月生产的批数为30/T ，因此每个月内的总费用()F T 为0301()()2130()2F T D P R TT C T D R P R TC T P ⎛⎫=+- ⎪⎝⎭⎛⎫=+- ⎪⎝⎭------------------（10分）利用微积分求极值方法可得21()3002D P R F T RC T P -⎛⎫'=-+= ⎪⎝⎭从而T =-------------（15分）已知：P =500/30，R =100/30，D =4，C =0.4/30，于是可得15T ===因此，甲车间的最优生产策略为每隔15天生产一批. ----------（25分）六、鱼雷轨迹位于坐标原点的我舰向位于x 轴上距离我舰1公里处的敌舰发射制导鱼雷．假设敌舰以速度0v 沿着平行于y 轴的直线行进，鱼雷始终对准敌舰且速度为02v . 请建立数学模型确定鱼雷的轨迹方程.解：设鱼雷航行轨迹方程为()y y x =. 在时刻t 鱼雷的坐标为(,)P x y ，敌舰的坐标为0(1,)Q v t . 因鱼雷始终对准敌舰，所以有01v t yy x-'=- (1) ----------（5分） 而弧线»OP的长度为002=⎰v t (2) ----------（8分）由(1)、(2)两式消去0v t 得(1)x y ''-=（12分） 根据题意，初始条件为(0)0,(0)0y y '== 令y p '=，方程(3)化为(1)x p '-=由方程(4)解得121(1)y C x -'=- (5) ----------（17分）将(0)0y '=代入(5)式得11C =，所以12(1)y x -'=-，又由12(1)y x '==-，于是11221(1)(1)2y x x -⎛⎫'=--- ⎪⎝⎭(6) ----------（22分）积分得312221(1)(1)3y x x C =---+ (7)将(0)0y =代入(7)式得223C =，所以鱼雷的航行轨迹方程为 312212(1)(1)33y x x =---+． ----------（25分）。

第十四届华罗庚金杯少年数学邀请赛决赛试题C参考答案(小学组)9．答案：在1和2之间．解答：11111123571113+++++=111111()()()21331157+++++=151412 263335++因为151412151412412 26333526262626 ++<++=<，又因为151412151412411 26333535353535 ++>++=>所以六个分数111111,,,,,23571113的和在1和2之间．10．答案：10月份的第一天是星期四，3、5、8、11月有五个星期日．解答：下表列出各个月的1号的相关信息．10月1号与l月1号相距273天，273是7的倍数，所以，10月份的第一天也是星期四．3月1号是星期日，3月份有31天，所以3月有5个星期日；5月3号是星期日，5月份有31天，所以5月有5个星期日；8月2号是星期日，8月份有31天，所以8月有5个星期日；11月1号是星期日，11月份有30天，所以11月有5个星期日．11．答案：540或l08．解答：如果b 不22的倍数，因为2[,]235a b =⨯⨯，则a 一定是22的倍数．由此可知[,]a c 一定是22的倍数．但是2[,]235a c =⨯⨯不是22的倍数．所以b 是22的倍数．同理可得c 是23的倍数．所以[,]b c 应被2223⨯整除．因为[,]60a b =，[,]270a c =，所以60是b 的倍数，270是c 的倍数． 所以b ，c 的最小公倍数[b ，c]是[60，270]的约数． 因为[60，270]=22·33·5，所以[b ，c]= 22·33·5=540或[b ，c]= 22·33=108．当a=1，b=60，c=270时，[a ，c]=60，[a ，c]=270，[b ，c]=540； 当a=5，b=12，c=54时，[a ，c]=60，[a ，c]=270，[b ，c]=108． 12．答案：l00．解答：面积是l 的等边三角形有32个；面积是4的等边三角形有18个；面积是9的等边三角形有8个；面积是16的等边三角形有2个；利用对称的性质，如图l ，红色等边三角形的面积是由6个面积是l 的等边三角形组成的正六边形面积的一半，等于3；面积是3的等边形角形共有9×2=18个；利用对称的性质，如图2和图3所示，蓝色等边三角形的面积是：143172⨯⨯+=，面积是7的等边三角形共有2×4×2=16个；利用对称性的性质，如图4，黄色等边三角形的面积是124122⨯=的有2个．如图5所示，灰色的正三角形的面积为1634132⨯⨯+=，面积为13的正三角形共有4个．因此，可以连成的等边三角形总计有：321882181624100+++++++=(个)．三、解答下列各题 (每小题15分，共30分，要求写出详细过程)1图图2图3图4图513．答案：619．解答：设三角形O C D 的面积为x ，梯形的高为h ，则：1()42A B C D h +=．因为5A B =，3C D =，所以1h =． 因为1322O C D O B C B C D S S S C D h ∆∆∆+==⨯=，所以32O B C O C D S S ∆∆=-，即32O B C S x ∆=- ……………………①同理可得512O A B O B C S S x ∆∆=-=+ ………………………②因为O AD O C D O BC O C D S S S S ∆∆∆∆+=+，所以O AD O BC S S ∆∆=． ……③ 由三角形面积公式得O AB O AD O BCO C DS S AO S O CS ∆∆∆∆==，即O AB O AD O BCO C DS S S S ∆∆∆∆=所以O AB O C D O BC O AD S S S S ∆∆∆∆⨯=⨯ ………………………………④ 由①，②，③，④得33(1)()()22x x x x +=--，所以916x =，即916O C D S ∆=．所以O C D ∆的面积为916．14．答案：l 59．解答：因为48能被3整除，所以“第十四届”所表示的数能被3整除，即“第十四届”的四个数字之和能被3整除．又因为1+2+3+…+9=45能被3整除，所以“华杯赛”表示的数的数字之和也能被3整除，即“华杯赛”所代表的数能被3整除．因为48能被4整除，而且“祝”字是4，“贺”字是8，所以“届”为偶数，只能取2或6．又“祝贺”与“华杯赛”的乘积为四位数，所以“华”字代表的数字只能是1．否则，即使“华杯赛”取最小的三位数为213，48×213=10224是五位数，所以取其它的三位数将更不符合要求．(1)当“届”取数字“2”时，则“赛”字只能是9，此时，算式是：⨯=481杯9第十四2．因为余下的4个数字3，5，6，7中，只有5与10的和能被3整除，所以“杯”字只能取5．此时，48×159=7632，符合要求．故“华杯赛”所代表的整数是159．(2)当“届”取数字“6”时，则“赛”取数字“2”或“7”．①若“赛”取数字“2”时，此时算式是⨯=481杯2第十四6．因为3与3，5，7，9的和分别为6，8，10，12，所以“杯”可以取数字“3”或“9”．但是48×132=6336，48×192=9216，显然不符合要求．②若“赛”取数字“7”时，此时算式是⨯=481杯7第十四6．因为8与2，3，5，9的和分别为10，11，13，17均不能被3整除，所以不存在“1杯7”使得等式⨯=481杯7第十四6成立．所以“华杯赛”所代表的整数为l59．。

第14届世界奥林匹克数学竞赛（中国区）选拔赛---------------------------------------------------------------------------------考生须知：1. 每位考生将获得考卷一份。

考试期间，不得使用计算工具或手机。

2. 本卷共120分，选择题每小题4分，填空题每小题5分，解答题共5小题，共50分。

3. 请将答案写在本卷上。

考试完毕时，考卷及草稿纸会被收回。

4. 若计算结果是分数，请化至最简。

八年级地方晋级赛初赛B 卷（本试卷满分120分 ，考试时间90分钟）一、选择题（每小题4分，共40分）1．已知x 没有平方根，且|x |=125，则x 的立方根为（ ）A ．15B ．－15C ．5D ．－5 2．若k ＜13＜k ＋1（k 是整数），则k 的值为（ ）A ．2B ．3C ．4D ．5 3．下列结论中，正确的是（ ）A ．若a ＞b ，则a 1＜b1B ．若a ＞b ，则a 2＞b 2C ． 若a ＞b ，则1－a ＜1－bD ． 若a ＞b ，则ac 2＞bc 24．如图，有一个△ABC ，现以B 点为圆心，AB 长为半径画弧，交BC 于D 点，以C 点为圆心，AC 长为半径画弧，交BC 于E 点.若∠B ＝40°，∠C ＝36°，则关于AD 、AE 、BE 、CD 的大小关系，下列正确的是（ ）A ．AD ＝AEB ．AD ＜AEC ．BE ＝CD D ．BE ＜CD第4题图 第6题图 第7题图 第8题图5．有一副美丽的图案，在其顶点处由四个正多边形镶嵌而成，其中三个分别为正三角形、正四边形、正六边形，则另一个为（ ）A ．正六边形B ．正五边形C ．正四边形D ．正三角形 6．如图，已知D ，E 分别是△ABC 的边BC 和边AC 的中点，连接DE ，AD ，若 S △ABC ＝24cm 2，则△DEC 的面积为（ ）A ．4cm 2B ．6cm 2C ．8cm 2D ．12cm 27．如图，在△ABC 中，点D 、E 、F 分别在边BC 、AB 、AC 上，且BD ＝BE ， CD ＝CF ，∠A ＝70°，那么∠FDE 等于（ ）A ．55°B ．45°C ．45°D ．35°8．如图，两个正六边形的边长均为1，其中一个正六边形的一边恰好在另一个正六边形的对角线上，则这个图形外轮廓线的周长是（ ）A ．8B ．9C ．10D ．129．已知，如图，∠AOB ＝30°，点M 1，M 2，M 3…在射线OB 上，点N 1，N 2，N 3…在射线OA 上，△M 1N 1M 2，△M 2N 2M 3，△M 3N 3M 4，…均为等边三角形．若OM 1＝1，则△M n N n M n +1的边长为（ ）A ．2nB ．2n +1C ．2n -1D ．2n10．在平面直角坐标系中，点A 的坐标为（1，1），点B 的坐标为（11，1），点 C 到直线AB 的距离为5，且△ABC 是直角三角形，则满足条件的C 点有（ ）A ．4个B ．5个C ．6个D ．8个第9题图 第15题图 第16题图 二、填空题（每小题5分，共30分）11．在实数0，－3，2，－2中，最小的是 ．12．在Rt △ABC 中，∠C =90°，AB ＋BC =12cm ，∠A =30°，则AB = cm ．13．已知a ，b 满足ab ＝1，那么112+a ＋112+b ＝ ．14．有两个正多边形，它们的边数之比是1:2，内角和之比为3:8，则这两个多边形的边数之和为 ．15．如图，在等边△ABC 中，AC =9，点O 在AC 上，且AO =3，点P 是AB 上一动点，连接OP ，将线段OP 绕点O 逆时针旋转60°得到线段OD .要使点D 恰好落在BC 上，则AP 的长是 ．16．如图，矩形ABCD 中，AB =2，AD =3，点E 、F 分别是AD 、DC 边上的点，且EF =2，点G 为EF 的中点，点P 为BC 上一动点，则P A ＋PG 的最小值为 ．三、解答题（共5小题，共50分）17．已知有理数x 、y 满足等式：2x ＋3y =10．（1）若x =21，求y 的值；（4分）（2）若x ≥21，求y 的取值范围．（4分）18．雨伞的中截面如图所示，伞骨AB =AC ，支撑杆OE =OF ，AE =31AB ，AF =31AC ，当O 沿AD 滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD 与∠CAD 有何关系？说明理由．（10分）19．如图，AD 是△ABC 的角平分线，DE 、DF 分别是△ABD 和△ACD 的高，求证：AD 垂直平分EF ．（10分）20．为支援非洲贫困地区，某慈善组织计划用“义捐义卖”活动中筹集的部分资金用于购买A 、B 两种型号的学习用品共1000件，已知A 型学习用品的单价为20元，B 型学习用品的单价为30元.（1）若购买这批学习用品用了26000元，则购买A 、B 两种学习用品各多少件？ （5分）（2）若购买这批学习用品的钱不超过28000元，则最多购买B 型学习用品多少件？（5分） 21．如图①，Rt △ABC ≌Rt △EDF ，∠ACB ＝∠F ＝90°，∠A ＝∠E ＝30°，AD =DB =DC ，△EDF 绕着边AB 的点D 旋转， DE ，DF 分别交线段．．AC 于点M ，K ． （1）观察：（i ）如图②、图③，当∠CDF ＝0°或60°时，AM ＋CK _______MK （填“＞”， “＜”或“＝”）；（2分） （ii ）如图④，当∠CDF ＝30° 时，AM ＋CK MK （填“＞”或“＜”）． （2分）（2）猜想：如图①，当0°＜∠CDF ＜60°时，AM ＋CK _______MK ，请证明你的 结论．（4分）（3）如果MK 2＋CK 2＝AM 2，请直接写出∠CDF 的度数．（注：在△ABC 中，如 果AB 2＋BC 2＝AC 2，则∠B ＝90°）（4分）图① 图② 图③ 图④。

级初赛A 卷答案一、选择题。

（每小题4分，共40分）1．B 2．A 3．Ａ 4．B 5．A6．C 7．C 8．B 9．B 10．D2．∵a =1，b =33≈0.577，c =55≈0.447，∴1＞0.577＞0.447，即a ＞b ＞c . 4．∵点A （m ，－3），B （3，2m －1），且直线AB ∥x 轴，∴2m －1=－3，解得m =－1.5．由题可知∠CDE =180°－∠DEC －∠C =180°－47°－55°=78°，又∠CDE = ∠B ＋∠F ,所以∠F =78°－43°=35°.6．∵x =2是不等式（x －5）（ax －3a ＋2）≤0的解，∴（2－5）（ax －3a ＋2）≤0，解得a ≤2，∵x =1不是这个不等式的解，∴（1－5）（a －3a ＋2）＞0，解得：a ＞1，∴1＜a ≤2.7．在长方形ABCD 中,∠B =90°，∵BP =2，AP =4，∴∠BAP =30°=∠CPQ .∵AP =PQ ，∠B =∠C =90°，∴△ABP ≌△PCQ ，∴AB =PC =BC －BP =AD －BP=2＋23－2=23.8．①以AB 为等腰三角形的腰.以点A 为圆心，AB 长度为半径作圆，这个圆与坐标轴有4个交点P 1、P 2、P 3、P 4；同样以点B 为圆心，AB 长度为半径作圆，这个圆与坐标轴有4个交点P 5、P 6、P 7、P 8.②以AB 为等腰三角形的底.只有当线段AB 的中点经过原点O 时，作AB 的中垂线.这条中垂线与坐标轴的交点只有O 点，此时A 、B 、O 三点共线，不能构成三角形.综上所述，作图如下，这样的P 点最少有8个.9．设S =1＋3＋32＋33＋…＋32014，则有3S =3＋32＋33＋34＋…＋32015，所以3S－S =32015－1，解得：S =21（32015－1），则1＋3＋32＋33＋…＋32014=21（32015－1）.10．连接EH 和FG ，四边中点E 、F 、G 、H 是入球孔，由此可知，四边形EFGH 是平行四边形，根据三角形等底同高原则，不论点O 在什么位置，阴影部分的面积正好是平行四边形EFGH 的一半，即S 阴影=21S 平行四边形EFGH =21×(21 S 长方形ABCD )=41S 长方形ABCD ，由图可知S 阴影＋S 空白=S 长方形ABCD ，所以S 阴影=31S 空白，所以阴影部分面积比空白部分面积少32.二、填空题。

11997第十四届全国初中数学联赛第一试一、选择题本题共有6个小题，每一个小题都给出了以A ．B ．C ．D 为代号的四个答案，其中只有一个答案是正确的．请将正确的答案用代号填在各小题的括号内．1．下述四个命题中，假命题的个数是（ ）⑴一个数的倒数等于自身，那么这个数是1；⑵对角线互相垂直且相等的四边形是正方形；⑶2a 的平方根是||a ±；⑷大于直角的角一定是钝角．A ．1个B ．2个C ．3个D ．4个23253x <+-，那么满足上述不等式的整数x 的个数是（ ）A ．4B ．5C ．6D ．73．若实数a ，b ，c 满足2229a b c ++=，代数式222()()()a b b c c a -+-+-的最大值是（ ）读万卷书 行万里路A ．27B ．18C ．15D ．124．给定平面上n 个点，已知1，2，4，8，16，32都是其中两点之间的距离，那么点数n 的最小可能值是（ ）A ．4B ．5C ．6D ．75．如图，在梯形ABCD 中，AD C =，30B ∠=︒，60C ∠=︒，E ，M ，F ，N 分别为AB ，BC ，CD ，DA 的中点，已知7BC =，3MN =，则EF 的值为（ ）A ．4B ．142C ．5D ．66．如图，已知A B ∠=∠，1AA ，1PP ，1BB 均垂直于11A B ，117AA =，116PP =，120BB =，1112A B =，则AP PB +等于（ ）A ．12B ．13C ．14D ．15二、填空题1．从等边三角形内一点向三边作垂线，已知这三条垂线的长分别为1，3，5，则这个等边三角形的面积是_________．2．当a 取遍0到5的所有实数值时，满足3(38)b a a =-的整数b 的个数是________．3．若a ，b 满足35||7a b =，则3||S a b ==的取值范围是_________．N GFED MBA B 1P 1A 1BPA34．若正整数x ，y 满足221997x y +=，则x y +等于__________．第二试一、设P 为等腰直角三角形ACB 斜边AB 上任意一点，PE 垂直AC 于点E ，PF 垂直BC 于点F ，PG 垂直EF 于点G ，延长GP 并在其延长线上取一点D ，使得PD PC =，试证：BC BD ⊥，且BC BD =．二、已知a ，b 为整数，且a b >，方程233()40x a b x ab +++=的两个根α，β满足关系式(1)(1)(1)(1)ααββαβ+++=++，试求所有的整数点对()a b ，．三、已知定理：“若三个大于3的质数a ，b ，c ，满足关系式25a b c +=，则a b c ++是整数k 的倍数”．试问：上述定理中的整数k 的最大可能值是多少？并证明你的结论．1997第十四届全国初中数学联赛解 答一九九七年第一试一、选择题1．CFG PE DCBA读万卷书 行万里路【解析】 ⑴ 1-的倒数也是他本身，所以这个命题不对．⑵ 对角线互要垂直且相等的平行四边形才是正方形，所以这个命题也不对．⑶ 2a 的平方根是a ±，这是对的．⑷ 大于直角的角一定是钝角，钝角是90-180度之间的角．故选择C ．2．C【解析】3253x <<+-()43241.732 1.41432=-+≈，1232<<+，()253 2.236 1.73253=+-，≈27853<<-．所以27x ≤≤，共有6个，选择C ．【点评】 本道题关键是通过根式的分母有理化求出上下限的大概的取值，由于所求得是整数，所以关键是确定上下限的整数部分，就能得出结论．53．A【解析】 ()()()()()22222222a b b c c a a b c ab bc ca -+-+-=++-++，考虑到等式()()22222a b c a b c ab bc ca ++=+++++，将两个等式相加得到()()()()()2222222327a b b c c a a b c a b c -+-+-+++=++=，当0a b c ++=时，()()()222a b b c c a -+-+-有最大值27．故选A ．【点评】 本题的关键是根据()2ab bc ca ++联想到公式()()22222a b c a b c ab bc ca ++=+++++，这要求我们对这些基本的公式非常熟悉，并且能够灵活运用．4．D【解析】 观察出这些距离都是2的n 次幂，而124+<，1248++<，…，1241632++++<L ，即这些线段中的任几条都不能构成一个多边形，这六条线段也不能构成六边形，所以至少要7个点才能满足条件，选择D ．【点评】 这是一道很特殊的题，有一道题是要求组成64以下各种质量所需要的砝码的最少个数，答案就是1，2，4，8，16，32，和这道题有的有一定的类似之处，在解题过程中我们要注意一些特殊数列的性质．5．A读万卷书 行万里路【解析】 延长BA CD ，交于点H ，∵3060B C ∠=︒∠=︒，，∴90BHC ∠=︒，在Rt GHC △中，M N H ，，三点共线，因此72HM =,12HN =， ∴12AN =． 故：()1142AD EF AD BC ==+=，．故选A ． 【点评】 首先由于题中出现3060︒︒，，很显然我们要做的辅助线就是延长梯形的两边，这样可以构造出一个直角，然后可以利用特殊三角形的各边之比求出结果．6．B【解析】 如图，延长BP 交1AA 于A '，过P 作PP '平行于11A B 交1AA 于P '，过A '作A D '平行于11A B 交1BB 于.D∵A B ∠=∠，∴AP A P '=，∴AP A P '''=，∵111761AP AA P A ''=-=-=，∴212AA '=⨯=，HA BD EFGN DP'A'A PBA 1P 1B 17∴()11201725BD BB A A '=-=--=．由勾股定理得：22221151213A B A B BD '++，即：13AP PB +=，故选B ．【点评】 本题很显然要利用勾股定理来做．二、填空题1．273【解析】 解法一：如图所示ABC △为正三角形，351OD OE OF ===，，．过O 点作GH 平行于AB ，连接OC ，显然GHC △也为正三角形，不妨设ABC △边长为a ，则ABC △23，ABC △3，则可以知道GHC △31-，由于三角形ABC △，GHC △3123a - 所以GHC △22231333213a ⎛⎫- ⎪⎫=-⎪⎪⎝⎭．同时，由于三角形ABC GHC ，△△相似，3123a -所以GHC △2323a a -GHC △的面积等于HOC GOC ，△△读万卷书 行万里路之和，故GHC △的面积为(23123523a a -+8331⎫=-⎪⎪⎝⎭， 28333311⎫⎫--⎪⎪⎪⎪⎝⎭⎝⎭， 可得：63a =所以三角形面积为：273解法二：还可以有另外的解法，ABC △的面积为AOC △，BOC AOB ，△△面积之和，即()()11135422AB FO BC DO AC EO a a ⨯+⨯+⨯=++=,故有：234a ，可得：63a =所以三角形面积为：273【点评】 对于这种求面积的题，我们首先考虑它的结论，由于最后求出来的是正三角形的在积，所以，解题过程中正三角形的边长肯定是能求出来的，所以我们可以假设正三角形的边长是a ；同时，对于求面积的题来说，通常的等式都是通过用不同的方法求出面积而建立的，尤其是对于四边形来说，更是应该转化成不同的三角形来做．2．13【解析】 未知数不确定，且有未知数是整数这个条件约束的时候，一般情况下是求出未知数的取值范围，确定未知数各种取值，再带入题中的已知条件检验．∵223416839b a a a ⎛⎫=-=-- ⎪⎝⎭，H OG F EDCBA9()()2005113f f ==，．所以，43a =时，b 有最小值169-，5a =时，b 有最大值2113．∴1610599b -≤≤． 即b 可以取值：10111-L ，，，，，共有13个．【点评】 求b 的值有多少种有时候也就是要求b 的取值范围，在求b 的取值范围的时候，通常有两种方法可行，一是将式子看成是关于a 的一元二次方程，通过判别式的取值可以求出b 的取值，二是通过配方法直接求出b 的取值范围，本题利用的是配方法．3．211453S -≤≤ 【解析】 分别看S a S 和5b 之间的关系：因为357a b +=，23a b S =，b 19215a S +，两式消去a 有：19143b S =-，a b 均大于0，因此：21501430S S +-，≥≥，则：211453S -≤≤． 【点评】 本题只需要注意基本的概念，一个数的绝对值，或一个正数的算术平方根大于等于0，然后解关于S 的不等式就能得出结果．读万卷书 行万里路4．63【解析】 1997为奇数，所以x y ，两个数一个是奇数，一个是偶数，不妨设x 为奇数，y 为偶数．同时，完全平方数的尾数只可能是145691997，，，，，的末尾数字为7，所以，x y ，的各位数字必是14，或16，或94，或96，．y 是偶数，所以x y ，除以4余0，而1997除以4余1，所以x 除以4余1．由于21997x <可知45x <，因此x 可能的值为19212941，，，，．经检验，仅当29x =时，有34y =时有：22229341997+=，293463+=．【点评】 对于这些不定方程的题，应该从多方面的情况来考虑：奇偶性，被3，5，8，9等数整除的余数，这些整数的偶数等，一个是要确定未知数的可能取值范围，然后就是根据这些讨论进一步的缩小未知数的取值范围，再带入方程检验．第二试一、【解析】 证明：显然只要证明PDB PCB △≌△，就能得出题中所要证明的两个结论．∵EPG EFP CPF ∠=∠=∠，∴45DPB APG EPG ∠=∠=︒+∠45CPF =︒+∠BPF CPF =∠+∠BPC =∠．ABCDE PG F读万卷书 行万里路11有∵PC PD PB =，公共，可以得到：PDB PCB △≌△，∴BC BD =．45PBD CPB ∠=∠=︒，故90CBD ∠=︒，∴BC DB ⊥．【点评】 首先应该根据题目所要证明的结论，分析所要证明的实质上是两三角形的全等，然后题中要证明的两三角形已经有两边相等，很显然我们要证明的只是两边所加的角相等即可，通过这样的分析很容易就能一推到底．二、【解析】 由韦达定理得到()43a b ab αβαβ⎧+=-+⎪⎨=⎪⎩， 代入到关系式()()()()1111ααββαβ+++=++中，得到()241a b ab +-=， 即()21a b -=，由于a b >，所以1a b -=，即1a b =+， 代入到原方程中得到()()23321410x b x b b ++++=．2121290b b =-+△≥，即()2214b +≤，所以b 只可能是0或1-，对应的a 是1或0． 【点评】 这是一道一元二次方程的整数根问题，这种题目在二试中经常出现，解这种题的关键在得出一个关于整系数之间的关系，对于本题来讲是利用韦达定理得出1a b -=，接下来通常可以利用判别式缩小范围得到最后的答案．读万卷书 行万里路12三、【解析】 由25a b c +=，知()2532a b c a b a b a b ++=+++=+，即a b c ++至少是3的倍数，我们设a b ，被3除的余数是m n ，．由于a b ，是大于3的质数，所以m n ，都不为零，若12m n ==，或者21m n ==，则25c a b =+是3的倍数，与c 是质数矛盾．所以只能1m n ==或者2m n ==，若1m n ==或者2m n ==则2a b +必然是3的倍数，此时()32a b c a b ++=+必是9的倍数，即k 可以为9． 现在我们来说明9是最大的，设4743a b c ===，，，则54a b c ++=，当5850a b c ===，，时63a b c ++=，而()54639=，，所以9是最大的．综上，9是最大可能的结果．【点评】 这是一道数论的题目，关键在于发现a b c ++是3的倍数，在对a b ，被3除的余数分情况讨论，可得出9满足题意．有些同学写到这里就完了，题中求的是最大的，所以必须说明9是最大的满足题意的数，这道题很容易说胆，举个简单的例子即可．。