基本偏差表

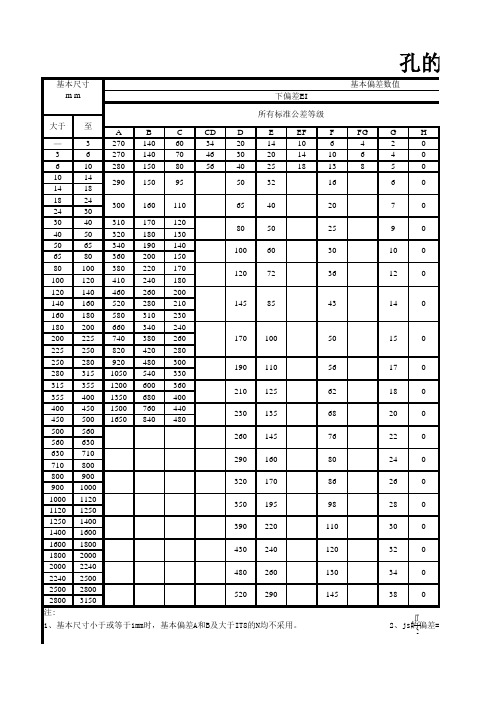
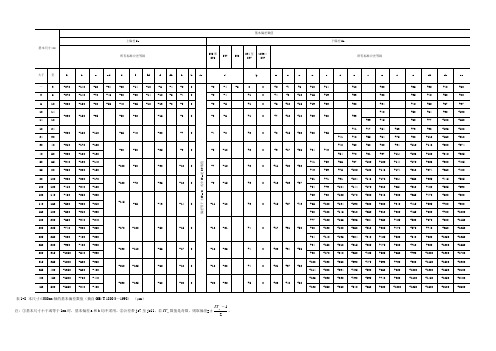
基本偏差表介绍在统计学中，基本偏差表是用来衡量估计量的不准确程度的一种工具。

它可以帮助我们了解样本估计值和总体真值之间的差距，并提供了一种评估统计模型的有效性的方法。

本文将深入探讨基本偏差表的概念、计算方法以及在实际应用中的作用。

什么是基本偏差表？基本偏差表是一种用来度量样本估计值与总体真值之间差距的工具。

在统计学中，我们常常需要通过样本数据来估计总体参数，如均值、方差等。

然而，由于样本的有限性，我们所得到的估计值往往与总体真值存在一定的差异，这就是偏差。

基本偏差表通过测量估计值和总体真值之间的平均差异来量化估计的不准确性。

它通常包含了一系列的假设条件，并给出了在不同偏差情况下的估计误差。

通过分析偏差表，我们可以获得关于估计值的更多信息，从而更好地评估统计模型的可靠性。

如何构建基本偏差表？构建基本偏差表的关键是确定偏差的类型和程度。

常见的偏差类型包括采样偏差、选择偏差、记忆偏差等。

在构建偏差表时，我们需要制定适当的修正方法来消除或减小这些偏差。

构建基本偏差表的步骤如下： 1. 定义总体参数：首先，我们需要明确要估计的总体参数，如总体均值、总体方差等。

2. 设定估计方法：选择适当的估计方法，如样本均值、样本方差等。

3. 构建假设条件：在偏差表中，我们需要假设一些条件，如总体分布的形状、样本的大小等。

这些假设条件将影响到偏差的大小和方向。

4. 计算估计偏差：根据假设条件，计算估计值与总体真值之间的偏差。

可以通过数学公式或模拟方法进行计算。

5. 绘制偏差表：将计算得到的偏差数据整理成表格或图形的形式，以便于后续分析和比较。

构建基本偏差表需要根据具体情况进行调整和细化，确保偏差的类型和程度充分考虑，以便得到准确的估计结果。

基本偏差表的应用基本偏差表在统计学中具有重要的应用价值。

它可以帮助研究人员评估估计的准确性，并检验假设条件的合理性。

以下是基本偏差表的一些常见应用：1. 实验设计在实验设计中，我们常常需要对实验对象进行观察和测量，并通过样本数据来推断总体的特征。