当前位置：文档之家 › 3-1立体表面上点的投影

3-1立体表面上点的投影

  • 格式：doc
  • 大小：114.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

3-1-立体表面上点投影解析

3-1-立体表面上点投影解析
b
步骤：1、过m’点作m’e’//a’b’；
s"
m
a"(c") b"
2、求出E在H面的投影e，作em//ab,得到点M在H面投影m；
3、根据“高平齐，宽相等”，由m’和m求出m”。
三、圆柱体表面上点的投影
例：已知圆柱面上M点和N点 的正面投影，求水平投影和侧面 投影。
分析：点在圆柱面上，利用水平
投影积聚性，可以求出点M和点 N的水平投影。
由于棱柱的表面都是平面，所以在棱柱的表面上取点 与在平面上取点的方法相同。
a′ b′
a”
b”
AB DC
d′ c′ a(d)
d”
c”
b(c)
平面的投影可见，点的投影可见； 平面积聚成直线，点的投影可见
如何判断可 见性？
例：已知六棱柱ABCD侧表面上点M的V面投影m’， 求该点的H面投影m和W面投影m″。
1.培养学生 正确分析和 解决问题的 能力； 2.培养学生 理论联系实 践、举一反 三的能力。
1.激发学生 良好的合作 意识； 2.培养学生 具有耐心细 致的工作作 风和严肃认 真的工作态 度。
1.让学生在 实践中找到 学习乐趣， 提高学习兴 趣； 2.培养学生 自学的能力。
重点难点
重点
1.根据已知点 的投影绘制其 余点的投影； 2.正确利用辅 助线或辅助圆 绘制立体表面 上点的投影。
n’ (n”)
(m’)
m”
不可 见
m n
M N
练习
已知下列各平面立体的两视图，补画第三视图，并 作出立体表面上点M、N的另外两个投影。
练习2
n’ (m’)
m”
n”
m n
小结

机械制图教案——第3章 立体的投影

机械制图教案——第3章 立体的投影

第3章立体的投影一、本章重点：1.平面立体和曲面立体投影的画法，及立体表面点的投影。

2.立体与平面相交其交线的画法，既求截交线。

3.两回转体轴线垂直相交其交线的画法。

4.立体的尺寸标注。

二、本章难点：1.圆球和圆环的投影及表面上点的投影。

2.圆锥、圆球被平面截切后，截交线的画法。

3.求作相贯线。

三、本章要求：通过本章的学习，要掌握基本体的三面投影画法，基本体表面点的投影，能够分析和绘制常见的截交线和两回转体轴线相交时的相贯线，掌握立体的尺寸标注的方法。

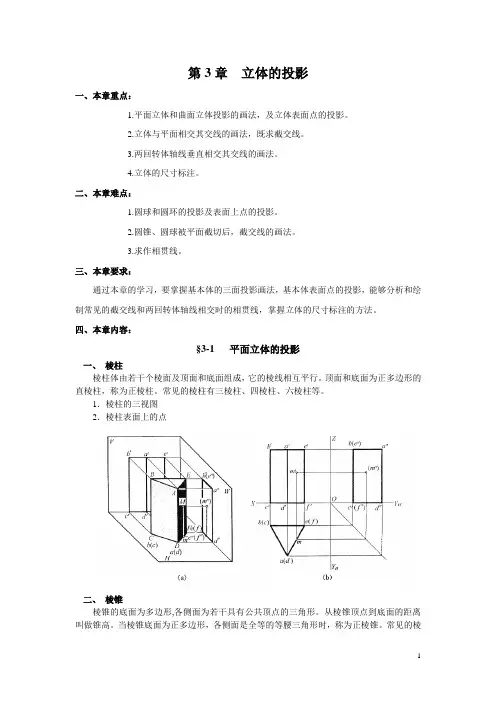
四、本章内容：§3-1 平面立体的投影一、棱柱棱柱体由若干个棱面及顶面和底面组成，它的棱线相互平行。

顶面和底面为正多边形的直棱柱，称为正棱柱。

常见的棱柱有三棱柱、四棱柱、六棱柱等。

1．棱柱的三视图2．棱柱表面上的点二、棱锥棱锥的底面为多边形,各侧面为若干具有公共顶点的三角形。

从棱锥顶点到底面的距离叫做锥高。

当棱锥底面为正多边形，各侧面是全等的等腰三角形时，称为正棱锥。

常见的棱锥有三棱锥、四棱锥、六棱锥。

1. 棱锥的三视图2．棱锥表面上的点§3-2曲面立体的投影曲面立体的表面是由一母线绕定轴旋转而成的，故称曲面立体，也称为回转体。

常见的回转体有圆柱、圆锥、圆球和圆环等。

一、圆柱1．圆柱面的形成圆柱面可看作一条直线AB围绕与它平行的轴线OO回转而成。

OO称为回转轴，直线AB称为母线，母线转至任一位置时称为素线。

这种由一条母线绕轴回转而形成的表面称为回转面，由回转面构成的立体称为回转体。

2．圆柱的三视图3．圆柱表面上的点二、圆锥1．圆锥面的形成圆锥面可看作由一条直母线围绕和它相交的轴线回转而成。

2．圆锥的三视图3．圆锥表面上的点三、圆球1．圆球面的形成圆球面可看作一圆（母线），围绕它的直径回转而成。

2．圆球的三视图3．圆球表面上的点四、圆环1．圆环的形成圆环面可看作由一圆母线，绕一与圆平面共面但不通过圆心的轴线回转而成。

图中的回转轴是铅垂线。

3-1-立体表面上点的投影

3-1-立体表面上点的投影

由于棱柱的表面都是平面，所以在棱柱的表面上取点 与在平面上取点的方法相同。
a′ b′
a”
b”
AB DC
d′ c′ a(d)
d”
c”
b(c)
平面的投影可见，点的投影可见； 平面积聚成直线，点的投影可见
如何判断可 见性？
例：已知六棱柱ABCD侧表面上点M的V面投影m’， 求该点的H面投影m和W面投影m″。
S
M
例：已知棱面SAB上点M的正面投影m‘，求作M点的 其余投影。
s'
Z
作图方法一
s'
s"
m
c' S
s"
a' b'
m
m
M
m
X
A
D
C a" O (c")
B
b"
a sc
m
b
a' d’ b' c' a"(c") b"
as
c
d
m
b
步骤：1、过M点作辅助线SD,连接s’m’,并延长交a’b’于d’,得到SD的V面投影 s’d’；
n'
投影积聚性，可以求出点M和点
N的水平投影。
步骤：
1、由于m’不可见所以在水平面
的投影在后半圆的圆周上等到m。 m
2、根据“高平齐，宽相等”， 由m’和m求出m”。
3、同理求出n和n’。
n
m" (n")
四、圆锥表面上点的投影
由于圆锥面的投影没有积聚性，所以必须在圆锥 上作一条包含该点的辅助线（直线或圆），先求出辅 助线的投影，再利用线上点的投影关系求出圆锥表面 上点的投影

立体表面上点的投影

立体表面上点的投影
图3－6用辅助线法在圆锥面上取点
边画图边讲解作图方法与步骤。
作法二：辅助圆法如图3－7<a）所示，过圆锥面上点M作一垂直于圆锥轴线的辅助圆，点M的各个投影必在此辅助圆的相应投影上。在图3－7<b）中过m′作水平线a′b′，此为辅助圆的正面投影积聚线。辅助圆的水平投影为一直径等于a′b′的圆，圆心为s，由m′向下引垂线与此圆相交，且根据点M的可见性，即可求出m。然后再由m′和m可求出m″。
教案重点
圆锥体和圆球体的三视图画法及表面取点、取线的作图方法
教案难点
在圆球体表面取点、取线的作图方法
教案内容、方法及过程
教案方法：用教案模型辅助讲解。
教案过程：
一、课前提问
1、棱柱、棱锥投影分析和投影特征以及表面求点的方法。
2、圆柱体的投影分析和投影特征以及表面求点的方法。。
二、引入新课题
上次课我们学习了平面立体和圆柱体的投影及表面求点，本次课我们继续学习其他几种曲面立体的投影及表面求点。
<a）<b）<c）<d）
<e）<f）<g）
图3－10平面立体的尺寸注法
2、曲面立体的尺寸标注
圆柱和圆锥应注出底圆直径和高度尺寸，圆锥台还应加注顶圆的直径。直径尺寸应在其数字前加注符号“φ”，一般注在非圆视图上。这种标注形式用一个视图就能确定其形状和大小，其他视图就可省略，如图3－11<a）、<b）、<c）所示。
作法一：辅助线法如图3－6 <a）所示，过锥顶S和M作一直线SA，与底面交于点A。点M的各个投影必在此SA的相应投影上。在图3－6<b）中过m′作s′a′，然后求出其水平投影sa。由于点M属于直线SA，根据点在直线上的从属性质可知m必在sa上，求出水平投影m，再根据m、m′可求出m″。

第三章 平面立体的投影及线面投影分析-第一讲

第三章 平面立体的投影及线面投影分析-第一讲

侧垂线（垂直于W面，同时平行于H、V面的直线）
Z
a
b Z
a(b)
V
a
b ab
A B O W
X
O b YH
YW
X
a
Ha
b
Y
侧面投影积聚为一点；水平投 影及正面投影平行于OX轴，且 反映实长。
投影面垂直线的投影特性
投影面垂直线的投影特性可概括如下： （1）直线在它所垂直的投影面上的投影积聚成一点； （2）该直线在其他两个投影面上的投影分别垂直于相应 的投影轴，且都等于该直线的实长。 事实上，在直线的三面投影中，若有两面投影平 行于同一投影轴，则另一投影必积聚为一点；只要空间 直线的三面投影中有一面投影积聚为一点，则该直线必 垂直于积聚投影所在的投影面。
直线倾斜于投影面 投影比空间线段短 ab=ABcosα
直线的分类
直线与投影面的夹角，称为直线与投影面的倾角。对水平投影面的倾 角叫水平倾角，用α表示；对正立投影面的倾角叫正面倾角，用β表示； 对侧立投影面的倾角叫侧面倾角，用γ表示。 投影面垂直线
特殊位置直线 直 线 一般位置直线
直线在投影图上表现出来的特性，常与直线对投影面的倾斜状态有 关。根据直线与投影面的倾斜状态，直线分为三种类型：投影面平行线、 投影面垂直线、任意倾斜直线。
根据从属性判断点与直线的相对位置
V
n'
m'
N A
a'
M X B
n' b'
m'
a'
b'
X
O
O
b
n
m
a
H
a m b n
注意：对于侧平线还需考察侧面投影。

3-1立体表面上点的投影

3-1立体表面上点的投影

02 新课表面上点的投影 三、圆柱体表面上点的投影 四、圆锥表面上点的投影 五、球面上点的投影
03 巩固提高
作出俯视图，并求表面点A、点B的投影。
a" (b")
03 巩固提高
作出左视图，并求表面点C的投影。
03 巩固提高
作出左视图，并求表面点A、点B的投影。
第三章 立体表面交线的投影作图
§3－1 立体表面上点的投影
01 预习检测
圆柱、圆锥的投影特性：
特性 分类
几何特点
投影特性
圆柱 上下底面为直径相等的两圆面，侧面为曲 面（回转面）。
回
转 体 圆锥 底面为圆面，侧面为回转面。
、一面视图为圆； 2、另两面视图是矩形线框。
、一面视图为圆； 2、另两面视图是等腰三角形线框。
B A
03 巩固提高
求作左视图及形体表面点投影。
P
B
04 评价总结
一、棱柱表面上点的投影 二、棱锥表面上点的投影 三、圆柱体表面上点的投影 四、圆锥表面上点的投影 五、球面上点的投影
05 任务布置
补画第三视图，并求表面点的投影。

项目三 基本体的投影


作图： （1) 先画出四棱锥的第三面投影图（图3-8(b))； （2) 因P面为正垂面，四棱锥的四条棱线与P面交点的V面投影1′、2′、 3′、4′可直接求出； （3) 根据直线上点的投影性质，在四棱锥各棱线的H、W面投影上，求出 相应点的投影1、2、3、4和1″ 、2″ 、3″ 、4″ ； （4）将各点的同面投影依次连接起来，即得到截交线的投影,它们是两 类似的四边形1234和1″ 2″ 3″ 4″ 。在图上去掉被截平面切去的部 分，即完成截头四棱锥的三面投影图。
• 4、圆锥 （1）圆锥的投影 圆锥面是由一条直母线SA，绕与它相交的轴线OO1旋转形成的，如 图3-5(a)所示。圆锥体表面是由圆锥面和底面组成。在圆锥面上任意位 置的素线，均交于锥顶点。 画法： 1) 画回转轴线的三面投影； 2) 画底圆的水平投影、正面投影和侧面投影。 3) 画正面投影中前后两半转向线的投影，侧面投影中左右两半转向 轮廓线的投影。
下面举例说明求平面立体截交线的方法和步骤。 例3-2：试求正垂面P与四棱锥的截交线，并画出四棱锥切割后的三面投 影图,如图3-8所示。 分析：由图3-8(a)可知，因截平面P与四棱锥的四个侧面都相交，所以截 交线为四边形。四边形的四个顶点为四棱锥四条棱线与截平面P的交点。 由于截平面P是正垂面，截交线的V面投影积聚为一斜线（用Pv表示）， 由V面投影可求出其H面投影与W面投影。
• 3、圆柱 （1）圆柱的投影 圆柱是由圆柱面和顶圆平面、底圆平面围成的。如图3-3所示，圆柱 面可以看作是一条直母线AE绕与它平行的的轴线oo1旋转而成。
在圆柱的V面投影中，前、后两半圆柱面的投影重合为一矩形，矩形 的两条竖线分别是圆柱的最左、最右素线的投影，也是前、后两半圆柱 面分界的转向线的投影。在圆柱的W面投影中，左、右两半圆柱面的投影 重合为一矩形，矩形的两条竖线分别是圆柱的最前、最后素线的投影， 也是左、右两半圆柱面分界的转向线的投影。矩形的上 、下两条水平线 则分别是圆柱顶面和底面的积聚性投影，如图3-3(c)所示。 在图3-3(d)中，圆柱面上有两点M和N，已知V投影n′和m′，且为可 见，求另外两投影。由于点N在圆柱的转向线上,其另外两投影可直接求 出；而点M可利用圆柱面有积聚性的投影，先求出点M的H面投影m，再由m 和m′求出m"。点M在圆柱面的右半部分，故其W面投影m"为不可见。 （2)圆柱表面上取线 例3-1：已知圆柱表面的曲线AE的V面投影直线a′e′，求其另外两 投影（图3-4）。

第3-1章棱柱及其表面点的投影

提问突出介绍波浪线和双线展示挂图信息反馈
教学环节
教学内容
教师活动
学生活动
时间
教学内容
边画图边讲解作图方法与步骤。
总结正棱柱的投影特征：当棱柱的底面平行某一个投影面时，则棱柱在该投影面上投影的外轮廓为与其底面全等的正多边形，而另外两个投影则由若干个相邻的矩形线框所组成。
（2）棱柱表面上点的投影
方法：利用点所在的面的积聚性法。（因为正棱柱的各个面均为特殊位置面，均具有积聚性。）
制造业通用能力目标
培养学生的读图能力
学习重点
1、棱柱的种类及其三视图画法。
2、在棱柱表面取点的作图方法
学习难点
立体表面求点
教法学法
教法：
1.讲授法、任务引领法（用教学模型辅助讲解）
2.讲授与课堂演示、举例相结合
学法：
听授法、课堂练习法
教学媒体
1.口头表达
2.板书
教学学习准备
教师：
1.基本体模型：三棱柱、四棱柱、五棱柱、六棱柱等
2.尺寸注法、小尺寸、简化法的挂图
学生：
教材、练习册、绘图工具
自制的三投影面体系模型、简单几何体模型
@@@@@学院理论课教案首页
教学环节
教学内容
教师活动
学生活动
时间
一、复习旧课
二、引入新课题
三、教学内容
一、复习旧课
结合作业复习直线和平面投影变换的作图方法和步骤。
二、引入新课题
机器上的零件，不论形状多么复杂，都可以看作是由基本几何体按照不同的方式组合而成的。
平面立体表面上取点实际就是在平面上取点。首先应确定点位于立体的哪个平面上，并分析该平面的投影特性，然后再根据点的投影规律求得。

3章点的投影

学习要求§3.1 点的投影§3.2 两点的相对位置第三章点的投影本章目录第3章点的投影点是构成形体的最基本元素，熟练掌握点的投影规律及其它们之间的相互关系，为学习直线、平面、曲线、曲面及立体等打下良好的基础。

本章将讨论本章学习基本要求熟练熟悉两点的相对位置的判别。

能熟练判别重影点的可见性。

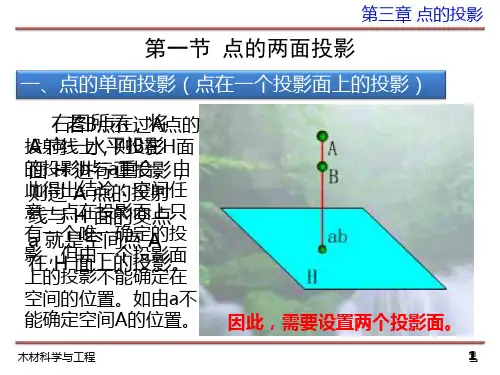
3.1.1 点在三面投影体系中的投影如图3－1(a)所示，将空间点Ａ放置在三面投影体系中，通过点Ａ分别向Ｈ面、Ｖ面和Ｗ面作垂直投射线，则三条投射线与三个投影面的交点分别为点Ａ在Ｈ面的投影a；在Ｖ面的投影a‘及在Ｗ面的投影a″。

a、a′、a″即为空间点Ａ的三面投影。

展开投影面体系后，如图３－１（b）所示。

动画演示点在三投影面中的表示:空间点用英文大写字母（如A、Ｂ…）表示，其投影用小写字母(如Ｈ面用a、b…)表示,V面投影用相应小写字母并在右上方加一撇(如a′、b′…）表示，W 面投影用相应小写字母并在右上方加两撇（如a″、b″…3.1.2 点的投影特征点在三面投影体系中的投影特征为：１．点的投影连线垂直于相应投影轴，如aa′⊥ox 。

a′a″⊥oz2．点的投影到投影轴的距离等于空间点到相邻投影面的距离。

a′a x = a″a y w=Aaaa x =a″a z =Aa′aa yH =a′a z =Aa″。

由上可知，点到某一投影面的距离等于点在另两投影面上的投影到相应投影轴的距离。

动画演示例3-1 已知点A 的水平投影a 及正面投影a′，求作点A 的侧面投影a″(图3-2a)。

分析：根据点在三面投影体系中投影特征：a′a″⊥oz ；aa x = a″az ，即可求得a″。

作图：(1)过a′作oz 轴的垂线；(2)量取aa x =a″a z ，a″即为所求，如图3-2（b ）所示。

用图3-2（c ）、（d ）、（e ）所示的三种方法也可求得同一结果。

动画演示3.1.3 特殊位置的点当点距某一投影面的距离为零时，该点便在此投影面内。

3-1 立体表面上点的投影解析


a'
a" 1"
1' A 1
1、过a’s’作圆锥表面上的素线，延长交底圆为1’。 步 骤： 2、求出素线的水平投影s1,得到H面投影a 。 3、求出素线的侧面投影s”1”,得到V面投影a”。
a s
方法二：辅助圆法
过M点作一平 行与底面的水平辅 助纬圆（垂直于轴 线的圆），则点M 各投影必在该圆的
a’
3、根据“高平齐，宽相 等”，由a’和m求出a”。
a
o
A
辅助纬圆
例：已知球面上点A的正面投影，求水平投影 和侧面投影。 方法二： 用辅助正平圆作图
a'
a"
A
辅助纬圆
a
练习
已知下列各平面立体的两视图，补画第三视图， 并作出立体表面上点M、N的另外两个投影。
练习1
n’
(m’) m”
(n”)
不可 见
m n M N
a′ d′
A D B
b′
a”
b” c”
c′
d”
C
a (d ) b (c )
如何判断可 见性？
平面的投影可见，点的投影可见； 平面积聚成直线，点的投影可见
例：已知六棱柱ABCD侧表面上点M的V面投影m’，求 该点的H面投影m和W面投影m″。
a′
m
b′
m
c′
d′
m’ m”
A M D
B C
a (d )
2、求出SD在H面的投影sd，m必在sd上，得到H面投影m； 3、根据“高平齐，宽相等”，由m’和m求出m”。
例：已知棱面SAB上点M的正面投影m’，求作M点的 其余投影。
s'
m
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（b）立体图（c）投影图
图3－8圆球的投影
边画图边讲解作图方法与步骤。
（2）圆球面上点的投影
方法：1）辅助圆法。圆球面的投影没有积聚性，求作其表面上点的投影需采用辅助圆法，即过该点在球面上作一个平行于任一投影面的辅助圆。
举例：如图3－9(a)所示，已知球面上点M的水平投影，求作其余两个投影。过点M作一平行于正面的辅助圆，它的水平投影为过m的直线ab，正面投影为直径等于ab长度的圆。自m向上引垂线，在正面投影上与辅助圆相交于两点。又由于m可见，故点M必在上半个圆周上，据此可确定位置偏上的点即为m′，再由m、m′可求出m″。如图3－9（b）所示
教案
授课题目
3-1立体表面上点的投影
教研室主任
教务科长
授课时数
2
教学方法
讲授
教具
黑板
授课班级
与时间
12级机电47
教学目标
知识目标：1、讲解圆锥体和圆球体的三视图画法及表面取点、取线的作图方法
2、讲解基本体的尺寸标注
技能目标：1、能够熟练运用辅助面法在平面立体和圆柱体表面取点、取线
2、能够正确标注基本体所需的尺寸
注：请根据内容多少自行添加页数
（a）（b）
图3－9圆球面上点的投影
边画图边讲解作图方法与步骤。
（二）基本体的尺寸标注
1、平面立体的尺寸标注
平面立体一般标注长、宽、高三个方向的尺寸，如图3－10所示。其中正方形的尺寸可采用如图3－10（f）所示的形式注出，即在边长尺寸数字前加注“□”符号。图3－10（d）、（g）中加“（）”的尺寸称为参考尺寸。
作法一：辅助线法如图3－6（a）所示，过锥顶S和M作一直线SA，与底面交于点A。点M的各个投影必在此SA的相应投影上。在图3－6（b）中过m′作s′a′，然后求出其水平投影sa。由于点M属于直线SA，根据点在直线上的从属性质可知m必在sa上，求出水平投影m，再根据m、m′可求出m″。
（a）立体图（b）投影图
教学重点
圆锥体和圆球体的三视图画法及表面取点、取线的作图方法
教学难点
在圆球体表面取点、取线的作图方法
教学内容、方法及过程
教学方法：用教学模型辅助讲解。
教学过程：
一、课前提问
1、棱柱、棱锥投影分析和投影特征以及表面求点的方法。
2、圆柱体的投影分析和投影特征以及表面求点的方法。。
二、引入新课题
上次课我们学习了平面立体和圆柱体的投影及表面求点，本次课我们继续学习其他几种曲面立体的投影及表面求点。
（b）立体图（c）投影图
图3－5圆锥的投影
边画图边讲解作图方法与步骤。
的投影特征：当圆锥的轴线垂直某一个投影面时，则圆锥在该投影面上投影为与其底面全等的圆形，另外两个投影为全等的等腰三角形。
（2）圆锥面上点的投影
方法：1）辅助线法。
2）辅助圆法。
总结圆锥
举例：如图3－6、3－7所示，已知圆锥表面上M的正面投影m′，求作点M的其余两个投影。因为m′可ቤተ መጻሕፍቲ ባይዱ，所以M必在前半个圆锥面的左边，故可判定点M的另两面投影均为可见。作图方法有两种：
图3－6用辅助线法在圆锥面上取点
边画图边讲解作图方法与步骤。
作法二：辅助圆法如图3－7（a）所示，过圆锥面上点M作一垂直于圆锥轴线的辅助圆，点M的各个投影必在此辅助圆的相应投影上。在图3－7（b）中过m′作水平线a′b′，此为辅助圆的正面投影积聚线。辅助圆的水平投影为一直径等于a′b′的圆，圆心为s，由m′向下引垂线与此圆相交，且根据点M的可见性，即可求出m。然后再由m′和m可求出m″。
（a）立体图（b）投影图
图3－7用辅助线法在圆锥面上取点
边画图边讲解作图方法与步骤。
2、圆球
圆球的表面是球面，如图3－8(a)所示，圆球面可看作是一条圆母线绕通过其圆心的轴线回转而成。
（1）圆球的投影
如图3－8（b）所示为圆球的立体图、如图3－8（c）所示为圆球的投影。圆球在三个投影面上的投影都是直径相等的圆，但这三个圆分别表示三个不同方向的圆球面轮廓素线的投影。正面投影的圆是平行于V面的圆素线A（它是前面可见半球与后面不可见半球的分界线）的投影。与此类似，侧面投影的圆是平行于W面的圆素线C的投影；水平投影的圆是平行于H面的圆素线B的投影。这三条圆素线的其他两面投影，都与相应圆的中心线重合，不应画出。
三、教学内容
（一）曲面立体的投影及表面取点
1、圆锥
圆锥表面由圆锥面和底面所围成。如图3－5（a）所示，圆锥面可看作是一条直母线SA围绕与它平行的轴线SO回转而成。在圆锥面上通过锥顶的任一直线称为圆锥面的素线。
（1）圆锥的投影
画圆锥面的投影时，也常使它的轴线垂直于某一投影面。
举例：如图3－5（b）所示圆锥的轴线是铅垂线，底面是水平面，图3－5（c）是它的投影图。圆锥的水平投影为一个圆，反映底面的实形，同时也表示圆锥面的投影。圆锥的正面、侧面投影均为等腰三角形，其底边均为圆锥底面的积聚投影。正面投影中三角形的两腰s′a′、s′c′分别表示圆锥面最左、最右轮廓素线SA、SC的投影，他们是圆锥面正面投影可见与不可见的分界线。SA、SC的水平投影sa、sc和横向中心线重合，侧面投影s″a″（c″）与轴线重合。同理可对侧面投影中三角形的两腰进行类似的分析。
（a）（b）（c）（d）
（e）（f）（g）
图3－10平面立体的尺寸注法
2、曲面立体的尺寸标注
圆柱和圆锥应注出底圆直径和高度尺寸，圆锥台还应加注顶圆的直径。直径尺寸应在其数字前加注符号“φ”，一般注在非圆视图上。这种标注形式用一个视图就能确定其形状和大小，其他视图就可省略，如图3－11（a）、（b）、（c）所示。
标注圆球的直径和半径时，应分别在“φ、R”前加注符号“S”，如图3－11（d）、（e）所示。
（a）（b）（c）（d）（e）
图3—11曲面立体的尺寸注法
四、小结
1、圆锥体、圆柱体的投影分析和投影特征以及表面求点的方法。
2、各种基本几何体应标注的尺寸数目和种类。
五、布置作业
习题集3－1（4）、（5）、（6）、（7）、（8）