闭合导线计算表
- 格式:xls
- 大小:18.50 KB
- 文档页数:1


一.坐标计算以下为基本计算公式:直线上计算公式:已知该条直线的方位角à,已知直线的起点或终点的坐标,顺线路方向时,计算点的里程知道,直线的起点或终点的里程知道,可推算出计算点与直线的起点的直线距离d,(即计算点的里程减去起点的里程,逆线路方向时,为直线终点的里程减去计算点的里程),计算坐标增量:∆x=d×cosà∆y=d×cosà计算点的坐标为,直线的起点或终点坐标加上坐标增量,式中方位角à从直线起点算时,为已知即给定的方位角,而从终点算时,à为该段直线的起始方位角加上180度。
à+180à起点计算点终点第一种曲线为两段直线中加一圆曲线,指仅存在圆曲线,如下第1点。
1.圆曲线上计算点相对于ZY或YZ 点的弦长和偏角D=2 RSinδδ=90×L/(πR)δ---------圆曲线偏角D ---------弦长L --------为弧长α=α(zy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。
α=α(yz)-δα------------为计算点的方位角,此α为逆着线路方向计算时。
α(zy)、α(yz)---------为圆曲线的起始方位角。
一般为已知。
计算点相对与直圆点或圆直点的坐标增量:△x=D*COSα△y=D*SINα坐标增量计算完毕后,要算某一点的坐标,用直圆点或圆直点的坐标加上计算点与直圆点或圆直点的坐标增量,即为计算点的坐标。
缓和曲线同理。
第二种曲线为两段直线中始端加一缓和曲线,末端加一缓和曲线,两段缓和曲线中加一圆曲线,如下第2点。
2.缓和曲线上计算点相对于HY或YH点的弦长和偏角δ=L²/6RL0X1=L-(L^5/40R²L0²)Y1=L³/6RL0D=√(X1²+Y1²)α=α(hy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。

1.做一个手表。
打开excel并制作表格,如图所示。
2.添加已知数据。
在表中添加点号和已知点坐标。
3.添加观察数据。
将此观测数据添加到表格中-距离和角度。
注意:添加角度时,请确保在度,分钟和秒之间使用空格。
4.将观察角“度秒”转换为“度”数。
在表格中输入:= int(左(b6,3))+ int(中(b6,4,3))/ 60 + int(右(b6,2))/ 3600可以获得转换值。
5.将鼠标移到空格的右下角,直到出现一个实心的十字。
按下鼠标并下拉。
完成所有观察角的转换。
6.计算起始方位角。
根据两个已知点计算两个点的方位角。
公式如下:=等级((PI ()*(1-符号(m6-m4)/ 2)-atan((l6-l4)/(m6-m4)))。
7.计算观测侧的方位角。
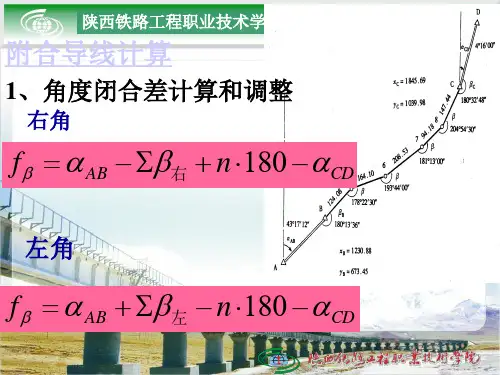
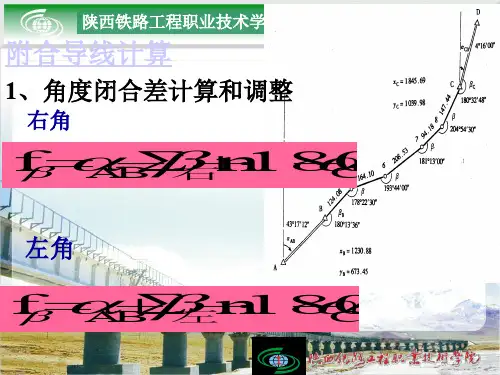
根据观测左角的方位角计算公式:起始方位角-180度+观测左角。
如图所示。
应该注意的是,结果为负且大于360度,因此如果使用函数进行判断。
公式:=如果((e5-180 + C6)<0,e5-180 + C6 + 360,如果((e5-180 + C6)> = 360,e5-180 + c6-360,e5-180 + C6))。
下拉-所有方位角均可用。
8.在计算结束时就知道了方位角。
参考步骤6,可以获得两个已知点的设计方位角。
9.计算闭合方位角的闭合误差。
闭合误差=导体设计方位角末端两个已知点的测量方位角。
如图所示。
检查关闭错误是否符合规格要求。
10.方位角闭合误差的分布。
误差分布原理:由于测量精度相等,因此误差是反符号,它均匀分布在每个观察角上。
用全站仪测量闭合导线的步骤:1.测量每个角度和距离。
2.通过内部计算来计算闭合误差,然后,如果满足公差,则根据内角数分配反符号。
3.计算校正后的方位角。
4.坐标增量计算。
5.获取每个点的坐标。
观测日期工位号A1→B1→C1→D1
成 像
清晰
阴
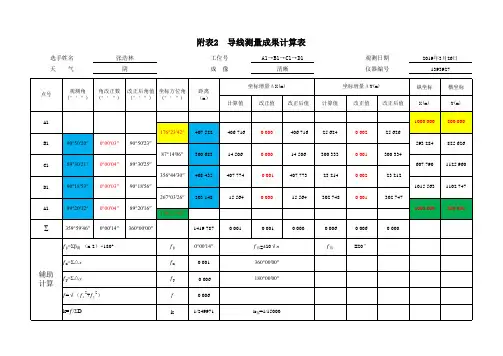
附表2 导线测量成果计算表
2019年3月26日仪器编号
1393927选手姓名天 气
张浩林
说明:本表中n表示闭合环的边数,本表四边形为例,即理论内角和为360°,本表中蓝色底纹部分为链接附件1观测手簿中平均结果数据,黄色底纹为已知数据,绿色底纹为校核数据,红色字体为手动输入数据。
角度改正数分配原则:正常为按边长的比例分配,特殊情况为长边少分,短边多分;坐标增量改正数分配原则:正常为按边长的比例分配,特殊情况为长边多分,短边少分。
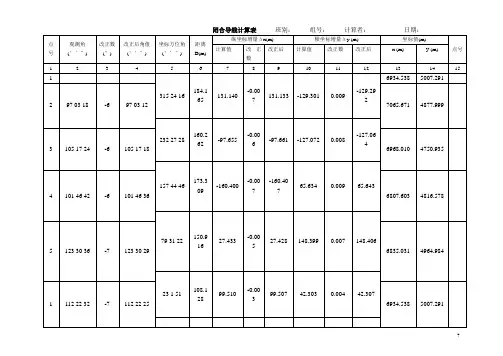
7 闭合导线计算表 班别: 组号: 计算者: 日期: 点号 观测角 (°′″) 改正数 (″) 改正后角值 (°′″) 坐标方位角(°′″) 距离D(m)
纵坐标增量Δx(m) 横坐标增量Δy (m) 坐标值(m)
点号 计算值 改正数 改正后 计算值 改正数 改正后 x (m)
y (m)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 315 24 16 184.165 131.140 -0.007 131.133 -129.301 0.009 -129.292 6934.538 5007.291
2 97 03 18 -6 97 03 12 7065.671 4877.999
232 27 28 160.262 -97.655 -0.006 -97.661 -127.072 0.008 -127.064 3 105 17 24 -6 105 17 18 6968.010 4750.935
157 44 46 173.309 -160.400 -0.007 -160.407 65.634 0.009 65.643 4 101 46 42 -6 101 46 36 6807.603 4816.578
79 31 22 150.916 27.433 -0.005 27.428 148.399 0.007 148.406 5 123 30 36 -7 123 30 29 6835.031 4964.984
23 1 51 108.128 99.510 -0.003 99.507 42.303 0.004 42.307 1 112 22 32 -7 112 22 25 6934.538 5007.291 8
2 ∑ 540 0 32 540 0 0 776.78 0.028 0 -0.037 0 闭合差和精度 fβ测= 32 f=0.0293
fβ允= 89 K=f /∑D=0.0293/776.78=1/33333