控制系统仿真及MATLAB语言--第四章 连续系统的离散化方法
- 格式:ppt
- 大小:663.00 KB
- 文档页数:44
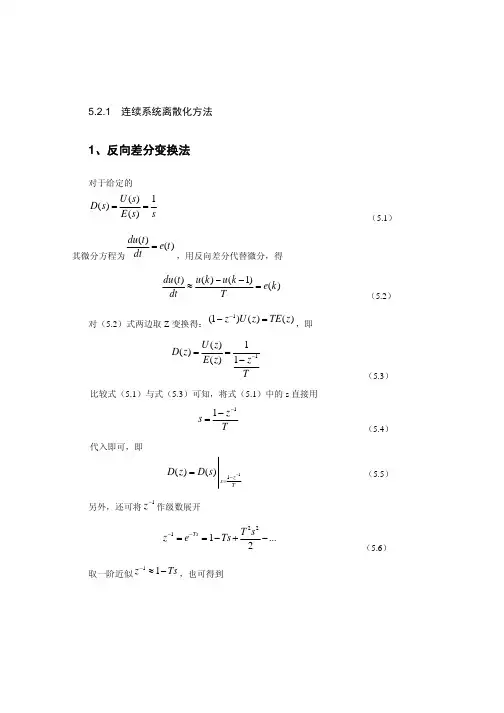



1实验一 离散系统的分析一 实验目的1.学习利用采样控制理论;2.使用MATLAB 理论进行分析;3. 学习利用z 变换与反变换分析离散控制系统;二、实验步骤1.开机执行程序C :\matlab \bin \matlab.exe (或用鼠标双击图标)进人MATLAB 命令窗口;2.运用所学自动控制理论z 变换与反变换,使用MATLAB 的基本知识分析离散控制系统的基本性质及进行控制系统的设计。
3. MATLAB 离散系统基本命令模型转换1)连续系统离散化sysd=c2d(sys,T) T 为采样时间sysd=c2d(sys,T,method)method 有四种模式:a. ‘zoh’---采用零阶保持器,b. ‘foh’---采用一阶保持器,c. ‘tustin’---采用双线性逼近(tustin )方法,d. ‘preqarp’---采用改进的(tustin )方法,2)离散系统连续化sys=d2c(sysd,T,method) T 为采样时间例 设)1(1)(+=s s s g , T=0.1s , 求G(z) 键入命令:sys=tf([1],[1 1 0]);c2d(sys,0.1) %采样时间0.1s得到离散传递函数:当采样时间取T=1s 时:0.004837 z + 0.004679 G (z )= ---------------------------- z^2 - 1.905 z + 0.9048 0.3679 z + 0.2642 G (z )= ---------------------------- z^2 - 1.368 z + 0.36792例 系统脉冲传递函数为6322.02644.03678.0)()(2+−+=z z z z R z C ,求离散单位阶跃响应。
解. 在MATLAB 窗口键入以下程序num=[0.3678 0.2644];den=[1 -1 0.6322];dstep(num,den)结果件下图:三、实验内容有系统1)其中K =10,T =0.25s,求单位阶跃函数r(t)=1 (t)作用下的响应。


连续函数离散化matlab程序连续函数离散化是在数值分析和科学计算中常常用到的一种技术。
离散化的目的是为了将连续函数转化为离散点的数据,以便在计算机程序中进行计算和处理。
在 MATLAB 中,我们可以使用一些内置函数来实现连续函数的离散化。
1. 离散化的概念离散化是将连续函数转化成离散点的数据。
我们可以将其想象成将一条曲线在数轴上映射成若干个点,每个点代表函数在该点处的函数值。
在实际的计算中,离散化不仅可以提高计算效率,还可以让我们将连续函数以表格的形式展示出来,使得我们更容易进行分析和处理。
2. 样条插值样条插值是一种常用的连续函数离散化方法,在 MATLAB 中可以使用spline 函数实现。
该函数可以根据一组已知的数据点(也就是离散的点),生成一个插值函数。
之后,我们就可以使用该插值函数来计算任意点处的函数值,并对其进行分析和处理。
3. 离散变量的生成离散化的第一步是生成函数在某一区间内的离散变量。
MATLAB 中的linspace 函数可以帮助我们生成等间距的离散点。
例如,下面的代码可以生成一个包含 100 个离散点的行向量 x:```matlabx = linspace(0, 1, 100);```这个代码使用了 linspace 函数,第一个参数是区间的起点,第二个参数是区间的终点,第三个参数是离散点的个数。
在这个例子中,代码生成了一个从 0 到 1 的区间,并且将该区间等分成了 100 个离散点。
4. 进行样条插值一旦我们生成了离散变量,我们就可以使用 MATLAB 中的 spline 函数来进行样条插值。
下面的代码演示了如何生成一个样条插值函数:```matlaby = sin(2 * pi * x);pp = spline(x, y);```这段代码中,我们使用了 spline 函数,它的第一个参数是离散点的横坐标 x,第二个参数是离散点的纵坐标 y。
函数返回一个插值函数pp,我们可以使用该插值函数对任意点进行估算。




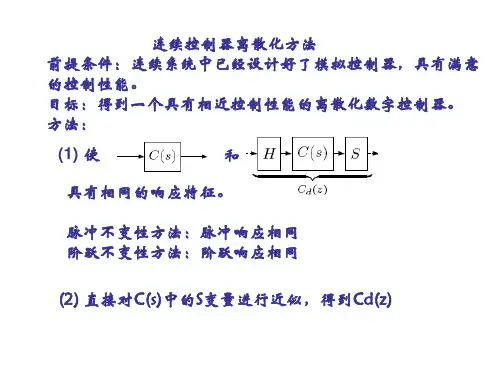
连续系统离散化处理基连续系统离散化处理的基本方法在数字汁算机上对连续系统进行仿真时,首先遇到的问题是如何解决数字计算 机在数值及时间上的离散性与被仿真系统数值及时间上的连续性这一基本问题。
从根本意义上讲,数字汁算机所进行的数值计算仅仅是“数字”计算,它表示 数值的精度受限于字长,这将引入舍入误差;另一方面,这种计算是按指令一步一 步进行的,因而,还必须将时间离散化,这样就只能得到离散时间点上系统性能。
用数字仿真的方法对微分方程的数值积分是通过某种数值计算方法来实现的。
任何 一种计算方法都只能是原积分的一种近似。
因此,连续系统仿真,从本质上是对原 连续系统从时间、数值两个方面对原系统进行离散化,并选择合适的数值计算方法 来近似积分运算,山此得到的离散模型来近似原连续模型。
如何保证离散模型的计 算结果从原理上确能代表原系统的行为,这是连续系统数字仿真首先必须解决的问 题。
设系统模型为:其中U ⑴为输入变量,y ⑴为系统变量;令仿真时间 间隔为/),离散化后的输入变量为!:仇),系统变量为y 仇),其中f 女表示仁妙。
如 果力(fj yO*川即5(4)"(儿)-"仇)©0,5(4)=沪仇)-y (S )"(对所有k=o,i,2,...),则可认为两模型等价,这称为相似 原理(参见图)。
实际上,要完全保证S (4)= 0,G .(4)= 0是很困难的。
进一步分析离散化引的误差, 随着计算机技术的发展,山i 甲規桃孚长引入的舍入误差可以忽略,关键是数值积分 算法,也称为仿真建模方法。
相似原理用于仿真时,对仿真建模方法有三个基本要 求:(1) 稳定性:若原连续系统是稳定的,则离散化后得到的仿真模型也应是稳定 的。
关于稳定性的详细讨论将在节中进行。
(2) 准确性:有不同的准确性评价准则,最基本的准则是:绝对误差准则:杠(.)=其中规定精度的误差量。
相对误差准则:‘以) y(F^)-y(S) y(S) <d(3)快速性:如前所述,数字仿真是一步一步推进的,即由某一初始值y (f 。