大学课程《物理化学》第一章(热力学第一定律)知识点汇总
- 格式:ppt
- 大小:5.23 MB
- 文档页数:6

热力学第一定律一、基本概念1.系统与环境敞开系统:与环境既有能量交换又有物质交换的系统。
封闭系统:与环境只有能量交换而无物质交换的系统。
(经典热力学主要研究的系统)孤立系统:不能以任何方式与环境发生相互作用的系统。
2.状态函数:用于宏观描述热力学系统的宏观参量,例如物质的量n、温度T、压强p、体积V等。
根据状态函数的特点,我们把状态函数分成:广度性质和强度性质两大类。
广度性质:广度性质的值与系统中所含物质的量成正比,如体积、质量、熵、热容等,这种性质的函数具有加和性,是数学函数中的一次函数,即物质的量扩大a倍,则相应的广度函数便扩大a倍。
强度性质:强度性质的值只与系统自身的特点有关,与物质的量无关,如温度,压力,密度,摩尔体积等。
注:状态函数仅取决于系统所处的平衡状态,而与此状态的历史过程无关,一旦系统的状态确定,其所有的状态函数便都有唯一确定的值。
二、热力学第一定律热力学第一定律的数学表达式:对于一个微小的变化状态为:dU=公式说明:dU表示微小过程的内能变化,而δQ和δW则分别为微小过程的热和功。
它们之所以采用不同的符号,是为了区别dU是全微分,而δQ和δW不是微分。
或者说dU与过程无关而δQ和δW却与过程有关。
这里的W既包括体积功也包括非体积功。
以上两个式子便是热力学第一定律的数学表达式。
它们只能适用在非敞开系统,因为敞开系统与环境可以交换物质,物质的进出和外出必然会伴随着能量的增减,我们说热和功是能量的两种传递形式,显然这种说法对于敞开系统没有意义。
三、体积功的计算1.如果系统与环境之间有界面,系统的体积变化时,便克服外力做功。
将一定量的气体装入一个带有理想活塞的容器中,活塞上部施加外压。
当气体膨胀微小体积为dV时,活塞便向上移动微小距离dl,此微小过程中气体克服外力所做的功等于作用在活塞上推力F与活塞上移距离dl的乘积因为我们假设活塞没有质量和摩擦,所以此活塞实际上只代表系统与环境之间可以自由移动的界面。

物理化学知识点归纳物理化学是化学学科的一个重要分支,它综合运用物理学的原理和方法来研究化学现象和过程。
以下是对物理化学一些重要知识点的归纳:一、热力学第一定律热力学第一定律,也就是能量守恒定律,表明能量可以在不同形式之间转换,但总量保持不变。
在热力学中,通常用公式△U = Q + W来表示,其中△U 是系统内能的变化,Q 是系统吸收或放出的热量,W 是系统对外做功或外界对系统做功。
例如,在一个绝热容器中进行的化学反应,如果体系对外做功,那么内能就会减少;反之,如果外界对体系做功,内能就会增加。
二、热力学第二定律热力学第二定律有多种表述方式,其中克劳修斯表述为:热量不能自发地从低温物体传到高温物体。
开尔文表述为:不可能从单一热源取热使之完全变为有用功而不产生其他影响。
熵(S)的概念在热力学第二定律中至关重要。
对于一个孤立系统,熵总是增加的,这意味着系统总是朝着更加混乱和无序的方向发展。
比如,混合气体自发扩散后,不会自动分离回到初始状态,因为这个过程熵增加了。
三、热力学第三定律热力学第三定律指出,绝对零度(0K)时,纯物质完美晶体的熵值为零。
这一定律为计算物质在不同温度下的熵值提供了基准。
四、化学平衡化学平衡是指在一定条件下,可逆反应中正逆反应速率相等,反应物和生成物的浓度不再随时间改变的状态。
平衡常数(K)是衡量化学平衡的重要参数。
对于一个一般的化学反应 aA + bB ⇌ cC + dD,平衡常数 K 的表达式为:K = C^cD^d / A^aB^b (其中方括号表示物质的浓度)。
影响化学平衡的因素包括温度、浓度、压强等。
例如,对于吸热反应,升高温度会使平衡向正反应方向移动;增加反应物浓度,平衡也会向正反应方向移动。
五、相平衡相平衡研究的是多相体系中各相的组成、性质以及它们之间的相互转化规律。
相律是描述相平衡体系中自由度、组分数和相数之间关系的定律,其表达式为 F = C P + 2,其中 F 是自由度,C 是组分数,P 是相数。

物理化学热力学第一定律总结热力学第一定律是热力学中最基本的定律之一,并且与能量守恒原理密切相关。
它陈述了一个闭合系统内部的能量转换过程。
根据热力学第一定律,能量是不能从真空中产生的,也不能消失,它只能在系统内部进行转化。
该定律可以用以下公式表达:ΔU=Q-W其中,ΔU表示系统内部能量的变化,Q表示系统吸收的热量,W表示系统对外界做的功。
这个公式说明了能量的守恒,即系统吸收的热量和对外界做的功之和等于系统内部能量的变化。
当系统从外界吸收热量时,其内部能量会增加,而当系统对外界做功时,其内部能量会减少。
这种能量的转化是一个相互依存的过程,可以通过热力学第一定律进行描述。
热力学第一定律的应用十分广泛,并且在实际问题中具有重要的意义。
以下是热力学第一定律在不同领域的应用:1.在化学反应中,热力学第一定律可以用来计算反应的焓变。
通过测量反应前后系统吸收或释放的热量,可以计算出反应的焓变,从而了解反应的能量转化和方向。
2.在工程领域,热力学第一定律常用于能量转换设备的设计和优化中。
例如,蒸汽轮机、内燃机和制冷机等能量转换系统的效率可以通过热力学第一定律进行评估和计算。
3.在生物学领域,热力学第一定律可以用于研究生物体内的能量转化过程。
例如,通过测量生物体吸收的热量和对外界做的功,可以计算出生物代谢的能量转换效率。
热力学第一定律的重要性在于揭示了能量守恒的基本原理,为能量转化和能量利用提供了基础理论支持。
它对于研究和解决实际问题具有重要指导意义。
热力学第一定律的应用可以帮助我们评估能量转换过程的效率,优化能量利用方式,并促进可持续发展。
总之,物理化学热力学第一定律表述了能量守恒的原则,描述了能量转化和能量守恒的过程。
它在化学、工程、生物等领域具有广泛的应用,并对能量转换和利用提供了理论支持。
热力学第一定律的理解和应用可以帮助我们更好地理解能量转换过程,优化能量利用方式,并实现可持续发展的目标。

第一章 热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
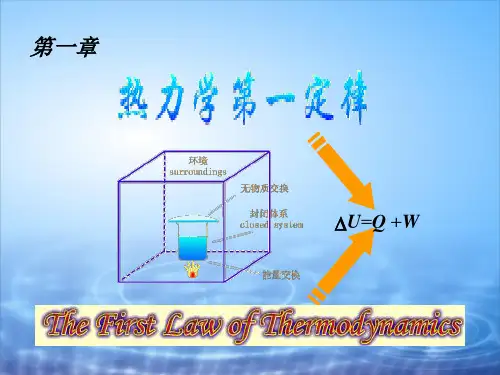
二、基本定律热力学第一定律:ΔU =Q +W 。
焦耳实验:ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式1、体积功的计算 δW = -p e d V恒外压过程:W = -p e ΔV可逆过程:1221ln ln p p nRT V V nRT W ==2、热效应、焓等容热:Q V =ΔU (封闭系统不作其他功) 等压热:Q p =ΔH (封闭系统不作其他功) 焓的定义:H =U +pV ; d H =d U +d(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂=定压热容与定容热容的关系:nR C C =-V p 热容与温度的关系:C p =a +bT +c’T 2 四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p e d V 等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V 可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程:Q =0 ; 利用C V (T 2-T 1)=-p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化:ΔH =Q =n Δ_H ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、热化学物质的标准态;热化学方程式;盖斯定律;标准摩尔生成焓。
摩尔反应热的求算:)298,()298(B H H m f B m r θθν∆=∆∑反应热与温度的关系—基尔霍夫定律:)(])([,p B C T H m p BB m r ∑=∂∆∂ν。


物理化学基础知识总结上册第一章热力学第一定律及其应用1.体系与环境:我们用观察,实验等方法进行科学研究时,必须先确定所要研究的对象,把一部分物质与其余的分开(可以是实际的,也可以是想像的)。
这种被划定的研究对象,就称为体系或系统,而在体系以外与体系密切相关,影响所能及的部分,则称为环境。
根据体系和环境之间的关系,可以把体系分为三种:体系完全不受环境的影响,和环境之间没有物质或能量的交换者,称为隔离体系或孤立体系;体系与环境之间没有物质的交换,但可以发生能量的交换者,称为封闭体系;体系不受上述限制,即体系与环境之间可以有能量以及物质交换者,称为敞开体系。
明确所研究的体系属于何种体系是至关重要的。
由于处理问题的对象不同,描述他们的变量不同,所适用的热力学公式也有所不同。
描述体系宏观性质的热力学变量可分为两类:广度性质(容量性质)和强度性质。
广度性质的数值与体系的数量成正比。
此种性质具有加和性,即整个性质的某种广度性质是体系中各部分该种性质的总和。
广度性质在数学上是一次齐函数。
强度性质此种性质不具有加和性,其数值取决于体系自身的特性,与体系的数量无关。
强度性质在数学上是零次齐函数。
体系的某种广度性质除以总质量或物质的量(或者把体系的两个容量性质相除)之后就成为强度性质。
若体系中所含物质的量是单位量,即一摩尔,则广度性质就成为强度性质。
2.热力学平衡态和状态函数:热平衡,力学平衡,相平衡,化学平衡。
当体系处于一定的状态时,其广度性质和强度性质都具有一定的数值。
但是体系的这些性质彼此之间是相互关联的,通常只需要指定其中的几个,其余的也就随之而定了。
也就是说,在这些性质之中只有部分是独立的。
体系的某些性质的改变只与始态和终态有关,而与变化时所经历的途径无关。
在热力学中,把具有这种特性的物理量叫做状态函数。
热和功与其改变的途径有关,是过程函数,从微观角度来说,功是大量质点以有序运动而传递的能量,热量是大量质点以无序运动方式而传递的能量。

物理化学知识点总结(热力学第一定律).doc物理化学知识点总结(热力学第一定律)摘要:热力学第一定律是热力学的基础之一,它描述了能量守恒的原理。
本文将对热力学第一定律进行详细的阐述,包括其定义、数学表达式、应用以及在物理化学中的重要作用。
关键词:热力学第一定律;能量守恒;物理化学;系统;状态函数一、引言热力学是研究能量转换和能量传递规律的科学。
热力学第一定律,也称为能量守恒定律,是理解和分析热力学过程的关键。
二、热力学第一定律的定义热力学第一定律指出,能量既不能被创造也不能被消灭,只能从一种形式转换为另一种形式,或者从一个系统转移到另一个系统。
在封闭系统中,能量的总量保持不变。
三、热力学第一定律的数学表达式对于一个封闭系统,热力学第一定律可以用以下数学表达式表示:[ \Delta U = Q - W ]其中,( \Delta U ) 是系统内能的变化,( Q ) 是系统吸收的热量,( W ) 是系统对外做的功。
四、系统与状态函数在热力学中,系统是指我们研究的对象,它可以是封闭的或开放的。
状态函数是描述系统状态的物理量,如温度、压力、体积等,它们只与系统的状态有关,而与系统状态变化的过程无关。
五、热力学第一定律的应用理想气体的等体过程在等体过程中,体积保持不变,系统对外不做功,热力学第一定律简化为 ( \Delta U = Q )。
理想气体的等压过程在等压过程中,压力保持不变,系统对外做膨胀功,热力学第一定律可以表示为 ( \Delta U = Q + W )。
理想气体的等温过程在等温过程中,温度保持不变,理想气体的内能不发生变化,热力学第一定律简化为 ( 0 = Q - W )。
六、热力学第一定律与能量转换热力学第一定律不仅适用于热能和机械能之间的转换,还适用于其他形式的能量,如电能、化学能等。
七、热力学第一定律在物理化学中的应用化学反应在化学反应中,热力学第一定律用于计算反应热,即反应过程中系统吸收或释放的热量。


物理化学大一知识点笔记一、热力学1. 热力学基本概念- 系统与环境- 状态函数与过程函数- 热力学第一定律2. 理想气体状态方程- 环境压强与气体压强- 环境温度与气体温度- 理想气体状态方程及其推导3. 内能、焓和焓变- 内能的定义和性质- 焓的定义和性质- 焓变与热量的关系4. 熵和熵变- 熵的定义和性质- 熵增原理- 熵变与热量的关系5. 等温、绝热过程- 等温过程的性质和示意图- 绝热过程的性质和示意图- 理想气体的等温、绝热过程公式6. 热力学循环- 闭合系统的热力学循环- 热机效率和制冷系数- 卡诺循环和卡诺定理二、化学反应动力学1. 反应速率与反应级数- 反应速率的定义和表达式- 反应级数与反应速率的关系- 零级、一级和二级反应速率方程2. 碰撞理论- 碰撞理论的基本思想- 反应物分子碰撞的能量、角动量要求- 碰撞理论与反应速率的关系3. 简单化学反应动力学公式- 推导简单化学反应速率方程- 求解反应速率常数和反应级数- 缓慢反应和快速反应的判断4. 温度对反应速率的影响- 温度对反应速率的影响规律- 阿伦尼乌斯方程及其应用- 活化能和反应速率常数的关系5. 反应速率与浓度的关系- 工程级数和动力学级数的定义与区别- 工程级数和动力学级数的计算方法- 浓度对反应速率的影响规律6. 反应平衡和化学平衡常数- 反应平衡的条件- 平衡常数的定义和性质- 平衡常数与反应热力学的关系三、电化学1. 电化学基本概念- 电解质与非电解质- 电解和电极- 电池和电解槽2. 电解过程- 电解过程的基本方程- 电解过程的质量和电荷关系- 电解过程的电动势和电压3. 电池和电池电势- 电池的基本构成和工作原理- 电池的电动势和电动势方程- 电池电势和标准氢电极的关系4. 氧化还原反应- 氧化还原反应的基本概念- 氧化还原反应的电子转移和离子转移- 氧化还原反应的电子转移系数5. 电化学动力学- 过电位和极化现象- 极化曲线和电解过程的动力学- 电化学反应的速率方程和电流效率6. 腐蚀与防护- 金属腐蚀的基本机理- 腐蚀速率与电流密度的关系- 防腐涂层和电阻涂层的应用以上是物理化学大一知识点的笔记,涵盖了热力学、化学反应动力学和电化学三个方面的基础概念和公式。
1第一章, 热力学第一定律 各知识点架构纲目图如下:及过程 溶解及混合 化学变化 相变化 热(Q ):系统与环境间由于温差而交换的能量。
是物质分子无序运动的结果。
是过程量。
功(W ):除热以外的,在系统与环境间交换的所有其它形式的能量。
是物质分子有序运动的结果,是过程量。
热力学能 (U ):又称为内能,是系统内部能量的总和。
是状态函数,且为广度量,但绝对值不知道。
热力学第一定律数学表达式:△U =Q +W ,在封闭系统,W 非=0,恒容条件下,△U =Q V 。
焓函数(H ):定义,H ≡U +pV , 是状态函数,且为广度量,但绝对值不知道。
在封闭系统,W 非=0,恒压条件下,△H =Q p 。
热力学第一定律及 焓函数系统与环境间交换能量 的计算(封闭 系统,W 非=0)简单的pTV 变化 理想气体(IG)系统:2211,,;T TV m p mT T U n C dT H n C dT ∆=∆=⎰⎰ 理想气体 恒温过程 焦尔实验:(1)结论:(∂U /∂V)T =0; (2)推论:U IG =f (T ); H IG =g (T ) △U =△H =0; W =-Q =2121ln /VVpdV nRT V V -=-⎰ (可逆)恒容过程:W =0;Q V =△U= 21,;TV mT n C dT ⎰绝热过程:Q =0;△U = W 不可逆(恒外压):nC V ,m (T 2-T 1)=-p 2(V 2-V 1) 可逆: 11,21112111()()1V m p V nC T T V V γγγγ---=-- Q p =△H =21,;T p m T n C dT ⎰W =-p 外(V 2-V 1); △U =△H -p △V (常压下,凝聚相:W ≈0;△U ≈△H )恒压过程: 节流膨胀:Q =0;△H =0;μJ-T =(d T /d p )H =0 T 不变(例如理想气体) <0致热 >0 致冷 相变化 △U =△H -p △VQ p =△H ; W =-p △V≈0,△U ≈△H (常压下凝聚态间相变化)=-nRT (气相视为IG) 相变焓与温度关系:2121,()()Tm m p mT H T H T C dT ββαα∆=∆+∆⎰化学变化 摩尔反应焓的定义:△r H m =△r H /△ξ 恒压反应热与恒容反应热的关系:△r H m =△r U m +∑νB (g)RT标准摩尔反应焓的计算:1B ()(B,)r m f mH T H T ν∆=∑∆!!反应进度定义、标准摩尔生成焓和标准摩尔燃烧焓的定义。
热一定律总结一、 通用公式ΔU = Q + W绝热: Q = 0,ΔU = W 恒容(W ’=0):W = 0,ΔU = Q V恒压(W ’=0):W =-p ΔV =-Δ(pV ),ΔU = Q -Δ(pV ) → ΔH = Q p 恒容+绝热(W ’=0) :ΔU = 0 恒压+绝热(W ’=0) :ΔH = 0焓的定义式:H = U + pV → ΔH = ΔU + Δ(pV )典型例题:3.11思考题第3题,第4题。
二、 理想气体的单纯pVT 变化恒温:ΔU = ΔH = 0变温: 或或 如恒容,ΔU = Q ,否则不一定相等。
如恒压,ΔH = Q ,否则不一定相等。
C p , m – C V , m = R双原子理想气体:C p , m = 7R /2, C V , m = 5R /2 单原子理想气体:C p , m = 5R /2, C V , m = 3R /2典型例题:3.18思考题第2,3,4题书2.18、2.19三、 凝聚态物质的ΔU 和ΔH 只和温度有关或典型例题:书2.15ΔU = n C V , md T T 2T1∫ ΔH = n C p, md T T2 T1∫ ΔU = nC V , m (T 2-T 1) ΔH = nC p, m (T 2-T 1)ΔU ≈ ΔH = nC p, m d T T 2T 1∫ΔU ≈ ΔH = nC p, m (T 2-T 1)四、可逆相变(一定温度T 和对应的p 下的相变,是恒压过程)ΔU ≈ ΔH –ΔnRT(Δn :气体摩尔数的变化量。
如凝聚态物质之间相变,如熔化、凝固、转晶等,则Δn = 0,ΔU ≈ ΔH 。
101.325 kPa 及其对应温度下的相变可以查表。
其它温度下的相变要设计状态函数不管是理想气体或凝聚态物质,ΔH 1和ΔH 3均仅为温度的函数,可以直接用C p,m计算。
或典型例题:3.18作业题第3题五、化学反应焓的计算其他温度:状态函数法Δ H m (T ) = ΔH 1 +Δ H m (T 0) + ΔH 3α ββ α Δ H m (T )α βΔH 1ΔH 3Δ H m (T 0)α β可逆相变298.15 K:ΔH = Q p = n Δ H m αβΔr H m ө =Δf H ө(生) – Δf H ө(反) = y Δf H m ө(Y) + z Δf H m ө(Z) – a Δf H m ө(A) – b Δf H m ө(B) Δr H m ө =Δc H ө(反) – Δc H ө(生) = a Δc H m ө(A) + b Δc H m ө(B) –y Δc H m ө(Y) – z Δc H m ө(Z)ΔH = nC p, m (T 2-T 1)ΔH = n C p, m d TT 2T1∫ΔU 和ΔH 的关系:ΔU = ΔH –ΔnRT (Δn :气体摩尔数的变化量。
1 热力学第一定律1.1 重点与难点严格区分状态函数与非状态函数(Q 、W ),并熟练掌握状态函数的数学特征 状态的定义,状态函数性质及数学特征。
体系始终态一旦确定,其状态函数改变量可通过设计途经而求算。
体系状态发生变化,其状态函数值可能发生变化,但并不一定全部状态函数都一定发生变化。
求算过程的热与功,不能随意设计途径。
唯有在特定条件下 Q,W 能与状态函数改变量相关联(如等压无其他功 Q p =ΔH ),才与途径无关。
体系状态函数具备五个数学特征。
1.1.1 热力学第一定律数学表达式及其在理想气体中的应用表达式()'V UQ W Q W W ∆=-=-+,只适用于封闭体系,随着条件变化,存在 ΔU 与 Q 、W 之间的转换关系。
一定量理想气体 U 和 H ,均决定于温度(但若有相变发生,或并非自始至终为理想气体,则不属此列)。
故它无论发生 p,V 怎样变化,只要有 T 变化,可直接引用2211T T vm pm T T U nC dTH nC dT∆=∆=⎰⎰或 。
弄清节流过程与绝热过程的区别。
明确理想气体绝热可逆过程方程与状态方程的实质;前者指某过程进行中各参量间的关系,后者指体系达平衡状态时各参量间的关系。
在 p ~V 图上绝热线的陡度比等温线的大,两线只能相交一点。
自同一始态出发,经绝热可逆与绝热不可逆过程是不能达到相同的终态,但计算绝热体积功时可用同一式:,1122,(1p m a V mC p V p V W C γγγ-==-为热容商,即)1.1.2 掌握比较热力学可逆过程与不可逆过程的定义,特点。
热力学第一定律在热化学中的应用热总值不变定律,意味着固定始终且指定同一条件(全部恒压,或全部恒容,决非恒压恒容混相)下,ΔH 或 ΔU 可自设计各步途径热值之加和而求算。
基尔霍夫(Kirchhoff)定律:()()2121T r m r m Tr pm H T H T C dT θθ∆=∆+⎰∆ 有积分号"∫"意指可逆,故中间若有相变,则另添加焓变值。
1.1 热力学第一定律1.1.1 热力学的研究对象1.热力学:研究能量相互转换过程中所遵循的规律的科学2.化学热力学:用热力学的基本原理来研究化学现象以及和化学有关的物理现象的科学3.研究的内容:研究化学变化的方向和限度。
4.热力学方法:研究对象是由大量质点(原子、分子、离子等)构成的宏观物质体系,所得结论是大量质点集体的平均行为,具有统计意义。
5.局限性:只能告诉我们在某种条件下,变化能否自动发生,发生后进行到什么程度,但不能告诉我们变化所需的时间以及具体的机理———可能性1.1.2 基本概念1.1.2.1 体系与环境1.体系: 所研究的对象。
(物系或系统)2.环境:体系以外并与体系密切相关的部分。
3. 体系分类:敞开体系: 体系与环境之间既有物质交换又有能量交换() 封闭体系: 体系与环境之间没有物质交换只有能量交换() 孤立体系: 体系与环境之间没有物质交换没有能量交换 ()1.1.2.2 状态与状态函数1. 状态:体系的物理性质和化学性质的综合表现状态函数:描述体系状态的性质注:(1)体系与环境的划分不绝对 (2)体系与环境的界面可以是实际存在的,也可以是虚拟的2. 状态函数的特点:A.状态一定,值一定;反之亦然B.异途同归,值变相等,周而复始,数值还原。
C.状态函数的微小变化是全微分,并且可积分D.状态函数代数运算的结果仍然是状态函数,如ρ=m/VE.状态函数之间存在着相互联系,如对于一定量的理想气体P、V、T之间存在下列关系PV=nRT说明:①定量纯物质均相体系或组成不变的多组分均相体系:只需两个独立改变的状态函数就能确定体系的状态②组成可变的多组分均相体系:除两个独立改变的状态函数之外,还需各组分的物质的量3. 状态函数的分类:根据状态函数与体系物质的量的关系,状态函数可以分为两类:广度性质:其数值与体系中物质的量成正比,具有加和性。
整个体系的该广度性质的数值,是组成体系的各部分该性质数值的总和强度性质:其数值与体系中物质的量无关,没有加和性。