材料力学扭转和剪切

一、拉（压）杆强度条件：--------（1）σmax =F NA≤[σ]二、（剪切）切应力条件和挤压强度条件1.切应力强度条件：τ--------（2）=F S A≤[τ]2.挤压强度条件：--------（3）σbs =F bsA bs ≤[σbs ]三、圆轴扭转时的强度和刚度条件1.扭转强度条件：-----------（4）τmax =TR I P=TW t≤[τ]----------------（5）W t =116πD³2.扭转刚度条件： -----------（6）ψmax =TGI p≤[ψ]----------------（7）I p =132πD 4四：弯曲正应力强度条件：------(8)σmax =M max ×y maxI Z=M max W Z≤[σ]符号释义：1. ：正应力 σ2. τ：切应力3.T ：扭矩4.：轴力 F N 5.：剪切力 F S 6. F bs ：挤压力7.A ：剪切截面面积8. ：抗扭截面系数W t 9. ：横截面对圆心的极惯性矩 I p 10.y: 正应力到中性轴的距离11.ε：正应变(线应变)三个弹性材料的关系：1.E ：弹性模量（GN/m²）E =σε=tanα2. μ：为泊松比（钢材的μ为0.25-0.33）3.G ：剪切弹性模量（GN/m²）G =γτG =E2（1+μ）剪切胡可定律：τ=Gγ16.E ：抗拉刚度I p 17.胡可定律：σ=Eεσ=E y ρ18.ρ：曲率半径19. ：梁弯曲变形后的曲率 1ρ1ρ=MEI Z20.M ：弯矩21. ：外力偶矩M e12.γ：切应变(角应变)13.EA：抗拉强度(钢材的EA约为200GPa)14.δ：断后伸长率15.ψ：断面收缩率/相对扭转角F N F S梁受力有：轴力、剪切力和弯矩M。

一、材料力学的几个基本感念1.构件：工程结构或机械的每一组成部分。

材料力学中的四种基本变形举例
材料力学是研究材料在外力作用下的变形和破坏行为的学科，其中变
形是材料力学中的重要研究对象。

材料在受到外力作用时，会发生各
种形式的变形，其中最常见的四种基本变形包括拉伸变形、剪切变形、扭转变形和压缩变形。

一、拉伸变形
拉伸变形是指某个物体在受到外拉力作用时，其长度沿着外力方向发
生增加的现象。

例如，当我们把一根橡皮筋两端分别固定在两个支架上，并对其施加外拉力时，橡皮筋就会发生拉伸变形。

二、剪切变形
剪切变形是指某个物体在受到剪切应力作用时，其内部不同位置之间
产生相对错位或滑动的现象。

例如，在我们使用剪刀剪纸时，纸张就
会发生剪切变形。

三、扭转变形
扭转变形是指某个物体在受到扭矩作用时，在其截面内不同位置之间
产生相对错位或旋转的现象。

例如，在我们使用螺丝钉旋入木板时，螺丝钉就会发生扭转变形。

四、压缩变形
压缩变形是指某个物体在受到外压力作用时，其体积沿着外力方向发生减小的现象。

例如，在我们使用千斤顶压实土壤时，土壤就会发生压缩变形。

总之，以上四种基本变形是材料力学中最常见的变形类型，它们在材料工程领域中有着广泛的应用和研究。

了解这些基本变形类型对于深入理解材料的性能和行为具有重要意义。

一、拉（压）杆强度条件：--------（1）二、（剪切）切应力条件和挤压强度条件1.切应力强度条件：τ --------（2）2.挤压强度条件：--------（3）三、圆轴扭转时的强度和刚度条件资料个人收集整理，勿做商业用途1.扭转强度条件：-----------（4）----------------（5）2.扭转刚度条件：-----------（6）----------------（7）四：弯曲正应力强度条件：------(8)符号释义：1.：正应力2. τ：切应力3.T：扭矩4.：轴力5.：剪切力6.7.A：剪切截面面积8.：抗扭截面系数9.：横截面对圆心的极惯性矩10.y: 正应力到中性轴的距离11.ε：正应变(线应变) 三个弹性材料的关系：1.E：弹性模量（GN/m²）2. μ：为泊松比（钢材的μ为0.25-0.33）3.G：剪切弹性模量（GN/m²）剪切胡可定律：τ=Gγ16.E：抗拉刚度17.胡可定律：σ=Eεσ=E18.ρ：曲率半径19.：梁弯曲变形后的曲率20.M：弯矩轴力、剪切力、均为内力求内力的方法-截面法：1.假想沿m-m横截面将杆件切开2.留下左半端或右半段3.将弃去部分对留下部分的作用(力)用内力代替4.对留下部分写平衡方程，求出内力的值。

当你选择好研究对象时，建立坐标系，这个对象的所有受力的x方向的代数和，和y方向的代数和为零，这就建立平衡方程，【me=o】，就是你在研究对象上选取一个点作为支点，然后所有力对这个点取矩，顺时针和逆时针方向的代数和为零，这样就分别建立三个平衡方程，可以联立接触其中未知数，这种情况只是用于解决静定结构的。

12.γ：切应变(角应变)21.：外力偶矩13.EA：抗拉强度(钢材的EA约为200GPa)14.δ：断后伸长率15.ψ：断面收缩率/相对扭转角梁受力有：轴力、剪切力和弯矩M。

一、材料力学的几个基本感念1.构件：工程结构或机械的每一组成部分。

浅析材料力学四种基本变形的异同点公主岭市职业教育中心宋静辉机械基础高等教育中材料力学的研究范围主要限于杆件，即长度远大于宽度和厚度的构件。

作用远杆件上的外力有各种形式，但杆件的基本变形形式只有四种：拉伸或压缩（简称拉压）、剪切、扭转和弯曲。

这四种基本变形是材料力学的重点内容，构成了材料力学理论体系中的一个个独立部分，学生学习时后很容易混淆。

现分析和总结四种基本变形的异同点，便于学生学习和理解。

一、四种变形的不同点1.受力特点不同。

受拉伸或压缩的构件大多是等截面直杆，其受力特点是：作用在杆端的两外力（或外力的全力）大小相等，方向相反，力的作用线与杆件的轴线重合。

工程中的连接件（如铆钉、螺栓等）会发生剪切变形，其受力特点是：作用的构件两侧面上外力的全力大小相等，作用线平行且相距很近；另外，承受剪切作用的连接件在传力的接触面上同时还受挤压力作用。

机械中的轴类零件往往产生扭转变形，其受力特点是：在垂直于轴线的平面内，作用着一对大小相等、方向相反的力偶。

梁是机器设备和工程结构中最重要的构件，主要发生弯曲变形，其受力特点是:作用在梁上的外边与其轴线垂直.若这些外力只是一对等值反向的力偶时,则称为纯弯曲。

2.变形特点不同。

构件在外力作用下发生的几何形状和尺寸变化称为变形。

拉压变形的特点是杆件沿轴线方向伸长或缩短；剪切变形的变形特点是介于两作用之间的各截面有沿作用力方向发生相对错动的趋势；扭转变形的变形特点是轴的各截面绕轴线将由直线变成曲线。

3.内力不同。

物体内某一部分与另一部分间相互作用的力称为内力。

构件在受到外力作用的同时，其内部将产生相应的内力。

对于发生拉压变形的杠件，内力遍及整个杆体内部，因为外力的作用线与杆件的轴线重合，故分布内力的合力作用线也必与杆件轴线重合，这种内力称为轴力。

轴力或为拉力或为压力。

构件受剪切时的内力称为剪刀，剪力分布在剪切面上（受剪件中发生相对错动的截面），其分布比较复杂，在工程实力是一个截面平面内的力偶，其力偶矩称为截面上的扭矩。

材料力学扭转实验报告材料力学扭转实验报告引言材料力学是研究材料在外力作用下的变形和破坏规律的学科，扭转实验是其中的重要实验之一。

本报告旨在介绍材料力学扭转实验的原理、方法、实验装置以及实验结果的分析与讨论。

实验原理扭转实验是通过施加一个力矩来引起材料的扭转变形，从而研究材料的力学性能。

在扭转实验中，材料会发生剪切应变，而剪切应力与剪切应变之间的关系可以通过剪切模量来描述。

剪切模量是材料的一项重要力学参数，它反映了材料抵抗剪切变形的能力。

实验方法本次实验采用了经典的圆柱体扭转实验方法。

首先，选择一根具有一定长度的圆柱体样品，将其固定在扭转实验机上。

然后，通过扭转实验机施加一个力矩，使样品发生扭转变形。

同时，通过测量扭转角度和施加力矩的大小，可以得到材料的剪切模量。

实验装置本次实验所用的扭转实验装置包括扭转实验机、样品夹具、测量仪器等。

扭转实验机是用来施加力矩的设备，样品夹具用于固定样品，并保证其能够自由扭转。

测量仪器包括扭转角度测量仪和力矩测量仪，用于测量样品的扭转角度和施加的力矩。

实验结果分析与讨论通过实验测量得到的扭转角度和施加的力矩数据可以用来计算材料的剪切模量。

根据材料力学的理论知识，剪切模量可以通过以下公式计算：G = (L * T) / (J * θ)其中，G表示剪切模量，L表示样品的长度，T表示施加的力矩，J表示样品的截面转动惯量，θ表示样品的扭转角度。

通过对实验数据的处理和计算，可以得到材料的剪切模量。

进一步地，可以通过对不同材料进行扭转实验，比较其剪切模量的大小，从而分析不同材料的力学性能。

结论通过本次材料力学扭转实验，我们了解了扭转实验的原理和方法，并通过实验装置和测量仪器进行了实验。

通过对实验数据的分析和计算，我们得到了材料的剪切模量，并通过比较不同材料的剪切模量，进一步了解了材料的力学性能。

这对于我们深入了解材料的性质和应用具有重要意义。

总结材料力学扭转实验是研究材料力学性能的重要实验之一。

材料力学扭转切应力计算公式材料的力学性质是表征其对外力作用的响应能力的重要指标。

扭转切应力是材料在受到扭转力矩作用时所产生的应力。

在许多工程和科学研究中，通过计算和测量扭转切应力可以获得材料的力学性能参数，如剪切模量和剪切强度等。

在材料力学中，扭转切应力计算公式主要有两种形式：切应力公式和剪切应力公式。

1.切应力公式：切应力（Shear Stress）指材料内部产生的由于外力而对于材料内部其中一剖面的剪切应力。

一般情况下，切应力可以采用切应力图形表示。

τ=T/S其中，τ是切应力，T是扭转力矩，S是截面积。

切应力的单位一般是帕斯卡（Pa）或兆帕（MPa）。

在实际应用中，我们常常会遇到不同形状的材料，如圆形、方形、矩形等。

对于这些不同形状的截面，切应力的计算公式也有所不同。

对于圆截面，切应力的计算公式为：τ=T/(π*r^2)对于矩形截面，切应力的计算公式为：τ=T/(b*h)其中，b是矩形截面的宽度，h是矩形截面的高度。

2.剪切应力公式：剪切应力（Shear Strain）是材料在受到剪切力作用时所产生的应变。

在扭转切应力的计算中，剪切应力是切应力的一个重要参数。

剪切应力的计算公式如下：γ=θ*h/l其中，γ是剪切应力，θ是材料的扭转角度，h是扭转试样的高度，l是扭转试样的长度。

剪切应力可以用来计算材料的剪切模量（Shear Modulus），剪切模量可以通过下式计算得到：G=τ/γ其中，G是剪切模量。

综上所述，材料力学扭转切应力计算公式主要有切应力公式和剪切应力公式，通过这些公式可以计算得到材料的扭转切应力、剪切模量等力学性能参数。

这些参数可以用于工程设计和科学研究中，帮助人们了解材料的力学性能和应用范围。

材料力学扭转实验报告1. 实验目的。

本实验旨在通过扭转实验，探究材料在扭转加载下的力学性能，了解材料的剪切模量和剪切应力等参数。

2. 实验原理。

材料在扭转加载下，内部会产生剪切应力，而材料的剪切模量则是描述材料在扭转加载下的变形特性的重要参数。

通过扭转实验，可以测定材料的剪切模量和剪切应力，进而了解材料的力学性能。

3. 实验装置。

本实验采用了扭转实验机，实验样品为圆柱形，实验过程中需要测量扭转角度和扭转力矩。

4. 实验步骤。

（1）将实验样品装入扭转实验机，并调整好实验参数。

（2）施加扭转力矩，记录下扭转角度和扭转力矩的变化。

（3）根据实验数据，计算出材料的剪切模量和剪切应力。

5. 实验数据处理。

通过实验数据的处理，得到了材料的剪切模量和剪切应力的数值，进一步分析了材料在扭转加载下的力学性能。

6. 实验结果分析。

根据实验结果，我们可以得出材料在扭转加载下的剪切模量为xx，剪切应力为xx，进一步分析了材料的力学性能。

7. 实验结论。

通过本次实验，我们成功测定了材料在扭转加载下的剪切模量和剪切应力，了解了材料在扭转加载下的力学性能特点。

8. 实验总结。

本实验通过扭转实验，深入探究了材料在扭转加载下的力学性能，对材料力学的研究具有一定的指导意义。

9. 参考文献。

[1] 张三, 材料力学导论, 北京大学出版社, 2005.[2] 李四, 材料力学实验指导, 清华大学出版社, 2008.10. 致谢。

感谢实验室的老师和同学们在实验过程中的帮助和支持。

以上为本次材料力学扭转实验报告的全部内容。

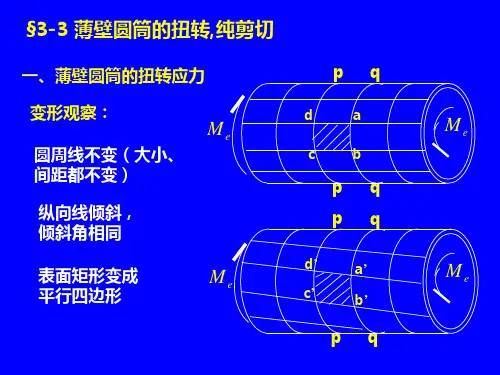
第3章 扭转1、扭转的概念：杆件的两端个作用一个力偶，其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线，致使杆件的任意两个横截面都发生绕轴线的相对转动，即为扭转变形。

2、外力偶矩的计算{}{}{}min /95491000602r KW m N e e n P M P M n=⇒⨯=⨯⨯⋅π 式中，e M 为外力偶矩。

又由截面法：e e M T M T =⇒=-0 T 称为n n -截面上的扭矩。

规定：若按右手螺旋法则把T 表示为矢量，当矢量方向与研究部分中截面的外法线的方向一致时，T 为正；反之为负。

3、纯剪切（1）薄壁圆筒扭转时的切应力 δπττδπ222r M r r M ee =⇒••=（2）切应力互等定理：在单元体相互垂直的两个平面上，切应力必然成对存在，且数值相等；两者都垂直于平面的交线，方向则共同指向或背离这一交线。

（3）切应变 剪切胡克定律：当切应力不超过材料的剪切比例极限时，切应变γ与切应力τ成正比。

γτG = G 为比例常数，称为材料的切变模量。

弹性模量E 、泊松比μ和切变模量G 存在关系：)1(2μ+=EG 4、圆轴扭转时的应力（1）变形几何关系：距圆心为ρ处的切应变为dxd ϕργρ=（2）物理关系：ρτ为横截面上距圆心为ρ处的切应力。

dxd G G ϕρτγτρρρ=⇒= （3）静力关系：内力系对圆心的力矩就是横截面的扭矩：dA d d GdA T AxA⎰⎰==2ρρτϕρ 以p I 表示上式右端的积分式：dA I Ap ⎰=2ρ p I 称为横截面对圆心O 点的极惯性矩（截面二次极矩）横截面上距圆心为ρ的任意点的切应力：pI T ρτρ=ρ最大时为R ，得最大切应力：pI TR =max τ引用记号RI W p t =t W 称为抗扭截面系数。

则tW T =max τp I 和t W 的计算（1）实心轴：3224420032D R d d dA I RAp ππθρρρπ====⎰⎰⎰16233D R RI W p t ππ===（2）空心轴：)1(32)(324444202/2/32αππθρρρπ-=-===⎰⎰⎰D d D d d dA I D d Ap)1(16)(164344αππ-=-==D d D DRI W p t5、圆轴扭转时的变形pGI Tl =ϕ ϕ为扭转角，l 为两横截面间的距离。

材料力学中的四种基本变形举例
1.拉伸变形：
拉伸变形是指在外力的作用下，物体的长度增加或变长的过程。

这种
变形常见于拉伸试验中的拉力加载中，例如在拉伸试验机上施加外力，拉
伸材料直至材料的断裂点。

一个常见的例子是橡皮筋，当我们拉伸橡皮筋时，它的长度会增加。

2.压缩变形：
压缩变形是指在外力的作用下，物体的长度减少或变短的过程。

这种
变形常见于承受压力的构件中，例如梁柱结构承受竖向荷载时会产生压缩
变形。

一个典型的例子是弹簧，当我们用力将弹簧压缩时，它的长度会变短。

3.剪切变形：
剪切变形是指在外力的作用下，物体的平行侧面发生相对位移的过程。

这种变形常见于切削和金属加工中，例如在使用剪切机切割金属板材时，
金属板材的平行侧面会产生相对的移动。

另一个例子是在泥土工程中，当
土壤受到剪切力时，会发生剪切变形。

4.扭转变形：
扭转变形是指在外力作用下，物体沿纵轴发生旋转的过程。

这种变形
常见于旋转机械中，例如在使用螺旋桨驱动船只前进时，船体会发生扭转
变形。

另一个例子是在汽车悬挂系统中，当车辆转弯时，车身会发生扭转
变形。

这四种基本变形在材料力学中都具有重要的意义，并广泛应用于工程设计和材料选型过程中。

通过对这些变形的认识和理解，我们能够更好地预测和控制材料的行为和性能。