材料力学-剪切

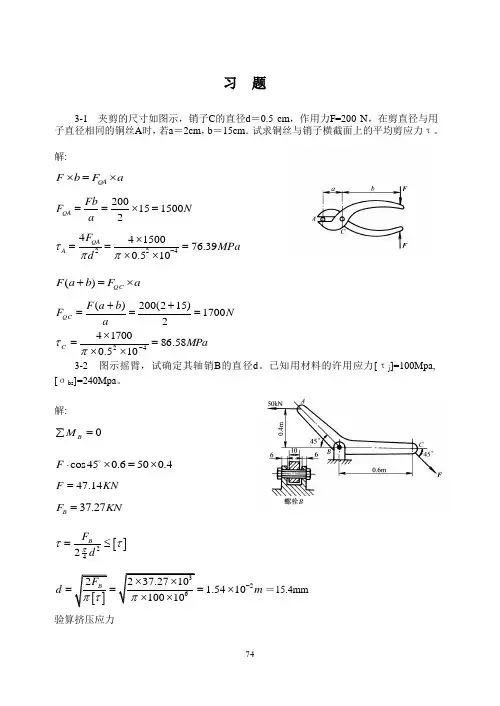
习 题3-1 夹剪的尺寸如图示，销子C 的直径d ＝0.5 cm ，作用力F=200 N ，在剪直径与用子直径相同的铜丝A 时，若a ＝2cm ，b ＝15cm ．试求铜丝与销子横截面上的平均剪应力τ。

解:QA F b F a ⨯=⨯ 2001515002QA Fb F N a ==⨯= 22444150076.390.510QAA F MPa d τππ-⨯===⨯⨯ ()QC F a b F a +=⨯()200(215)17002QC F a b F N a ++=== MPa C 58.86105.01700442=⨯⨯⨯=-πτ 3-2 图示摇臂，试确定其轴销B 的直径d 。

已知用材料的许用应力[τj ]=100Mpa,[σbs ]=240Mpa 。

解:0=∑B Mcos450.6500.4F ⋅⨯=⨯47.14F KN =37.27B F KN =[]242B F d πττ=≤ []3262237.2710 1.541010010B F d m πτπ-⨯⨯===⨯⨯⨯＝15.4mm 验算挤压应力[]32237.27102421.5410110B bs bs bs F MPa A σσ--⨯===≈⨯⨯⨯ 3-3 图示直径为 d 的拉杆，其端头的直径为D ，高度为h ，试建立 D 、h 与d 的合理比值（从强度考虑）。

已知：[σ]＝120 MPa ，[τj ]＝90 MPa ，[σbs ]＝240 MPa ．解:[]310030.14-⨯==P Pd σπ []jy p d D σππ=-2244310261.1-⨯=P D[]310717.12-⨯==P d P h τπ ∴67.1:22.1:1::=h D d 3－4 两根矩形截面木杆，用两块钢板连接在一起，受轴向载荷P ＝45kN 作用。

已知截面宽度 b ＝25 cm ，沿材的顺纹方向，许用拉应力[σ]＝6MPa ，许用挤压应力[σjy ]＝10 MPa ，许用剪应力[τj ]＝1MPa ，试确定接头的尺寸δ、l 和 h 。

剪切中心与牵连位移1.剪切中心剪切中心又叫扭转中心、弯曲中心，基本概念为截面合力线如果经过该点，那么将只会发生弯曲而不会发生扭转。

这里要区分一下形心与剪切中心，一般情况下这两者不是同一点，但是如果截面有两根以上的对称轴时，那么二者重合，如圆、矩形、对称工字型。

那么如何去求解一个截面的剪切中心呢？基本过程有两步：（1）绘制出无扭转时截面的切应力分布规律；（2）利用应力与内力之间的关系列静力学方程进行求解一般来说，很多同学对第一个步骤掌握不到位，不清楚截面在受剪时切应力的分布。

所以有必要给大家列出一些常用截面的切应力分布规律。

如下图所示：图1：常见薄壁杆件的切应力分布规律和剪切中心位置注图1中S 表示剪切中心，C 表示形心知道了切应力的分布规律，那么就可以根据静力学关系进行求解了。

静力学关系公式如下：P dA F A s ==⎰τ0==⎰A dA d T τ截面扭转为0，截面合剪力为P 。

从图1中的截面切应力分布规律我们可以得出如下结论：（1）剪力中心是截面特性，与外荷载无关；（2）薄壁杆件开口杆件与闭口杆件的切应力分布有区别（有兴趣的同学可以查资料）（3）薄壁杆件的切应力分布与受力荷载有关。

下面我们来看一个算例：上图非对称工字型薄壁钢受水平力P ，求作用何处是无扭转产生。

很明显，需要求剪切中心，那么可以按照下图的计算模型进行计算：顶板承担剪力1s F ，底板承担剪力2s F 。

根据静力学关系有：P F F s s =+21()021=--e h F e F s s对上下顶板的最大切应力分别从整体和单独一块板应力切应力公式有： 顶板最大切应力I S P I S F s ⨯⨯=⨯⨯=δδτ11111max ；底板最大切应力IS P I S F s ⨯⨯=⨯⨯=δδτ22221max 其中21I I 、分别为上下顶板的惯性矩，且有21I I I +=。

故而： I I P F s 11⨯=，II P F s 22⨯= 所以：h I I h I e e h e I I 9821121=+=⇒-=（结论：剪切中心与上下板的刚度比有关） 2. 牵连位移这里主要讨论一下支座链杆的位移对杆件的影响。

剪切应变的定义剪切应变是材料力学中的重要概念之一，用于描述材料在外力作用下的形变程度。

剪切应变的定义可以通过考虑材料内部的相对位移来进行说明。

在材料力学中，剪切应变是指材料内部不同位置的相对位移与材料长度之比。

剪切应变的定义可以通过考虑材料的几何形状和变形情况来进行解释。

当材料受到作用力时，力的作用方向与材料的纵向方向不一致，这就会引起材料的形变。

剪切应变的产生是由于材料内部不同位置之间的相对位移不同，即材料内部的相对位移具有梯度。

剪切应变的大小与材料内部相对位移的大小有关，相对位移越大，剪切应变也越大。

剪切应变可以通过材料的切变变形来进行解释。

当材料受到剪切力时，材料内部的相对位移会导致材料的形变。

材料的切变变形是指材料内部的平行层面之间的相对位移。

在材料受到剪切力作用时，材料内部的相对位移会导致材料的平行层面发生相对位移，从而引起材料的切变变形。

剪切应变的大小与材料的切变变形有关，切变变形越大，剪切应变也越大。

剪切应变的计算可以通过材料的几何形状和变形情况来进行。

在材料力学中，剪切应变可以通过材料内部相对位移的大小和材料长度之比来计算。

根据剪切应变的定义，可以得到剪切应变的计算公式。

通过对材料的形变情况进行分析，可以得到材料的剪切应变分布图。

剪切应变分布图可以用来描述材料的切变变形情况，从而得到材料的剪切应变分布情况。

剪切应变的性质可以通过材料的力学性质和变形情况来进行研究。

在材料力学中，剪切应变是描述材料形变程度的重要参数之一。

剪切应变的大小与材料的力学性质有关，不同材料的剪切应变性质不同。

通过对材料的剪切应变性质进行研究，可以得到材料的力学性质和变形情况。

剪切应变在工程实践中具有重要的应用价值。

在工程设计和材料选择中，剪切应变是评估材料力学性能的重要参数之一。

通过对材料的剪切应变进行分析，可以得到材料的剪切应变性能和变形情况。

对于需要承受剪切力的结构和材料，设计和选择具有良好剪切应变性能的材料是非常重要的。