优化与最优控制中的计算方法(叶庆凯,王肇明编著)思维导图
- 格式:xmin
- 大小:5.75 KB
- 文档页数:1




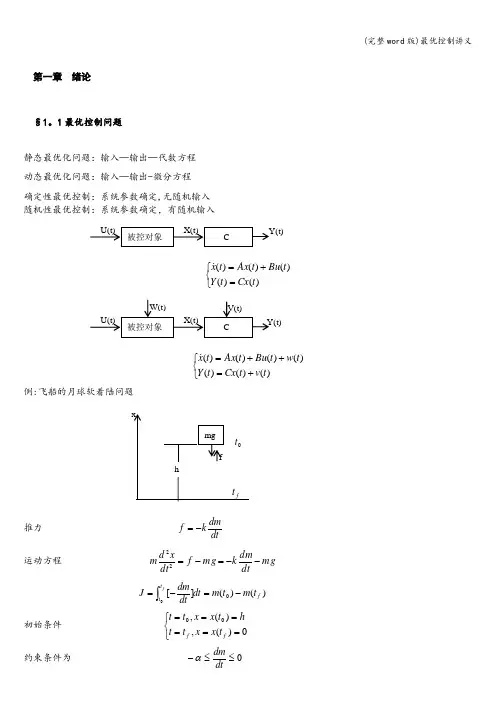
第一章 绪论§1。
1最优控制问题静态最优化问题:输入—输出—代数方程 动态最优化问题:输入—输出-微分方程 确定性最优控制:系统参数确定,无随机输入 随机性最优控制:系统参数确定,有随机输入⎩⎨⎧=+=)()()()()(t Cx t Y t Bu t Ax t x⎩⎨⎧+=++=)()()()()()()(t v t Cx t Y t w t Bu t Ax t x例:飞船的月球软着陆问题推力 dtdmkf -= 运动方程 mg dt dmk mg f dtx d m --=-=22 )()(][00f t t t m t m dt dtdmJ f-=-=⎰ 初始条件 ⎩⎨⎧======0)(,)(,00f f t x x t t ht x x t t约束条件为 0≤≤-dtdmα求min J§1.2最优控制的数学模型一 控制系统的数学模型(集中参数系统)直接法建立:动力学、运动学的基本定律,即解析法.间接法建立:通过“辩识"的途径确定系统的结构与参数.)),(),(()(t t u t x f t x= 其中 T n t x t x t x t x )](,)(),([)(21 =,T r t u t u t u t u )](,)(),([)(21 =,],,[21n f f f f = )(t x 为n 维状态向量,)(t u 为r 维控制向量,f 为n 维函数向量。
二 目标集通过)(t u 使)(t x 由)(0t x 到)(f t x ,其中)(0t x 为初始状态,并且通常为已知;)(f t x 为终端状态,即控制所要求达到的目标。
一般来说对终端状态的要求可用如下的约束条件表示:0)),((,0)),((21≤=f f f f t t x g t t x g 。
三 容许控制i u 具有不同的物理属性,一般有r 1,2i u i ,,=≤α,即在控制域U 内。