网络计划法 例题
- 格式:ppt
- 大小:243.00 KB
- 文档页数:103
2022-07-04 11:47 来源:打印| 收藏 |字号分享到:( )。
A.循环回路B.多个起点节点C.多个终点节点D.一对节点编号代表多项工作E.节点编号顺序错误【正确答案】 CDE【答案解析】选项C,有 8、9 两个终点节点,故错误;选项D,错在一对节点(1和 3) 表示了两项工作(B.C 工作);选项 E,节点 3、4 编号顺序错误。
参见教材 P117、119( )。
A.网络图必须正确表达各工作间的逻辑关系B.网络图中可以浮现循环回路C.网络图中一个节点惟独一条箭线引出D.网络图中严禁浮现没有箭头节点或者没有箭尾节点的箭线E.单目标网络计划惟独一个起点节点和一个终点节点【正确答案】 ADE【答案解析】双代号网络计划的绘图规则包括:①双代号网络图必须正确表达已定的逻辑关系;②双代号网络图中,严禁浮现循环回路;③双代号网络图中,在节点之间严禁浮现带双向箭头或者无箭头的连线;④双代号网络图中,严禁浮现没有箭头节点或者没有箭尾节点的箭线;⑤当双代号网络图的某些节点有多条外向箭线或者多条内向箭线时,为使图形简洁,可使用母线法绘制(但应满足一项工作用一条箭线和相应的一对节点表示);⑥绘制网络图时,箭线不宜交叉。
当交叉不可避免时,可用过桥法或者指向法;⑦双代号网络图中应惟独一个起点节点和一个终点节点(多目标网络计划除外),而其他所有节点均应是中间节点;⑧双代号网络图应条理清晰,布局合理。
参见教材P117、119网络图是( )。
工作紧前工作A .A 图B .B 图C .C 图D .D 图A B————CADA、BEDFC、D【正确答案】 C【答案解析】按双代号网络计划的绘图规则即可得出正确答案为C.参见教材 P117、119( )。
A.该工作的自由时差B.该工作的总时差C.该工作与其紧前工作之间的时间间隔D.该工作与其紧前工作之间的时距【正确答案】 A【答案解析】双代号时标网络计划中箭线上的波形线表示工作的自由时差。

工程网络计划有关时间参数的计算典型例题第一篇:工程网络计划有关时间参数的计算典型例题工程网络计划有关时间参数的计算典型例题例题1:某工程双代号网络计划如下图所示(单位:天)。
该网络计划的关键线路为()。
A.①→③→⑤→⑥B.①→③→④→⑤→⑥和①→②→③→④→⑤→⑥C.①→②→⑤→⑥和①→②→③→④→⑥D.①→②→③→⑤→⑥【正确答案】B【答案解析】按工作计算法可知,总工期为14天,关键线路为:①→③→④→⑤→⑥和①→②→③→④→⑤→⑥两条。
参见教材P128.例题2:[背景资料]某施工企业与业主签订了某工程的施工承包合同。
经监理工程师审核批准的施工进度计划如下图所示(时间单位:天)。
根据上述背景资料,回答下列第1~4小题:第1小题:双代号网络图中虚箭线表示()。
A.资源消耗程度B.工作的持续时间C.工作之间的逻辑关系D.非关键工作【正确答案】C【答案解析】在双代号网络图中,为了正确地表达图中工作之间的逻辑关系,往往需要用虚箭线。
虚线是实际工作中并不存在的一项虚设工作,故它们既不占用时间,也不消耗资源。
在双代号网络图中,任意一条实箭线都要占用时间、消耗资源。
参见教材P116.第2小题:监理工程师审核批准的施工进度计划工期是()天。
A.210B.245C.280【正确答案】D【答案解析】本题实质就是计算该网络计划的工期。
计算得到的最早开始时间、最早完成时间、最迟开始时间、最迟完成时间、总时差和自由时差。
由图可知计划工期是300天。
由于该网络计划图较简单,也可以分别计算四条线路的持续时间,关键线路的长就是计划工期。
参见教材P127.工期泛指完成任务所需要的时间,一般有以下3种;(1)计算工期,根据网络计划时间参数计算出来的工期,用T c 表示;(2)要求工期,任务委托人所要求的工期,用Tr表示;(3)计划工期,根据要求工期和计算工期所确定的作为实施目标的工期,用Tp表示。
网络计划的计划工期Tp应按下列情况分别确定:当已规定了要求工期Tr时,Tp≤Tr ;当未规定要求工期时,可令计划工期等于计算工期,Tp=Tr。

网络计划的练习题1.是非题1)关键线路是该网络计划中最长的线路,一个网络计划只有一条关键线路。
(×)2)时标网络计划的特点是可直接在网络图上看出各项工作的开始和结束时间。
(√)3)网络计划的工期优化,就是通过压缩网络中全部工作的持续时间,以达到缩短工期的目的。
(×)4)在网络计划执行过程中,关键工作的拖延将导致计划总工期不能实现,这时候对网络计划调整的方法只能是短某些工作的持续时间。
(×)5)双代号网络图组成要素中,把消耗时间、不消耗资源的工序,称作“虚工序”。
(×)6)网络计划工期优化的方法之一是将各项工作持续时间压缩。
(×)7)有时间坐标的网络图既适用于双代号网络,也可用于单代号网络。
(×)8)关键线路上的工作都是关键工作,非关键线路上的工作都是非关键工作。
(×)9)若工作的进度偏差小于自由时差,说明此对后续工作无影响,原计划可不作调整。
(√)10)若工作的进度偏差大于自由时差,说明此对后续工作有影响,原计划必须全部调整。
(×)11)网络计划的工期优化,就是通过压缩某些关键工作的持续时间,以达到缩短工期的目的。
(√)12)网络计划的工期优化,就是通过压缩网络中全部工作的持续时间,以达到缩短工期的目的。
(×)13)网络计划工期调整的方法,就是缩短某些工作的持续时间。
(×)14)网络计划中某项工作总时差时为零则自由时差必为零。
(√)15)网络计划中关键工作的总时差必为零。
(×)16)香蕉型曲线是由两种s曲线组合成的闭合曲线。
(√)17)关键工作进度落后必定影响工期。
(√)18)网络计划任何工作实际进度比计划进度落后必定影响工期。
(×)19)网络计划工期优化的方法之一是将各项工作持续时间压缩。
(×)20)有时间坐标的网络图既适用于双代号网络,也可用于单代号网络。
(×)21)搭接网络图既适用于双代号网络,也可用于单代号网络。

网络计划图例题在项目管理中,网络计划图是一种用于展示项目活动之间逻辑关系的图形化工具。
它可以帮助项目团队清晰地了解项目活动的先后顺序、持续时间和关键路径,从而更好地进行项目进度管理和资源分配。
下面我们通过一个具体的例子来学习网络计划图的绘制方法和应用技巧。
假设某公司要开展一项新产品的研发项目,项目包括需求分析、设计、开发、测试和上线等阶段。
我们可以根据这些活动之间的依赖关系来绘制网络计划图。
首先,我们需要确定各个活动的持续时间。
比如,需求分析可能需要5天,设计需要8天,开发需要15天,测试需要10天,上线需要3天。
然后,我们需要确定各个活动之间的依赖关系。
在这个例子中,设计活动必须在需求分析完成后开始,开发活动必须在设计完成后开始,测试活动必须在开发完成后开始,上线活动必须在测试完成后开始。
接下来,我们可以开始绘制网络计划图。
首先,在纵轴上标注出项目活动的名称,横轴上标注出项目活动的持续时间。
然后,根据活动之间的依赖关系,用箭头连接各个活动,箭头的方向表示活动的先后顺序,箭头的长度表示活动的持续时间。
最后,我们可以标注出关键路径,即项目完成所需的最短时间路径。
通过绘制网络计划图,我们可以清晰地看到各个活动之间的逻辑关系和持续时间,以及项目完成所需的最短时间路径。
这有助于项目团队进行进度管理和资源分配,及时发现和解决项目进度延误和资源短缺的问题。
除此之外,网络计划图还可以帮助项目团队进行风险管理。
通过分析关键路径上的活动,我们可以确定哪些活动对项目完成时间具有重要影响,从而有针对性地制定风险应对计划,提前应对潜在的风险。
总之,网络计划图是项目管理中一种非常有用的工具,它可以帮助项目团队清晰地了解项目活动之间的逻辑关系和持续时间,进行进度管理、资源分配和风险管理。
希望通过本文的介绍,您能更好地掌握网络计划图的绘制方法和应用技巧,为项目管理工作提供有力的支持。

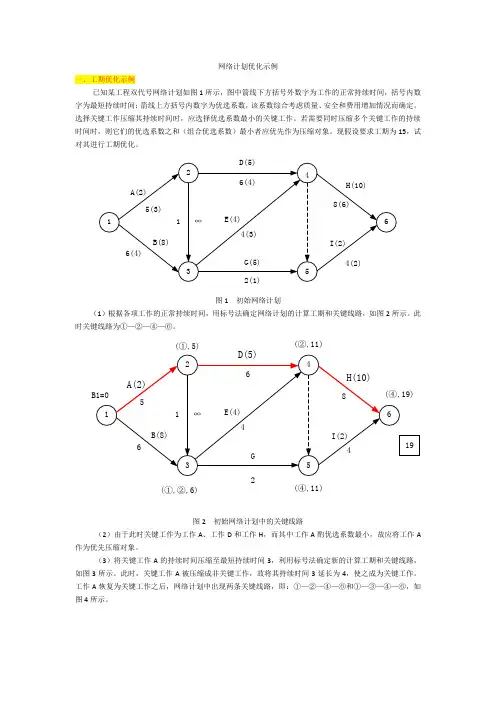
网络计划优化示例一、工期优化示例已知某工程双代号网络计划如图1所示,图中箭线下方括号外数字为工作的正常持续时间,括号内数字为最短持续时间;箭线上方括号内数字为优选系数,该系数综合考虑质量、安全和费用增加情况而确定。
选择关键工作压缩其持续时间时,应选择优选系数最小的关键工作。
若需要同时压缩多个关键工作的持续时间时,则它们的优选系数之和(组合优选系数)最小者应优先作为压缩对象。
现假设要求工期为15,试对其进行工期优化。
图1 初始网络计划(1)根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图2所示。
此时关键线路为①—②—④—⑥。
(①,5)(②,11)(①,②,6)(④,11)图2 初始网络计划中的关键线路(2)由于此时关键工作为工作A、工作D和工作H,而其中工作A酌优选系数最小,故应将工作A 作为优先压缩对象。
(3)将关键工作A的持续时间压缩至最短持续时间3,利用标号法确定新的计算工期和关键线路,如图3所示。
此时,关键工作A被压缩成非关键工作,故将其持续时间3延长为4,使之成为关键工作。
工作A恢复为关键工作之后,网络计划中出现两条关键线路,即:①—②—④—⑥和①—③—④—⑥,如图4所示。
(①,6)(④,10)图3 工作A压缩至最短时间时的关键线路(①,4)(②,③,10)(①,6)(④,10)图4 第一次压缩后的网络计划(4)由于此时计算工期为18,仍大于要求工期,故需继续压缩。
需要缩短的时间:△T=18 -15 = 3。
在图5所示网络计划中,有以下五个压缩方案:①同时压缩工作A和工作B,组合优选系数为:2+8=10;②同时压缩工作A和工作E,组合优选系数为:2+4=6;③同时压缩工作B和工作D,组合优选系数为:8+5=13;④同时压缩工作D和工作E,组合优选系数为:5+4=9;⑤压缩工作H,优选系数为10。
在上述压缩方案中,由于工作A和工作E的组合优选系数最小,故应选择同时压缩工作A和工作E 的方案。
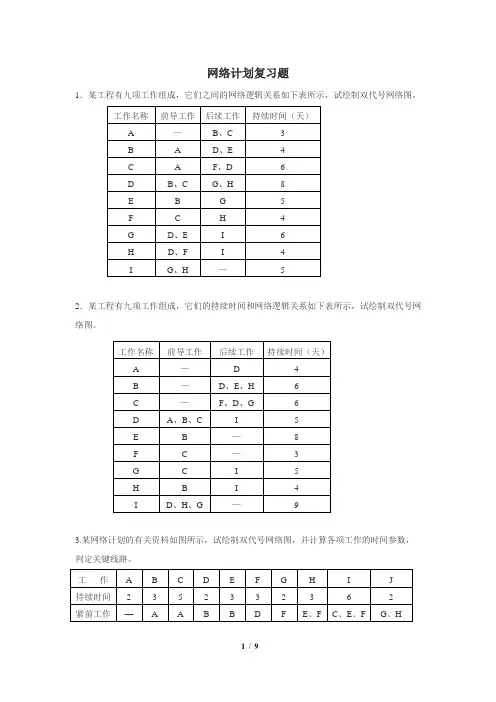
网络计划复习题1.某工程有九项工作组成,它们之间的网络逻辑关系如下表所示,试绘制双代号网络图。
2.某工程有九项工作组成,它们的持续时间和网络逻辑关系如下表所示,试绘制双代号网络图。
3.某网络计划的有关资料如图所示,试绘制双代号网络图,并计算各项工作的时间参数,判定关键线路。
4.某工程由十项工作组成,各项工作之间的相互制约、相互依赖的关系如下所述:A、B 均为第一个开始的工作,G开始前,D、P必须结束,E、F结束后,C、D才能开始;F、Q 开始前,A应该结束;C、D、P、Q结束后,H才能开始;E、P开始前,A、B必须结束;G、H均为最后一个结束的工作。
上述工作持续时间如下表所示:5.某三跨车间地面工程分为A、B、C三个施工段,其施工过程及持续时间如下表。
要求:(1)绘制双代号网络图;(2)指出关键线路和工期。
6. 已知工作明细表如下表所示,试绘制双代号网络图并计算各项工作的时间参数(按工作计算法用六时标注,假定计划工期与计算工期相等)并确定关键线路和总工期。
7.8.某项工程由七项工作组成,其相互关系如下表所示,试绘制单代号网络图并计算各网络时间参数9.某项目相关资料如下表:若公司能在18周内完成项目,将会得到一笔10000元的奖金,但若项目托期到22周以上,就要付出5000元的罚款。
若公司可以选择投标或不投标该项目,而且这个项目只是一个收支平衡的一般项目,应该如何决策?10.某项目相关资料如下表:试计算项目到17周、24周完成的概率,并计算到多少周完成才能达到90%的完成概率?11.一个项目的最早期望结束时间是138天,它的要求完工时间是130天,若标准差σ=6天,求在要求完工时间之前完成项目的概率:12. 根据下表提供的数据资料:要求:(1)按正常条件绘制双代号网络图:(2)计算工序最早开工、最早结束、最迟开工、最迟结束时间、总时差和自由时差并标在图上:(3)求出正常条件下的工期及总成本:(4)已知工期每压缩一周,间接费用节省600元,求最低成本的最短工。


5.3单代号网络计划时间参数计算1.单代号网络计划时间参数的标注形式【示例9】把下图双代号网络图绘制成双代号时标网络图。
复习思考5.1关键工作的判断方法?5.2双代号网络计划与单代号网络计划的区别?5.3关键线路的判断方法?5.4单位(土建)工程网络计划的编制步骤?5.5时差有几种?它们各有什么作用?5.6双代号网络图中,工作时间参数有哪些?在网络图中的表示方法?5.7关键线路的性质有哪些?选择题:CAADC CBCBA BAABC CDA 判断题∨∨∨××∨×选择题1.双代号网络图的三要素是指()。
A.节点、箭杆、工作作业时间B.紧前工作、紧后工作、关键线路C.工作、节点、线路D.工期、关键线路、非关键线路2.利用工作的自由时差,其结果是()。
A.不会影响紧后工作,也不会影响工期B.不会影响紧后工作,但会影响工期C.会影响紧后工作,但不会影响工期D.会影响紧后工作和工期3.下列()说法是错误的。
A.总时差为零的工作是关键工作B.由关键工作组成的线路是关键线路C.总时差为零,自由时差一定为零D.自由时差是局部时差,总时差是线路性时差4.下列()说法是错误的。
A.任何工程都有规定工期、计划工期和计算工期B.计划工期可以小于规定工期C.计划工期可以等于规定工期D.计划工期有时可等于计算工期5.(),会出现虚箭线。
A.当只有相同的紧后工作时B.当只有不相同的紧后工作时C.既有相同,又有不相同的紧后工作时D.不受约束的任何情况6.网络计划的缺点是()。
A.不能反映工作问题的逻辑B.不能反映出关键工作C.计算资源消耗量不便D.不能实现电算化7.某项工作有两项紧后工作C、D,最迟完成时间:C=20天,D=15天,工作持续时间:C=7天,D=12天,则本工作的最迟完成时间是()。
A. 13天B. 3天C. 8天D. 15天8.双代号网络图中的虚工作()。
A.即消耗时间,又消耗资源B.只消耗时间,不消耗资源C.即不消耗时间,又不消资源D.不消髦时间,又消耗资源9.下列有关虚工序的错误说法是()。

节点的相关计算1.结点最早开始时间①当进入结点 J 的箭线只有一条时:ET( j) =ET(i)+t(i,j)②当进入结点 J 的箭线有多条时:ET( j) =max{ET(i k) +t(i k,j)}①若节点 i 的后面只有一条箭线时:j)-t(i,j)LT(i)=LT(②若节点 i 的后面有多条箭线时:LT(i=min{ LT( j k)-t(i,j k)})3.节点时差:S(i)=LT(i)-ET (i )=最迟发生-最早发生作业的相关计算1.作业最早开始时间ES(i,j)=ET(i)或ES(i,j)=max{ES(h,i)+t(h,i)}2.作业最早结束时间EF(i,j)=ES (i,j)+t(i,j)LF(i,j)=LT(j)1. 作业最迟开始时间LS(i,j)=LF (I,j)- t(i,j) =LT(j)- t(i,j )5. 作业时差1) 作业总时差:不影响总工期的前提下,可以利用的机动时间ST(i, j)=LS(i, j)-ES(i, j) =最迟开始-最早开始=LF(i, j)-EF(i, j) =最迟结束-最早完成=LT( j)-ET(i)- t(i, j)1) 作业单时差:不影响下一个作业的机动时间。
S(i, j)=ES(j, k)-EF(i, j)=ES(j, k)-ES(i, j)-t (i, j)=ET(j)-ET(i)-t (i, j)⏹关键作业:总时差为零的作业称为关键作业。
⏹关键路线:把所有关键作业连接起来,所得到的从始点到终点的路线。
⏹路线时差=关键路线长度 -该路线长度。

时限网络计划计算例题英文回答:To calculate the time-limited network plan, we need to consider several factors such as the project tasks, their dependencies, and the estimated durations for each task. The critical path method (CPM) is commonly used to determine the project schedule and identify the critical path.First, we need to identify all the tasks involved in the project. Let's say we are planning a construction project to build a house. The tasks may include obtaining permits, clearing the site, pouring the foundation, framing the structure, installing electrical and plumbing systems, and finishing the interior and exterior.Next, we need to determine the dependencies between these tasks. Some tasks can only start after others have been completed, while some can be done concurrently. Forexample, pouring the foundation cannot start until the site has been cleared, and the framing cannot start until the foundation is in place.Once we have identified the tasks and their dependencies, we can estimate the duration for each task. This can be based on historical data, expert opinions, or previous similar projects. Let's say pouring the foundation takes 2 weeks, framing takes 4 weeks, and so on.Now, we can create a network diagram to visualize the project tasks and their dependencies. This diagram helps us identify the critical path, which is the longest path through the project. The critical path determines the minimum time required to complete the project.To calculate the project duration, we need to determine the early start and finish times for each task. The early start time is the earliest possible time a task can start, considering its dependencies and the durations of preceding tasks. The early finish time is the earliest possible time a task can be completed.We also need to calculate the late start and finish times for each task. The late start time is the latest possible time a task can start without delaying the project, and the late finish time is the latest possible time a task can be completed without delaying the project.By calculating the early and late start and finishtimes for each task, we can determine the total project duration and identify the critical path. The critical path consists of the tasks with no slack or float, meaning any delay in these tasks will delay the entire project.For example, let's say in our construction project, pouring the foundation, framing, and finishing the interior are on the critical path. If pouring the foundation takes longer than estimated, it will delay the framing and finishing tasks, and consequently, the project completion date.In summary, to calculate the time-limited network plan, we need to identify the tasks, determine their dependencies,estimate their durations, create a network diagram, and calculate the early and late start and finish times. The critical path method helps us identify the critical path and determine the minimum project duration.中文回答:要计算时限网络计划,我们需要考虑几个因素,如项目任务、任务之间的依赖关系以及每个任务的预计持续时间。
网络计划复习题答案一、单项选择题1. 在网络计划中,关键路径是指()。
A. 总时差为零的路径B. 总时差大于零的路径C. 总时差小于零的路径D. 总时差等于零的路径答案:A2. 网络计划中,自由时差是指()。
A. 活动最早开始时间与最晚开始时间之差B. 活动最晚开始时间与最早开始时间之差C. 活动最早完成时间与最晚完成时间之差D. 活动最晚完成时间与最早完成时间之差答案:B3. 网络计划中,总时差是指()。
A. 活动最早开始时间与最晚开始时间之差B. 项目最早完成时间与最晚完成时间之差C. 项目最晚完成时间与最早完成时间之差D. 活动最晚完成时间与最早完成时间之差答案:B二、多项选择题1. 以下哪些因素会影响网络计划的制定()。
A. 资源的可用性B. 项目目标C. 项目范围D. 项目风险答案:ABCD2. 网络计划中的关键活动具有哪些特点()。
A. 总时差为零B. 自由时差为零C. 任何延误都会导致项目延期D. 可以随意调整时间答案:ABC三、判断题1. 网络计划中的松弛时间是指活动可以延迟的时间,而不会影响整个项目的完成时间。
()答案:错误2. 网络计划中的活动可以随意调整,只要不改变关键路径上的活动即可。
()答案:错误四、简答题1. 描述网络计划中的关键路径法(CPM)的基本原理。
答案:关键路径法(CPM)是一种项目管理工具,用于确定项目中的关键任务序列。
它通过识别项目中最长的任务序列(即关键路径)来帮助项目经理优化资源分配和时间安排。
关键路径上的任何延迟都会导致整个项目的延期,因此,关键路径上的活动需要特别关注和管理。
2. 网络计划中如何计算活动的最早开始时间(ES)和最晚开始时间(LS)?答案:最早开始时间(ES)是指在不推迟任何后续活动的情况下,活动可以开始的最早时间。
最晚开始时间(LS)是指在不影响项目完成日期的情况下,活动可以开始的最晚时间。
ES和LS的计算通常基于网络计划中的逻辑关系和依赖性,以及活动的持续时间。
网络计划图管理学例题**English:**In the realm of project management, the Network Plan Diagram is a pivotal tool for visualizing and organizing the sequence of tasks.A case in point is the construction of a new office building.The project involves numerous tasks such as design, procurement, and construction, each with its dependencies and constraints.A network plan diagram would illustrate these interdependencies, allowing the project manager to identify critical paths and allocate resources effectively.For instance, the design phase cannot commence until the site is prepared.Consequently, the network diagram would show design as a successor to the site preparation task.Similarly, the procurement of materials depends on the completion of the design phase.This interconnected web of tasks is what a network plan diagram brings to light, aiding in the optimization of project timelines and resource utilization.**中文:**在项目管理领域,网络计划图是一个关键的工具,用于可视化和组织任务序列。