离散数学 欧拉图与哈密尔顿图
- 格式:ppt
- 大小:2.81 MB
- 文档页数:7









欧拉图和哈密顿图是离散数学中的两个重要的图论概念。
它们分别研究了图中的路径问题,对于解决一些实际问题具有很大的应用价值。
欧拉图是指一个无向图中存在一条路径,经过图中的每条边一次且仅一次,这条路径称为欧拉路径。
如果这个路径的起点和终点重合,则称为欧拉回路。
而对于有向图,存在一条路径,使得经过每一个有向边恰好一次,称为欧拉有向路径,如果该路径起点和终点相同,则称为欧拉有向回路。
1722年,瑞士数学家欧拉首次提出了这个概念,并证明了一系列欧拉图的性质。
欧拉图的性质是其路径的存在性。
既然有了这个概念,那如何判断一个图是不是欧拉图就是一个非常重要的问题。
根据欧拉图的定义,我们可以发现,图中的每个节点的度数都应该是偶数,否则该节点无法成为路径中的中间节点。
因此,一个图是欧拉图的充分必要条件是该图中每个节点的度数都是偶数。
哈密顿图是指一个图中存在一条路径,经过图中的每个顶点一次且仅一次,这条路径称为哈密顿路径。
如果这个路径的起点和终点重合,则称为哈密顿回路。
哈密顿图的概念由19世纪初英国数学家哈密顿引入,其研究对象是关于骑士巡游问题。
与欧拉图不同的是,哈密顿路径并没有一个十分明显的判定条件。
唯一已知的是某些图是哈密顿图,比如完全图和圈图。
至于一般的图是否存在哈密顿路径,目前尚无通用的判定方法。
这也是全世界许多数学家所面临的一个著名且具有挑战性的开放问题,被命名为“哈密顿路径问题”。
欧拉图和哈密顿图在实际问题中具有广泛的应用。
欧拉图的应用包括电子电路和网络的设计,路线规划等。
而哈密顿图的应用更多地涉及路径的优化问题,比如旅行商问题。
在实际应用中,我们常常需要通过对欧拉图和哈密顿图的研究,来寻找最优解或者设计最佳路径。
总的来说,离散数学中的欧拉图和哈密顿图是两个重要的图论概念,它们研究的是图中的路径问题。
欧拉图的判定条件相对明确,而哈密顿图的判定则是一个尚未完全解答的开放问题。
这两个概念在实际中具有广泛的应用,对于解决一些路径优化问题具有重要的参考价值。
第十五章欧拉图与哈密顿图15.1 欧拉图 (2)一、欧拉通路、欧拉回路、欧拉图、半欧拉图的定义 (3)二、判别定理 (4)三、求欧拉图中欧拉回路的算法 (6)1.Fleury算法,能不走桥就不走桥: (6)2.逐步插入回路法 (7)四、中国邮路问题 (8)练习题: (9)15.2哈密顿图 (11)一、哈密顿通路、哈密顿回路、哈密顿图、半哈密顿图的定义 (12)二、哈密顿图与半哈密顿图的一些必要与充分条件 (12)练习题 (18)15.3 带权图与货郎担问题 (24)一、带权图 (24)二、货郎担问题 (24)15.1 欧拉图主要内容:1. 欧拉通路、欧拉回路、欧拉图、半欧拉图的定义。
2. 判别定理。
3. 求欧拉图中欧拉回路的算法。
学习要求:1. 深刻理解欧拉通路与欧拉回路的定义以及它们的区别与联系。
2. 以无向欧拉图为例,进一步理解欧拉图的结构,即,欧拉图是若干个边不重的圈之并。
让我们先从两个例子出发,获得有关图的一些直观认识。
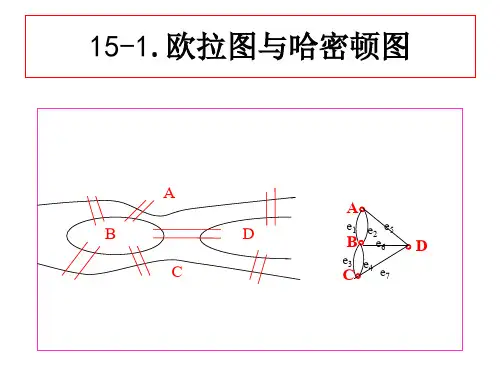
图论的研究起源于哥尼斯堡七桥问题。
哥尼斯堡城位于Pnsel河畔,河中有两个岛,有7座桥与4块陆地彼此相连,如上图所示。
居住于该城的居民想做这样的游戏:从4块陆地的任一块出发,经过每座桥一次且仅一次,最后返回原出发地。
当地的人们进行了许多次尝试,都没有成功。
后来,欧拉给出了问题的解。
首先欧拉将4块陆地表示成4个结点,凡陆地间有桥相连的,便在两点间连一条边,从而可将左图改画为右图如下:这样,哥尼斯堡七桥问题可描述为:能否有从A、B、C、D任一点出发,经过每条边一次且仅一次而返回出发点的回路欧拉证明了这样的回路是不存在的。
他的理由是,从图任一点出发,要回到原出发点,要求与每个点关联的边的数目为偶数,才能保证从一条边进入某点再从另一条边出去,一进一出才能回到原出发点。
而图中的顶点A、B、C和D均有奇数条边与其相关联,显然这样的回路是不存在的。
另一个例子是20世纪40年代的一个数学游戏。