- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
续例 多米诺骨牌问题
d(v i ) 8
viVG
∴能构成回路,能够连成首尾圈。//
[定理] 连通图G,若G中仅有0或2个奇 度数点G有欧拉通路。
<证>
0个奇度数,显然欧拉回路 2个奇度数,u,v,分情况: 1)u,v相邻,删(u,v)余图G’为欧拉图, 从u开始在G’中走欧拉回路,回到u,再 走(u,v)——得到欧拉通路 2) u,v不相邻,向着v方向,取(u,u1)删 (u,u1),以u1为始,重复过程,直至删
c
英
意
e
解二
a:说英语; b:说英语或西班牙语; c;说英语,意大利 语和俄语; d:说日语和西班牙语 e:说德语和意大利语; f:说法语、日语和俄语; g:说法语和德语.
a
英
b
德
g
西
d
法
日
f
如果题目改为:试问这7个人应如何安排座位, 才能使每个人都能与 他身边的人交谈? 解:用结点表示人,用边表示连接的两个人能说讲一种语言,够造 出哈密顿图如右上图所示。
货郎担/旅行推销员(TSP)问题:
在一个赋权的完全图中,找出一个具有最小权 的H_回路,也即回路边的权之和最小 对该赋权图上的边,满足三角不等式(距离不 等式) W(a,b) W(a,c) + W(c,b)
数学模型
构造无向带权图G, VG中的元素对应于每个城市, EG中每 个元素对应于城市之间的道路,道路长度用相应边的权表示。 则问题的解对应于G中包含所有边的权最小的哈密尔顿回路。 G是带权完全图,总共有n!/2条哈密尔顿回路。因此,问题 是如何从这n!/2条中找出最短的一条 eg:含20个顶点的完全图中不同的哈密尔顿回路有约6000万 亿条-(1.216451017)/2,若机械地检查,每秒处理10万条,需 2万年
判断H-图
•
•
任何一个H_图都可以看成是一个基本回路,再 加上其他若干条边
H_图的充分条件和必要条件均有,但尚无充要 条件
H_图的必要条件
G是H_图,则对VG的任意非空真子集S (S, SV,均有 W(G-S)|S| 其中W(G)是G的分支数
必要条件的应用
[证]
设C是G的H_回路
中国邮递员问题-模型
数学模型:
构造无向权图G,以道路为边,路长为权 问题的解——G中包含所有边的回路权最小,称为 最优回路(未必是简单回路)。 当G是欧拉图,则最优回路即欧拉回路。 若G不是欧拉图,则通过加边来消除G中的奇度顶点, 要求使加边得到的欧拉图G'中重复边的权和最小。
周游世界的游戏
3) 1):
Z1是划分中的一个基回,若{Z1}=E,则Z1就 欧拉回路,G是欧拉图 否则,存在另一回路Z2与Z1有公共点v 构造简单回路,从v经Z1回到v,再经Z2回到v
将Z1UZ2看作Z1,再重复 上述过程,得到穷尽EG 的简单回路。 ∴G—欧拉图。//
提示
全部是偶度点的连通图中的回路 若干小回路串成欧拉回路
则W(G-S)=5 |S|=3
必要条件的局限性 ——只能判定一个图不是哈密尔顿图
下图(Petersen图)满足上述必要条件。 Petersen图不是H_图。
H-通路/半哈密尔顿图
充分条件
[定理]简单G有n(n 2)个节点,若G中任二点度数 和大于等于n-1,则G有H-通路 例.有H_通路,无H_回路
货郎担问题的近似算法
1)由任一点v0开始,找一条与之相关联的权最小的边 (V0 ,V1 ),形成初始回路v0 v1
2)设v0 v1 vi 已选定,从V— {v0 v1 vi}中找一点 vi+1 与 vi 距离最近
3)重复2)直到所有节点都在通路中 4)连接始点与终点
不一定是最佳解
∴ Kn是H-图
只要图中边足够多,G易为H_图 只要图中成对节点度数足够大,G易为H_图
间接充要条件
[引理] 设 G中u,v不相邻,且 d(u)+d(v) n,则 G+{(u,v)}是H_图的充要条件是G 是H_图
<定义>闭合图C(G):
在G中反复增添结点度数和|VG|的不相邻的 节点对上的边,直至不能再添,得到的图为闭 合图C(G)
欧拉图和哈密尔顿图
信号处理中的数学方法 第2-4讲
一.欧拉回路:一般不限于简单图,一般指无向
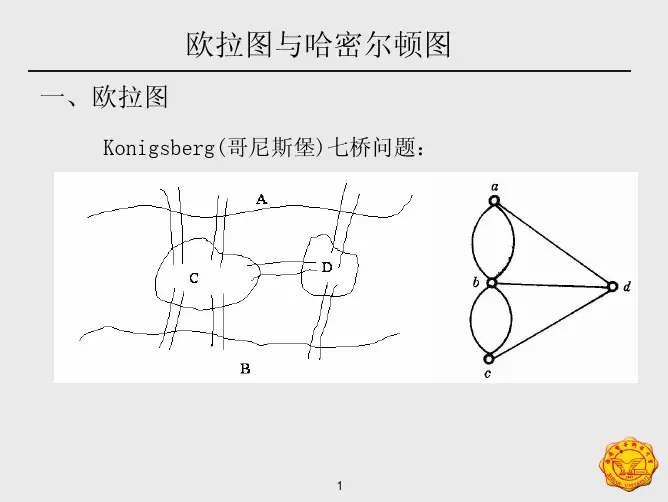
图 Eg. 哥尼斯堡七桥问题
原问题:“右边的图中是否存在包含每条边一次且恰好 一次的回路?” 原问题等价于:欧拉图
A D C B A D
C
B
<定义>欧拉回路,欧拉通路
图G的一个回路/通路,它经过G中每条边恰 好一次,则回路/通路称为欧拉回路/通路。 定义:如果图G中含欧拉回路,则图G称为 欧拉图。
图G的闭合图是唯一的
例
加成了完全图, 故是H_图
“如果只在满足 d(u)+d(v) n 的 u,v 之间加边——构造 闭合图,图的哈密尔顿性质不会改变”
棋盘上的哈密尔顿回路问题
在44或55的缩小了的国际象棋棋盘上,马 (Knight)不可能从某一格开始,跳过每个格 子一次,并返回起点。
G连通,不妨设G是非平凡图
由2)每个结点度数至少为2,所以G中含一基回 Z1,Z1的度数为偶度数,删去Z1的边得到G’, 原G为偶度数,删去G’的每个点仍为偶度数 除孤立点外其余点至少为2度,即余连通点所图 至少2连通
如法炮制,直至余图不含边
{Z1},{Z2 },…..,{Zk }为E的一个划分。 //
提示:
在画欧拉回路时,已经经过的边不能再用;
在走回路中的任何时刻,将已经经过的边删 除,剩下的边必须仍在同一连通分支当中
×
随机欧拉图
<定义>G是欧拉图,vVG,从v开始,每一步从当前 点所关联边中随机选边,均可构造欧拉回路,则G称为 以v为始点的随机欧拉图。
注,若G是以v为始点的随机欧拉 图,则任何一个以v为始点的不包含G 中所有边的回路都应该能扩充成欧拉 回路。反之,若G不是以v为始点的随 机欧拉图,则一定存在已经包含了v 所关联的所有边,却未包含G中所有 边的简单回路。
这样,该问题转化为G有无欧拉回路的问题
[定理]对连通图,下列命题等价
1)G是欧拉图
2)G的每个结点为偶度数 3)G的边集能划分成为基本回路,即
eg.
边集C1 ,C 2 ,,C k 不重叠之基本回路,且 UC i E G
i=1
k
[证]
1)2)3) 1)
1) 2):
定义:如果图G中仅有欧拉通路,但没有欧 拉回路,则图G称为半欧拉图。
例 “一笔划”问题——G中有欧拉 通路
?
实例
上图中,(1) ,(4) 为欧拉图
例 多米诺骨牌,28块
能否排成一圈使两两相邻的半边的点数相同,问 是否可能?
牌数
C
2 7
7 28 种
将0-6看作7个结点,任2点的边看作一块骨牌
D
I L O G M J
D
K
K H N H
F
参观区域实景 设E为起始点
图G
E,N,M,O,L,K,I,L,M,J,N,D,C,J,B,I,A,K,H,G,O,F,E
<欧拉回路-Fleury算法 >
1) 任取一点v0,置w0=v0
2) 设简单回路wi= v0e1v1e2……eivi 已选定, 则从EG−{e1e2……ei}中选ei+1
则分别用边 vivi+1 和 vjvj+1 替代 vivj 和 vi+1vj+1。
a
14
从a出发的“较好的”回路长度:40
10 12
9 a 7 d 6 c 8 e 5 b 14 10 a
b
7 13 5
9
c
6
经改进的回路,长 度:37 e
e
9
d
11
a
7
d 6
c
e
5
b
a
10
随机欧拉图的判定
[定理] 欧拉图G是以v为始点的随机欧拉图当且仅 当G中任一回路均包含v。 [推论] 欧拉图G是以任一顶点为始点的随机欧拉图 当且仅当G本身是一个基本回路)
中国邮递员问题:
问题:邮递员从邮局出发,走过辖区内每条 街道至少一次,如何选择最短路线? 1)每街一次/至少一次 2)环游最短
(ui,v)后得到欧拉回路,连上所删除的边,得 到——得到欧拉通路。//
续例
.―一笔划”问题
G连通,从一个奇度点开始画,图只有0或2 个奇度点,则G可一笔画。//
[定理] 对有向图,G有欧拉回路每一结
点入度等于出度。
安排国展中心参观路线
A A B C I B J L O E F E G M N C
例
a
从a出发的“较好的”回路 ,
10 12
14
b
7 13 11
a
7
d
6
c
8
e
5
b
14
a
9
c
5
6
8
长度:40
d e
e
算法精度下限
设算法所得的回路长度为d, d0 是最小H_
回路的长度,G有n点,则
d / d0 ½ [ln(n)+1]+ ½
改进:
如果在已有回路中,W(vi,vj)+ W(vi+1,vj+1)< W(vi,vi+1)+ W(vj,vj+1),
1859 哈密尔顿 “周游世界”游戏: 20个城市,每个城市恰游一次,回到出发地