当前位置：文档之家 › 欧拉图和汉密尔顿图

欧拉图和汉密尔顿图

  • 格式：ppt
  • 大小：1.75 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

第15章 欧拉图与哈密顿图

第15章 欧拉图与哈密顿图

e5
v3
v2 e1 v1
e2
e3
e4
v4
e5
v3 e3 e4 v4
v2 v1 v5
e2 e3
e1 e5
v3 e4 v4 v6
v1
e6 v5 e7 e8 v6 e2 e3
e8 v5
e8 v6 v5 e2 v6
e7
G
v2 e1 v1 v5 v6 v3 e4 v4 v5 v2
G1
e2 v3 e4 v2 e1 v1 v5 e1
定理15.7
定理15.7 设G是n阶无向简单图，若对于G中任意不相邻的顶 点vi,vj，均有 d(vi)+d(vj)≥n-1 (15.1) 则G中存在哈密顿通路。 证明 首先证明G是连通图。 否则G至少有两个连通分支， 设G1,G2是阶数为n1,n2的两个连通分支， 设v1∈V(G1)，v2∈V(G2)，因为G是简单图，所以 dG(v1)+dG(v2)＝dG1(v1)+dG2(v2)≤n1-1+n2-1≤n-2 这与(15.1)矛盾，所以G必为连通图。
例15.3的说明
哈密顿通路是经过图中所有顶点的一条初级通路。 哈密顿回路是经过图中所有顶点的初级回路。 对于二部图还能得出下面结论： 一般情况下，设二部图G＝<V1,V2,E>，|V1|≤|V2|，且 |V1|≥2，|V2|≥2，由定理15.6及其推论可以得出下面结 论： (1) 若G是哈密顿图，则|V1|＝|V2|。 (2) 若G是半哈密顿图，则|V2|＝|V1|+1。 (3) 若|V2|≥|V1|+2，则G不是哈密顿图，也不是半哈密 顿图。
§15.2 哈密顿图
设图为G2，则G2＝<V1,V2,E>，其中 V1＝{a,g,h,i,c}，V2＝{b,e,f,j,k,d}， 易知，p(G2-V1)＝|V2|＝6>|V1|＝5， 由定理15.6可知，G2不是哈密顿图， 但G2是半哈密顿图。 baegjckhfid为G2中一条哈密顿通路。 设图为G3。G3＝<V1,V2,E>，其中 V1＝{a,c,g,h,e}，V2＝{b,d,i,j,f}， G3中存在哈密顿回路。 如 abcdgihjefa， 所以G3是哈密顿图。

7-4欧拉图与汉密尔顿图

7-4欧拉图与汉密尔顿图

证明（略）。
定理4. 5 设G是具有n个结点的简单图，如果G中每一对结点度数之和大 于等于n，则在G中存在一条汉密尔顿回路。 证明（略）。
（3）充要条件
定义4. 4 设给定图G=<V，E>有n个结点，若将图G中度数之和至少是n的 非邻接结点连接起来得图G’，对图G’重复上述步骤，直到不再有这样的结 点对存在为止，所得到的图，称为原图G的闭包，记作C(G)。 定理4. 6 当且仅当一个简单图的闭包是汉密尔顿图时，这个简单图是汉密尔顿图。 证明:略。
证明: 设C是G的一条汉密尔顿回路，则对于V的任何一个非空子集S在C中 删去S中任一结点a1，则C－a1是连通的非回路，若再删去S中另一结点a2， 则W(C- a1- a2)≤ 2，由归纳法可得： W(C-S)≤ |S| 同时C-S是G-S的一个生成子图（包含G的每个结点的子图），因而 W(G-S)≤ W（C-S） 所以 W(G-S)≤ |S|。 证毕。
证明：
推论 无向图G具有一条欧拉回路，当且仅当G是连通的，并 且所有结点度数全为偶数。
定理4. 1 证明
必要性 设G具有欧拉路，即有点边序列v0e1v1e2…eiviei+1…ekvk，其中
结点可能重复出现，但边不重复，因为欧拉路经过图G的所有结点， 故图G必是连通的。 对任意一个不是端点的结点vi，在欧拉路中每当vi出现一次，必 关联两边，故vi虽可重复出现，但deg(vi)必是偶数。对于端点，若 v0=vk，则d(v0)为偶数，即G中无奇数度结点；若端点v0与vk不同， 则d(v0)为奇数，d(vk)为奇数，G中就有两个奇数结点。 充分性 若图G连通,有零个或两个奇数结点,我们构造一条欧拉路如下：
二、汉密尔顿图
1、正十二面体问题 2、汉密尔顿图的定义 3、汉密尔顿图的判别条件

欧拉图和哈密尔顿图

欧拉图和哈密尔顿图

例 “一笔划”问题——G中有欧拉 通路
？
实例
上图中，(1) ,(4) 为欧拉图
中国邮递员问题-模型
数学模型：
构造无向权图G，以道路为边，路长为权 问题的解 ——G 中包含所有边的回路权最小，称为 最优回路(未必是简单回路)。 当G是欧拉图，则最优回路即欧拉回路。
周游世界的游戏
1859 哈密尔顿 “周游世界”游戏： 20个城市，每个城市恰游一次，回到出发地
例
a
10 12 9
从a出发的“较好的”回路 ， a
7
14Biblioteka b7 13 11d
6
c
8
e
5
b
14
a
c
5
6
8
长度：40
e
e
d
算法精度下限
设算法所得的回路长度为d， d0 是最小H_
回路的长度，G有n点，则

d / d0 ½ [ln(n)+1]+ ½
改进：
如果在已有回路中，W(vi,vj)+ W(vi+1,vj+1)< W(vi,vi+1)+ W(vj,vj+1),
货郎担/旅行推销员(TSP)问题：
在一个赋权的完全图中，找出一个具有最小权 的H_回路，也即回路边的权之和最小 对该赋权图上的边，满足三角不等式（距离不 等式） W(a,b) W(a,c) + W(c,b)
数学模型
构造无向带权图G， VG中的元素对应于每个城市， EG中每 个元素对应于城市之间的道路，道路长度用相应边的权表示。 则问题的解对应于G中包含所有边的权最小的哈密尔顿回路。 G是带权完全图，总共有n!/2条哈密尔顿回路。因此，问题 是如何从这n!/2条中找出最短的一条 eg：含20个顶点的完全图中不同的哈密尔顿回路有约6000万 亿条-(1.216451017)/2，若机械地检查，每秒处理10万条，需 2万年

概率论-第二十一讲--欧拉图与哈密尔顿图(略)

概率论-第二十一讲--欧拉图与哈密尔顿图(略)
16
二、哈密尔顿图
例5. 证明下图中没有汉密尔顿路径。 图中，3个顶点标记为A，5个顶点 A 标记为B，相差2个，不可能存在 一条汉密尔顿路径。 B B 如果在标记过程中，遇到相邻结 点出现相同标记时，如果有一个 结点的度数为2，可在此对应边上 A A 增加一个结点，并标上相异标 A 记。 B B B B B
11
二、哈密尔顿图
定理3：若无向图G=<V,E>是哈密尔顿图， V1是V的任意非空 真子集，则 ω(G- V1)≤| V1 |。 证明：设C是G的一条哈密尔顿回路，对于V的每个非空真子集 V1有：ω(C-V1) ≤|V1|
ω(C- V1)是C删去V1中所有顶点及关联的边后所得图
的连通分支数。 又因为C - V1是G - V1的生成子图，故有
13
二、哈密尔顿图
定义3：若无向图G＝<V,E>的顶点集合V可以划分成两个子集X 和Y，使G中的每一条边e的一个端点在X中，另一个端点 在Y中，则称G为二部图或偶图。二部图可记为 G＝<X,E,Y>，X和Y称为互补结点子集。 二部图不会有自回路。
14
二、哈密尔顿图
定理4：设二部图G=<X, E, Y>，设|X|=m，|Y|=n。若m≠n，则G 必不是汉密尔顿图。 证明：方法1. 用汉密尔顿图的性质证明。 因为|X|≠|Y|，不妨设|X|<|Y|。 显然有ω(G-X)=|Y|>|X|， 这与汉密尔顿图的必要条件ω(G-X)≤|X|矛盾。 因此G必不是汉密尔顿图。
定理2：一个有向连通图具有欧拉路径，当且仅当它 的每个顶点的引入次数等于引出次数，可能 有两个顶点除外，其中一个的引入次数比它 的引出次数大1，另一个的引入次数比它的 引出次数小1。 推论： 一个有向连通图具有欧拉回路，当且仅当它 的每个顶点的引入次数等于引出次数。

欧拉图与哈密顿图

欧拉图与哈密顿图

Fleury算法示例
例15.2
下图是给定的欧拉图G。某人用Fleury算法求G中的欧拉回路时 ，走了简单回路v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2之后(观看他的 错误走法)，无法行遍了，试分析在哪步他犯了错误? 解答 此人行遍v8时犯了能不走桥就不走桥 的错误，因而他没行遍出欧拉回路。 当他走到v8时，G-{e2,e3,e14,e10,e1,e8} 为下图所示。 此时e9为该图中的桥，而e7,e11均不是桥， 他不应该走e9，而应该走e7或e11，他没 有走，所以犯了错误。注意，此人在行 遍中，在v3遇到过桥e3，v1处遇到过桥 e8，但当时除桥外他无别的边可走，所 以当时均走了桥，这是不会犯错误的。
≤ p(G -V1)+1 ≤ |V1|+1
例15.3
例15.3 在下图中给出的三个图都是二部图。它们中的哪些是 哈密顿图？哪些是半哈密顿图？为什么？ 易知互补顶点子集 V1＝{a,f} V2＝{b,c,d,e} 设此二部图为G1，则G1＝<V1,V2,E>。 p(G1-V1)＝4>|V1|＝2， 由定理15.6及其推论可知，G1不是哈 密顿图，也不是半哈密顿图。
因为Г只有两个端点且不同，因而G中只有两个奇数顶点。
另外，G的连通性是显然的。
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的，且G中恰有两 个奇度顶点。
证明 充分性。设G的两个奇度顶点分别为u0和v0，
对G加新边（u0,v0），得G ＝G∪(u0,v0)， 则G 是连通且无奇度顶点的图， 由定理15.1可知，G 为欧拉图， 因而存在欧拉回路C ，而C＝C -(u0,v0)为G中一条欧拉通路，
哈密顿回路是生成的初级回路。

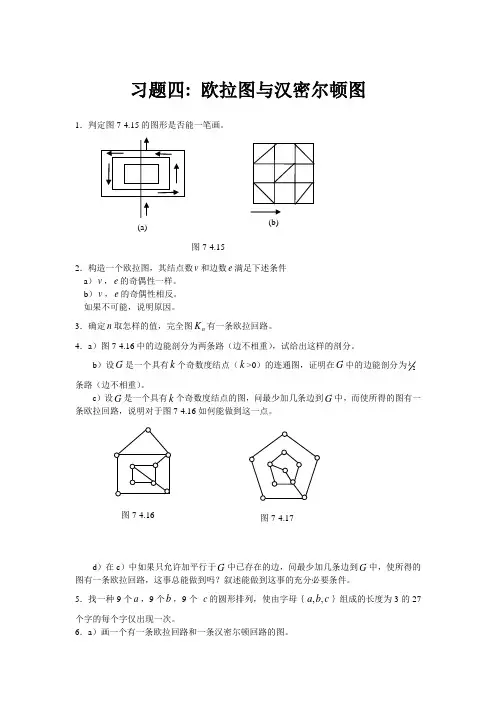
习题四 欧拉图与汉密尔顿图 - 烟台大学计算机与控制工程学院

习题四 欧拉图与汉密尔顿图 - 烟台大学计算机与控制工程学院

习题四: 欧拉图与汉密尔顿图1．判定图7-4.15的图形是否能一笔画。

2．构造一个欧拉图，其结点数v 和边数e 满足下述条件 a ）v ，e 的奇偶性一样。

b ）v ，e 的奇偶性相反。

如果不可能，说明原因。

3．确定n 取怎样的值，完全图n K 有一条欧拉回路。

4．a ）图7-4.16中的边能剖分为两条路（边不相重），试给出这样的剖分。

b ）设G 是一个具有k 个奇数度结点（k >0）的连通图，证明在G 中的边能剖分为2k 条路（边不相重）。

c ）设G 是一个具有k 个奇数度结点的图，问最少加几条边到G 中，而使所得的图有一条欧拉回路，说明对于图7-4.16如何能做到这一点。

d ）在c ）中如果只允许加平行于G 中已存在的边，问最少加几条边到G 中，使所得的图有一条欧拉回路，这事总能做到吗？叙述能做到这事的充分必要条件。

5．找一种9个a ，9个b ，9个 c 的圆形排列，使由字母｛c b a ,,｝组成的长度为3的27个字的每个字仅出现一次。

6．a ）画一个有一条欧拉回路和一条汉密尔顿回路的图。

图7-4.15(a)(b)图7-4.16图7-4.17b ）画一个有一条欧拉回路，但没有一条汉密尔顿回路的图。

c ）画一个没有一条欧拉回路，但有一条汉密尔顿回路的图。

7．判断图7-4.17所示的图中是否有汉密尔顿回路。

8．设G 是一个具有n 个结点的简单无向图，3≥n ，设G 的结点表示n 个人，G 的边表示他们间的友好关系，若两个结点被一条边连结，当且仅当对应的人是朋友。

a ）结点的度数能作怎样的解释。

b ）G 是连通图能作怎样的解释。

c ）假定任意两人合起来认识所留下的n -2个人，证明n 个人能站成一排，使得中间每个人两旁站着自己的朋友，而两端的两个人，他们每个人旁边只站着他的一个朋友。

d ）证明对于n 4≥，c ）中条件保证n 个人能站成一圈，使每一个人的两旁站着自己的朋友。

9．证明如G 具有汉密尔顿路，则对于V 的每一个真子集S 有 1)(+≤-S S G W10．一个简单图是汉密尔顿图的充要条件是其闭包是汉密尔顿图。

第三章 哈密顿图

第三章 哈密顿图
– –
(1) G的每条边在G*至多重复一次；
(2) G的每个(初级)圈在G*重复边权的和不超过该圈 权的一半。

算法过程
–
1．用Dijstra算法求所有奇度顶点对之间的最短路径。 (若G是欧拉图，直接用Fleury算法) 2．以G中所有奇度顶点构造带权完全图G2k, 每边的 权是两端点间最短路径长度。
1
2
20
17
19
18Biblioteka 义： 图G中的一圈，若它通过G中每个顶 点恰好一次，则该圈称为哈密尔顿圈，具 有哈密尔顿圈的图称为哈密尔顿无向图。 完全图必是哈密尔顿图。
从定义可知，一个图的Hamilton圈与
Euler环游是很相似的，差别在于Hamilton
圈是环游G的所有顶点圈（点不重，当然
边也不重），而Euler环游是环游G的所
道的交叉点，街道长度用相应边的权表示。 则问题的解对应于G中包含所有边的权最小 的圈，称为最优圈(注意：未必是简单圈)。 当G是欧拉图，则最优圈即欧拉圈。 若G不是欧拉图，则通过加边来消除G中的 奇度顶点，要求使加边得到的欧拉图G'中重复边
的权和最小。
C是带正权无向连通图G中的最优圈当且仅当对 应的欧拉图G*满足：
边外,,每经过G中顶点xi(包括a和b),都为顶点xi
贡献2度,而C的第一边为a贡献1度,C的最后一条
边为b贡献1度.因此,a和b的度数均为奇数,其余
结点度数均为偶数.
充分性:设连通图G恰有两个奇数度结点,
不妨设为a和b,在图G中添加一条边e={a,b} 得G’,则G’的每个结点的度数均为偶数,因 而G’中存在欧拉圈,故G中必存在欧拉路.
J K
例3 一张纸上画有如下图所示的图，你能否用剪刀 一次连续剪下图中的三个正方形和两个三角形？

《离散数学》 第八章 欧拉图与哈密尔顿图

《离散数学》 第八章 欧拉图与哈密尔顿图

1 10 1
8.1 欧拉图
8.1.4 欧拉图的应用
欧拉图的应用，计算机旋转鼓轮的设计原理。
现在构造一个有向图G，G有8个顶点，每个顶点分别表示 000～111的一个二进制数。设α i∈{0，1}，从顶点α 1α 2α 3 引出两条有向边，其终点分别为α 2α 30和α 2α 31，这两条边 分别为α 1α 2α 30以及α 1α 2α 31，按照此种方法，对于八个 顶点的有向图共有16条边，在这个图的任意一条通路中，其 邻接的边必是α iα jα kα t和α jα kα tα s的形式，即前一条有 向边的后3位与后一条有向边的前3位相同。因为图中的16条 边被记成不同的4位二进制信息，即对应于图中的一条欧拉 回路。
推论 无向连通图中顶点与间存在欧拉通路，当且仅当中 与的度数为奇数，而其他顶点的度数为偶数。
8.1 欧拉图
8.1.2 欧拉图的判定
b
a
d
c
图8.1-2
v1
v2
v1
v3
v4
v5
v6
v2
(a)
图8.1-3
v4
v3 (b)
8.1 欧拉图
8.1.2 欧拉图的判定
定理8.1.3 有向图是欧拉图，当且仅当是强连通的，且 中每个顶点的入度都等于出度。
8.2 哈密尔顿图
8.2.1 哈密尔顿图
在图8.2-2中，（a）、（b）中存在哈密尔顿回路，是哈密 尔顿图，（c）中存在哈密尔顿通路，但不存在哈密尔顿回 路，是半哈密尔顿图，（d）中既无哈密尔顿回路，也无哈 密尔顿通路，不是哈密尔顿图。
（ a）
（ b）
（ c）
（ d）
8.2 哈密尔顿图
8.2.2 哈密尔顿图的判定

欧拉图和哈密而顿图

欧拉图和哈密而顿图
15.1 欧拉图 欧拉(1707-1783)：瑞士著名的数学家。13岁进入 欧拉 ：瑞士著名的数学家。 岁进入 巴塞尔大学， 岁取得哲学硕士学位 岁取得哲学硕士学位。 巴塞尔大学，16岁取得哲学硕士学位。1736年， 年 他证明了欧拉定理， 他证明了欧拉定理，并解决了哥尼斯堡桥的问 从而成为图论的创始人。 题，从而成为图论的创始人。 定义15.1 通过图（无向图或有向图）中每一条边 通过图（无向图或有向图） 定义 一次且仅一次行遍图中所有顶点的通路称为欧 拉通路。通过图（无向图或有向图） 拉通路。通过图（无向图或有向图）中每一条 边一次且仅一次行遍图中所有顶点的回路称为 欧拉回路。具有欧拉回路的图称为欧拉图， 欧拉回路。具有欧拉回路的图称为欧拉图，具 有欧拉通路而无欧拉回路的图称为半欧拉图。 有欧拉通路而无欧拉回路的图称为半欧拉图。
16
15.欧拉图与哈密顿图 欧拉图与哈密顿图
15.2 哈密顿图
到目前为止， 到目前为止，还没有找到哈密尔顿通路存在的充 分必要条件。下面介绍一个必要定理。 分必要条件。下面介绍一个必要定理。 定理15.6：设无向图 Ｇ＝＜Ｖ ， Ｅ＞ 是哈密尔顿 Ｇ＝＜Ｖ， 定理 ： 设无向图Ｇ＝＜Ｖ Ｅ＞是哈密尔顿 图，则对V的每个非空真子集 均成立： 则对 的每个非空真子集S均成立： 的每个非空真子集 均成立 w(G-S) ≤|S| 其中， 中的顶点数， 表示G删去 其中， |S| 是S中的顶点数， w(G-S)表示 删去 中的顶点数 表示 删去S 顶点集后得到的图的连通分图的个数。 顶点集后得到的图的连通分图的个数。
9
15.欧拉图与哈密顿图 欧拉图与哈密顿图
例：用定理解决哥尼斯堡桥的问题
15.1 欧拉图
个结点为奇次数， 有４个结点为奇次数， ∴不存在欧拉回路，也不存在欧拉路径。 不存在欧拉回路，也不存在欧拉路径。 故要从一点出发经过桥一次且仅一次的路径， 故要从一点出发经过桥一次且仅一次的路径 ， 再回到出发点是不可能的。 再回到出发点是不可能的。

欧拉图和汉密尔顿图

欧拉图和汉密尔顿图

生物信息学
在生物信息学中，欧拉图 和汉密尔顿图可以用于表 示和分析基因组、蛋白质 组等生物分子网络。
社会学
在社会学中，欧拉图和汉 密尔顿图可以用于表示和 分析社会关系、社交网络 等方面的问题。
05
总结与展望
对欧拉图和汉密尔顿图的总结
01
欧拉图和汉密尔顿图是 图论中的重要概念，分 别由数学家欧拉和汉密 尔顿提出。
人工智能
汉密尔顿图在人工智能领域也有应用，例如在知识表示和推理中，可以利用汉密尔顿路径 来表示和推理复杂的逻辑关系。
机器学习
汉密尔顿图还可以应用于机器学习中，特别是在图神经网络（GNN）中，可以利用汉密尔顿 路径进行节点间的信息传递和传播。
欧拉图与汉密尔顿图在其他领域的应用
01
02
03
交通运输
欧拉图和汉密尔顿图在交 通运输领域有广泛应用， 例如在路线规划、物流配 送和交通控制等方面。
汉密尔顿图是指一个图中存在一条遍历其所有顶点的路径，且每条边只遍 历一次。
当一个汉密尔顿图的起点和终点是同一点时，该路径就成为欧拉路径，此 时汉密尔顿图也就是欧拉图。
欧拉图与汉密尔顿图的判定问题
欧拉图的判定问题
给定一个图，判断是否存在一条遍历 其所有边且每条边只遍历一次的路径。
汉密尔顿图的判定问题
02
欧拉图是指存在一条或 多条路径能够遍历图的 所有边且每条边只遍历 一次的图。
03
汉密尔顿图是指存在一 条路径能够遍历图的所 有顶点且每条边只遍历 一次的图。
04
欧拉图和汉密尔顿图在 计算机科学、运筹学、 电子工程等领域有广泛 的应用。
对欧拉图和汉密尔顿图未来的研究方向
寻找更高效的算法来判断一个图是否为欧拉图或汉密尔 顿图，以及寻找更多的应用场景。

离散数学15 欧拉图与哈密顿图

离散数学15 欧拉图与哈密顿图
穿过每一道门，通过所有房间？
15.2 哈密顿图
1859年，爱尔兰数学家威廉·哈密尔顿发明 了一个旅游世界的游戏。将一个正十二面体的 20个顶点分别标上世界上大城市的名字，要求 玩游戏的人从某城市出发沿12面体的棱，通过 每个城市恰一次，最后回到出发的那个城市。
哈密尔顿游戏是在左图中如何 找出一个包含全部顶点的圈。
定义（哈密顿通路和哈密顿回路） 经过图（有向图或无向图）每个顶点一次
且仅一次的通路称为哈密顿通路。 经过图每个结点一次且仅一次的回路（初
级回路）称为哈密顿回路。 定义（哈密顿图和半哈密顿图）
存在哈密顿回路的图称为哈密顿图。 存在哈密顿通路但不存在哈密顿回路的图 称为半哈密顿图。 平凡图是哈密顿图。
由两判定定理，立即可知 （4）为欧拉图， （5）、（6）即不是欧拉图，也不是半欧拉图。
例15.2（P296） v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2
◼ Fleury算法
◼ （1）任取v0V(G)，令P0=v0。 ◼ （2）设Pi=v0e1v1e2…..eivi已经行遍，则按下面
判断所示两图是否为欧拉图、半欧拉图？
无向欧拉图与无向半欧拉图的判断方法
定理15.1（无向欧拉图的判定）无向图G是欧拉图当 且仅当G是连通图，且G中没有奇度顶点。
定理15.2（无向半欧拉图的判定）无向图G是半欧拉 图当且仅当G是连通图，且G中恰有两个奇度顶点。
（1）
（2）
（3）
有向欧拉图与有向半欧拉图的判断方法
（1）
（2）
（3）
（4）
（5）
（6）
（1）（2）（3）（4）为哈密顿图 （5）为半哈密顿图 （6）既不是哈密顿图，又不是半哈密顿图。

欧拉图和哈密顿图

欧拉图和哈密顿图

例如，由定理可知，下图 (a)图为欧拉图，本图 既v成圈8 可圈画v6之v以在1并(看vc2)(成v中为3 圈v)清。4 vv晰1将5v起v2(6av见v)87分v，v1解8，将v成1v与42若个v圈3干圈vv42个画vv24边在，v6不(vb4v)8重v中5v2的v)之6，圈v并也4，的(可两v并6看个v7 不是(a)图特有性质，任何欧拉图都有这个性质。
尽管讨论哈密顿通路和哈密顿回路在形式上与欧
拉通路和欧拉回路非常相似，但遗憾的是到目前为止， 仍然没有找到一个合适的条件来作为判断哈密顿通路 或哈密顿回路存在的充要条件。不过，可以给出哈密 顿通路和哈密顿回路存在的充分条件或必要条件。
定理9.2.1设无向图G=<V, 的任意非空子集，则
E>是哈密顿图，V1是V
下面给出一些哈密顿图的充分条件。
定理9.2.2设G=<V, E>是具有n个节点的简单无向图，若
对任意的u, v∈V均有
deg(v) +deg(u) ≥n－1
则G中存在哈密顿通路。
容易看出，定理9.2.2中的条件对图中是否存在哈密顿路 是充分而不必要的。
如图9.2.6所示的六边形G，虽然任意两个节点度数之和 等于4<6-1(n=6)，但G中却显然有哈密顿路（实际上G是哈密 顿图）。
只要数一下图中节点的度数即可。
❖ 9.1.4 欧拉图的应用 一笔画问题 所谓“一笔画问题”就是画一个图形，笔不离纸，每条 边只画一次而不许重复地画完该图。“一笔画问题”本质上 就是一个无向图是否存在欧拉通路（回路）的问题。如果该 图为欧拉图，则能够一笔画完该图，并且笔又回到出发点； 如果该图只存在欧拉通路，则能够一笔画完该图，但笔回不 到出发点；如果该图中不存在欧拉通路，则不能一笔画完该 图。

第13节欧拉图与哈密顿图

第13节欧拉图与哈密顿图
18/25
集合与图论
哈密顿图的充分条件之一
若顶点vir-1,(r=2,3,...,k)与顶点vp相邻， 则G 有哈密顿圈v1v2...vi(r-1)vpvp-1...virv1.
因此vp至少与v1,v2,...,vp-1中的k个顶点不相邻. vp的度数为h，于是h≤p-1-k，从而k+h≤p-1， 因此k与h中至少有一个小于p/2，G 中有一个顶 点的度小于p/2.
集合与图论
欧拉图的判别定理
若G2中还有边，则同样的方式，G2中有圈Z3，如 此等等，最后必得到一个图Gn，Gn中无边. 于是我们得到了G中的n个圈Z1,Z2,...,Zn,，它们是两 两无公共边的，因此，G的每条边在且仅在其中的一个 圈上，于是G的边集被划分为n个圈. 由于G是连通的，所以每个圈Zi至少与其余的某个 圈有公共顶点，从而图G由一些边不重的相互之间有公 6/25 共顶点的圈构成.
19/25
集合与图论
哈密顿图的充分条件之二
定理3 设G是有p(p≥3)个顶点的图，如果 对G的任意一对不相邻的顶点u和v，均有 degu+degv≥p， 则G是一个哈密顿图. 只需证明p(p≥3)个顶点的每个非哈密顿图中至少 有两个不相邻的顶点u和v，有degu+degv≤p-1即可. 刚才的证明中的v1，vp就满足这个性质.
22/25
集合与图论
实 例
例4：某次国际会议8人参加，已知每人至少与其余7 人中的4人有共同语言，问服务员能否将他们安排在 同一张圆桌就座，使得每个人都与两边的人交谈？ 解 做无向图G=<V,E>, 其中 V={v| v为与会者}， E={{u,v} | u,vV且u与v有共同语言，且u v}. 易知G为无向图且vV, deg(v)4，于是，u,vV, 有 deg(u)+deg(v) 8，可知G为哈密顿图. 服务员在G中 找一条哈密顿圈C，按C中相邻关系安排座位即可.

离散数学-几种特殊图

离散数学-几种特殊图

第四讲几种特殊图一、小结本讲主要介绍欧拉图与汉密尔顿图、平面图与着色以及一些相关的概念与结论等。

1．欧拉图的概念给定无孤立结点图G ，若存在一条路经过图G的每条边一次且仅一次，则该路称为欧拉路；若存在一条回路经过图G的每条边一次且仅一次，在该回路称为欧拉回路；具有欧拉回路的图称为欧拉图；具有欧拉路但无欧拉回路的图称为半欧拉图。

规定平凡图为欧拉图。

2．欧拉路与回路存在的充要条件无向图G具有一条欧拉路，当且仅当G是连通的，且有零个或2个奇数度数的结点。

无向图G具有一条欧拉回路，当且仅当G是连通的，并且它的结点度数都是偶数的。

3．汉密尔顿图的概念给定图G ，若存在一条路经过图G的每个结点一次且仅一次，则该路称为汉密尔顿路；若存在一条回路经过图G的每个结点一次且仅一次，则该回路称为汉密尔顿回路；具有汉密尔顿回路的图称为汉密尔顿图；具有汉密尔顿路但无汉密尔顿回路的图称为半汉密尔顿图。

4．汉密尔顿回路存在的必要条件若图G=<V,E>中具有一条汉密尔顿回路，则对于结点集V的每个非空子集S均有W(G-S)￡|S|成立，其中W(G-S)是（G-S）中连通分支数。

5．汉密尔顿路存在的充分条件设G=<V，E>是具有n个结点的简单图，若在G中每一对结点度数之和大于等于n - 1，则在G中存在一条汉密尔顿路。

6．平面图的概念设G=<V，E>是一个无向图，如果能把G的所有结点与边画在平面上，并且使得任何两条边除端点外没有其他的交点，则称G是一个平面图（也称可平面图）.显然平面图的边与边只在结点处相交。

将平面图“图示在平面上”，有时也说成“将平面图嵌入一平面”。

7．平面图的面、边界、面的次数等概念设G是一个连通平面图，如果由图中的边所包围的一个区域内既不包含图的结点，也不包含图的边，则这个区域称为G的一个面，包围该面的所有边所构成的回路称为这个面的边界。

面r的边界的回路长度称为该面的次数，记为deg(r)。

欧拉图与汉密尔顿

欧拉图与汉密尔顿
欧拉图是满足每条边恰好出现一次的路径，而汉密尔顿图是满足每条边恰好出现一 次的回路。
欧拉路径是满足起点和终点相同，且每条边恰好出现一次的路径，而汉密尔顿回路 是满足起点和终点相同，且每条边恰好出现一次的回路。
欧拉图与汉密尔顿图的区别
欧拉图不一定是回路，而汉密尔顿图 一定是回路。
欧拉图可以有多条路径，而汉密尔顿 图只有一条路1
一个连通图存在欧拉回路当且仅当其 所有顶点的度均为偶数。
欧拉图的性质2
欧拉图的性质3
一个无向图存在欧拉回路当且仅当其 所有顶点的度都是偶数，或者只有一 个顶点的度是奇数，其余所有顶点的 度都是偶数。
如果一个连通图存在欧拉回路，那么 这个欧拉回路的长度一定是其边数的 两倍。
欧拉图与汉密尔顿
• 欧拉图 • 汉密尔顿图 • 欧拉图与汉密尔顿图的关系 • 欧拉图与汉密尔顿图的应用
目录
01
欧拉图
欧拉图的定义
欧拉图的定义：一个图如果存在一条路径，该路径经过图中的每条边恰好一次， 则称这条路径为欧拉路径，如果这个路径的起点和终点是同一点，则称为欧拉回 路。
欧拉回路是路径的子集，它从图的一个顶点出发，经过每条边一次且仅一次，最 后回到起始顶点。
欧拉图与汉密尔顿图在其他领域的应用
经济学
欧拉图与汉密尔顿图在经 济学中用于研究市场均衡、 供需关系等问题。
社会学
欧拉图与汉密尔顿图在社 会学中用于研究社会网络、 人际关系等问题。
生物学
欧拉图与汉密尔顿图在生 物学中用于研究生物分子 结构、基因调控网络等问 题。
感谢观看
THANKS
欧拉图只要求路径上的边不重复，而 汉密尔顿图要求路径上的边和节点都 不重复。
04
欧拉图与汉密尔顿图的应用

8.欧拉图与哈密顿图

8.欧拉图与哈密顿图

8.欧拉图与哈密顿图1.设G为n (n≥2)阶欧拉图，证明G是2-边连通图证明：存在一条欧拉回路，所以去掉其中任何一边e，该图G-e仍然是连通得，去掉两条边，该图可能是不连通的，所以λ(G)≥2,所以该图是2-边连通图2.设G为无向连通图，证明：G为欧拉图当且仅当G的每个块都是欧拉图证明：根据理题G为欧拉图当且仅当G可表示为若干个边不重的圈之并，易证若干个边不重的边，不一定是块。

块是指没有割点的极大连通子图证明：必要性如果G是欧拉图，根据定理8.1及其推论：G是若干边不相交的圈的并，G是欧拉图当且仅当G时连通的且G中无奇度顶点，所以我们在G中找块时，无非就是找割点两侧的圈，割点在每个圈中出现的所得的度数都是偶数，割点为V(V v11,v12,...,v1n,V,v21,v22,...v2nV,v3.....,V)其实很容易证明，割点两侧的圈都是连通的，且度数都为偶数,必要性得证充分性每个块都是欧拉图, 都是圈其中得割点是V1,V2...,Vn，那么V1,v11,v12,...,V2,v21,v22,...,v2n,V3,v31,v32,...v3n,..,V3....,V1得证我觉得思路是正确的，不过证明过程不是很严格（图这部分我还没有认真思考如何写出严格的步骤，以后我会继续研究证明过程！！·！）3.设G恰有2k(k≥1)个奇度顶点的连通图，证明G中存在K条边不重的简单通路P1,P2,…Pk，使得E(G)=U(I=1,k)E(Pi)证明：方法二对k做归纳法（1）k=1时，G为半欧拉图，因而存在欧拉通路P，则P为所求，所以结论为真。

（2）设k=r时，结论为真。

要证：k=r+1时结论为真。

设G的2k=2r+2个奇度顶点分别为V1,V2,…,Vr,Vr+1V1',V2',…,Vr',Vr+1'在Vr+1与Vr+1'之间加一条新边er+1=(Vr+1,Vr+1')，得图G'，则G'连通且有2r个奇度顶点。

《离散数学》第七章_图论-第3-4节

《离散数学》第七章_图论-第3-4节

图的可达性矩阵计算方法 （3） 无向图的可达性矩阵称为连通矩阵，也是对称的。 Warshall算法
例7-3.3 求右图中图G中的可达性矩 阵。 分析：先计算图的邻接矩阵A布尔乘法的的2、 v1
3、4、5次幂，然后做布尔加即可。
解：
v4
v2
v3 v5
P=A∨ A(2) ∨ A(3) ∨A(4)∨A(5)
图的可达性矩阵计算方法（2）
由邻接矩阵A求可达性矩阵P的另一方法： 将邻接矩阵A看作是布尔矩阵，矩阵的乘法运算和加 法运算中，元素之间的加法与乘法采用布尔运算 布尔乘：只有1∧1=1 布尔加：只有0∨0=0 计算过程： 1．由A，计算A2，A3，…，An。 2．计算P=A ∨ A2 ∨ … ∨ An P便是所要求的可达性矩阵。
v4
v3
v2
G中从结点v2到结点v3长度 为2通路数目为0，G中长 度为2的路（含回路）总数 为8，其中6条为回路。 G中从结点v2到结点v3长度 为3的通路数目为2， G中 长度为3的路（含回路）总

图的邻接矩阵的 应用 (2)计算结点vi与vj之间的距离。
中不为0的最小的L即为d<vi,vj>。
（一）有向图的可达性矩阵
可达性矩阵表明了图中任意两个结点间是否至少存在一条 路以及在任何结点上是否存在回路。
定义7-3.2 设简单有向图G=（V，E），其中V={v1， v2，…，vn }，n阶方阵P=（pij）nn ，称为图G的可达 性矩阵，其中第i行j列的元素
p ij =
1 1 1 1 P v3 1 1 v4 0 0 v5 0 0 v1 v2 1 1 1 1 1 1
0 1 A(G)= 1 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 1 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（5） （6） 图2 易知，图 2 中， （1） 、 （4）为欧拉图， （2） ， （5）为半欧拉图， （3） ， （6） 既不是欧拉图，也不是半欧拉图. 在（3） ， （6）中各至少加几条边才能 成为欧拉图？
（4）
练习:
(1) 判定下图中的图形是否能一笔画。
(2) 确定n取怎样的值，完全图Kn有一 条欧拉回路。
在一条汉密尔顿路。
例2 某地有5个风景点，若每个景点均有两条道路与 其他景点相通，问是否可经过每个景点一次而游完 这5处。
解 将景点作为结点，道路作为边，则得到一个有5
个结点的无向图。
由题意，对每个结点vi(i=1,2,3,4,5)有
deg(vi)=2。 则对任两点和均有 deg(vi) + deg(vj)=2 + 2 =4 = 5 – 1 所以此图有一条汉密尔顿路。即经过每个景点
——新华网 2006.1.10
2、汉密尔顿图
（1）定义4.2.1 给定图G，若存在一条路经过 图中的每个结点恰好一次，这条路称作汉密尔 顿路。若存在一条回路，经过图中的每个结点 恰好一次，这条回路称作汉密尔顿回路。 具有汉密尔顿回路的图称作汉密尔顿图。
下图存在一条汉密尔顿回路，它是汉密尔顿图
（2）定理4.2.1 若图G＝<V，E>具有汉密尔顿 回路，则对于结点集V的每个非空子集S均有W(GS)≤|S|，其中W(G-S)是G-S的连通分支数。
解： 完全图Kn每个结点的度数为n-1，要使 n-1为偶数，必须n为奇数。故当n为奇数时， 完全图Kn有欧拉回路。
可以将欧拉路和欧拉回路的概念推广到有向图中。
（5）定义4.1.2 给定有向图G，通过图中每边一次
且仅一次的一条单向路（回路），称作单向欧拉路
（回路）。 （6）定理4.1.2 有向图G为具有一条单向欧拉回路，
离散数学 Discrete Mathematics
第四章 几种特殊的图
4-1 欧拉图和汉密尔顿图
4-1 欧拉图和汉密尔顿图
要求： 1、理解欧拉图、汉密尔顿图的定义。 2、掌握欧拉图的判定方法。 3、会判断一些图不是汉密尔顿图。 4、熟悉一些欧拉图和汉密尔顿图。
学习本节要熟悉如下术语（9个）：
欧拉路、 欧拉回路、 欧拉图、 单向欧拉路、
此定理是必要条件，可以用来证明一个图不是
汉密尔顿图。 如右图，取S={v1,v4}， 则G-S有3个连通分支，
不满足W(G-S)≤|S|，故 该图不是汉密尔顿图。
说明：此定理是必要条件而不是充分条件。有的图 满足此必要条件，但也是非汉密尔顿图。
彼得森(Petersen)图
例如，著名的彼得森(Petersen)图， 在图中删去任一个结点或任意两个 结点，不能使它不连通；删去3个
本节内容到此结束
汉密尔顿图
范更华：歪打正着学了图论 灵光一闪发现定理
——科学中国人（2005）年度人物
汉密尔顿回路问题是图论最古老的研究课题之一，是至今未解决的世界 难题，在许多领域有着重要应用。经过多年艰苦攻克，范更华的这一项 目在这一问题的研究上开辟 了一条新的途径，证明若图中每对距离为2 的点中有一点的度数至少是图的点数的一半，则该图存在哈密尔顿回路。 了此成果引发了大量后续工作，以“范定理”、“范 条件”、“范类 型”被广泛引用而出现于多种国际权威学术刊物，并作为定理出现在国 外的教科书中。
仅一次到达另一结点。另一种就是从G的某个结点
出发，经过G的每一边一次仅一次再回到该结点。 上述两种情况分别可以由欧拉路和欧拉回路的判定 条件予以解决。
见137页图4.1.3
(b)为欧拉路，有从左下结点到右下结点的一笔画。 (a)为欧拉回路，可以从任一结点出发，一笔画回到原出发点。
（1）
（2）
（3）
当且仅当G连通，并且每个结点的入度等于出度。有
向图G有单向欧拉路，当且仅当G连通，并且恰有两
个结点的入度与出度不等，它们中一个的出度比入
度多1，另一个入度比出度多1。 例：P139 图4.1.4
二、汉密尔顿图（Hamilton）
几个问题 1. 在一个大城市，有很多取款机，那么，如何制定出一个最优的 路线，使运钞车过每个提款机一次就能运送完钱钞？ 货郎担问题旅行商人问题(TSP) 2. 考虑在七天内安排七门课程的考试，要求同一位教师所任教的 两门课程考试不安排在接连的两天里，如果教师所担任的课程 都不多于四门，则是否存在满足上述要求的考试安排方案？ 时间表问题 3. 国际象棋的跳马是否可以遍历其棋盘，即从任一格出发跳到每 一格仅一次并最后回到出发的棋盘格子？ 4. 在一个至少有5人出席的圆桌会议上（会议需要举行多次）， 为达到充分交流的目的，会议主持者希望每次会议每人两侧的 人均与前次不同，这是否可行？请应用图论知识进行论证。 5. 周游世界问题
（3）推论 无向图G具有一条欧拉回路，当且仅当G
连通且所有结点度数皆为偶数。
上述定理与推论可作为欧拉路和欧拉回路的判别
准则，因此哥尼斯堡七桥问题立即有了确切的否定答
案，因为从图中可以看到deg(A)＝5，deg(B)＝
deg(C)＝deg(D)=3，故欧拉回路必不存在。
（4）一笔画问题 要判定一个图G是否可一笔画出，有两种情况： 一是从图G中某一结点出发，经过图G的每一边一次

练习：
• 判定图是否存在汉密尔顿回路?
解： 在图中，有5个结点， 结点1的度数deg(1)＝3，deg(2)＝3， deg(3)＝4，deg(4)＝3，deg(5)＝3。由 于每一对结点的度数之和都大于5， 所以G中存在一条汉密尔顿回路，如 1—3—2—5—4—1。 1 2 3
4
5
作业 154页（6、7）
先分析无向图：
（1）定义4.1.1 如果无孤立结点图G上有一条经过G
的所有边一次且仅一次的路径，则称该路径为图G的 欧拉路。如果图G上有一条经过G边一次且仅一次的 的回路，则称该回路为图G的欧拉回路，具有欧拉回 路的图称为欧拉图。 （2）定理4.1.1 无向图G具有一条欧拉路，当且仅
当G连通，并且有零个或两个奇数度结点。
结点，最多只能得到有两个连通分支的子图；删去4个结
点，只能得到最多三个连通分支的子图；删去5个或5个以 上的结点，余下子图的结点数都不大于6，故必不能有5个 以上的连通分支数。所以该图满足W(G-S)≤|S|，但是可以 证明它是非汉密尔顿图。
下面的定理给出一个无向图具有汉密尔顿路的充分条件。
（3）定理4.2.2 设图G具有n个结点的简单图,如 果G中每一对结点度数之和大于等于n-1,则G中存
周游世界问题
与欧拉回路类似的是汉密尔顿回路。它是1859年汉密尔 顿首先提出的一个关于12面体的数学游戏：能否在下图中找 到一个回路，使它含有图中所有结点一次且仅一次？若把每 个结点看成一座城市，连接两个结点的边看成是交通线，那 么这个问题就变成能否找到一条旅行路线，使得沿着该旅行 路线经过每座城市恰好一次，再回到原来的出发地？他把这 个问题称为周游世界问题。
单向欧拉回路、 汉密尔顿路、 汉密尔顿回路、 汉密尔顿图、 图的闭包
掌握6个定理，1个推论。
一、欧拉图
1、哥尼斯堡七桥问题
C
A
B
D
七桥问题等价于在图中求一条回路，此回路 经过每条边一次且仅有一次。欧拉在1736年的论 文中提出了一条简单的准则，确定了哥尼斯堡七 桥一次而游完这5个景点。
例3 在七天内安排七门课程的考试，使得同一位教师 所任的两门课程不排在接连的两天中，试证明如果没 有教师担任多于四门课程，则符合上述要求的考试安
排总是可能的。
证明：设G为具有七个结点的图，每个结点对应于
一门课程考试，如果这两个结点对应的课程考试是由
不同教师担任的，那么这两个结点之间有一条边，因 为每个教师所任课程数不超过4，故每个结点的度数 至少是3，任两个结点的度数之和至少是6，故G总是 包含一条汉密尔顿路，它对应于一个七门考试课程的 一个适当的安排。

相关主题