18/25
集合与图论
哈密顿图的充分条件之一
若顶点vir-1,(r=2,3,...,k)与顶点vp相邻, 则G 有哈密顿圈v1v2...vi(r-1)vpvp-1...virv1.
因此vp至少与v1,v2,...,vp-1中的k个顶点不相邻. vp的度数为h,于是h≤p-1-k,从而k+h≤p-1, 因此k与h中至少有一个小于p/2,G 中有一个顶 点的度小于p/2.
集合与图论
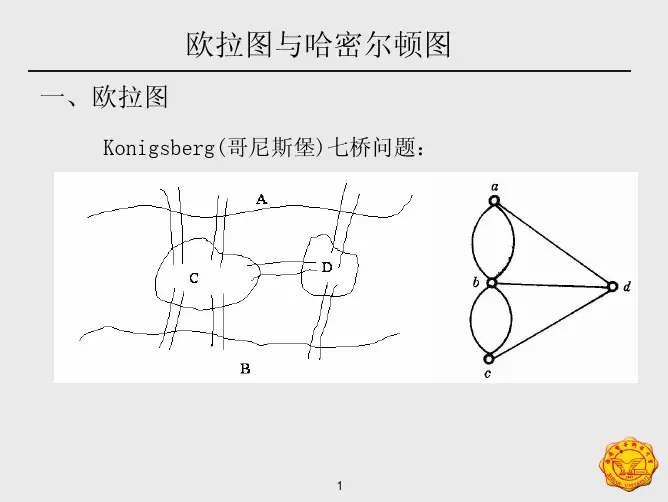
欧拉图的判别定理
若G2中还有边,则同样的方式,G2中有圈Z3,如 此等等,最后必得到一个图Gn,Gn中无边. 于是我们得到了G中的n个圈Z1,Z2,...,Zn,,它们是两 两无公共边的,因此,G的每条边在且仅在其中的一个 圈上,于是G的边集被划分为n个圈. 由于G是连通的,所以每个圈Zi至少与其余的某个 圈有公共顶点,从而图G由一些边不重的相互之间有公 6/25 共顶点的圈构成.
19/25
集合与图论
哈密顿图的充分条件之二
定理3 设G是有p(p≥3)个顶点的图,如果 对G的任意一对不相邻的顶点u和v,均有 degu+degv≥p, 则G是一个哈密顿图. 只需证明p(p≥3)个顶点的每个非哈密顿图中至少 有两个不相邻的顶点u和v,有degu+degv≤p-1即可. 刚才的证明中的v1,vp就满足这个性质.
22/25
集合与图论
实 例
例4:某次国际会议8人参加,已知每人至少与其余7 人中的4人有共同语言,问服务员能否将他们安排在 同一张圆桌就座,使得每个人都与两边的人交谈? 解 做无向图G=<V,E>, 其中 V={v| v为与会者}, E={{u,v} | u,vV且u与v有共同语言,且u v}. 易知G为无向图且vV, deg(v)4,于是,u,vV, 有 deg(u)+deg(v) 8,可知G为哈密顿图. 服务员在G中 找一条哈密顿圈C,按C中相邻关系安排座位即可.