下载文档原格式
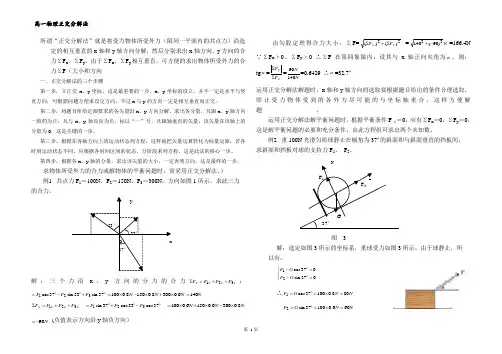
高一物理正交分解法所谓“正交分解法”就是将受力物体所受外力（限同一平面内的共点力）沿选定的相互垂直的x 轴和y 轴方向分解，然后分别求出x 轴方向、y 方向的合力ΣF x 、ΣF y ，由于ΣF x 、ΣF y 相互垂直，可方便的求出物体所受外力的合力ΣF （大小和方向一、正交分解法的三个步骤第一步，立正交 x 、y 坐标，这是最重要的一步，x 、y 坐标的设立，并不一定是水平与竖直方向，可根据问题方便来设定方向，不过x 与y 的方向一定是相互垂直而正交。
第二步，将题目所给定跟要求的各矢量沿x 、y 方向分解，求出各分量，凡跟x 、y 轴方向一致的为正；凡与x 、y 轴反向为负，标以“一”号，凡跟轴垂直的矢量，该矢量在该轴上的分量为0，这是关键的一步。
第三步，根据在各轴方向上的运动状态列方程，这样就把矢量运算转化为标量运算；若各时刻运动状态不同，应根据各时间区间的状态，分阶段来列方程。
这是此法的核心一步。
第四步，根据各x 、y 轴的分量，求出该矢量的大小，一定表明方向，这是最终的一步。
求物体所受外力的合力或解物体的平衡问题时，常采用正交分解法。
） 例1 共点力F 1＝100N ，F 2＝150N ，F 3＝300N ，方向如图1所示，求此三力 的合力。
y53°37°O x 37°解：三个力沿x ，y方向的分力的合力x x x x F F F F 321++=∑：︒+︒-︒=37sin 53sin 37cos 321F F F N N N 6.03008.01508.0100⨯+⨯-⨯=N 140= yy y y F F F F 321++=∑︒-︒+︒=37cos 53cos 37sin 321F F F NN N 8.03006.01506.0100⨯-⨯+⨯=N 90-= (负值表示方向沿y 轴负方向）由勾股定理得合力大小：ΣF=22)()(y x F F ∑+∑ =N 22)90(140-+=166.4N ∵ΣF x ﹥0、ΣF y ﹥0 ∴ΣF 在第四象限内，设其与x 轴正向夹角为α，则： tg α=xy F F ∑∑=NN14090=0.6429 ∴α=32.7º 运用正交分解法解题时，x 轴和y 轴方向的选取要根据题目给出的条件合理选取，即让受力物体受到的各外力尽可能的与坐标轴重合，这样方便解题 。
第一讲正交分解法知识点一：共点力及平衡条件共点力：物体同时受几个力的作用，如果这几个力都作用于物体的同一点或者它们的作用线交于同一点，这几个力叫共点力。
能简化成质点的物体受到的力可视为共点力。
平衡状态：物体保持静止．．．．．．状态．．．．或匀速直线运动注意：这里的静止需要二个条件，一是物体受到的合外力为零，二是物体的速度为零，仅速度为零时物体不一定处于静止状态，如物体做竖直上抛运动达到最高点时刻，物体速度为零，但物体不是处于静止状态，因为物体受到的合外力不为零。
共点力的平衡：如果物体受到共点力的作用，且处于平衡状态，就叫做共点力的平衡。
1.如图所示，小明用与水平方向成θ角的轻绳拉木箱，沿水平面做匀速直线运动，此时绳中拉力为F，则木箱所受合力大小为（）>A 0B FC FcosθD Fsinθ2、如图所示，一质量为m的物体沿倾角为θ的斜面匀速下滑。
下列说法正确的是（）A 物体所受合力的方向沿斜面向下B 斜面对物体的支持力等于物体的重力C 物体下滑速度越大，说明物体所受摩擦力越小D 斜面对物体的支持力和摩擦力的合力的方向竖直向上知识点二：共点力的处理方法——正交分解法!正交分解一般步骤：选定研究对象，并作出受力分析建立合适的直角坐标系（尽可能少分解力）将不在坐标轴上的力分解到坐标轴上列出平衡状态下x方向、y方向的方程求解：x方向上：F1x=F2x y方向上：F1y+F2y=G1.质量为m的木块在推力F作用下，在水平地面上做匀速运动（如图所示）。
已知木块与地面间的动摩擦因数为μ，那么木块受到的滑动摩擦力为下列各值的哪一个（）A μmgB μ（mg＋Fsinθ）-C μ（mg－Fsinθ）D Fcosθ2.物体放在粗糙的水平地面上，物体重50N，受到斜向上方向与水平面成300角的力F作用，F = 50N，物体仍然静止在地面上，如图所示，求：物体受到的摩擦力和地面的支持力分别是多少3.在图中，AB、AC两光滑斜面互相垂直，AC与水平面成30°.如把球O的重力G按照其作用效果分解，则两个分力的大小分别为（）A 12G，32G B33G，3G-C23G，22G D22G，32G4.甲、乙两人用绳子拉船，使船沿OO′方向航行，甲用1 000 N的力拉绳子，方向如图所示，要使船沿OO′方向航行，乙的拉力最小值为（）A 500 3 NB 500 NC 1 000 ND 400 N练习：1.质量为m的物体在恒力F作用下，F与水平方向之间的夹角为θ，沿天花板向右做匀速运动，物体与顶板间动摩擦因数为μ，则物体受摩擦力大小为多少&2.直角劈形木块（截面如图所示）的质量M=2kg，用外力F顶靠在竖直墙上。
高中物理正交分解讲解及解题方法步骤高中物理正交分解是一种常用的解题方法，主要用于解决涉及两个互相垂直方向的物理问题。
下面我将详细讲解正交分解的原理、应用和解题步骤。
一、正交分解的原理正交分解是将一个物理量沿着两个互相垂直的方向进行分解的方法。
在物理学中，很多物理量都可以用正交分解的方法进行求解，如力、速度、加速度等。
正交分解的原理基于矢量的分解和合成。
矢量是既有大小又有方向的量，可以沿任意方向进行分解和合成。
在正交分解中，我们将一个矢量沿两个互相垂直的方向进行分解，得到两个互相垂直的分量。
这两个分量是独立的，它们的大小和方向都可以单独求解。
二、正交分解的应用1.力的正交分解力的正交分解是解决力学问题的常用方法。
在解决涉及两个互相垂直方向的力的问题时，我们可以将力沿这两个方向进行分解，得到两个互相垂直的分力。
然后分别对这两个分力进行分析和求解，最后合成得到总力。
2.速度和加速度的正交分解在解决涉及速度和加速度的问题时，我们也可以使用正交分解的方法。
将速度或加速度沿两个互相垂直的方向进行分解，得到两个互相垂直的分速度或分加速度。
然后分别对这两个分速度或分加速度进行分析和求解，最后合成得到总速度或总加速度。
三、正交分解的解题步骤1.确定需要分解的物理量。
2.确定两个互相垂直的方向。
3.将物理量沿这两个方向进行分解，得到两个互相垂直的分量。
4.分别对这两个分量进行分析和求解。
5.最后将两个分量合成得到总物理量。
四、例题解析例题：一个物体在水平方向上受到两个力的作用，这两个力的大小分别为F1=10N和F2=20N，方向互相垂直。
求这个物体的合力大小和方向。
解题步骤：1.确定需要分解的物理量：合力。
2.确定两个互相垂直的方向：水平方向和竖直方向。
3.将合力沿这两个方向进行分解，得到两个互相垂直的分力：水平分力和竖直分力。
4.分别对这两个分力进行分析和求解：水平分力为F1=10N，竖直分力为F2=20N。
5.最后将两个分力合成得到总合力：F=√(F1²+F2²)=√(10²+20²)=√500N，方向为与水平方向成arctan(2)的夹角斜向上。
由勾股定理得合力大小：ΣF=22)()(y x F F ∑+∑ =N22)90(140-+=166.4N∵ΣF x ﹥0、ΣF y ﹥0 ∴ΣF 在第四象限内，设其与x 轴正向夹角为α，则： tg α=x yF F ∑∑=NN14090=0.6429 ∴α=32.7º运用正交分解法解题时，x 轴和y 轴方向的选取要根据题目给出的条件合理选取，即让受力物体受到的各外力尽可能的与坐标轴重合，这样方便解题 。
运用正交分解法解平衡问题时，根据平衡条件F 合＝0，应有ΣF x ＝0，ΣF y ＝0，这是解平衡问题的必要和充分条件，由此方程组可求出两个未知数。
例2 重100N 光滑匀质球静止在倾角为37º的斜面和与斜面垂直的挡板间， 求斜面和挡板对球的支持力F 1， F 2。
yF 1 xF 2G37°图 3解：选定如图3所示的坐标系，重球受力如图3所示。
由于球静止，所 以有：⎩⎨⎧=︒-=︒-037sin 037cos 21G F G F∴N N G F 808.010037cos 1=⨯=︒= N N G F 606.010037sin 2=⨯=︒=1．如图所示，用绳AO 和BO 吊起一个重100N 的物体，两绳AO 、BO 与竖直方向的夹角分别为30o 和40o ，求绳AO 和BO 对物体的拉力的大小。
2.如图所示，重力为500N的人通过跨过定滑轮的轻绳牵引重200N的物体，当绳与水平面成6 0o角时，物体静止，不计滑轮与绳的摩擦，求地面对人的支持力和摩擦力。
3. (8分)如图6所示，θ＝370，sin370＝0.6，cos370＝0.8。
箱子重G＝200N，箱子与地面的动摩擦因数μ＝0.30。
要匀速拉动箱子，拉力F为多大？4.（8分）如图，位于水平地面上的质量为M的小木块，在大小为F、方向与水平方向成a角的拉力作用下沿地面作匀速直线运动。
求：（1）地面对物体的支持力？（2）木块与地面之间的动摩擦因数？5．（6分）如图10所示，在倾角为α=37°的斜面上有一块竖直放置的档板，在档板和斜面之间放一个重力G=20N的光滑球，把球的重力沿垂直于斜面和垂直于档板的方向分解为力F1和F2，求这两个分力F1和F2的大小。
高一物理正交分解技巧
一般在力的分解时候用。
将一个已知力正交分解，就是先从它的起点化一个水平的X坐标轴；再从同一起点画一个垂直于那个水平轴的Y轴。
以力的终点作为这个矩形的另一个顶点，连接成四边形。
原来的那个斜向的力，就用正交法分解成了一个水平的力和一个垂直的力。
力的合成与分解的一般方法，但是在一些情况下，受力的方向没有规律，我们不好判断合力的方向，这时，我们可以采用正交分解求合力的方法。
(1)明确研究对象(或系统)；
(2)了解运动状态(题给出、暗示或判断、假设）；
(3)进行受力分析（按顺序，场力、弹力、摩擦力）；
(4)建立坐标,对力进行正交分解（有相对运动或相对运动趋势的特别是有加速度的，必需建一轴在这方向上）
(5)立方程，解之。
（有时还需∑M=0，这不属正交分解法）
简单点说,先把所有的力画出来,再找个(x,y)坐标系(找个利于求解的,比如竖直与水平,垂直与平行之类),然后把力分解到坐标系的方向,再利用坐标系方向的力("合力")加加减减求解就行了.用于求运动,比如匀速,加速之类的方法.
具体要看题目的情况。
正交分解思想在高中物理中的应用1、正交分解法：把同一矢量系的各个矢量向垂直的两个坐标轴（x 轴和y 轴）方向分解。
2、适用范围：所有矢量，比如高中阶段学的矢量：力、速度、位移、加速度、电场强度、磁感应强度等等。
3、基本原理：矢量的合成和分解法则，即平行四边形定则；先分解后合成，即为了合成而分解（欲合先分）。
一、正交分解思想在求合力中的应用【例1】如图所示，三个共点力F 1、F 2、F 3的大小分别为20N 、30N 、40N ，求这三个共点力的合力。
【答案】二、正交分解思想在求共点力平衡中的应用【例2】如图甲，质量为m 的木块静止在固定斜面上，已知斜面倾角为θ，重力加速度为g ，求木块所受摩擦力？【例3】如图乙，一个质量为m 的木块放在固定的粗糙斜面上，今对木块施一个既与斜面底边平行又与斜面平行的推力F ，木块处于静止状态。
已知斜面倾角为θ，重力加速度为g ，求木块所受摩擦力？【答案】甲θ乙【例4】如图所示，粗糙斜面P 固定在水平面上，斜面倾角为θ，在斜面上有一个小滑块Q 。
若给Q 一个水平向右的推力F ，无论推力为多大，Q 都不会向上滑动，则PQ 间的动摩擦因数( )A．不小于1tan θB．等于1tan θC ．等于tan θD ．不小于tan θ答案 A解析 对Q ，沿斜面向上的合外力F ′＝F cos θ－μ(F sin θ＋mg cos θ)－mg sin θ，整理为F ′＝(cos θ－μsin θ)F －(μcos θ＋sin θ)mg ，只有当F 的系数(cos θ－μsin θ)≤0时，F ′才不能大于0，即合外力不可能向上，滑块不可能向上滑动，解得μ≥1tan θ，所以答案为A 。
三、正交分解思想在求牛顿第二定律中的应用1、牛顿第二定律的分量式：F 合x =ma x ，F 合y =ma y ；2、为了减少矢量分解，建立坐标系时，确定x 轴正方向主要有以下两种方法：①分解力而不分解加速度，此方法一般规定加速度a 的方向为x 轴正方向；②分解加速度而不分解力，把加速度分解在x 轴和有轴上。
高一力的正交分解知识点高一力的正交分解是一种在线性代数中常用的运算方法，用于将一个向量分解为两个正交的向量的和。
正交是指两个向量的内积为零，即垂直于彼此。
正交分解的方法有很多，本文将介绍其中的两种常见方法：基底法和投影法。
1. 基底法基底法是一种将向量投影到基底上的方法，通过计算向量在基底上的投影系数，得到向量的正交分解。
首先，需要找到一个由正交向量组成的基底集合。
假设我们有一个向量v=(v1,v2,...,vn)，我们可以找到一个正交基底{u1,u2,...,un}，使得v可以表示为这个基底的线性组合，即v=a1u1+a2u2+...+anun。
其中，a1、a2、...、an是向量v在基底上的投影系数，可以通过内积的方法求解。
具体的求解步骤如下：（1）选择一组正交基底{u1,u2,...,un}，确保每个基底向量都与其它向量正交。
（2）计算向量v在每个基底向量上的投影系数ai，即ai=(v·ui) / (ui·ui)，其中·表示内积运算。
（3）将投影系数与对应的基底向量相乘，并相加得到分解后的向量：v=a1u1+a2u2+...+anun。
基底法的优点是计算简单，容易理解和应用。
但是需要预先确定正交基底集合，如果基底集合不合适，则无法进行正交分解。
2. 投影法投影法是一种通过将向量投影到另一个向量上的方法，实现向量的正交分解。
与基底法不同的是，投影法不需要预先确定正交基底集合，只需要一个与该向量垂直的向量即可。
假设我们有一个向量v=(v1,v2,...,vn)，我们可以找到一个与向量v垂直的向量u=(u1,u2,...,un)。
具体的求解步骤如下：（1）选择一个与向量v垂直的向量u，可以通过向量v减去其在u上的投影得到。
即，u=v-(v·u)u / (u·u)。
（2）计算向量v在向量u上的投影系数b，即b=(v·u) / (u·u)。
