高一物理必修1正交分解
- 格式:doc
- 大小:561.50 KB
- 文档页数:6
高一物理正交分解法所谓“正交分解法”就是将受力物体所受外力(限同一平面内的共点力)沿选定的相互垂直的x 轴和y 轴方向分解,然后分别求出x 轴方向、y 方向的合力ΣF x 、ΣF y ,由于ΣF x 、ΣF y 相互垂直,可方便的求出物体所受外力的合力ΣF (大小和方向一、正交分解法的三个步骤第一步,立正交 x 、y 坐标,这是最重要的一步,x 、y 坐标的设立,并不一定是水平与竖直方向,可根据问题方便来设定方向,不过x 与y 的方向一定是相互垂直而正交。
第二步,将题目所给定跟要求的各矢量沿x 、y 方向分解,求出各分量,凡跟x 、y 轴方向一致的为正;凡与x 、y 轴反向为负,标以“一”号,凡跟轴垂直的矢量,该矢量在该轴上的分量为0,这是关键的一步。
第三步,根据在各轴方向上的运动状态列方程,这样就把矢量运算转化为标量运算;若各时刻运动状态不同,应根据各时间区间的状态,分阶段来列方程。
这是此法的核心一步。
第四步,根据各x 、y 轴的分量,求出该矢量的大小,一定表明方向,这是最终的一步。
求物体所受外力的合力或解物体的平衡问题时,常采用正交分解法。
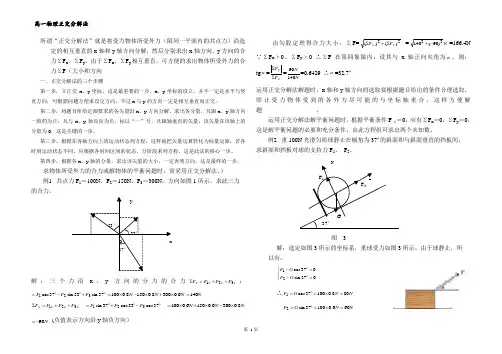
) 例1 共点力F 1=100N ,F 2=150N ,F 3=300N ,方向如图1所示,求此三力 的合力。
y53°37°O x 37°解:三个力沿x ,y方向的分力的合力x x x x F F F F 321++=∑:︒+︒-︒=37sin 53sin 37cos 321F F F N N N 6.03008.01508.0100⨯+⨯-⨯=N 140= yy y y F F F F 321++=∑︒-︒+︒=37cos 53cos 37sin 321F F F NN N 8.03006.01506.0100⨯-⨯+⨯=N 90-= (负值表示方向沿y 轴负方向)由勾股定理得合力大小:ΣF=22)()(y x F F ∑+∑ =N 22)90(140-+=166.4N ∵ΣF x ﹥0、ΣF y ﹥0 ∴ΣF 在第四象限内,设其与x 轴正向夹角为α,则: tg α=xy F F ∑∑=NN14090=0.6429 ∴α=32.7º 运用正交分解法解题时,x 轴和y 轴方向的选取要根据题目给出的条件合理选取,即让受力物体受到的各外力尽可能的与坐标轴重合,这样方便解题 。




正交分解法解平衡问题
班级 姓名
例1如图,氢气球被水平吹来的风吹成图示的情形,若测得绳子与水平面的夹角为37˚,已知气球受到空气的浮力为15N ,忽略氢气球的重力,sin 37˚=0.6,cos 37˚求:
①氢气球受到的水平风力多大?
②绳子对氢气球的拉力多大?
例2在水平地面上有一质量为10kg 的物体,它受到与水平方向成37˚斜向上的50N 的拉力作用,在水平方向做匀速直线运动,g=10m/s2,求物体与地面间的动摩擦因数 (sin370=0.6,cos370=0.8)
例3物体A 的质量为m ,斜面倾角α,斜面固定,现有一个水平力F
作用在A 上,物体A 恰能沿斜面匀速向上运动。
请对A 进行受力分析,
并利用正交分解法,写出平衡方程
课堂测评 如图所示,重50N 的物体在与水平方向成370角的拉力作用下在水平地面
上保持静止,F=30N 。
试求物体所受的支持力和摩擦力。
(cos370。




高一物理必修1第四章牛顿运动定律应用物体平衡正交分解法专题专项训练习题集【知识点梳理】1.物体受到三个以上共点力作用处于平衡状态时,利用正交分解法解决此类平衡问题,建立直角坐标系,把力分解在两条坐标轴上。
2.合理选取直角坐标系,通常情况把坐标系建立在物体的运动方向和垂直运动方向上,一般不分解摩擦力和支持力。
3.按照分解后的受力情况,分别写出两个垂直方向上合力为零的表达式,如果物体受滑动摩擦力再写出滑动摩擦力的公式,利用方程组求解即可。
4.临界状态:是从一种物理现象转变为另一种物理现象,或从一物理过程转入到另一物理过程的转折状态。
临界状态也可理解为“恰好出现”和“恰好不出现”某种现象的状态。
要从临界状态中看出已知的隐含的条件。
【典题训练】1.在水平路面上用绳子拉一只重110N的箱子,绳子和路面的夹角为37°,如图所示。
当绳子的拉力为50N,恰好使箱子匀速移动,求箱子和地面间的动摩擦因数。
(取sin370=0.6,cos370=0.8)2.如图所示,位于斜面上的物块M,在沿斜面向上的推力F作用下,处于静止状态,则斜面施于M的摩擦力()A.方向一定沿斜面向下B.方向可能沿斜面向下C.大小可能等于零D.大小一定不为零3.如图所示,位于斜面上的物块,在沿斜面向上的推力F作用下,处于静止状态,若推力F逐渐增大,则摩擦力大小变化情况说法正确的是()A.一定增大B.可能逐渐增大C.可能逐渐减小D.可能先减小后增大4.如图所示,人的质量为M,物块的质量为m,且M>m,若不计绳与滑轮的摩擦,则当人拉着绳向右跨出一步后,人和物仍保持静止,则下列说法中正确的是()A.地面对人的摩擦力减小B.地面对人的摩擦力增大C.人对地面的压力减小D.人对地面的作用力增大5.质量为m的物体放在倾角为α的斜面上,力F垂直于斜面作用在物体上,物体处于静止状态,如图所示。
下列说法中正确的是()A.力F越大,物体所受摩擦力越大B.力F越小,物体所受摩擦力越小C.力F越大,物体所受摩擦力可能越大,也可能越小6.如图所示,物体A在竖直向上的拉力F的作用下能静止在斜面上,则关于A受力的个数,下列说法中正确的是()A.A一定是受两个力作用B.A一定是受四个力作用C.A可能受三个力作用D.A不是受两个力作用就是受四个力作用7.质量为m的物体放在倾角为θ的斜面上,它跟斜面间的动摩擦因数为μ,在水平恒定的力F作用下,物体沿斜面向上匀速运动,则物体所受的摩擦力是()A.μmgcosθB.μ(mgcosθ+Fsinθ)C.(Fcosθ—mgsinθ) D.μ(mgcosθ-Fsinθ)8.如图所示,重量为40N的物体与竖直墙面间的动摩擦因数为μ=0.4,若用与水平方向夹角为θ=370斜向上的推力F=60N托住物体,物体处于静止状态。

F1F2 FOF1F2FO力的合成与分解1.力的合成(1)力的合成的本质就在于保证作用效果相同的前提下,用一个力的作用代替几个力的作用,这个力就是那几个力的“等效力”(合力)。
力的平行四边形定则是运用“等效”观点,通过试验总结出来的共点力的合成法则,它给出了寻求这种“等效代换”所遵循的规律。
(2)平行四边形定则可简化成三角形定则。
由三角形定则还可以得到一个有用的推论:假如n个力首尾相接组成一个封闭多边形,则这n 个力的合力为零。
(3)共点的两个力合力的大小范围是|F1-F2| ≤F合≤F1+F2(4)共点的三个力合力的最大值为三个力的大小之和,最小值可能为零。
2.力的分解(1)力的分解遵循平行四边形法则,力的分解相当于已知对角线求邻边。
(2)两个力的合力惟一确定,一个力的两个分力在无附加条件时,从理论上讲可分解为多数组分力,但在详细问题中,应依据力实际产生的效果来分解。
(3)几种有条件的力的分解①已知两个分力的方向,求两个分力的大小时,有唯一解。
②已知一个分力的大小和方向,求另一个分力的大小和方向时,有唯一解。
③已知两个分力的大小,求两个分力的方向时,其分解不惟一。
④已知一个分力的大小和另一个分力的方向,求这个分力的方向和另一个分力的大小时,其分解方法可能惟一,也可能不惟一。
(4)用力的矢量三角形定则分析力最小值的规律:①当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2取最小值的条件是两分力垂直。
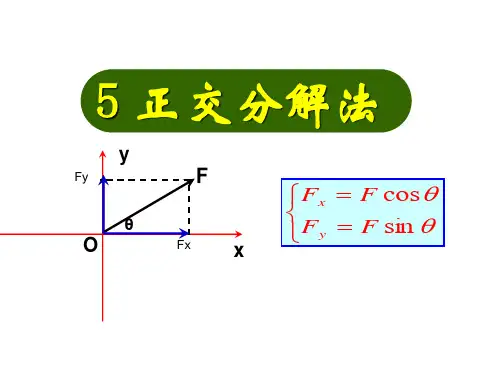
如图所示,F2的最小值为:F2min=F sinα②当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2取最小值的条件是:所求分力F2与合力F垂直,如图所示,F2的最小值为:F2min=F1sinα③当已知合力F的大小及一个分力F1的大小时,另一个分力F2取最小值的条件是:已知大小的分力F1与合力F同方向,F2的最小值为|F-F1|(5)正交分解法:把一个力分解成两个相互垂直的分力,这种分解方法称为正交分解法。
高一物理正交分解技巧
一般在力的分解时候用。
将一个已知力正交分解,就是先从它的起点化一个水平的X坐标轴;再从同一起点画一个垂直于那个水平轴的Y轴。
以力的终点作为这个矩形的另一个顶点,连接成四边形。
原来的那个斜向的力,就用正交法分解成了一个水平的力和一个垂直的力。
力的合成与分解的一般方法,但是在一些情况下,受力的方向没有规律,我们不好判断合力的方向,这时,我们可以采用正交分解求合力的方法。
(1)明确研究对象(或系统);
(2)了解运动状态(题给出、暗示或判断、假设);
(3)进行受力分析(按顺序,场力、弹力、摩擦力);
(4)建立坐标,对力进行正交分解(有相对运动或相对运动趋势的特别是有加速度的,必需建一轴在这方向上)
(5)立方程,解之。
(有时还需∑M=0,这不属正交分解法)
简单点说,先把所有的力画出来,再找个(x,y)坐标系(找个利于求解的,比如竖直与水平,垂直与平行之类),然后把力分解到坐标系的方向,再利用坐标系方向的力("合力")加加减减求解就行了.用于求运动,比如匀速,加速之类的方法.
具体要看题目的情况。
高一物理必修一公式大全总结力的合成与分解1.同一直线上力的合成同向:F=F1+F2,反向:F=F1-F2(F1>F2)2.互成角度力的合成:F=(F12+F22+2F1F2cosα)1/2(余弦定理)F1⊥F2时:F=(F12+F22)1/23.合力大小范围:|F1-F2|≤F≤|F1+F2|4.力的正交分解:Fx=Fcosβ,Fy=Fsinβ(β为合力与x轴之间的夹角tgβ=Fy/Fx)注:(1)力(矢量)的合成与分解遵循平行四边形定则;(2)合力与分力的关系是等效替代关系,可用合力替代分力的共同作用,反之也成立;(3)除公式法外,也可用作图法求解,此时要选择标度,严格作图;(4)F1与F2的值一定时,F1与F2的夹角(α角)越大,合力越小;(5)同一直线上力的合成,可沿直线取正方向,用正负号表示力的方向,化简为代数运算。
竖直上抛运动1.位移s=Vot-gt2/22.末速度Vt=Vo-gt(g=9.8m/s2≈10m/s2)3.有用推论Vt2-Vo2=-2gs4.上升高度Hm=Vo2/2g(抛出点算起)5.往返时间t=2Vo/g(从抛出落回原位置的时间)注:(1)全过程处理:是匀减速直线运动,以向上为正方向,加速度取负值;(2)分段处理:向上为匀减速直线运动,向下为自由落体运动,具有对称性;(3)上升与下落过程具有对称性,如在同点速度等值反向等。
匀变速直线运动1.速度Vt=Vo+at2.位移s=Vot+at?/2=V平t=Vt/2t3.有用推论Vt?-Vo?=2as4.平均速度V平=s/t(定义式)5.中间时刻速度Vt/2=V平=(Vt+Vo)/26.中间位置速度Vs/2=√[(Vo?+Vt?)/2]7.加速度a=(Vt-Vo)/t{以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0}8.实验用推论Δs=aT?{Δs为连续相邻相等时间(T)内位移之差}9.主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s=3.6km/h。
第一讲正交分解法
知识点一:共点力及平衡条件
共点力:物体同时受几个力的作用,如果这几个力都作用于物体的同一点或者它们的作用线交于同一点,这几个力叫共点力。
能简化成质点的物体受到的力可视为共点力。
平衡状态:物体保持静止
......状态
....或匀速直线运动
注意:这里的静止需要二个条件,一是物体受到的合外力为零,二是物体的速度为零,仅速度为零时物体不一定处于静止状态,如物体做竖直上抛运动达到最高点时刻,物体速度为零,但物体不是处于静止状态,因为物体受到的合外力不为零。
共点力的平衡:如果物体受到共点力的作用,且处于平衡状态,就叫做共点力的平衡。
1.如图所示,小明用与水平方向成θ角的轻绳拉木箱,沿水平面做匀速直线运动,
此时绳中拉力为F,则木箱所受合力大小为()
>
A 0
B F
C Fcosθ
D Fsinθ
2、如图所示,一质量为m的物体沿倾角为θ的斜面匀速下滑。
下列说法正确的是()
A 物体所受合力的方向沿斜面向下
B 斜面对物体的支持力等于物体的重力
C 物体下滑速度越大,说明物体所受摩擦力越小
D 斜面对物体的支持力和摩擦力的合力的方向竖直向上
知识点二:共点力的处理方法——正交分解法
!
正交分解一般步骤:
选定研究对象,并作出受力分析
建立合适的直角坐标系(尽可能少分解力)
将不在坐标轴上的力分解到坐标轴上
列出平衡状态下x方向、y方向的方程求解:x方向上:F1x=F2x y方向上:F1y+F2y=G
1.质量为m的木块在推力F作用下,在水平地面上做匀速运动(如图所示)。
已知木块与地面间的动摩擦因
数为μ,那么木块受到的滑动摩擦力为下列各值的哪一个()
A μmg
B μ(mg+Fsinθ)
-
C μ(mg-Fsinθ)
D Fcosθ
2.物体放在粗糙的水平地面上,物体重50N,受到斜向上方向与水平面成300角的力F作用,F = 50N,物体仍
然静止在地面上,如图所示,求:物体受到的摩擦力和地面的支持力分别是多少
3.在图中,AB、AC两光滑斜面互相垂直,AC与水平面成30°.如把球O的重力G按照其作用效果分解,则两个
分力的大小分别为()
A 1
2G,
3
2G B
3
3G,3G
-
C
2
3G,
2
2G D
2
2G,
3
2G
4.甲、乙两人用绳子拉船,使船沿OO′方向航行,甲用1 000 N的力拉绳子,方向如图所示,要使船沿OO′方
向航行,乙的拉力最小值为()
A 500 3 N
B 500 N
C 1 000 N
D 400 N
练习:
1.质量为m的物体在恒力F作用下,F与水平方向之间的夹角为θ,沿天花板向右做匀速运动,物体与顶板间
动摩擦因数为μ,则物体受摩擦力大小为多少
&
2.直角劈形木块(截面如图所示)的质量M=2kg,用外力F顶靠在竖直墙上。
已知木块与墙之间的最大静摩擦
力和木块对墙的压力成正比,即f m = kF N,比例系数k=。
则垂直作用于木块BC 边上的外力F应取何值木块保持静止。
(g =10 m/s2,sin 37°=0. 6,cos 37°=)
3.如图所示,一重为50N的物体放在倾角为37°的斜面上,沿斜面向下轻轻推一下物体,
$
物体刚好能沿斜面匀速下滑,sin37°=,cos37°=。
求:
(1)斜面对物体的支持力的大小;
(2)物体所受的摩擦力的大小;
(3)物体与斜面间的动摩擦因数。
4.如图,重为500N的人通过跨过定滑轮的轻绳牵引中200N的物体,
当绳与水平面成60度角时,物体静止,不计滑轮与绳的摩擦,
;
求地面对人的支持力和摩擦力。
5.如图所示,物体A质量为2kg,与斜面间摩擦因数为,若要使A在斜面上静止,物体B质量的最大值和最小
值是多少
'
6.如图所示,在光滑的斜面上用细绳吊着一个所受重力G=3N的小球,在图示情形下
小球处于静止状态,求此时绳对球的拉力大小及斜面给球的支持力大小。
7.如图,物体的质量为m,将它置于倾角为30°的光滑斜面上,受到外力F作用且当力F与
斜面的夹角θ由0°增大到60°的过程中,物体始终保持静止状态,则力F的大小
()
\
A 不变
B 一直增大
C 先减小后增大
D 先增大后减小
8.放在水平地面上的物块,受到一个与水平方向成α角的斜向下的力F的作用,物块在水平地面上做匀速直线
运动,如图所示,如果保持力F的大小变,而使力F与水平方向的夹角α减小,那么地面受到的压力N和物块受到的摩擦力f的变化情况是()
A N变大,f变小
B N变小,f变大
C N变小,f变小
D N变大,f变大
9.如图所示,质量m=5kg的物体,置于倾角θ=30°的粗糙斜面块上,用一平行于斜面的大小为30N的力推物体,
使其沿斜面向上匀速运动。
求地面对斜面块M的静摩擦力。
,
10.如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O。
轻绳
OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方
向的夹角θ=37°,物体甲、乙均处于静止状态。
(已知:sin 37°=,cos 37°=,tan 37°=,g取10 N/kg。
)求:
}
(1)轻绳OA、OB受到的拉力各多大(试用三种方法求解)
(2)物体乙受到的摩擦力多大方向如何
|
知识点三:共点力作用下物体的平衡条件
共点力作用下物体的平衡条件:物体受到的合外力为零。
即F合=0
1.如图所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为10kg的物体,∠ACB=30°;轻杆
HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°角,轻杆的G点用细绳FG拉住一个质量也为10kg的物体,g=10m/s2,求:
2.(1)轻绳AC段的张力FAC与细绳EG的张力FEG之比;
(2)横梁BC对C端的支持力大小和方向;
(3)轻杆HG对G端的支持力大小和方向。
;
3.*
4.如图所示,重力G1=8N的砝码挂在绳PA和PB的结点上,PA偏离竖直方向37°角,PB在水平方向,且连在
所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:
5.(1)绳PB上的拉力大小;
6.(2)木块所受斜面的弹力与摩擦力大小及方向。
1.:
2.如图所示,质量为m的等边三棱柱静止在水平放置的斜面上.已知三棱柱与斜面之间的动摩擦因数为μ,斜
面的倾角为30°,则斜面对三棱柱的支持力与摩擦力的大小分别为()
A
3
2mg和
1
2mg B
1
2mg和
3
2mg
C 1
2mg和
1
2μmg D
3
2mg和
3
2mg
3.如图所示,A、B两球完全相同,质量均为m,用两根等长的细线悬挂在O点,两球之间连着一根轻质弹簧,
静止不动时,两根细线之间的夹角为θ,则弹簧的弹力为()
A 2mg tan θ
B mg tan θ
C 2mg tan θ
2 D mg tan
θ
2
4.]
5.如图所示,一架直升机通过轻绳打捞海中物体,物体质量为m,由于流动的海水对物体产生水平方向的冲击,
使轻绳张紧且偏离竖直方向,当直升机相对地面静止时,绳子与竖直方向成θ角,已知物体所受的浮力不能忽略.下列说法正确的是()
A 绳子的拉力为mg
cos θ
B 绳子的拉力一定大于mg
C 物体受到海水的水平方向的作用力等于绳子的拉力
D 物体受到海水的水平方向的作用力小于绳子的拉力
6.如图所示,一个质量为m=的物体,放在倾角为θ=30°的斜面上静止不动,若用竖直向上的力F=提物体,
物体仍静止(g=10m/s2),下述结论正确的是()
A 物体受到的合外力减小
B 物体受到的摩擦力减小
C 斜面受到的压力减小
D 物体对斜面的作用力减小
7.质量为3kg的物体,放在倾角为30°的斜面上恰能匀速下滑,若要使该物体沿斜面匀速上滑,需对物体施加
多大的沿斜面向上的力
8.如图所示,质量为m1=的物体甲通过两段轻绳和一个轻质细弹簧悬挂在结点O。
轻绳OB水平且B端与放置
在水平面上质量为m2=的物体乙相连,轻弹簧OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态,弹簧的劲度系数为k=500N/m.(sin37°=,cos37°=,g取10m/s2)求:
9.(1)物体乙受到的摩擦力的大小与方向;
10.(2)轻弹簧的伸长量。