清华大学控制工程基础-控制系统的校正综合
- 格式:ppt
- 大小:623.50 KB
- 文档页数:13









清华大学822控制工程基础考研参考书目、考研真题、复试分数线822控制工程基础课程介绍本书是高等学校机械工程及自动化(机械设计制造及其自动化)专业系列教材之一,也是教育部新世纪网络课程的主要参考书。
内容简介全书共分8章:第1章控制系统的基本概念,第2章数学模型,第3章时域分析法,第4章频域分析法,第5章控制系统的设计和校正,第6章线性离散系统,第7章状态空间分析法,第8章控制系统的应用和分析。
书末附有5个附录。
每章附有习题,附录E有习题参考答案。
本书的特点是:淡化经典控制与现代控制的界限,突出方法论;重点阐述共性问题,适应拓宽专业口径的需要;不苛求严格的数学推证,从直观的物理概念出发分析问题、解决问题;特别重视工程应用,除每章附有较多机、电、液、气方面的例题外,还专辟一章介绍控制理论在工程中应用的成功实例;取材新颖,采用MATLAB等先进软件分析和设计系统;编写体系符合教学规律,好教易学;传授科学知识与培养创新能力并重。
内容简介本书以介绍工程上广为应用的经典控制论为主,使读者学会信息处理和系统分析与综合的基本方法。
同时,书中还简要介绍了非线性系统、计算机采样控制系统和控制系统计算机辅助分析的基本方法,以使读者建立起这方面的基本概念。
全书共九章,包括系统的数学模型、时域响应分析、频域响应分析、稳定性分析、误差分析、系统的综合与校正、非线性系统和计算机采样控制系统。
本书适合于机械设计制造及自动化专业、材料成型与控制工程专业。
本书为普通高等教育“十一五”国家级规划教材。
本书主要介绍工程中广为应用的经典控制理论和现代控制理论中控制系统分析与综合的基本方法。
全书共分十章:前六章属于经典控制理论国的线性定常连续控制系统问题,阐明了自动控制的三个基本问题,即模型、分析和控制;第七章和第八章分别为非线性系统及机采样控制系统;第九章为现代控制理论基础;第十章为典型控制系统的分析与设计实例。
本书总结了编者多年教学经验,且参考国内外教材特点,精选内容;叙述透彻,易教易学;强调基本概念和工程背景,适应面宽;正文中穿插有较多的例题,附有大量的习题(部分有答案),便于读者自学。

清华大学《控制工程基础》课件-5第一篇:清华大学《控制工程基础》课件-5由此得数字PID调节器的脉冲传递函数为系统的闭环传递函数为系统在单位阶跃输入时输出量的稳态值为由该例可见,由于积分的控制作用,对于单位阶跃输入,稳态误差为零。
由于微分控制作用,系统的动态特性得到很大改善,调节时间缩短,超调量减小。
●PID控制器参数的调整方法1)极点配置法将系统闭环极点配置在希望极点上,利用解析法确定PID参数。
2)瞬态响应法如果被控对象的阶跃响应如下图所示,其瞬态响应曲线的最大斜率为,时延为根据和可确定P,PI和PID控制器的参数。
3)极限灵敏度法这种方法要求首先用比例控制器来控制系统,逐步增大控制器增益,直到闭环系统达到稳定的边缘,系统处于恒幅振荡状态,测出控制器的增益和系统振荡周期。
根据这两个参数就可以确定控制器的参数。
数字PID控制器的改进如果单纯地用数字PID控制器去模仿模拟调节器,效果是有限的。
充分发挥计算机运算速度快、逻辑判断功能强、编程灵活等优势,才能达到更好的性能。
(1)积分项的改进(ⅰ)积分分离在一般的PID控制中,当有较大的扰动或大幅度改变给定值时,由于此时有较大的偏差,以及系统有惯性和滞后,故在积分项的作用下,往往会产生较大的超调和长时间的波动。
特别对于变化缓慢的过程,这一现象更为严重。
为此,可采用积分分离措施,即偏差较大时,取消积分作用;当偏差较小时才将积分作用投入。
(ⅱ)抗积分饱和因长时间出现偏差或偏差较大,计算出的控制量有可能溢出,或小于零。
作为防止积分饱和的办法之一,可对计算出的控制量u(k)限幅,同时,把积分作用切除掉。
(iii)消除积分不灵敏区由于计算机字长的限制,当运算结果小于字长所能表示的数的精度时,计算机就作为“零”将此数丢掉。
当计算机的运行字长较短,采样周期T也短,而积分时间又较长时,容易出现小于字长的精度而丢数,此积分作用消失,称为积分不灵敏区。
为了消除积分不灵敏区,通常采用以下措施:①增加A/D转换位数,加长运算字长,这样可以提高运算精度。
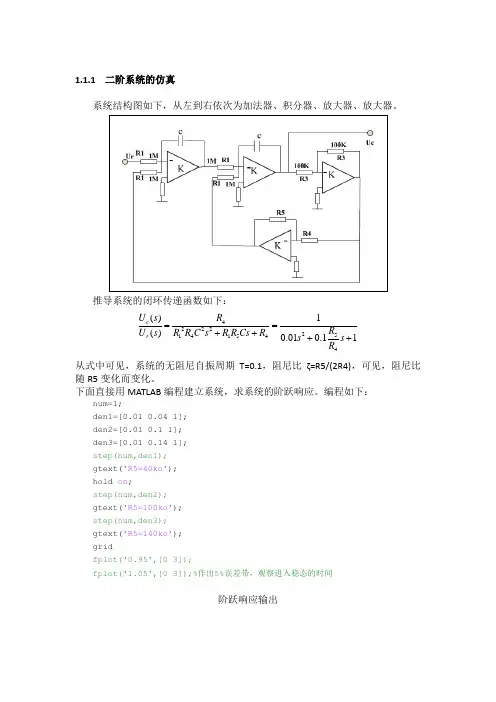
1.1.1 二阶系统的仿真系统结构图如下,从左到右依次为加法器、积分器、放大器、放大器。
推导系统的闭环传递函数如下:422225141544()1()0.010.11c r U s R R U s R R C s R R Cs R s s R ==++++从式中可见,系统的无阻尼自振周期T=0.1,阻尼比ζ=R5/(2R4),可见,阻尼比随R5变化而变化。
下面直接用MATLAB 编程建立系统,求系统的阶跃响应。
编程如下:num=1;den1=[0.01 0.04 1]; den2=[0.01 0.1 1]; den3=[0.01 0.14 1]; step(num,den1); gtext('R5=40ko'); hold on ;step(num,den2); gtext('R5=100ko'); step(num,den3); gtext('R5=140ko'); gridfplot('0.95',[0 3]);fplot('1.05',[0 3]);%作出5%误差带,观察进入稳态的时间阶跃响应输出425114541()()0.010.1R G s R R C R R Cs R s sR ==++编程建立系统,可以得到系统的开环伯德图和乃氏图,编程如下:num=1;den1=[0.01 0.04 0]; den2=[0.01 0.1 0]; den3=[0.01 0.14 0]; %bode(num,den1); nyquist(num,den1); gtext('R5=40ko'); hold on ;%bode(num,den2); nyquist(num,den2); gtext('R5=100ko'); %bode(num,den3); nyquist(num,den3); gtext('R5=140ko');grid系统开环伯德图系统开环乃氏图同样由系统闭环传递函数建立闭环系统模型,可以作出系统的闭环伯德图与乃氏图。