控制工程基础第3版课后题答案-清华大学出版

控制工程基础第三章参考答案1. 请问什么是系统的时滞？系统的时滞是指系统输入与响应之间的时间延迟。

在许多实际的控制系统中，输出变量的改变并不立即反映在系统的输入上，而是有一定的延迟。

这种延迟就是系统的时滞。

2. 请简述控制系统的稳态误差。

控制系统的稳态误差是指在稳态下，输出与期望值之间的差别。

稳态误差可以分为零稳态误差和非零稳态误差。

零稳态误差是指当输入值为常数时，输出值与期望值之间的差别；非零稳态误差是指当输入值为非常数时，输出值与期望值之间的差别。

3. 请解释积分环节在控制系统中的作用。

积分环节在控制系统中的作用是消除稳态误差，尤其对于常量输入的情况。

当系统存在零稳态误差时，引入积分环节可以通过积累误差信号来逐渐减小误差，以达到稳定的目标。

积分环节还可以提高系统的灵敏度，增强系统的抗干扰能力。

4. 请简要说明先行环节的作用。

先行环节是在系统前面加入的一个环节，其作用是预先对输入信号进行处理，以改善系统的性能。

常见的先行环节包括微分环节和预估环节。

微分环节可以提高系统的动态响应速度，并减小系统超调量；预估环节可以通过估计未来的输入值来增强系统的鲁棒性。

5. 请解释滞后环节在控制系统中的作用。

滞后环节在控制系统中的作用是补偿相位滞后，改善系统的相位特性。

它可以有效提高系统的稳定性和抗干扰能力，减小系统的超调量和震荡现象。

滞后环节常用于降低系统的低频增益，使系统在低频段的响应更加平滑和稳定。

6. 什么是校正环节？请简要说明其作用。

校正环节是指在控制系统中用于校正输出与期望值之间差别的环节。

它通过调整系统的增益、相位和延迟等参数，使得系统的输出能够与期望值更加接近。

校正环节起到了提高系统性能、降低误差和稳定系统的作用。

7. 请解释反馈控制在控制系统中的作用。

反馈控制是一种常见的控制策略，它根据系统的输出信号与期望值之间的差别，调整系统的输入信号，以实现期望的控制目标。

反馈控制可以有效补偿系统的非线性特性、时滞和干扰等因素，提高系统的稳定性和鲁棒性。

控制工程基础第三版课后答案第一章1.1 分析控制系统的对象控制系统的对象通常指的是待控制的物理系统或过程。

在分析控制系统对象时，首先需要了解系统的动态特性。

为了分析控制系统的特性，我们可以通过选取一个合适的数学模型来描述物理系统的动态行为。

一种常用的方法是通过微分方程来描述系统的动态特性。

例如，对于一个简单的电路系统，可以使用基尔霍夫电流定律和基尔霍夫电压定律来建立描述电路中电流和电压之间关系的微分方程。

然后，通过求解这个微分方程，我们可以得到系统的传递函数。

另外，我们还可以使用频域分析的方法来分析控制系统的对象。

通过对信号的频谱进行分析，我们可以得到系统的频率响应。

1.2 常见的控制系统对象控制系统的对象存在各种各样的形式，下面列举了一些常见的控制系统对象：•机械系统：例如机器人、汽车悬挂系统等。

•电气系统：例如电路、电机等。

•热力系统：例如锅炉、冷却系统等。

•化工系统：例如反应器、蒸馏塔等。

针对不同的控制系统对象，我们需要选择合适的数学模型来描述其动态特性，并进一步分析系统的稳定性、性能等指标。

第二章2.1 控制系统的数学模型控制系统的数学模型描述了物理系统的动态特性和输入与输出之间的关系。

常见的控制系统数学模型包括：•模型中几何图形法：通过几何图形来描述系统的动态特性。

•传递函数法：采用以系统输入和输出的转移函数来描述系统的动态特性。

•状态方程法：将系统的状态变量与输入变量和输出变量之间的关系用一组偏微分方程或代数方程来描述。

在使用这些模型时，我们可以选择合适的数学工具进行分析和求解，例如微积分、线性代数等。

2.2 传递函数的定义和性质传递函数是描述控制系统输入输出关系的数学函数，通常用G(s)表示。

传递函数的定义和性质如下：•定义：传递函数G(s)是系统输出Y(s)和输入U(s)之间的比值，即G(s) = Y(s)/U(s)。

•零点和极点：传递函数可以有零点和极点，零点是使得传递函数为零的s值，极点是使得传递函数为无穷大的s值。

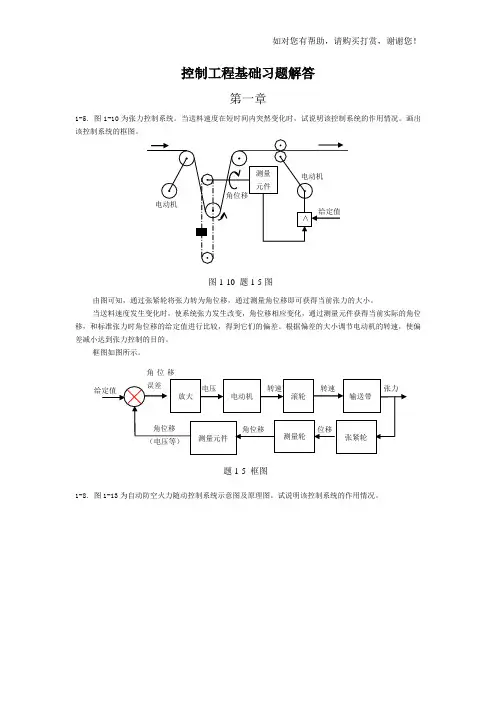
控制工程基础习题解答第一章1-5．图1-10为张力控制系统。

当送料速度在短时间内突然变化时，试说明该控制系统的作用情况。

画出该控制系统的框图。

图1-10 题1-5图由图可知，通过张紧轮将张力转为角位移，通过测量角位移即可获得当前张力的大小。

当送料速度发生变化时，使系统张力发生改变，角位移相应变化，通过测量元件获得当前实际的角位移，和标准张力时角位移的给定值进行比较，得到它们的偏差。

根据偏差的大小调节电动机的转速，使偏差减小达到张力控制的目的。

框图如图所示。

角位移题1-5 框图1-8．图1-13为自动防空火力随动控制系统示意图及原理图。

试说明该控制系统的作用情况。

该系统由两个自动控制系统串联而成：跟踪控制系统和瞄准控制系统，由跟踪控制系统获得目标的方位角和仰角，经过计算机进行弹道计算后给出火炮瞄准命令作为瞄准系统的给定值，瞄准系统控制火炮的水平旋转和垂直旋转实现瞄准。

跟踪控制系统根据敏感元件的输出获得对目标的跟踪误差，由此调整视线方向，保持敏感元件的最大输出，使视线始终对准目标，实现自动跟踪的功能。

瞄准系统分别由仰角伺服控制系统和方向角伺服控制系统并联组成，根据计算机给出的火炮瞄准命令，和仰角测量装置或水平方向角测量装置获得的火炮实际方位角比较，获得瞄准误差，通过定位伺服机构调整火炮瞄准的角度，实现火炮自动瞄准的功能。

控制工程基础习题解答第二章2-2．试求下列函数的拉氏变换，假定当t<0时，f(t)=0。

(3).()t e t f t 10cos 5.0-=解：()[][]()1005.05.010cos 25.0+++==-s s t e L t f Lt(5).()⎪⎭⎫ ⎝⎛+=35sin πt t f图1-13 题1-8图敏感元件解：()[]()252355cos 235sin 2135sin 2++=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s st t L t L t f Lπ2-6．试求下列函数的拉氏反变换。

控制工程基础习题解答第一章1-1．控制论的中心思想是什么？简述其发展过程。

维纳（N.Wiener）在“控制论——关于在动物和机器中控制和通讯的科学”中提出了控制论所具有的信息、反馈与控制三个要素，这就是控制论的中心思想控制论的发展经历了控制论的起步、经典控制理论发展和成熟、现代控制理论的发展、大系统理论和智能控制理论的发展等阶段。

具体表现为：1．1765年瓦特（Jams Watt）发明了蒸汽机，1788年发明了蒸汽机离心式飞球调速器，2．1868年麦克斯威尔（J.C.Maxwell）发表“论调速器”文章；从理论上加以提高，并首先提出了“反馈控制”的概念；3．劳斯（E.J.Routh）等提出了有关线性系统稳定性的判据4．20世纪30年代奈奎斯特（H.Nyquist）的稳定性判据，伯德（H.W.Bode）的负反馈放大器；5．二次世界大仗期间不断改进的飞机、火炮及雷达等，工业生产自动化程度也得到提高；6．1948年维纳（N.Wiener）通过研究火炮自动控制系统，发表了著名的“控制论—关于在动物和机器中控制和通讯的科学”一文，奠定了控制论这门学科的基础，提出了控制论所具有的信息、反馈与控制三要素；7．1954年钱学森发表“工程控制论”8．50年代末开始由于技术的进步和发展需要，并随着计算机技术的快速发展，使得现代控制理论发展很快，并逐渐形成了一些体系和新的分支。

9．当前现代控制理论正向智能化方向发展，同时正向非工程领域扩展（如生物系统、医学系统、经济系统、社会系统等），1-2．试述控制系统的工作原理。

控制系统就是使系统中的某些参量能按照要求保持恒定或按一定规律变化。

它可分为人工控制系统（一般为开环控制系统）和自动控制系统（反馈控制系统）。

人工控制系统就是由人来对参量进行控制和调整的系统。

自动控制系统就是能根据要求自动控制和调整参量的系统，系统在受到干扰时还能自动保持正确的输出。

它们的基本工作原理就是测量输出、求出偏差、再用偏差去纠正偏差。

控制工程基础-第3版课后题答案-清华大学出版控制工程基础课后习题 清华大学出版社亲 抄而不思则殆奥第一章1-1解：（1）B （2） B （3）B （4）A 1-2解：第二章2-1 解：（1）: )](12[)](1[)](5[)]()4[()(t L t t L t L t t L S F ⋅+⋅++=δδ S SS S 215215022++=+++= （2）: )25(253)(2++=s s S F（3）: 11)(2++=-s e S F sπ（4）:)}(1)6(1)]6(2cos 4{[)(5t e t t L S F t ⋅+-⋅-=-ππ5144512426226+++=+++=--S s Se S s Se s s ππ（5）:Se S e S F ss 226600)(--+=+++=（6）:)]4(1)90453cos(6[)(π-⋅--=t t L S F9636)]4(1)4(3cos 6[24224+=+=-⋅-=--S SeS Se t t L S S ππππ（7）: )](18sin 25.0)(18cos [)(66t t e t t e L S F t t ⋅+⋅=--1001288)6(28)6(622222+++=++++++=S S S S S S（8）: 99)20(52022)(262++++++=-s es s S F s π2-2 解：（1）: )(1)2()3221()(321t e e S S L t f t t ⋅+-=+++-=--- （2）: )(12sin 21)(t t t f ⋅=（3）: )(1)2sin 212(cos )(t t t e t f t ⋅+=（4）: )1(1)1()(11-⋅=-=---t e S e L t f t s（5）: )(1)22()(2t e e te t f t t t ⋅-+-=---（6）: )(1215sin 15158))215()21(21515158()(2221t t e S L t f t⋅=++⋅=-- （7）: )(1)3sin 313(cos )(t t t t f ⋅+=2-3 解：（1） 对原方程取拉氏变换，得：SS X x S SX x Sx S X S 1)(8)]0()([6)0()0()(2=+-+--⋅• 将初始条件代入，得：61)()86(1)(86)(6)(22++=++=+-+-S SS X S S SS X S SX S S X S48724781)86(16)(22+-++=++++=S S S S S S S S S X 取拉氏反变换，得：t t e e t x 42874781)(---+=（2） 当t=0时，将初始条件50)0(=•x 代入方程，得：50+100x(0)＝300则x(0)=2.5对原方程取拉氏变换，得： sx(s)-x(0)+100x(s)=300/s 将x(0)=2.5代入，得：S300100X(S)2.5-SX(S)=+ 1005.03100)S(S 3002.5S X(S)+-=++=s s取拉氏反变换，得：-100t 0.5e -3x(t)=2-4解：该曲线表示的函数为：)0002.0(16)(-⋅=t t u则其拉氏变换为：se s U s 0002.06)(-=2-5 解：)0()0()(3)(2)(2)(30100==+=+i i x y t x dtt dx t y dt t dy 将上式拉氏变换，得：2332)()()()32()()23()(3)(2)(2)(30000++=+=++=+S S S X S Y S X S S Y S S X S SX S Y S SY i i i i23-S 32-S Z p ==∴零点极点又当 时)(1)(t t x i =S S X i 1)(=SS S S X S X S Y S Y i i 12332)()()()(00⋅++=⋅= 3212332)()0(2312332)()(limlim lim lim 000000=⋅++⋅=⋅=∴=⋅++⋅=⋅=∞∴∞→∞→→→S S S S S Y S y S S S S S Y S y s s s s2-6 解：（a ）传递函数：132123233321123233321232333211111H G G G H G G H G G G G H H G G H G G G G H G G H G G G G R C+++=⋅++⋅+++⋅=（b ）传递函数：（ｃ）传递函数：（ｄ）传递函数：32121212211211H G G H H G G H G H G G G R C++++=2-7解：通过方块图的变换，系统可等价为下图：2-8解：2-92-10解：（a）（b）（c）2-11解：（a）（b）（c）（d）2-17 解：第三章3-1解：3-23-3解：3-53-6 解：3-7 解：3-8 解：3-9 解：3-103-113-13 解：3-14解：3-17 解：3-183-19 解：3-20解：3-22解：3-23 解：3-243-28 解：3-31 解：第四章4-3解：4-4解：4-5 解：4-74-10 解：4-16解：4-18 解：第五章5-15-75-85-115-125-145-16 解：5-18 解：5-19 解：5-20 解：5-25 解：第六章6-1（1）（2）（3）（4）＝0 6-2解：（1）6-4 解：6-6 解：6-7 解：（1）（2）6-8 解：6-9 解：6-10解：由于系统不稳定，因此系统误差为无穷大。

第二章2.1求下列函数的拉氏变换 （1）s s s s F 232)(23++=（2）4310)(2+-=s s s F （3）1)(!)(+-=n a s n s F （4）36)2(6)(2++=s s F（5） 22222)()(a s a s s F +-= （6）)14(21)(2s s s s F ++= （7）521)(+-=s s F 2.2 （1）由终值定理：10)(lim )(lim )(0===∞→∞→s t s sF t f f （2）11010)1(10)(+-=+=s s s s s F 由拉斯反变换：t e s F L t f ---==1010)]([)(1 所以 10)(lim =∞→t f t2.3（1）0)2()(lim )(lim )0(2=+===∞→→s ss sF t f f s t )0()0()()()](['2''0''f sf s F s dt e t f t f L st --==-+∞⎰)0()0()(lim )(lim'2''0f sf s F s dt e t f s st s --=+∞→-+∞+∞→⎰1)2()(lim )0(222'=+==+∞→s s s F s f s (2)2)2(1)(+=s s F , t te s F L t f 21)]([)(--==∴ ,0)0(2)(22'=-=--f te et f tt又，1)0('=∴f2.4解：dt e t f e t f L s F st s--⎰-==22)(11)]([)(⎰⎰------+-=2121021111dt e e dt e e sts sts)11(11)11(11222s s s s se s e s e e s s e -------+--=22)1(111s s e s e ---∙-=2.5求下列函数的拉氏反变换（1）t t f 2sin 21)(= （2）t e t t f -=361)(（3）t t e e t f 32321)(+-=- （4）t t e e t f 235352)(+=-（5）t e t e t f t t 3sin 313cos 2)(22--+= （6）t t t e e te t f 222)(----+-=2.6（1）0)()()(22=--dtt y d m t ky t f（2）0)()()(222121=-+-dt t y d m t y k k k k t f2.7（1）14312)(23++++=s s s s s G（2）210)(22++=-s s e s G s2.8 解 水的流量Q1由调节控制阀的开度控制，流出量Q2则根据需要可通过负载阀来改变，被调量H 反映了。