当前位置：文档之家 › 讲空间任意力系资料

讲空间任意力系资料

  • 格式：ppt
  • 大小：1.04 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

第五章 空间任意力系

第五章 空间任意力系
z B x
F
C β
α
y
A x1
y1
第五章 空间任意力系
例题6-2
§5–2 力对轴的矩
解： 1.力对轴AB的矩。
M ′ AB (F ) = M B (F )
z B x
例题 5-2 F
C β
α
y
F′
= − F cos β cos α ⋅ BC
= −3.18 N ⋅ m
应用解析式求解力对点B的矩。
M x (F ) = yFx − zFy
第五章 空间任意力系
例题6-1
§5–2 力对轴的矩
例题 5-1
由图示可以求出力F 解： 在各坐标轴上的投影和力 F 作用点C 的坐标分别 为：
Fx = F cos αcos β
Fy = F cos α sin β
Fz = F sin α
x= a = 4 m y= b = 6 m z= c =－3 m
2 2 2
力F 对原点O之矩方向余弦
cos( MO , i ) = Mx = 0.845 MO
cos( MO , j ) =
cos( MO , k ) =
My MO
= −0.531
Mz = 0.064 MO
第五章 空间任意力系
§5–2 力对轴的矩
例题 5-2
例5-2 在轴AB的手柄BC的一端作用着力F，试求这力对轴 AB以及对点B和点A的矩。已知AB=20 cm，BC=18 cm，F=50 N ，且α=45°，β=60°。
第五章 空间任意力系
§5–2 力对轴的矩
由
例题 5-1
M x (F ) = yFx − zFy
My (F ) = zFx − xFz

工程力学-第五章 空间任意力系

工程力学-第五章 空间任意力系
22
例题5
由题意有
Fr 0.36 Ft
解方程得
F 10.2 kN Fr 3.67 kN FAx 15.64 kN FAz 31.87 kN FBx 1.19 kN FBy 6.8 kN FBz 11.2 kN
2013-8-2 23
例题5
2. 取工件为研究对象，受力
z
M
0,
Fy r M O 0
11
例题2
水平传动轴上装有两个胶带轮C和D，半径分别是r1=0.4 m ， r2=0.2 m .
套在C 轮上的胶带是铅垂的，两边的拉力F1=3 400 N，F2=2 000 N，套在D轮 上的胶带与铅垂线成夹角α=30o，其拉力F3=2F4。求在传动轴匀速转动时，
3

2）力对轴之矩的计算
A：定义：
力Ｆ对任一z轴的
矩，等于这力在z
轴的垂直面上的投
影对该投影面和z
轴交点O的矩。
2013-8-2 4
R=Fi B：合力矩定理： MZ(R)=MZ(Fi ) 在直角弯的杆C 端作用 着力F，试求这力对坐 标轴的矩。已知:
OA=a=6 m，AB=b=4 m， BC=c=3 m， α=30º 60º ,β= 。
F
x
0,
FAx FBx ( F3 F4 ) sin 30 0
F
z
0,
FAz FBz ( F3 F4 ) cos 30 ( F1 F2 ) 0
M x 0, FAZ 0.25 m FBZ 1.25 m ( F3 F4 ) cos 30 0.75 m 0
例题4
某种汽车后桥半轴可看成支承在

空间任意力系

空间任意力系

FC
最大载重Pmax是多少。
Q FB
P
D
解: 取起重机为研究对象
A
B,C
My(F)0, FAaco3s0Qa3co3s0Pclos0
MC'x(F)0,
a FA2
FBaQa2P(a2lsin)0
y C
x’
Fz 0, FAFBFCPQ0
A
ED
x

解得: FA=19.3kN， FB=57.3kN， FC=43.4kN
d O1
O
MO MO cos MO MO sin
d MO MO sin
FR
FR
一般情形下空间任意力系可合成为力螺旋
(4) 空间任意力系平衡的情形
● F′R=0，MO=0
2019/11/15
原力系平衡
内容回顾
空间力系的简化与合成
主矢
主矩
最后结果
说
明
FR′ = 0
MO = 0 MO≠0
§5-5 空间任意力系的平衡条件及其应用
1、平衡条件及平衡方程：
平衡条件：
由平衡力系定理可知，空间一般力系平衡的充要条件：力 系的主矢和对任一点的主矩都等于零，即：
平衡方程：
FR Fi 0
M O M O i 0
由主矢与主矩的计算式，有
F R (F x F x i )0 2 i, (F F yy ) i2 i0 ,(F F zz i )i2 0
② 空间任意力系的平衡条件及其应用；
2019/11/15
§5-4 空间任意力系的简化
1. 空间力线平移定理
作用于刚体的力 F 可等效地平移到刚体上的任一点O， 但须附加一力偶，此附加力偶矩 矢M 等于原力对平移点O 的力矩矢MO（F）。

空间任意力系的简化)汇总

空间任意力系的简化)汇总
z
3cm 5cm
B
D

o x
y
A
P
9
解: 根据力对轴的矩的定义计算
作和x轴垂直的平面M1.
找出交点O. z 确定力P在平面 M1内的分力 Pyz=1.732 kN. o 在平面M1内确定 力Pyz到矩心O的距 x 离即力臂d1=8cm
5cm
B
3cm
D
d1 A
M1
y
Pyz P
计算力Pyz对点A的矩亦即力P对x轴的矩
z


A'
O'
C'
MD FR'
B'
最后简化结果为左螺旋.
o
D
A B
C
y
x
30
力对轴的矩
z
图示门，求力 F 对z
（矩轴）的矩。 将力分解：
F
O
d
Fz
A
F Z∥ z 轴 F xy ⊥z 轴
于是：Mz(F) = M
O(Fxy)
F xy
=Fxyd =2OA’B’面积
3
结论：力对轴的矩等于该力在垂直于此轴的平面上的分力
对此轴与这个平面交点的矩。
说明: （1）力对轴的矩是代数量。 正负号规定：右手螺旋法则。 （2）若力与轴空间垂直，则 无须分解。 （3）若 F // z 轴
所组成的空间力偶系可合成为一个力偶 , 其力
偶矩矢Mo称为原力系对简化中心的主矩. Mo = Mi = mo(Fi)
20
结论: 空间任意力系向任一点简化, 一般可得到
一个力和一个力偶. 这个力作用在简化中心, 它的 矢量称为原力系的主矢,并等于这力系中各力的矢 量和; 这个力偶的力偶矩矢等于原力系中各力对简 化中心的矩的矢量和,并称为原力系对简化中心的 主矩. 主矢FR'只取决于原力系中各力的大小和方向, 与简化中心的位置无关 ;而主矩 Mo 的大小和方向 都与简化中心的位置有关.

5 理论力学--空间任意力系

5 理论力学--空间任意力系
z FAz Mz
FAy My
y
x
Mx A FAx
图5-8
因此，按照空间任意力系简化理论，将固定端处 的约束力向固定端点A处简化，得到一个力和一个力 偶。 这个力的大小和方向不能确定，所以用三个正交 的分力来表示；这个力偶的大小和方向也不能确定， 也用三个正交的分量表示。
5.3 空间任意力系的平衡方程
A
Fy 0
列平衡方程
F F4 cos 0 F2 cos a F a 0
F3
y
x
O x MO
F2
y
主矢 的大小和方向余弦分别为
FR ( Fx ) 2 ( Fy ) 2 ( Fz ) 2
图5-5
, cos(FR , k )
cos( FR , i )
F
FR
x
, cos(FR , j )
F
FR
y
F
FR
z
空间力偶系可合成为一个力偶
5.3.1 空间任意力系的平衡方程 空间任意力系平衡的必要与充分条件为：力系的 主矢和对任意一点的主矩均等于零。
M O M O (F ) 0 FR F 0
空间任意力系的平衡方程
F 0 F 0 其中包含有三个投影方程和三个 F 0 力矩方程，共计6个独立方程，可 M (F ) 0 解6个未知量。 M (F ) 0 M (F ) 0
O
M (F ) ,k M
z O
结 论
空间任意力系向任一点简化后，一般得到一个 力和一个力偶 。 这个力作用于简化中心，其力矢等于原力系的主矢。 这个力偶的力偶矩矢等于原力系对简化中心的主矩。 空间任意力系的主矢与简化中心的位置无关，而 主矩一般随简化中心位置的改变而改变，与简化中心 的位置有关。

第四章 空间任意力系x

第四章 空间任意力系x
(4-4)
第一节 空间任意力系的简化
得到：
FRx Fix , FRy Fiy , FRz Fiz
（4-5）
而Ｆ的大小及方向余弦为：
2 2 2 FR FRx FRy FRz FRy FRx cos( FR , x) , cos( FR , y ) (4-6) FR FR FRz cos( FR , z ) FR
FR = F1 + F2 + + Fn = Fi
(4-1)
附加力偶系可合成为一个力偶，力偶矩ＭO等于各附 加力偶矩的矢量和，即MO=M１+M2+……+Mn，亦即等于 原力系中各力对于简化中心的矩的矢量和
M0 M01 M02 M0n M0i
(4-2)
矢量 FR = Fi称为原力系的主矢量，矢量 M 0 称为原力系对于简化中心Ｏ的主矩。
第一节 空间任意力系的简化
3、空间任意力系简化为一合力螺旋
若FR≠０，MO≠０，且MO 与FR 不相垂直，如图 （4-3a） ，则可用下述方法进一步简化。
图4-3
力 螺 旋
第一节 空间任意力系的简化
将MO 分解为垂直于FR 的M1 和平行于FR 的MR。
因M1 所代表的力偶与力 FR 位于同一平面V（⊥ M1）
即:
FR＝０，MO＝０
（4-15）
第二节 空间任意力系的平衡条件 平衡方程
过O点取直角坐标系Oxyz，上述条件可用代数方 程表示为：
F 0, F 0, F 0 M 0, M 0, M 0
ix iy iz ix iy iz
（4-16）
第二节 空间任意力系的平衡条件 平衡方程

第四章 任意力系1


F2 Fn
F1 M1
=
简化中心
M2 F2 Mn A
Fn
=
附加力偶
FR MA
r r F R = Σ Fi
FRx = ∑ Fix FRy = ∑ Fiy
FRX FRY cos α = , sin α = FR FR
主矩：MA=∑Mi= ∑MA（F i） 主矩： ∑
与简化中心A无关 无关， 与简化中心A有关 1、FR与简化中心 无关，MA与简化中心 有关 2、合力=主矢+主矩 合力=主矢+ 简化结果讨论： 简化结果讨论：
xC = r α ∫α
2 −
积分法
y dθ θ θ
x = 2 rcos θ 3
r
dS
1
α
2 1 2 2 rcos θ ( r )dθ = rsinα , 3 2 3α
x
如：α=π/2， 则:xc=(4r/3π) ，
例4-3：图示槽钢横截面，求：此截面重心的位置。 图示槽钢横截面， 此截面重心的位置。 =0， 解：取对称轴故yc=0，再分割成有规律的几个物体 xc=∑Ai xi/A ∑ A1=30•10=300cm2, x1=15cm； ； A2=20•10=200cm2, x2=5cm； ； A3=30•10=300cm2, x3=15cm； ；
'
r r 1、主矢 F =0 而主矩 M ≠0 合力偶 、 O R
简化结果讨论: 简化结果讨论:
与简化中心无关
r 2、 F ≠ 0 、 R
r MO = 0
合力
r r 3、 FR ≠ 0 ; M O ≠ 0 、 r r （1） F MO R
合力
F R
o
MO

理论力学空间任意力系


(M
zi
)2
cos(M , i) M x cos(M , j) M y cos(M , k) M z
M
M
M
平衡条件
空间力偶系平衡的充分必要条件是 :
M 0合力偶矩矢等于零
M ( M xi )2 ( M yi )2 (M zi )2
平衡方程
M ix M iy
0 0
M iz
M 2 M 2 sin
j M 2 cos
k
3 5
F
20.2
j
4 5
F
20.2k
合力偶矩矢 M M1 M 2 60i 12 j 16k
大小： M 602 122 162 63.25(N m)
（1）研究多个力偶的合成或力偶系的平衡，只要用力偶矩矢 进行运算即可；
（2）求合力偶矩矢时，一般只需求得其沿各坐标轴的分量即可。 也可进一步分析合力偶矩矢的大小及其方位角。
力与轴平行或与轴相交——即力与轴在同一平面内 时，力对该轴的矩为零。
Mz (F ) MO (Fxy) Fxy d M z (F) Mo (Fxy ) Fxy h
力对轴之矩等于力在该轴垂直面上的投影对该轴和 投影面的交点之矩
3、力对点之矩与力对过该点的轴之矩的关系
r
r
rrr
已知：力 F及r 力 F在三根坐标轴上的分力 ，Fx ，Fy， Fz
四、空间任意力系
1、空间任意力系向一点的简化
F1 F1 , F2 F2 , , Fn Fn M1 MO (F1), M2 MO (F2 ), , Mn MO (Fn )
n
FR F1 F2 F3 F1 F2 F3 Fi i 1 n
M O M1 M 2 M 3 M O F1 M O F2 M O F3 M O Fi

第5章 空间任意力系


四、空间力系的合力矩定理
定理的表述： 若空间一般力系有合力FR，则合力对作用面内任一点O（或任一轴x）的 矩，等于力系各力对同一点O （或同一轴x）之矩的矢量和（或代数和）。
MO (FR ) MO (Fi ) M x (FR ) M x (Fi )
——对点的合力矩定理
——对轴的合力矩定理
例： 水平传动轴上安装有带轮和 圆柱直齿轮。已知：带轮直径d1= 0.5m，其紧边与松边的拉力分别为 F1和F2，且有F1= 2F2，F2与水平线 夹角θ= 30 ° ；齿轮节圆直径 d2= 0.2 m，Ft=2kN, 啮合角α= 20°； 几何尺寸为：b = 0.2 m，c = e = 0.3 m；零件本身重量不计，设轴处于 平衡状态。求轴承A、B处的反力。 （Fr 与Ft 为齿轮的径向力和圆周力）
F
zi
0:
FA FB FC P 0
（3）
FA P FB FC 1.5 0.35 0.5 0.65kN
第五次作业：
5-1, 5-3(提示）, ５-５, ５-９
若坐标系原点为汇交力系交点O，则有：
(Fi ) 0, M y (Fi ) 0, M z (Fi ) 0
因而空间汇交力系的平衡充要条件或平衡方程为：
F
xi
0, Fyi 0, Fzi 0
三、平衡条件及平衡方程应用：
步骤： （1）选择适当的研究对象； （2）作受力分析，画出受力图； （3）选择适当的投影坐标轴和力矩轴（力矩轴与投影轴可不一致）； （4）列平衡方程，求解未知量。

O
M
主矩的方向： cos( M , x) O
M
x
(Fi ) M y (Fi ) M z (Fi )

空间任意力系


B
Fx
mz ( F ) mz ( Fx ) Fx a 25 2 50N .m
x
Fy a 2m
y
11
[练习1] 已知P=2000N, C点在Oxy平面内，求力P对三个 坐标轴的矩。
解：
Pz P sin 45 1000 2N
Pxy P cos45 1000 2 N Px Pxy sin 60 500 6 N Py Pxy cos60 500 2 N
mO ( F ) ( m x ( F )) 2 ( m y ( F )) 2 ( m z ( F )) 2
my (F ) mx ( F ) mz ( F ) cos ,cos ,cos mO ( F ) mO ( F ) mO ( F )
17
§5-3 空间汇交力系的合成与平衡
"
29
⑵ R '∥ M o ; 这种情况力与力偶不能再合成，这就是 力系简化的最终结果，称为力螺旋。如钻孔、攻丝、拧木
螺钉等。
力螺旋中力的作用线称为原力系的中心轴，中心轴过简 化中心。
O·
Mo R'
=
R' · O
O·
R'
Mo
=
· O
R'
右螺旋
左螺旋
力螺旋与力、力偶一样，都是组成力系的基本元素。
30
z
mo ( F )

F
B
r
A
x
O
b y
a Fxy
力对点的矩矢在过该点的任一轴上的投影等于力对该 轴的矩。
[mo (F )]z mz (F )
16
利用力对点之矩与对通过该点的轴之矩的关系计算力
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

MO
FR
MO d FR MO (FR ) MO (F)
合力矩定理：合力对某点之矩等于各分力对同一点之矩的矢 量和.
合力对某轴之矩等于各分力对同一轴之矩的代数和. （2）合力偶
当 FR 0,MO 0 时，最后结果为一个合力偶。此时与简化 中心无关。
（3）力螺旋
当 FR 0, MO 0, FR ∥MO 时
M AB F 0 M AE F 0
F6
a
a 2
P
0
F6
P 2
F5 0
M AC F 0
F4 0
MEF F 0
F6
a

a 2
P
F1
ab 0 a2 b2
MFG F 0
Fb
b 2
P
F2b
0
MBC F 0
F2
b
b 2
P
F3
cos
45
b
0
F1 0 F2 1.5P
F3 2 2P
Fr 0.36F , R 50mm, r 30mm
各尺寸如图
求： (1) Fr , F（2）A、B处约束力 （3）O 处约束力
解：研究对象1：主轴及工件，受力图如图
Fx 0
Fy 0
F FBx FAx Fx 0 FBy Fy 0
Fz 0
F FBz FAz Fz 0
MOy —偏航力矩
MOz —俯仰力矩
飞机向前飞行
飞机上升 飞机侧移 飞机绕x轴滚转 飞机转弯 飞机仰头
2． 空间任意力系的简化结果分析（最后结果） 1） 合力
当 FR 0, MO 0最后结果为一个合力.
合力作用点过简化中心.
当
FR 0, MO 0, FR MO
时，
d
MO FR
最后结果为一合力.合力作用线距简化中心为 d
第七讲 空间任意力系
湖南理工学院——曾纪杰
1． 空间任意力系向一点的简化
其中，各 Fi Fi ，各 Mi Mo(Fi )
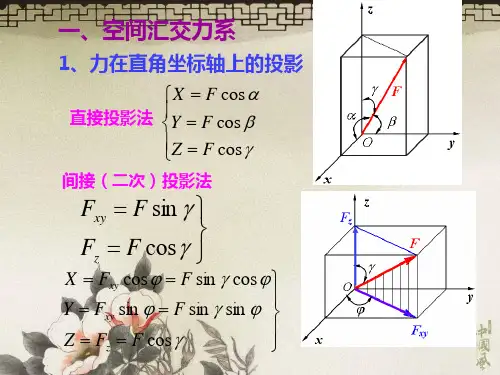
一空间汇交与空间力偶系等效代替一空间任意力系.
空间汇交力系的合力
FR Fi Fixi Fiy j Fixk
称为力系的主矢 空间力偶系的合力偶矩
Mo Mi Mo (Fi )
Fx 0 Fy 0 Fz 0 Mx 0 My 0 Mz 0
空间任意力系平衡的充要条件：所有各力在 三个坐标轴中每一个轴上的投影的代数和等 于零，以及这些力对于每一个坐标轴的矩的 代数和也等于零. 空间平行力系的平衡方程
Fz 0 Mx 0 My 0
2）.空间约束类型举例:表3-1
3）.空间力系平衡问题举例
力螺旋中心轴过简化中心
当 FR 0, MO 0, FR, MO 成角 , 且 FR, MO 既不平行也不垂直时
力螺旋中心轴距简化中心为
d MO sin
FR
（4）平衡
当 FR 0, MO 0时，空间力系为平衡力系
3 空间任意力系的平衡
空间任意力系平衡的充要条件：该力系的主矢、主矩分别为零. 1）.空间任意力系的平衡方程
称为空间力偶系的主矩 由力对点的矩与力对轴的矩的关系，有
Mo M x (F)i M y (F) j M z (F)k
式中，各分别表示各 Mx (F), M y (F), Mz (F)力
对 x，y，z ,轴的矩。
FRx —有效推进力 FRy —有效升力 FRz —侧向力
MOx —滚转力矩
例5： 已知：正方体上作用两个力偶
(F1, F1), (F2, F2),CD ∥ A2 E 不计正方体和直杆自重.
求：正方体平衡时， 力F1, F2 的关系和两根杆受力.
解：两杆为二力杆，取正方体，
Fz 0 F1 sin 30 F2 sin 60 FAx FBx 0 Fy 0 0 0
Fz 0 F1 cos 30 F2 cos 60 F FAz FBz 0
MxF 0
F1 cos30 200 F2 cos 60 200 F 200 FBz 400 0
M y F 0
M z F 0
F
R
D 2
F2
F1
0
F1 sin 30 200 F2 sin 60 200 FBx 400 0
结果： F1 3000N, F2 6000N, FAx 1004N, FAz 9397N,
FBx 3348N, FBz 1799N,
例3：
已知： Fx 4.25N, Fy 6.8N, Fz 17N,
例1：
已知： P=8kN, P1 10kN, 各尺寸如图
求：A、B、C 处约束力
解：研究对象：小车
受力：P, P1, FA, FB , FD ,
列平衡方程
Fz 0 P P1 FA FB FD 0
MxF 0 0.2P 1.2P1 2FD 0 M yF 0 0.8P1 0.6P 1.2FB 0.6FD 0
M z F 0 100Fx 30Fy M z 0
结果：FOx 4.25kN, FOy 6.8kN, FOz 17kN M x 1.7kNm, M y 0.51kNm, M z 0.22kNm
例4：
已知： F=2P及各尺寸 求： 杆内力
解：研究对象，长方板
受力图如图 列平衡方程
F 3.67kN, FAz 31.87kN, FBy 6.8kN, FBz 11.2kN,
研究对象2：工件受力图如图 列平衡方程
Fx 0 FOx Fx 0 Fy 0 FOy Fy 0
Fz 0 FOz Fz 0
M x F 0 100FZ M x 0 M y F 0 30FZ M y 0
MxF 0 488 76FBz 76F 388Fz 0
M y F 0
F R Fz r 0
Mz F 0 76F 488 76FBx 30Fy 388Fx 0
又： Fr 0.36F , 结果： F 10.2kN,
FAx 15.64kN,
FBx 1.19kN,
结果： FD 5.8kN, FB 7.777kN, FA 4.423kN
例2：
已知： F 2000N, F2 2F1, 30, 60, 各尺寸如图
求： F1, F2 及A、B处约束力 解：研究对象， 曲轴 受力：F, F1, F2, FAx , FAz , FBx , FBz
列平衡方程