理论力学(机械工业出版社)第三章空间力系习题解答

理论力学习题答案(总26页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 两点受力的构件都是二力杆。

( × ) 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 力的平行四边形法则只适用于刚体。

( × ) 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 只要物体平衡，都能应用加减平衡力系公理。

( × ) 凡是平衡力系，它的作用效果都等于零。

( × ) 合力总是比分力大。

( × ) 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × )若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ )当软绳受两个等值反向的压力时，可以平衡。

( × )静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ )静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )凡是两端用铰链连接的直杆都是二力杆。

( × )如图所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。

对非自由体的运动所预加的限制条件称为 约束 ；约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束力由 主动 力引起，且随 主动 力的改变而改变。

第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（）2．在理论力学中只研究力的外效应。

（）3．两端用光滑铰链连接的构件是二力构件。

（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。

则其合力可以表示为。

①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。

①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。

③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

3．三力平衡定理是。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。

①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。

5．在下述原理、法则、定理中，只适用于刚体的有。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

《理论力学》第三章作业参考答案习题3-9解：力F在x 、y 坐标轴上的投影分别为：)(03.169100050301010222N F x =⨯++=)(09.507100050301030222N F y =⨯++=力F作用点的坐标为1500.15x m m m =-=-，(10050)0.15y mm m =+=。

所以，0.15507.090.15169.09101.4(.)Z y x M xF yF N m =-=-⨯-⨯≈-答: 力F对z 轴的力矩为-101.4Nm .习题3-11解：力F在x 、y 、z 坐标轴上的投影分别为：00cos 60cos 304x F F F ==1cos 60sin 304y F F F=-=-FF F Z 2360sin 0-=-=力F的作用点C 的坐标为1sin 302o x r r==，cos 302o y r ==，z h =。

所以，()Fr h F h F r zF yF My z X341412323-=⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=()F r h F r F h xF zF Mz x y+=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=-=4323243rF F r F r yF xF Mxy Z214323412-=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=-=答：力F对x 、y 、z 轴的矩分别为：()134h r F -，)4h r F +，12rF-。

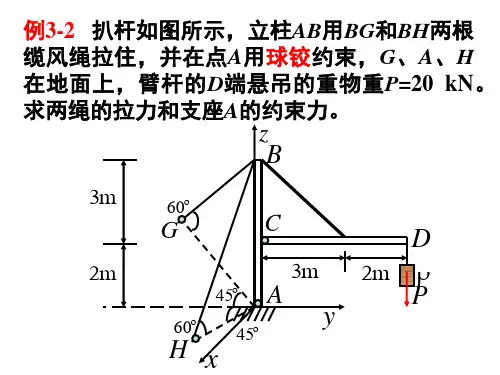
习题3-12解：以整个支架为研究对象。

由于各杆为二力杆，球铰链A 、B 、C 处的约束力A F 、B F 、C F 沿杆件连线汇交于D 端球铰链，与物块的重力P构成一空间汇交力系，其受力情况如图所示。

以O 为原点建立坐标系，列平衡方程，我们有⎪⎪⎩⎪⎪⎨⎧===∑∑∑000z y x F F F⎪⎩⎪⎨⎧=-++=++=-015sin 30sin 45sin 30sin 45sin 015cos 30cos 45sin 30cos 45sin 045cos 45cos 000000000000P F F F F F F F F C B A C B A B A 解之得：()()()cos1526.39()2sin 45sin 3015cos1526.39()2sin 45sin 3015cos 3033.46()sin 3015o A o o ooB o o ooC o o P F kN P F kN F P kN ⎧⎪==-⎪⎪⎪==⎨-⎪⎪⎪=-=-⎪-⎩答：铰链A 、B 的约束力均等于26.39kN ，方向与图示相同，即为压力，铰链C 的约束力等于-33.46 kN ，方向与图示相反，即为拉力。

第三章空间力系一、是非题1．一个力沿任一组坐标轴分解所得的分力的大小和这力在该坐标轴上的投影的大小相等。

（）2．在空间问题中，力对轴的矩是代数量，而对点的矩是矢量。

（）3．力对于一点的矩在一轴上投影等于该力对于该轴的矩。

（）4．一个空间力系向某点简化后，得主矢’、主矩o，若’与o平行，则此力系可进一步简化为一合力。

（）5．某一力偶系，若其力偶矩矢构成的多边形是封闭的，则该力偶系向一点简化时，主矢一定等于零，主矩也一定等于零。

（）6．某空间力系由两个力构成，此二力既不平行，又不相交，则该力系简化的最后结果必为力螺旋。

（）7．一空间力系，若各力的作用线不是通过固定点A，就是通过固定点B，则其独立的平衡方程只有5个。

（）8．一个空间力系，若各力作用线平行某一固定平面，则其独立的平衡方程最多有3个。

（）9．某力系在任意轴上的投影都等于零，则该力系一定是平衡力系。

（）10．空间汇交力系在任选的三个投影轴上的投影的代数和分别等于零，则该汇交力系一定成平衡。

（）二、选择题1．已知一正方体，各边长a，沿对角线BH作用一个力，则该力在X1轴上的投影为。

①0；②F/2；③F/6；④－F/3。

2．空间力偶矩是。

①代数量；②滑动矢量；③定位矢量；④自由矢量。

3．作用在刚体上仅有二力A、B，且A+B=0，则此刚体；作用在刚体上仅有二力偶，其力偶矩矢分别为M A、M B，且M A+M B=0，则此刚体。

①一定平衡；②一定不平衡；③平衡与否不能判断。

4．边长为a的立方框架上，沿对角线AB作用一力，其大小为P；沿CD边作用另一力，其大小为3P/3，此力系向O点简化的主矩大小为。

①6Pa；②3Pa；③6Pa/6；④3Pa/3。

5．图示空间平行力系，设力线平行于OZ轴，则此力系的相互独立的平衡方程为。

①Σmx（）=0，Σmy（）=0，Σmz（）=0；②ΣX=0，ΣY=0，和Σmx（）=0；③ΣZ=0，Σmx（F）=0，和Σm Y（）=0。

3-1 在边长为a 的正六面体上作用有三个力，如图 3-26所示，已知：F i =6kN, F 2=2kN, F 3=4kN 。

试求各力在三个坐标轴上的 投影。

图 3-26所示，已知六面体尺寸为 400 mmx 300 mmx300mm 正面有力F i =100N,中间有力F 2=200N,顶面有力偶 M=20N ・m作用。

试求各力及力偶对 z 轴之矩的和。

图 3-274 M z F 1 COS 450.40.3 20 J 34 20^2-240207.125 N m3-3如图3-28所示，水平轮上 A 点作用一力F =1kN,方向与 轮面成a=60°的角，且在过A 点与轮缘相切的铅垂面内，而点 A与轮心0的连线与通过0点平行于y 轴的直线成 b=45°角，图 3-28F COS sin 1000 COS 60 sin 45250^2 N 354 NF COS COS 1000 COS 60 sin 45250 (0 N 354 NF 1x 0F 1yF 2xF 2 COS 45讨仃 4 J 3F iz 72 kNF ,6 kNF 3X F ^y — kNF ayF 2yF COS 45734巧 F^ —— kN 33F 2—33kN3-2 如图 3-27 h =r=1m 。

试求力F 在三个坐标轴上的投影和对三个坐标轴之矩。

F xF z F sin 1000 sin 60 500 866 NM x (F) |F y | h |F z | 1 r cos 354 1866 1 cos 45258 N m M y (F) |F x | h |F z | r sin 354 1 866 1sin 45966 N mM z (F)F cosr1000 cos60 1500 N m主矩。

图 3-30F R xF 1 “2 屁200^5 100(14 821 .4NF R yF 2乐150714 561 .2NF RZF 1亦 F ?L 100V 5 50^14410.7NV 14F RJ ( 821.4)2( 2561.2)2410.71076.3N3-4 曲拐手柄如图3-29所示，已知作用于手柄上的力F =100N, AB=100mm BC=400mrm CC =200mrm a=30°。

第三章思考题解答3.1 答：确定一质点在空间中得位置需要3个独立变量，只要确定了不共线三点的位置刚体的位置也就确定了，故须九个独立变量，但刚体不变形，此三点中人二点的连线长度不变，即有三个约束方程，所以确定刚体的一般运动不需3n 个独立变量，有6个独立变量就够了.若刚体作定点转动，只要定出任一点相对定点的运动刚体的运动就确定了，只需3个独立变量；确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量，确定任一点在平面上的位置需二个独立变量，共需三个独立变量；知道了定轴转动刚体绕转动轴的转角，刚体的位置也就定了，只需一个独立变量；刚体的平动可用一个点的运动代表其运动，故需三个独立变量。

3.2 答物体上各质点所受重力的合力作用点即为物体的重心。

当物体的大小远小于地球的线度时物体上各质点所在点的重力加速度都相等，且方向彼此平行即重力场为均匀场，此时质心与重心重合。

事实上但物体的线度很大时各质点所在处g 的大小是严格相等，且各质点的重力都指向地心，不是彼此平行的，重心与质心不和。

3.3答 当物体为均质时，几何中心与质心重合；当物体的大小远小于地球的线度时，质心与重心重合；当物体为均质且大小远小于地球的线度时，三者都重合。

3.4 答 主矢F 是力系各力的矢量和，他完全取决于力系中各力的大小和方向，故主矢不随简化中心的位置而改变，故而也称之为力系的主矢；简化中心的位置不同，各力对简化中心的位矢i r 也就不同则各力对简化中心的力矩也就不同，故主矩随简化中心的位置而变，被称之为力系对简化中心的主矩。

分别取O 和O '为简化中心，第i 个力i F 对O 和O '的位矢分别为i r 和i r '，则i r =i r '+O O '，故()()iii ii i O F O O r F r M ⨯'-'=⨯'=∑∑'()∑∑⨯'-⨯'=ii ii i F O O F r ∑⨯'+=ii o F O O M即o o M M ≠'主矢不变，表明刚体的平动效应不变，主矩随简化中心的位置改变，表明力系的作用对刚体上不同点有不同的转动效应，但不改变整个刚体的转动规律或者说不影响刚体绕质心的转动。