网络图论及网络方程.共32页文档

电路-第9章网络图论基础

网络图论图论是数学的一个分支，是富有趣味和应用极为广泛的一门学科。

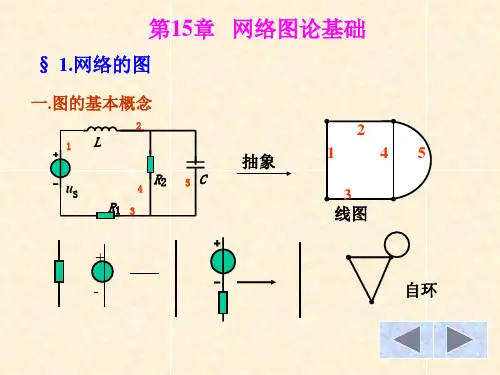
(1)图图(a)电路，如果用抽象线段表示支路则得到图(b)所示的拓扑图，它描述了电路的点和线的连接关系，称为电路的图。

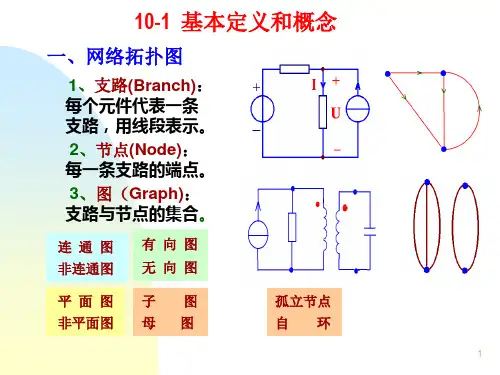
定义：图G 是描述电路结点支路连接关系的拓扑图，它是支路和结点的集合。

1）支路总是连接于两个结点上。

2）允许孤立结点存在，不允许孤立的支路存在。

移走支路，该支路连接的两个结点要保留在电路中，而移走结点，则要将连接于该结点的所有支路移走。

电路的图是用以表示电路几何结构的图形，图中的支路和结点与电路的支路和结点一一对应。

9.1 网络图论的基本概念(3)有向图：标示了参考方向的图(2)子图：图G1中的所有支路和结点都是图G中的支路和结点，则称G1是G 的一个子图。

子图示例9.1 网络图论的基本概念(4)连通图图中任何两结点之间存在由支路构成的路径，则称为连通图。

连通图和非连通图示例9.1 网络图论的基本概念(5)回路从某个结点出发，经过一些支路(一条支路仅经过一次)和一些结点(每个结点仅经过一次)又回到出发点所经闭合路径。

树和非树示例(6)树G1是G 的一个子图，且满足以下三个条件：A 、是连通的；B 、包含G 中所有结点；C 、不包含回路。

G1称为G 的一棵树。

9.1 网络图论的基本概念(7)树支、树支数构成树的支路称为树支。

树支数为：割集示例(8)连支、连支数不属于树的支路称为连支。

连支数为：(9)割集、割集方向移走某些支路，图分成了两个分离的部分，则这些支路的集合称为割集。

割集的方向：从一部分指向另一部分的方向。

9.2 关联矩阵、回路矩阵、割集矩阵、及KCL和KVL方程的矩阵形式(1)增广矩阵描述图中结点和支路关联情况的矩阵。

矩阵元素：增广矩阵为n×b 阶矩阵。

图9.2.1图的增广矩阵：9.2.1 关联矩阵A9.2 关联矩阵、回路矩阵、割集矩阵、及KCL 和KVL方程的矩阵形式(2)关联矩阵A增广矩阵每一列对应一条支路，非零元素两个，一个是1一个是-1，表示1号支路从1号结点流向2号结点；每一行代表一个结点，如第1行表示支路1、4、6连在1号结点，且支路1从1号结点流出，支路4流入1号结点，支路6流出1号结点。

图论与网络流理论ppt课件

1）V (G ) { v 1 ,v 2 , ,v }是非空有限集，称为顶点集，
2）E(G)是顶点集V(G)中的无序或有序的元素偶对 (vi,vj )
组成的集合，即称为边集,其中元素称为边.
图G的阶是指图的顶点数|V(G)|, 用v来表示；图的边的数
目|E(G)|用来表示.
用G (V (G )E ,(G )表)示图，简记 G(V,E).
算法。最短路问题有很多算法，其中最基本的一个是
Dijkstra算法
23
可编辑课件
3、Dijkstra算法
24
可编辑课件
25
可编辑课件
26
可编辑课件
27
可编辑课件
28
可编辑课件
定理 1.2.1 Dijkstra 算法结束时，对任一个顶点v，其标号l(v)恰是v0 到v 的最短路的长。
定理1.2.2 Dijkstra 算法的计算复杂度为O(υ 2 )。
9 图的同构
我们已经知道，同一个图可以有不同形状的图示。反过来，两个不同的图也可以有形状相同的图示。比如：
易见G1 和G2 的顶点及边之间都一一对应，且连接关
系完全相同，只是顶点和边的名称不同而已。这样的两个图称为是同构的(isomorphic)。
19
可编辑课件
定义1.1.1 对两个图G = (V(G),E(G))与H = (V (H),E(H))，
事实上，假如G 不连通，则至少有一个连通分支的顶点数不超过n。在此连通分支中，顶点的度至多是n −1。这与δ (G) ≥ n矛盾。证毕。例1.1.7 若图中只有两个奇度顶点，则它们必连通。
证明：用反证法。设u、v为仅有的两个奇度顶点。 18 假如u与v不连通，则它们必分属于不同的连通分支。将

图论与网络流理论

为判定两图同构，一般要按定义构造出两图顶点间的一一映射，然后检验它是否保持邻接关系。有时也可根据图的特点使用特殊方法。
1.2 最短路问题
1、赋权图对图G的每条边e，赋以一个实数w(e)，称为边e的权。
每个边都赋有权的图称为赋权图。权在不同的问题中会有不同的含义。例如交通网络
中，权可能表示运费、里程或道路的造价等。
解：Herschel 图的一个顶点二划分如下：可见 Herschel 图是一个二部图。
Peterson 图中含有奇圈，因此不是二部图。
8 连通性
图中两点的连通：如果在图G 中u，v 两点间有路相通，则称顶点u，v 在图G 中连通。
连通图（connected graph）：若图G 中任二顶点都连通，则称图G 是连通图。
1. 算法思想：先从图G 中找出权最小的一条边作为最小生成树的边，然后逐次从剩余边中选边添入最小生成树中，每次选边找出不与已选边构成圈的权最小的一条边。直至选出υ (G) −1条边为止。
(二)Prim算法（Robert Clay Prim，1957）
（三） Prim 算法的矩阵实现―求最小树的权矩阵法
事实上，假如G 不连通，则至少有一个连通分支的顶点数不超过n。在此连通分支中，顶点的度至多是n −1。这与δ (G) ≥ n矛盾。证毕。
例1.1.7 若图中只有两个奇度顶点，则它们必连通。
证明：用反证法。设u、v为仅有的两个奇度顶点。假如u与v
不连通，则它们必分属于不同的连通分支。将每个分支看成一个图时，其中只有一个奇度顶点。这与推论1.1.1 矛盾。证毕。
为边集的图称为G的补图，记为 G
定理1.1.1 对任何图G，其各顶点度数之和等于边数的2倍，
即 d(v) 2 vV (G)

图论基础知识汇总

图论基础知识汇总(总32页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除图与网络模型及方法§1 概论图论起源于18世纪。

第一篇图论论文是瑞士数学家欧拉于1736 年发表的“哥尼斯堡的七座桥”。

1847年，克希霍夫为了给出电网络方程而引进了“树”的概念。

1857年，凯莱在计数烷22 n n H C 的同分异构物时，也发现了“树”。

哈密尔顿于1859年提出“周游世界”游戏，用图论的术语，就是如何找出一个连通图中的生成圈，近几十年来，由于计算机技术和科学的飞速发展，大大地促进了图论研究和应用，图论的理论和方法已经渗透到物理、化学、通讯科学、建筑学、生物遗传学、心理学、经济学、社会学等学科中。

图论中所谓的“图”是指某类具体事物和这些事物之间的联系。

如果我们用点表示这些具体事物，用连接两点的线段（直的或曲的）表示两个事物的特定的联系，就得到了描述这个“图”的几何形象。

图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型，借助于图论的概念、理论和方法，可以对该模型求解。

哥尼斯堡七桥问题就是一个典型的例子。

在哥尼斯堡有七座桥将普莱格尔河中的两个岛及岛与河岸联结起来问题是要从这四块陆地中的任何一块开始通过每一座桥正好一次，再回到起点。

当然可以通过试验去尝试解决这个问题，但该城居民的任何尝试均未成功。

欧拉为了解决这个问题，采用了建立数学模型的方法。

他将每一块陆地用一个点来代替，将每一座桥用连接相应两点的一条线来代替，从而得到一个有四个“点”，七条“线”的“图”。

问题成为从任一点出发一笔画出七条线再回到起点。

欧拉考察了一般一笔画的结构特点，给出了一笔画的一个判定法则：这个图是连通的，且每个点都与偶数线相关联，将这个判定法则应用于七桥问题，得到了“不可能走通”的结果，不但彻底解决了这个问题，而且开创了图论研究的先河。

图与网络是运筹学（Operations Research ）中的一个经典和重要的分支，所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。

网络图论集网络方程

0 1 0 0 0
[Yb
]
0 0
0 0
3 0
0 2
0 0
0 0 0 0 1
0
0
0
0
[Us ] 0 [Is ] 0
1
0
0
1
Yn AYbAT
3 1 0
1 5 1
0 1 2
•
In
•
A Is AYb
•
Us
2 0
1
•
•
Yn Un In
1
4
2 35
12
七、含互感电路分析
Ib Bf T Il
•
•
•
[Bf ZbBf T ]Il [Bf Us Bf Zb Is ]
•
•
Zl Il Usl
1 1 0 1 0 0
[Bf
]
0
1 1 0 1 0
1 0 1 0 0 1
其中： Zl Bf ZbBf T
（回路阻抗矩阵）
•
•
•
Usl Bf Us Bf Zb Is
（回路电压源列向量）
(nxb) (bx1)
•
•
••
五、节点电压方程 (Ib Yb Ub Yb Us Is )
•
•
Y n
Un
In
(nxn) (nx1) (nx1)
u1 = un2 – un1
-i1u+2 =i4u–ni26 = 0 iu1 +3 =i2+uni23 –=un03
其中：1
[
A]
1
0
I•Y100n n10A1 I•As100YbA100AYbT10U•1s
1

网络图论和网络方程

L1:{4,5,6}
T2连:{2支,3,集5}1
L2:{1,4,6}
a a
b
4 5
3 c
T3树:{3余,4,5}
d b
L3:{1,2,6}
4 5
cT4树:{1余,5,4}
d L4:{2,3,6}
五、回路和基本回路
回路：从图中的某一个顶点出发，沿着边和顶点不重复地巡行一周回到原出发的顶点所得到的闭合路径称为回路。回路数用M表示。
1
a 3 b4 c
2
56
如 a3 b
i3 + u3 -
d
有向图G
(1) 图中各边的方向与所对应电路中各元件上的电
流方向一致；
(2)取各支路的电压与电流方向为关联方向。
3. 子图和补图实例
1
1
a 3 b4 c =a 3 b
2 56
2
c +b 4
c
G1和G2 的总和包括
5 6 了G 的全部
支路和节点。
(2) 连支：对一个图G 除去所选树的树支以外的每个
支路称为连支，用L支表示。
(3)树余(连支集)：与树互补的子图称为树余，又称
连支集，用L表示。
如
1
3 b4
a
a
c
2 56
2
b c
56
a 3b c
56
d
d
d
T1:{2,5,6}
T2:{3,5,6}
G
树支：T支为2,5和6 连支：L支为1,3和4
LT支支为为13,,25和和46
B1 {2,4,6} B2 {3,5,6}
B3 {1,4,5} B4 {2,3,4,5}

电路第十章网络图论及网络方程

8
1 0 0 0 0 -1 0 0 1 0 0
习题0 ：110-07 0求0Bf、1 C-1f -1 0 -1
1

[C
f
]

0 0 1 0 010 0树支0：10、21、30、05、19
-1 1
0 -1
0 0
1 0

0 0 0 0 1 0 0 0 0 1 -1
2、基本割集关联矩阵Cf
7
四、A、Bf、Cf关系
1 0 0 1 1 0
选一棵对树于，一支个路有编向号图，[A] 0 1 1 1 0 0
先树支后连支。则有： 0 0 1 0 1 1
A At Al
B Bt Bl Bt 1
1 1 0 1 0 0 [Bf ] 1 1 1 0 1 0
1 4
2 3
5
21
10-5 基本割集法
一、标准支路伏安关系

Ik Yk Uk Yk Usk Isk
二、矩阵形式支路伏安关系:

Ib Yb Ub Yb Us Is
其中： Yb : 支路导纳矩阵
三、支路电流关系:

Cf Ib 0
i1 - i4 + i6 = 0 i2 + i4 + i5 = 0
3
2、回路（Loop)
回路是连通图G的一个子图，满足：
1）连通图
2）每个节点仅关联两条支路
3）移去任一支路，则无闭合路径
基本回路：单连支回路，连支方向为回路方向。
3、割集（Cut) 割集是连通图G的一些支路的集合，满足： 1）移去该支路集合，则图恰好分成两部分；

电网络理论-第二章

T i B il Q i 0
2-25
QB i 0
T l
Q B
T f f
T
0 or
T t
B Q
0
T
0
T t
对同一有向图，任选一树，按先树枝后连枝顺序有：
Q B
B 1 Ql 1
Ql B
§2-3 图的基本矩阵形式
A与Qf 之间的关系对同一有向图，任选一树，按先树枝后连枝顺序写出矩阵：
2-26
A At Al B f Bt 1 Q 1 Q l f
§2-3 图的基本矩阵形式
结支 ② 1 -1 0 1 0 2 3 -1 1 0 -1 0 0 1 0 4 0 -1 1 0 5 0 0 1 -1
2-10
1 Aa= 2 3 4
6 ３４ 0 ６ ③ 1 ① ５ 0 ２ -1 ④ 1
降阶关联矩阵A
支路b
A=
结点 n-1
(n-1) b
§2-3 图的基本矩阵形式
矩阵形式的KVL：[ Qf ]T[ut ]=[u]
§2-3 图的基本矩阵形式注意连支电压可以用树支电压表示。 ut 1 T [u ] Qf ut T ut ul Ql ul QlT ut 小结
A KCL KVL B [B ] T [ il ] =[i] Q [Qf][i]=0
un1 un un2 un3
矩阵阵形式KVL
[u ] [ A] [un ]
T
§2-3 图的基本矩阵形式 2. 回路矩阵B
2-13
[B]=
独立回路
支路b
注意

第15章网络图论基础

ut 1 T Q[ u] = = [Q ] ut = T ut ul Ql
∴ ul = QlT ut 连支电压用树支电压表示
小结：小结： A KCL Ai=0 B BTil=i
T t l
Q Qi=0
B i = it
KVL ATu =u n Bu=0 ul= - Btut
it = −Ql il
QTut=u
ul = QlT ut
Ql = −BtT
§ 3. 节点法
一.节点方程的矩阵式节点方程的矩阵式电路分析依据：电路分析依据： KCL KVL
•
设标准支路为：设标准支路为：
.
IK Zk
•
•
I ek
ISk Uk
U SK
.
[A][ i ]=0 [u]=[A]T[un]
6 1 5 4 3 2
{2,4,5,6} 1 2 3
{2,3,6} 1 5 4 •
{1,3,5,6}是否割集？是否割集？是否割集 1 2 3 4 5 6 7 2 4 7
1 6
2
5 3
{1,2,3,4} 是否割集？是否割集？ 6 7 8
5
4 7 8
找割集方法：找割集方法：作封闭曲面 6 1 5 4 3 2 {1,3,5,6}为割集为割集 {2,3,6}为割集为割集 {2,4,5,6}为割集为割集连支集合不能构成割集基本割集 (单树支割集单树支割集) 单树支割集基本割集数=(n-1) 基本割集数
qij=
-1 0
４３２ 1
５
C1:{1,2,4} C2:{1,2,3,5} C3:{2,3,6} 支割集 4 C1 1 Q= C2 0 C3 0

1网络图论

A
C
• D
B
欧拉得出了一般结论，欧拉得出了一般结论，即存在单行曲线的必充分条件是奇次顶点奇次顶点（要、充分条件是奇次顶点（联接于顶点的线段数为奇数）的数目为0或。为奇数）的数目为或2。显然右图不满足此条件因此，七桥问题的答案是否定的。，因此，七桥问题的答案是否定的。在七桥问题中，欧拉用点表示陆地，在七桥问题中，欧拉用点表示陆地，用线段表示桥。图论中，表示桥。图论中，把一些事物及其之间的联系用点和连接于点与点之间的线段来表示，因此，点和连接于点与点之间的线段来表示，因此，图就是一些点与线段的集合。就是一些点与线段的集合。
m＝l＝b-(nt-1) =b-n。＝＝。
b＝nt ＝ 3。＝。 m＝l＝b-(nt-1) =1。＝＝。
增加虚线部分：增加虚线部分： b＝8 ， nt ＝ 7 。＝ m＝l＝b-(nt-1) =2。＝＝。
§1-3 割集
割集(cut set) ：割集
任一连通图G中符合下列两个条件的支路集任一连通图中，符合下列两个条件的支路集叫做图G的割集的割集。叫做图的割集。 (1) 该支路集中的所有支路被移去但所有节该支路集中的所有支路被移去(但所有节点予以保留)后原连通图留下的图形将是两个两个彼点予以保留后，原连通图留下的图形将是两个彼此分离而又各自连通的子图（含孤立节点）此分离而又各自连通的子图（含孤立节点）； (2) 该支路集中，当保留任一支路，而将其余该支路集中，当保留任一支路，的所有支路移去后，原连通图留下的图形仍然是连的所有支路移去后，原连通图留下的图形仍然是连通的。通的。
基本概念树支(tree branch)：树中的支路叫做树支。树支：树中的支路叫做树支。

图论与网络

h
b
x
c
w
Euler型定理
定理2 设G是连通圈，则G是Euler型的充要条件是G没有奇次数的顶点。
推论1 设G是一个连通图，则G有Euler链当且仅当G最多有两个奇数次数的顶点。
连通性
图G称为连通的，如果在G的任意两个顶点u 和v中存在一条(u,v)路。
两点顶点u和v等价当且仅当u和v中存在一条(u,v)路。不连通图至少有两个连通分支。 ω表示G的连通分支数。
网络规划概述
网络规划(Network Programming )是图论与线性规划的交叉学科，具有广泛的应用背景，比如，最短路问题、最小树问题、最大流问题、最优匹配问题等。
七桥问题
七桥问题图形
原理及方法
七桥问题是图论中的著名问题。1736年，Euler巧妙地将此问题化为图的不重复一笔画问题，并证明了该问题不存在肯定回答。原因在于该图形有顶点连接奇数条边。
M (G) 1 1 1 0 0 0 0 0 0 1 1 0 0 1
d (v2 ) 3
d (v3 ) 3
0 0 0 1 1 2 0 d (v4 ) 4
2 22 2 222
4+3+3+4=14=2×7
e1
v1
e2
v2
e5
e7
e3
e6
v4
e4
v3
关联矩阵性质
图G的关联矩阵M=(mij)为m×n矩阵；则每行元素之和等于相应顶点的度；每列元素之和等于2。
因此，图G的关联矩阵M所有元素之和既等于所有顶点的度之和，又等于边数的2倍。
定理设G是一个图，则
d(v) 2
vV (G)

第13章_网络的图网络矩阵与网络方程

u5 = −u1 − u2 + u3
(a′) (b′) (c′)
这说明：①连支电压可由树支电压线性组合得到。 ②树支电压不能由其它树支电压得到。结论：在全部支路电压中，树支电压是一组独立变量。
WangChengyou © Shandong University, Weihai
电路理论基础
第13章网络的图网络矩阵与网络方程
WangChengyou © Shandong University, Weihai
电路理论基础
第13章网络的图网络矩阵与网络方程
12
一个具有n个节点的网络，如果每对节点之间都有一条支路相连，则它的图形共有nn-2个树。
④ 4 3 ① 2 ② 1 (a) 6 ③ ① 2 ② 1 (b) 5 4 3 6 ④ 5 ③
l1 u 4 + u 2 − u3 = 0 l 2 u5 + u1 + u 2 −u 3 = 0 l3 u 6 + u 2 + u1 = 0
可由(a)与(b)相减得到
(a) (b) (c)
不再独立
结论：基本回路上列写的KVL方程是一组独立方程。独立方程的数目等于连支数。
WangChengyou © Shandong University, Weihai
WangChengyou © Shandong University, Weihai
电路理论基础
第13章网络的图网络矩阵与网络方程
8
割集定义中的要点是： ①移去割集后的图不连通； ②该不连通图具有两个分离部分（而不是多个）； ③割集是一个最小支路集合（少移去其中任意支路的图仍连通）。割集与非割集示例：
电路理论基础

《图论与网络流》课件

最ቤተ መጻሕፍቲ ባይዱ流最小割定理
总结词
最大流最小割定理是图论中一个重要的定理，它指出在一个有向图中，从源点到汇点的最大流等于最小割的容量。
详细描述
最大流最小割定理是解决网络流问题的重要理论依据，它提供了一种将最大流问题转化为最小割问题的思路。通过求解最小割问题，可以找到一个割点集合，使得从源点到汇点的流量等于该割的容量，从而得到最大流。在实际应用中，最大流最小割定理可以应
感谢您的观看
THANKS
02
图论中的基本问题
欧拉路径与欧拉回路
欧拉路径
一个路径是图中的一条边序列，使得每条边只经过一次，起点和
终点是同一点。
欧拉回路
一个路径是图中的一条边序列，使得每条边只经过一次，起点和终点是同一点，且所有节点均不重复。
总结
欧拉路径和回路是图论中的基本概念，它们在计算机科学、运筹学、电子工程等领域有广泛应用。
最小割算法
01
最小割算法是图论中求解最小割问题的算法，旨在将图划分为两个不相交的子集，使得两个子集之间的边权值之和最小。
02
最小割问题与最大流问题是互补的，一个问题的解可以通过另一个问题的解得到。
03
最小割算法的实现通常基于最大流算法，通过求解一系列最大流问题来逼近最小割问题的解。
04
最小割算法的时间复杂度也取决于所选的算法和图的具体结构，一般在多项式时间内可求解。
最小费用流算法
最小费用流问题考虑了流的代价，即每条边的容量和代价，要求在满足流量限制的前提下，总代价最小。
最小费用流算法的基本思想是通过不断优化流的路径和代价来逼近最小费用流的解。
最小费用流算法是图论中求解最小费用流问题的算法，旨在找到从源点到汇点具有最小费用的流。

08版电路基础第10章网络图论与网络方程

2、回路（Loop) 回路是连通图G的一个子图，满足： 1）连通图 2）每个节点仅关联两条支路 3）移去任一支路，则无闭合路径
2、回路（Loop) 回路是连通图G的一个子图，满足： 1）连通图 2）每个节点仅关联两条支路 3）移去任一支路，则无闭合路径
基本回路：单连支回路
基本回路的方向：单连支方向注：利用回路法求解电路时，可选基本回路作为独立回路
②
任意两个节点间至少有一条路经
图G1中所有的支路和节点都在图G中每个支路都表示该支路电流的方向
② ③ ① ④
①
③
④
② ③ ① ④
② ③
①
④

4、标准支路
Ik

Uk

4、标准支路

Ik

Uk

二、树、回路、割集 1、树（Tree): 连通图G的一个子图，满足： 1）含有G全部节点
2）连通图
二、回路关联矩阵B
1、回路关联矩阵B 行：代表回路序号列：代表支路序号矩阵元素取值:
1 0 0 1 1 0 0 1 0 0 1 1 B 0 0 1 1 0 1
1 2
1 ——同向关联：支路j与回路i关联,支路j方向与回路i方向一致。 ——反向关联：支路j与回路i关 bij 1 联,支路j方向与回路i方向相反。 0 ——无关联：支路j与回路i
第十章网络图论及网络方程
网络分析主要问题： 1）选择独立变量 ——拓扑学理论
2）列写网络方程 ——矩阵代数方程 3）网络方程求解 ——计算机应用
10-1 基本定义和概念
一、网络拓扑图
1、支路(Branch)：将每个元件用线段表示，每条线段称为支路。

第13章网络的图网络矩阵及网络方程

哥尼斯堡市区图
七桥问题的解决
用点表示陆地，用线表示陆地间的桥，便抽象成图。问题变成该图能否实现一笔画？
欧拉规则
A
(a)连接奇数个桥的陆地只有一
个或超过两个以上时，不能实
现一笔画。
B
D
(b) 连接奇数个桥的陆地仅有两个时，则从两者中任一陆地
出发，可以实现一笔画而停在
另一陆地。
C
(c) 每块陆地都连接有偶数个桥时，则从任一陆地出发都能
4
①
2
④
5
3 6
②1
支路：1 2 3 4 5 6 1 1 0 1 0 0 节点①
③
A'
0
1
1
0
0 1 节点②
1 0 0 0 1 1 节点③
0
0 1 1 1
0
节点④
除去节点④对－1 1 0 1 0 0
应的第4行
A＝ 0 －1 1 0 0 －1
1 0 0 0 －1 1
A' 的任意一行都可由其他n-1行来确定，它只有n-1个独
对于n个节点b条支路的图，定义一个矩阵(行号对应节点号，列号对应支路号),矩阵中第i行第j列元素定义为
1, 当支路 j从节点连i出；
aij
1，当支路 j向节点连i入；
0，当支路 j与节点 i不接直相连。
例如，对如图所示的电桥电路的图，其节点-支路关联矩A′为
13.1 网络的图树
基本要求：掌握网络的图、子图、连通图、割集和树等概念。
1. 网络的图
图(graph) :由“点” 和“线”组成。 • “点”也称为节点或顶点(vertex)，“线”也称为支路或

网络图论

电路理论
主讲骆建
第三章电路方程法（网络分析的一般方法）
（电路分析方法之二）
主讲
开课单位：电气与电子工程学院电工教学基地
骆建
1
2
第三章
网络分析的一般方法
3.1 网络图论的基本概念 3.2 有向图的矩阵表示
了解支路电流分析法重点掌握回路（电流）分析法重点掌握节点（电压）分析法
3.3 KCL与KVL方程的矩阵表示 3.4 支路电流分析法 3.5 节点电压分析法 3.6 回路电流分析法
6
支路j属于网孔i ，方向与i一致支路j属于网孔i ，方向与i相反支路j不属于网孔i
Bf = 1L F
(b-n+1) 单位矩阵树支对应的子矩阵
2、内网孔是一组独立回路
31 32
3-2-5 有向图矩阵间的关系 1.A与Bf（或M)的关系要求:各矩阵序号相同的列对应同一支路则： ABfT=0 支节 1 A= 2 3 或
支节 1 1 1 Aa= 2 -1 3 0 4 0
2 0 -1 1 0
3 0 0 1 -1 1 1 -1 0
4 -1 0 0 1 2 0 -1 1
5 0 1 0 -1 3 0 0 1
6 1 0 -1 0 4 -1 0 0 5 6 0 1 1 0 0 -1
Aa={aij}n b
节点数支路数
aij
Ub=AT Un
1 1 0 0 0 -1 -1 2 0 1 0 -1 -1 0 3 0 0 1 1 1 1
• 独立、完备的节点电压变量Un 。
39
u2 u4 0 u6 0 u1 = 0 u3 u5 和
6 Q3: { 1 , 5 ,3 , 6 }
4 保留4支路，图不连通的。

第1章网络图论与网络方程

第1章网络图论与网络方程§1.1 电路的线图电网络的两个基本定律是基尔霍夫电流定律（简称KCL ）和基尔霍夫电压定律（简称KVL ）。

对某一具体电网络，通常可以列出许多KCL 和KVL 方程。

但是所有这些方程并不都是独立的。

本节及下一节利用图论(graph theory)的有关概念和方法来解决如何列写独立的基尔霍夫定律方程问题。

图论是一门数学，研究由“点”和“线”构成的线图(linear graph) [简称图(graph)]。

基尔霍夫定律是网络结构对电流、电压的约束，与元件性质无关。

因此在列写基尔霍夫定律方程时，可以不用考虑元件，从而将电路抽象成由“点”和“线”组成的线图。

在本书中将“点”统称为节点，将“线”统称为支路(branch)。

1 元件的线图二端元件有一个独立的端子电流和一个端对电压，可用两个节点和一条支路来表示，如图1.1所示。

支路中的电流和两点间的电压分别称为支路电流和支路电压，并且电压电流取相同参考方向，称为关联参考方向，在支路上用一个箭头表示。

三端元件有3个端子电流和3个端对电压，如图1.2(a)。

电流电压分别受KCL 和KVL 约束，即0132312321=-+=+--u u u i i iu①(a)(b)iu , (a)(b)③③图1.1 二端元件的线图图1.2 三端元件的线图因此可以用两条支路和三个节点的线图来表示。

对图1.2(a)，取任意两个端子电流为独立电流变量，例如端子①和②的电流1i 、2i ，同时取这两个端子与端子③的电压1u 、2u 为独立的电压变量。

对应的线图如图1.2(b)所示。

依此类推，对n 端元件，如果存在m 个独立的端子电流或m 个独立的端对电压，则可抽象成m 条支路n 个节点的线图。

2 电路的线图有了元件的线图便可用以建立电路的线图。

图1.3是一示例。

将图(a)中的元件一一抽象成线图，再按照原来的关系联结起来，便得到图(b)所示的电路线图。

网络图论及网络方程.共32页文档

合集下载

电路-第9章网络图论基础

图论与网络流理论ppt课件

图论与网络流理论

图论基础知识汇总

网络图论集网络方程

网络图论和网络方程

电路第十章网络图论及网络方程

电网络理论-第二章

第15章网络图论基础

1网络图论

图论与网络

第13章_网络的图网络矩阵与网络方程

《图论与网络流》课件

08版电路基础第10章网络图论与网络方程

第13章网络的图网络矩阵及网络方程

网络图论

第1章网络图论与网络方程

文档推荐

最新文档

网络图论及网络方程.共32页文档

合集下载

电路-第9章 网络图论基础

图论与网络流理论ppt课件

图论与网络流理论

图论基础知识汇总

网络图论集网络方程

网络图论和网络方程

电路第十章 网络图论及网络方程

电网络理论-第二章

第15章 网络图论基础

1网络图论

图论与网络

第13章_网络的图 网络矩阵与网络方程

《图论与网络流》课件

08版电路基础第10章 网络图论与网络方程

第13章网络的图网络矩阵及网络方程

网络图论

第1章 网络图论与网络方程

文档推荐

最新文档

电路-第9章网络图论基础

电路第十章网络图论及网络方程

第15章网络图论基础

第13章_网络的图网络矩阵与网络方程

08版电路基础第10章网络图论与网络方程

第1章网络图论与网络方程