2019-2020学年高考数学一轮复习讲义 第11课时 函数的周期性 理.doc

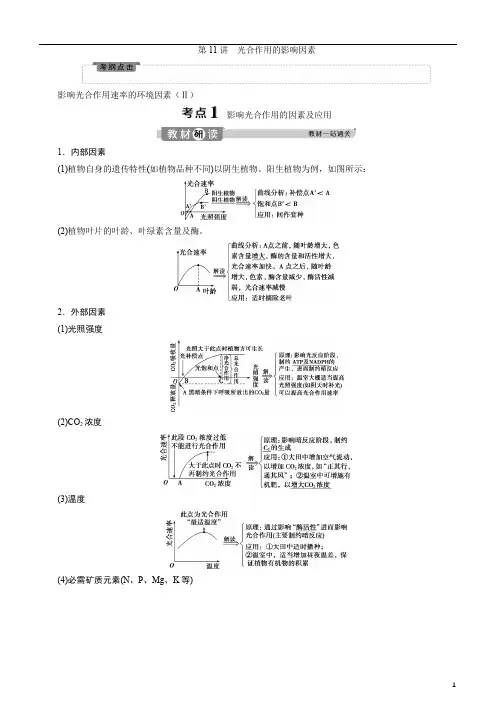
第11讲光合作用的影响因素影响光合作用速率的环境因素（Ⅱ）影响光合作用的因素及应用1．内部因素(1)植物自身的遗传特性(如植物品种不同)以阴生植物、阳生植物为例，如图所示：(2)植物叶片的叶龄、叶绿素含量及酶。

2．外部因素(1)光照强度(2)CO2浓度(3)温度(4)必需矿质元素(N、P、Mg、K等)据图分析多因素对光合作用的影响，回答下列问题：(1)三条曲线在P点之前限制光合速率的因素分别是________、__________、________。

(2)三条曲线在Q点之后横坐标所表示的因子________(填“是”或“不是”)影响光合速率的主要因素，此时的限制因素分别是________、__________、________。

(3)在北方的冬暖大棚中施用有机肥的益处包括____________________。

答案：(1)光照强度光照强度温度(2)不是温度CO2浓度光照强度(3)增加土壤肥力、增加大棚内的温度和CO2浓度考向1考查影响光合作用的环境因素1．(2019·湖北孝感一中等八所重点高中协作体联考)在CO2浓度为0.03%和适宜的恒定温度条件下，测定植物甲和植物乙在不同光照条件下的光合速率，结果如图。

下列有关分析正确的是()A．当光照强度为1 klx时，植物甲开始进行光合作用B．当光照强度为3 klx时，植物乙的总光合速率是0 mg/(100 cm2叶·h)C．若在c点时突然停止CO2供应，短时间内植物甲的叶绿体中C3的含量会增加D．d点时限制植物乙的光合速率增大的主要环境因素是CO2的浓度解析：选D。

光照强度为1 klx时，此时植物甲的光合作用强度等于呼吸作用强度，A错误；当光照强度为3 klx时，总光合速率＝净光合速率＋呼吸速率＝0＋20＝20 mg/(100 cm2叶·h)，B错误；c点的限制因素主要是CO2浓度，因此突然停止CO2供应，CO2固定受阻，短时间内C3的含量会减少，C错误；d点时植物乙到达光饱和点，因此光照强度不再是限制因素，而题中又提出此过程处于“适宜的恒定温度条件”，因此此时限制植物乙的光合速率增大的主要因素是CO2的浓度，D正确。

(1)函数f(x)=x3(x≥0)是奇函数.( × )
(2)若函数f(x)为奇函数,则必有f(0)=0.( × )
(3)若函数f(x),g(x)均为奇函数,则函数f(g(x))也为奇函数.( √ )
(4)若函数f(x)满足f(x-2)=f(x+3),则函数的周期为1.( × )
(5)若f(4+x)+f(4-x)=0,则函数y=f(4+x)是奇函数.( √ )
(方法2)作出函数f(x)的图象(图略),由f(x)的图象关于原点对称可知,函数为
奇函数.
方法总结判断函数奇偶性的常用方法
(1)定义法:
(2)图象法:
(3)性质法:
在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=
奇.
对点训练1(2021湖南岳阳高三模拟)设函数f(x)在(-∞,+∞)内有定义,下列函
故选B.
(2)解 ①函数定义域为R,且f(-x)=(-x)2-xsin(-x)=x2+xsin x=f(x),所以函数是
偶函数.
2
②函数定义域为 R,且 f(-x)=log2(-x+ (-) + 1)=log2(-x+√ 2 + 1)
=log2
1
+ 2 +1
=-log2(x+√ 2 + 1)=-f(x),所以函数是奇函数.
提示根据偶函数的定义,如果函数f(x+a)是偶函数,那么可得到
f(-x+a)=f(x+a),由此可得到函数f(x)图象的对称轴为直线x=a.也可从图象
变换的角度来理解,函数f(x+a)是偶函数,则其图象关于y轴对称,将该图象

函数的周期性一．知识点：1.周期函数的定义：对于函数f(x)，如果存在一个非零常数T，使得定义域内任何值f(x+T)=f(x)，那么就称f(x)为周期函数，T为f(x)的周期。

2.周期函数的性质：（1）若T（≠0）是f（x）的周期，则-T也是f（x）的周期。

（2）若T（≠0）是f（x）的周期，则nT（n为任意非零整数）也是f（x）的周期。

（3）若T1与T2都是f（x）的周期，则T1±T2也是f（x）的周期。

（4）若f（x）有最小正周期T*，那么f（x）的任何正周期T一定是T*的正整数倍。

（5）若T1、T2是f（x）的两个周期，且T1/T2是无理数，则f（x）不存在最小正周期。

（6）周期函数f（x）的定义域M必定是至少一方无界的集合3.判定定理：定理1. 若f（x）是在数集M上以T*为最小正周期的周期函数，则K f（x）+C（K≠0）和1/ f（x）分别是集M和集{X/ f（x）≠0，X ∈M}上的以T*为最小正周期的周期函数。

定理2. 若f（x）是集M上以T*为最小正周期的周期函数，则f（ax+b）是集{x|ax+b∈M}上的以T/ a为最小正周期的周期函数，（其中a、b为常数）。

定理3. 设f（u）是定义在集M上的函数，u=g（x）是集M1上的周期函数，且当X∈M1时，g（x）∈M，则复合函数f（g（x））是M1上的周期函数。

定理4. 设f1（x）、f2（x）都是集合M上的周期函数，T1、T2分别是它们的周期，若T1/T2∈Q则它们的和差与积也是M上的周期函数，T1与T2的公倍数为它们的周期。

4.几个常见常考周期函数的关系式：（其中a≠0）（1）f(x+a)= -f(x) =>f(x+2a)=f(x)（2）f(x+a)=1/f(x) =>f(x+2a)=f(x)（3）f(x+a)= -1/f(x) =>f(x+2a)=f(x)（4）若奇函数f(x)的图像关于直线x=a对称，则f(x+4a)=f(x)（5）若偶函数f(x)的图像关于直线x=a对称，则f(x+2a)=f(x)二．典型例题（难）：例题1：已知定义在R上的奇函数f(x)的图像关于直线x=1对称，则f(1)+f(2)+…+f(2019)=_______例题2：已知定义在R上的函数f(x)满足f(x+2)=12f(x)且当x∈[0,2]时，f(x)= -2sinπ2x①若当x∈[ -4,-2]时，f(x)≥t➖9t恒成立，则t的取值范围为________②函数g(x)=f(x) ➖12log16X 零点的个数为________例题答案：例题一：0 例题二：t≤9或0＜t≤1 ； 5三．基础例题1.若函数f（x）=x2+bx+c对一切实数都有f（x+2）=f（2 -x）则有（）A．f（2）＜f（1）＜f（4）B．f（1）＜f（2）＜f（4）C．f（2）＜f（4）＜f（1）D．f（4）＜f（2）＜f（1）2.已知定义在R上的函数f（x）满足f（-x）= - f（x），f（3-x）=f(x)，则f（2019）=（）A．- 3 B.0 C.1 D.33.已知定义在R上的函数f（x）满足：y=f（x - 1）的图像关于点（1，0）对称，且当0≥0时恒有f（x）=f（x+2），当x∈[0,1]时，f（x）=ex – 1，则f（2016）+f（-2015）=（）A．1 – e B. e – 1 C. – 1 – e D.e+14.定义在R上奇函数f（x）满足f（x+2）= -f（x），且在[0，2）上单调递减，则下列结论正确的是（）A．0＜f（1）＜f（3） B. f（3）＜0＜f（1）C．f（1）＜0＜f（3） D. f（3）＜f（1）＜05.已知函数f（x）的图像关于点（- 3 ，2 ）对称，则函数h（x）=f（x+1）- 3的图像的对称中心是_______6.设f（x）是定义在R上的奇函数，且在( -∞，0 )上是减函数，f（-2）=0，则xf（x）＜0的解集为________7.已知f（x）,g（x）都是定义在R上的函数，且f（x）为奇函数，g（x）的图像关于直线x=1对称，则下列四个结论中错误的是（）A．y=g[f(x)+1]为偶函数 B.y=g[f(x)]为奇函数C.函数y=f[g(x)]的图像关于直线x=1对称D．y=f[g(x+1)]为偶函数8.定义在R上得函数f(x)满足f( - x)=f(x),且当x≥0时，f(x)={−x2+1，0≤x≤12−2x，x≥1若对任意得x∈[m,m+1]，不等式f（1-x）≤f（x+m）恒成立，则实数m的最大值是（）A．- 1 B.12C. - 13D.13答案：1. A由已知得：对称轴为x=2，由于抛物线开口向上，所以越靠近对称轴值越小2.B∵f（- x）= - f（x）,∴f（3 - x）= - f（x - 3），且f（0）=0.又∵f（3 - x）=f（x），∴f（x）= - f（x - 3），∵f（x - 3）= - f（x - 6）,∴f（x）=f（x - 6），∴f（x）是周期为6的函数，∴f（2019）=f（6×336+3）=f（3）=（0）=03.A∵y=f（x - 1）的图像关于点（1，0）对称，∴f（x）的图像关于远点对称，∵当x≥0时恒有f（x）=f（x+2），∴函数f（x）的周期为2∴f（2016）+f（- 2015）=f（0）- f（1）=1 – e4.C由函数f（x）时定义在R上的奇函数，得f（0）=0，由f（x+2）= - f（x），得f（x+4）= - f （x+2）=f（x），故函数f（x）是以4为周期的周期函数∴f（3）=f（- 1）又∵f（x）在[0,2）上单调递减，∴函数f（x）在（- 2，2 ）上单调递减∴f（-1）＞f（0）＞f（1）5.（- 4，- 1）函数h（x）=f（x+1）- 3的图象是由函数f（x）的图像向左平移1个单位，再向下平移1个单位，再向下平移3个单位得到的，又f（x）的图像关于点（- 3，2）对称，所以函数h（x）的图像的对称中心为（-4，-1）6．(-∞，-2]∪[0，2]（1）x=0时，xf（x）=0，满足要求；（2）x＜0时xf（x）≤0，所以，f（x）≥0f（x）在（-∞，0）上是减函数，f（-2）=0所以，x≤-2（3）x＞0时，xf（x）≤0，所以，f（x）≤0f（x）为R上的奇函数，且在（-∞，0）上是减函数，所以在（0，+∞）上是减函数，f（2）=0f（x）≤0，解得，0＜x≤2所以，不等式 xf（x）≤0 的解集为(-∞，-2]∪[0，2]7. B已知得f （- x ）= - f （x ），g （1 - x ）=g （1+x ）， ∵g[f(-x)+1]=g[ - f(x)+1]=g[f(x)+1]，∴y=g[f(x)+1]为偶函数∵f[g(x)]=f[g(2 - x)]∴y=f[g(x)]得图像关于直线x=1对称∵f[g( - x+1)]=f[g(x+1)]∴y=f[g(x+1)]为偶函数∵g[f( - x)]=g[ - f(x)]=g[2+f(x)]∴y=g[f(x)]不是基函数8. C由题知函数f(x)为偶函数，且当x ≥0时，函数f(x)为减函数，则当x ＜0时，函数f （x ）为增函数。

第11章 算法复数推理与证明 第2讲A 组 基础关1．(2018·榆林模拟)已知复数z 1＝6－8i ，z 2＝－i ，则z 1z 2＝( ) A ．8－6i B ．8＋6i C ．－8＋6i D ．－8－6i 答案 B解析 z 1z 2＝6－8i －i＝(6－8i)·i＝8＋6i.2．(2019·青岛模拟)在复平面内，复数z ＝4－7i2＋3i (i 是虚数单位)，则z 的共轭复数z 在复平面内对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案 B 解析 z ＝4－7i2＋3i＝4－7i2－3i13＝－13－26i 13＝－1－2i ，其共轭复数z ＝－1＋2i对应的点(－1,2)在第二象限．3．(2018·河南省天一大联考)已知复数z ＝2－3i ，若z 是复数z 的共轭复数，则z ·(z ＋1)＝( )A ．15－3iB ．15＋3iC ．－15＋3iD ．－15－3i答案 A解析 依题意，z ·(z ＋1)＝(2－3i)(3＋3i)＝6＋6i －9i ＋9＝15－3i.4．(2019·广东测试)若z ＝(a －2)＋a i 为纯虚数，其中a ∈R ，则a ＋i 71＋a i＝( )A ．iB ．1C ．－iD ．－1 答案 C解析 ∵z 为纯虚数，∴⎩⎨⎧a －2＝0，a ≠0，∴a ＝2，∴a ＋i 71＋a i ＝2－i 1＋2i ＝2－i 1－2i 1＋2i1－2i＝－3i3＝－i.故选C.5．已知m 为实数，i 为虚数单位，若m ＋(m 2－4)i>0，则m ＋2i2－2i＝( )A ．iB ．1C ．－iD ．－1 答案 A解析 因为m ＋(m 2－4)i>0，所以m ＋(m 2－4)i 是实数，所以⎩⎨⎧m >0，m 2－4＝0，故m ＝2.所以m ＋2i 2－2i＝2＋2i 2－2i ＝1＋i1－i＝i. 6．(2018·成都市第二次诊断性检测)若虚数(x －2)＋y i(x ，y ∈R )的模为3，则yx的最大值是( )A.32B.33C.12 D.3 答案 D解析 因为(x －2)＋y i 是虚数， 所以y ≠0，又因为|(x －2)＋y i|＝3， 所以(x －2)2＋y 2＝3.因为y x是复数x ＋y i 对应点的斜率，所以⎝ ⎛⎭⎪⎫y x max ＝tan ∠AOB ＝3，所以y x 的最大值为 3.7．(2017·全国卷Ⅰ)设有下面四个命题：p 1：若复数z 满足1z ∈R ，则z ∈R ；p 2：若复数z 满足z 2∈R ，则z ∈R ； p 3：若复数z 1，z 2满足z 1z 2∈R ，则z 1＝z 2； p 4：若复数z ∈R ，则z ∈R .其中的真命题为( )A ．p 1，p 3B ．p 1，p 4C ．p 2，p 3D ．p 2，p 4 答案 B解析 设z ＝a ＋b i(a ，b ∈R )，z 1＝a 1＋b 1i(a 1，b 1∈R )，z 2＝a 2＋b 2i(a 2，b 2∈R )． 对于p 1，若1z ∈R ，即1a ＋b i ＝a －b ia 2＋b 2∈R ，则b ＝0且a ≠0⇒z ＝a ＋b i ＝a ∈R ，所以p 1为真命题．对于p 2，若z 2∈R ，即(a ＋b i)2＝a 2＋2ab i －b 2∈R ，则ab ＝0.当a ＝0，b ≠0时，z ＝a ＋b i ＝b i ∈/ R ，所以p 2为假命题．对于p 3，若z 1z 2∈R ，即(a 1＋b 1i)(a 2＋b 2i)＝(a 1a 2－b 1b 2)＋(a 1b 2＋a 2b 1)i ∈R ，则a 1b 2＋a 2b 1＝0.而z 1＝z 2，即a 1＋b 1i ＝a 2－b 2i ⇔a 1＝a 2，b 1＝－b 2.因为a 1b 2＋a 2b 1＝0⇒/a 1＝a 2，b 1＝－b 2，所以p 3为假命题．对于p 4，若z ∈R ，即a ＋b i ∈R ，则b ＝0⇒z ＝a －b i ＝a ∈R ，所以p 4为真命题．故选B.8．(2017·天津高考)已知a ∈R ，i 为虚数单位，若a －i2＋i为实数，则a 的值为________．答案 －2解析 ∵a ∈R ，a －i2＋i＝a －i2－i 2＋i 2－i ＝2a －1－a ＋2i 5＝2a －15－a ＋25i 为实数，∴－a ＋25＝0，∴a ＝－2.9．(2018·合肥模拟)设z 2＝z 1－i z 1(其中z 1表示z 1的共轭复数)，已知z 2的实部是－1，则z 2的虚部为________．答案 1解析 设z 1＝a ＋b i ，z 2＝－1＋c i ， 因为z 2＝z 1－i z 1，所以－1＋c i ＝(a ＋b i)－i(a －b i)＝(a －b )＋(b －a )i ，所以⎩⎨⎧a －b ＝－1，b －a ＝c ，所以c ＝1，所以z 2的虚部为1.10．已知复数z ＝i ＋i 2＋i 3＋…＋i 20221＋i ，则复数z 在复平面内对应点的坐标为________．答案 (0,1)解析 因为i 4n ＋1＋i 4n ＋2＋i 4n ＋3＋i 4n ＋4＝i ＋i 2＋i 3＋i 4＝0， 而2022＝4×505＋2，所以z ＝i ＋i 2＋i 3＋…＋i 20221＋i ＝i ＋i 21＋i ＝－1＋i1＋i＝－1＋i1－i 1＋i1－i ＝2i2＝i ，对应的点为(0,1)．B 组 能力关1．(2018·华南师大附中模拟)欧拉公式e i x ＝cos x ＋isin x (i 为虚数单位)是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，已知e a i 为纯虚数，则复数sin2a ＋i1＋i在复平面内对应的点位于( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限答案 A解析 由题意得e a i＝cos a ＋isin a 是纯虚数，所以⎩⎨⎧cos a ＝0，sin a ≠0，所以sin2a ＝2sin a cos a ＝0，sin2a ＋i 1＋i ＝i 1＋i ＝i 1－i 2＝1＋i 2，其在复平面内对应的点⎝ ⎛⎭⎪⎫12，12在第一象限． 2．对于复数z 1，z 2，若(z 1－i)z 2＝1，则称z 1是z 2的“错位共轭”复数，则复数32－12i的“错位共轭”复数为( )A ．－36－12iB ．－32＋32iC.36＋12i D.32＋32i 答案 D解析 由(z －i)⎝ ⎛⎭⎪⎫32－12i ＝1，可得z －i ＝132－12i ＝32＋12i ，所以z ＝32＋32i.故选D.3．(2019·西安模拟)已知方程x 2＋(4＋i)x ＋4＋a i ＝0(a ∈R )有实根b ，且z ＝a ＋b i ，则复数z 等于( )A ．2－2iB ．2＋2iC ．－2＋2iD ．－2－2i答案 A解析 由题意得b 2＋(4＋i)b ＋4＋a i ＝0， 整理得(b 2＋4b ＋4)＋(a ＋b )i ＝0，所以⎩⎨⎧ b ＋22＝0，a ＋b ＝0，所以⎩⎨⎧a ＝2，b ＝－2，所以z ＝2－2i.4．已知复数z 在复平面内对应的点在第三象限，则z 1＝z ＋|z |在复平面内对应的点在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案 A解析 令z ＝a ＋b i(a <0，b <0)，则|z |＝a 2＋b 2>|a |，z 1＝z ＋|z |＝(a 2＋b 2＋a )－b i ，又a 2＋b 2＋a >0，－b >0，所以z 1在复平面内对应的点在第一象限．5．已知复数z ＝(a －2)＋(a ＋1)i(a ∈R )的对应点在复平面的第二象限，则|1＋a i|的取值范围是________．答案 [1，5)解析 复数z ＝(a －2)＋(a ＋1)i 对应的点的坐标为(a －2，a ＋1)，因为该点位于第二象限，所以⎩⎨⎧a －2<0，a ＋1>0，解得－1<a <2.所以|1＋a i|＝1＋a 2∈[1，5)．6．复数z 1，z 2满足z 1＝m ＋(4－m 2)i ，z 2＝2cos θ＋(λ＋3sin θ)i(m ，λ，θ∈R )，并且z 1＝z 2，则λ的取值范围是________．答案 ⎣⎢⎡⎦⎥⎤－916，7解析 由复数相等的充要条件，可得⎩⎨⎧m ＝2cos θ，4－m 2＝λ＋3sin θ，化简得4－4cos 2θ＝λ＋3sin θ，由此可得λ＝－4cos 2θ－3sin θ＋4＝－4(1－sin 2θ)－3sin θ＋4＝4sin 2θ－3sin θ＝4⎝ ⎛⎭⎪⎫sin θ－382－916，因为sin θ∈[－1,1]，所以λ∈⎣⎢⎡⎦⎥⎤－916，7.。

03 考场 ·笑傲全国题
一、选择题
1.(2019·眉山)函数y= xx−+12中自变量x的取值范围是( A)
A.x≥-2且x≠1 B.x≥-2 C.x≠1 D.-2≤x＜1
2.(2019·海南)如图，在平面直角坐标系中，已知点A(2，1)，点B(3，-1)，
平移线段AB，使点A落在点A1(-2，2)处，则点B的对应点B1的坐标为( C )
乙车到B地时，甲车距B地的距离为120-100＝20(千米)，
乙车返回与甲相遇时间为20÷(120+100)=111 (时)， 因此甲、乙两车第二次相遇时甲行驶的时间是3+111=3141. 故选A.
变式训练
5.(2018·重庆模拟)今年“五一”节，小明外出爬山，他从山脚爬到山顶的过 程中，中途休息了一段时间，设他从山脚出发后所用的时间为t(分钟)，所走
变式训练
3.(2018·重庆模拟)函数y=
x 中x的取值范.x≥-2且x≠0
B.x＞-2且x≠0
C.x＞-2
D.x≠0
4.(2018·重庆模拟)下列各曲线中表示y是x的函数的是( D )
焦点3 实际问题与函数图象的关系
样题3 甲、乙两车分别从A地、C地同时向B地匀速行驶(C在A、B两地之
A.(-1，-1) B.(1，0) C.(-1，0) D.(3，0)
3.(2019·随州)第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很 不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌 龟先跑一段距离我再去追都可以赢．结果兔子又一次输掉了比赛，则下列
函数图象可以体现这次比赛过程的是( B )
5.(2019·日 照 ) 如 图 ， 在 单 位 为 1 的 方 格 纸 上 ， △ A1A2A3 ， △ A3A4A5 ， △A5A6A7，…，都是斜边在x轴上，斜边长分别为2，4，6，…的等腰直角 三角形，若△A1A2A3的顶点坐标分别为A1(2，0)，A2(1，1)，A3(0，0)，则

【解析】 (1)由图象可求得一次函数的解析式为 y＝30x－570，令 30x－570 ＝0，解得 x＝19. (2)设每个售价定为 x 元，则利润 y＝(x－80)·[400－(x－90)·20]＝－20[(x－ 95)2－225]． 所以当 x＝95 时，y 最大． 【答案】 (1)19 (2)95
利用函数图象刻画实际问题
(师生共研)
(2020·高考北京卷)为满足人民对美好
生活的向往，环保部门要求相关企业加强污
水治理，排放未达标的企业要限期整改．设
企业的污水排放量 W 与时间 t 的系为 W＝f(t)，用－f（b）b－ －fa（a）的大小评价在a，b这段时间内企业污水治理能
力的强弱．已知整改期内，甲、乙两企业的污水排放量与时间的关系如图
【解析】 (1)设老师上课时声音强度，一般两人小声交谈时声音强度分别 为 x1 W/m2，x2 W/m2， 根据题意得 d(x1)＝9lg1×x110－13＝63， 解得 x1＝10－6， d(x2)＝9lg1×x120－13＝54， 解得 x2＝10－7，所以xx12＝10， 所以老师上课时声音强度约为一般两人小声交谈时声音强度的 10 倍，故选 B．
√A．10 %
C．50 %
B．30 % D．100 %
解析：将信噪比NS从 1000 提升至 2000，C 大约增加了
Wlog2（1＋2 000）－Wlog2（1＋1 000） Wlog2（1＋1 000）
＝log22
001－log21 log21 001
001≈10.9697.9－679.967≈10%，故选
A．2 023 年
B．2 024 年
√C．2 025 年
D．2 026 年
【解析】 根据题意，知每年投入的研发资金增长的百分率相同，所以， 从 2 021 年起，每年投入的研发资金组成一个等比数列{an}，其中，首项 a1 ＝130，公比 q＝1＋12%＝1.12，所以 an＝130×1.12n－1.由 130×1.12n－1>200， 两边同时取对数，得 n－1>lg l2g－1l.1g21.3，又lg l2g－1l.1g21.3≈0.300－.050.11＝3.8， 则 n>4.8，即 a5 开始超过 200，所以 2 025 年投入的研发资金开始超过 200 万元，故选 C．

函数的周期专题六性1．周期函数的定义对于函数y ＝f (x )，如果存在一个非零常数T ，使得当x 取定义域内的任何值时，都有f (x ＋T )＝f (x )，那么就称函数y ＝f (x )为周期函数，称T 为这个函数的周期．如果T 是函数y ＝f (x )的周期，则kT (k ∈Z 且k ≠0)也是y ＝f (x )的周期，即f (x ＋kT )＝f (x )；如果在周期函数f (x )的所有周期中存在一个最小的正数，那么这个最小正数就叫做f (x )的最小正周期．2．函数周期性常用的结论结论1：若f (x ＋a )＝f (x －a )，则f (x )的一个周期为2a ；结论2：若f (x ＋a )＝－f (x )，则f (x )的一个周期为2a ；结论3：若f (x ＋a )＋f (x )＝c (a ≠0)，则f (x )的一个周期为2a ；结论4：若f (x )＝f (x ＋a )＋f (x －a )(a ≠0)，则f (x )的一个周期为6a ；结论5：若f (x ＋a )＝1f (x )，则f (x )的一个周期为2a ；结论6：若f (x ＋a )＝－1f (x )，则f (x )的一个周期为2a ；结论7：若函数f (x )关于直线x ＝a 与x ＝b 对称，则f (x )的一个周期为2|b －a |．结论8：若函数f (x )关于点(a ，0)对称，又关于点(b ，0)对称，则f (x )的一个周期为2|b －a |．结论9：若函数f (x )关于直线x ＝a 对称，又关于点(b ，0)对称，则f (x )的一个周期为4|b －a |．结论7—结论9的记忆：两次对称成周期，两轴两心二倍差，一轴一心四倍差．总规律：在函数的奇偶性、对称性、周期性中，知二断一．即这三条性质中，只要已知两条，则第三条一定成立．考点一已知函数的周期性(显性的)，求函数值【方法总结】利用函数的周期性，可将其他区间上的求值等问题，转化到已知区间上，进而解决问题．【例题选讲】[例1](1)若f (x )是R 上周期为2的函数，且满足f (1)＝1，f (2)＝2，则f (3)－f (4)＝__________．答案－1解析由f (x ＋2)＝f (x )可得f (3)－f (4)＝f (1)－f (2)＝1－2＝－1．(2)设f (x )是定义在R 上的周期为3的函数，当x ∈[－2，1)时，f (x )x 2－2，－2≤x ≤0，，0<x <1，则＝________．答案14解析由题意可得－2＝14，＝14．(3)设f (x )是定义在R 上且周期为2的函数，在区间[－1，1)上，f (x )＋a ，－1≤x <0，|25－x|，0≤x <1，其中a ∈R ．若5(2f -＝9(2f ，则f (5a )的值是________．答案－25解析：由题意可得5()2f -＝＝－12＋a，9()2f ＝|25－12|＝110，则－12＋a ＝110，a ＝35，故f (5a )＝f (3)＝f (－1)＝－1＋35＝－25．【高中数学函数专题】(4)函数f(x)满足f(x＋4)＝f(x)(x∈R)，且在区间(－2，2]上，f(x)cosπx2，0<x≤2，x＋12|，－2<x≤0，则f(f(15))的值为________．答案22解析由函数f(x)满足f(x＋4)＝f(x)(x∈R)，可知函数f(x)的周期是4，所以f(15)＝f(－1)＝|－1＋12|＝12，所以f(f(15))＝cosπ4＝22．(5)定义在R上的函数f(x)，满足f(x＋5)＝f(x)，当x∈(－3，0]时，f(x)＝－x－1，当x∈(0，2]时，f(x)＝log2x，则f(1)＋f(2)＋f(3)＋…＋f(2019)的值等于()A．403B．405C．806D．809答案B解析定义在R上的函数f(x)，满足f(x＋5)＝f(x)，即函数f(x)的周期为5.又当x∈(0，2]时，f(x)＝log2x，所以f(1)＝log21＝0，f(2)＝log22＝1.当x∈(－3,0]时，f(x)＝－x－1，所以f(3)＝f(－2)＝1，f(4)＝f(－1)＝0，f(5)＝f(0)＝－1．故f(1)＋f(2)＋f(3)＋…＋f(2019)＝403×[f(1)＋f(2)＋f(3)＋f(4)＋f(5)]＋f(2016)＋f(2017)＋f(2018)＋f(2019)＝403×1＋f(1)＋f(2)＋f(3)＋f(4)＝403＋0＋1＋1＋0＝405．【对点训练】1．已知f(x)是R上最小正周期为2的周期函数，且当0≤x<2时，f(x)＝x3－x，则函数y＝f(x)的图象在区间[0，6]上与x轴的交点个数为________．1．答案7解析因为当0≤x<2时，f(x)＝x3－x．又f(x)是R上最小正周期为2的周期函数，且f(0)＝0，则f(6)＝f(4)＝f(2)＝f(0)＝0．又f(1)＝0，∴f(3)＝f(5)＝f(1)＝0，故函数y＝f(x)的图象在区间[0，6]上与x轴的交点有7个．2．设f(x)是定义在R上且周期为2的函数，在区间[－1，1]上，f(x)1≤x<0，0≤x≤1，其中a，b∈R．若＝a＋3b的值为________．2．答案－10解析因为f(x)是定义在R上且周期为2的函数，所以f f(－1)＝f(1)，故＝，从而12b＋212＋1＝－12a＋1，即3a＋2b＝－2，①．由f(－1)＝f(1)，得－a＋1＝b＋22，即b＝－2a，②．由①②得a＝2，b＝－4，从而a＋3b＝－10．3．已知函数f(x)(1－x)，0≤x≤1，－1，1<x≤2，如果对任意的n∈N*，定义f n(x)＝{[()]}n ff f f x⋅⋅⋅个，那么f2019(2)的值为()A．0B．1C．2D．33．答案C解析∵f1(2)＝f(2)＝1，f2(2)＝f(1)＝0，f3(2)＝f(0)＝2，f4(2)＝f(2)＝1，∴f n(2)的值具有周期性，且周期为3，∴f2019(2)＝f3×673(2)＝f3(2)＝2，故选C．4．定义在R上的函数f(x)满足f(x＋6)＝f(x)．当－3≤x<－1时，f(x)＝－(x＋2)2；当－1≤x<3时，f(x)＝x.则f(1)＋f(2)＋f(3)＋…＋f(2022)＝__________．4．答案337解析由f(x＋6)＝f(x)可知，函数f(x)的周期为6，由已知条件可得f(1)＝1，f(2)＝2，f(3)＝f(－3)＝－1，f(4)＝f(－2)＝0，f(5)＝f(－1)＝－1，f(6)＝f(0)＝0，所以在一个周期内有f(1)＋f(2)＋f(3)＋…＋f(6)＝1＋2－1＋0－1＋0＝1，所以f(1)＋f(2)＋…＋f(2022)＝337×1＝337．5．已知函数f(x)的定义域为R．当x<0时，f(x)＝x3－1；当－1≤x≤1时，f(－x)＝－f(x)；当x>12时，f(6)＝()A．－2B．－1C．0D．25．答案D解析当x>12时，由可得当x>0时，f(x)＝f(x＋1)，所以f(6)＝f(1)，而f(1)＝－f(－1)，f(－1)＝(－1)3－1＝－2，所以f(6)＝f(1)＝2，故选D．6．对任意的实数x都有f(x＋2)－f(x)＝2f(1)，若y＝f(x－1)的图象关于x＝1对称，且f(0)＝2，则f(2019)＋f(2020)＝()A．0B．2C．3D．46．答案B解析∵y＝f(x－1)的图象关于x＝1对称，则函数y＝f(x)的图象关于x＝0对称，即函数f(x)是偶函数．令x＝－1，则f(－1＋2)－f(－1)＝2f(1)，即f(1)－f(1)＝2f(1)＝0，即f(1)＝0．则f(x＋2)－f(x)＝2f(1)＝0，即f(x＋2)＝f(x)，即函数的周期是2，又f(0)＝2，则f(2019)＋f(2020)＝f(1)＋f(0)＝0＋2＝2，故选B．考点二已知函数的周期性(隐性1)，求函数值【方法总结】已知函数的周期性(隐性1)，可利用周期性的性质结论1到结论6，先明确了周期再将其他区间上的求值转化到已知区间上，进而解决问题．【例题选讲】[例2](1)已知定义在R上的函数f(x)满足f(x＋1)＝－f(x)，且f(x)，－1＜x≤0，1，0＜x≤1，则下列函数值为1的是()A．f(2.5)B．f(f(2.5))C．f(f(1.5))D．f(2)答案D解析由f(x＋1)＝－f(x)知f(x＋2)＝－f(x＋1)＝f(x)，于是f(x)是以2为周期的周期函数，从而f(2.5)＝f(0.5)＝－1，f(f(2.5))＝f(－1)＝f(1)＝－1，f(f(1.5))＝f(f(－0.5))＝f(1)＝－1，f(2)＝f(0)＝1，故选D．(2)已知定义在R上的函数f(x)，对任意x∈R，都有f(x＋4)＝f(x)＋f(2)成立，若函数y＝f(x＋1)的图象关于直线x＝－1对称，则f(2018)的值为()A．2018B．－2018C．0D．4答案C解析依题意得，函数y＝f(x)的图象关于直线x＝0对称，因此函数y＝f(x)是偶函数，且f(－2＋4)＝f(－2)＋f(2)，即f(2)＝f(2)＋f(2)，所以f(2)＝0，所以f(x＋4)＝f(x)，即函数y＝f(x)是以4为周期的函数，f(2018)＝f(4×504＋2)＝f(2)＝0．(3)已知f(x)是定义在R上的函数，并且f(x＋2)＝1f(x)，当2≤x≤3时，f(x)＝x，则f(2022)＝__________．答案2解析由f(x＋2)＝1f(x)得f(x＋4)＝1f(x＋2)＝f(x)，所以T＝4，f(2022)＝f(4×505＋2)＝f(2)＝2．(4)已知定义在R上的函数f(x)满足f(2)＝2－3，且对任意的x都有f(x＋2)＝1－f(x)，则f(2020)＝________．答案－2－3解析由f(x＋2)＝1－f(x)，得f(x＋4)＝1－f(x＋2)＝f(x)，所以函数f(x)的周期为4，所以f (2020)＝f (4)．因为f (2＋2)＝1－f (2)，所以f (4)＝－1f (2)＝－12－3＝－2－ 3.故f (2020)＝－2－3．(5)已知定义在R 上的函数满足f (x ＋2)＝－1f (x )，当x ∈(0，2]时，f (x )＝2x －1．则f (1)＋f (2)＋f (3)＋…＋f (2018)的值为________．答案1348解析∵f (x ＋2)＝－1f (x )，∴f (x ＋4)＝－1f (x ＋2)＝f (x )，∴函数y ＝f (x )的周期T ＝4．又x ∈(0，2]时，f (x )＝2x －1，∴f (1)＝1，f (2)＝3，f (3)＝－1f (1)＝－1，f (4)＝－1f (2)＝－13．∴f (1)＋f (2)＋f (3)＋…＋f (2018)＝504[f (1)＋f (2)＋f (3)＋f (4)]＋f (504×4＋1)＋f (504×4＋2)＝＋3－11＋3＝1348．【对点训练】7．函数f (x )满足f (x ＋1)＝－f (x )，且当0≤x ≤1时，f (x )＝2x (1－x )，则5(2f 的值为()A ．12B ．14C ．－14D ．－127．答案A解析由f (x ＋1)＝－f (x )得f (x ＋2)＝f (x )，即函数f (x )的周期为2，则5()2f ＝2×12×＝12，故选A ．8．已知f (x )是定义在R 上的函数，且f (x ＋2)＝－f (x )．当x ∈(0，2)时，f (x )＝2x 2，则f (7)＝()A ．－2B ．2C ．－98D ．988．答案A解析由f (x ＋2)＝－f (x )，得f (7)＝－f (5)＝f (3)＝－f (1)＝－2．故选A ．9．已知定义在R 上的函数f (x )满足f (x )＝－f (x ＋2)，当x ∈(0，2]时，f (x )＝2x ＋log 2x ，则f (2019)＝()A ．5B ．12C ．2D ．－29．答案D解析由f (x )＝－f (x ＋2)，得f (x ＋4)＝f (x )，所以函数f (x )是周期为4的周期函数，所以f (2019)＝f (504×4＋3)＝f (3)＝f (1＋2)＝－f (1)＝－(2＋0)＝－2．10．已知函数f (x )对任意x ∈R ，都有f (x ＋6)＋f (x )＝0，y ＝f (x －1)的图象关于点(1，0)对称，且f (2)＝4，则f (2014)＝()A ．0B ．－4C ．－8D ．－1610．答案B解析由题意可知，函数f (x )对任意x ∈R ，都有f (x ＋6)＝－f (x )，∴f (x ＋12)＝f [(x ＋6)＋6]＝－f (x ＋6)＝f (x )，∴函数f (x )的周期T ＝12．把y ＝f (x －1)的图象向左平移1个单位得y ＝f (x －1＋1)＝f (x )的图象，关于点(0，0)对称，因此函数f (x )为奇函数，∴f (2014)＝f (167×12＋10)＝f (10)＝f (10－12)＝f (－2)＝－f (2)＝－4．故选B ．11．已知定义在R 上的函数f (x )满足f (4)＝2－3，且对任意的x 都有f (x ＋2)＝1－f (x )，则f (2018)＝()A ．－2－3B ．－2＋3C ．2－3D ．2＋311．答案A解析由f (x ＋2)＝1－f (x )得f (x ＋4)＝f (x )．所以函数f (x )的周期为4，所以f (2018)＝f (2)．又f (4)＝f (2＋2)＝1－f (2)＝2－3，所以－f (2)＝12－3＝2＋3，即f (2)＝－2－3，故选A ．12．已知f (x )是定义在R 上的函数，且满足f (x ＋2)＝－1f (x )，当2≤x ≤3时，f (x )＝x ，则________．12．答案52解析∵f (x ＋2)＝－1f (x )，∴f (x ＋4)＝f (x )，∴2≤x ≤3时，f (x )＝x ，∴＝52，∴＝52．考点三已知函数的周期性(隐性2)，求函数值【方法总结】已知函数的周期性(隐性2)，可利用周期性的性质结论7到结论9，先明确了周期再将其他区间上的求值转化到已知区间上，进而解决问题．【例题选讲】[例3](1)已知函数y ＝f (x )满足y ＝f (－x )和y ＝f (x ＋2)是偶函数，且f (1)＝π3，设F (x )＝f (x )＋f (－x )，则F (3)＝()A ．π3B ．2π3C ．πD ．4π3答案B解析由y ＝f (－x )和y ＝f (x ＋2)是偶函数知f (－x )＝f (x )，且f (x ＋2)＝f (－x ＋2)，则f (x ＋2)＝f (x －2)．∴f (x ＋4)＝f (x )，则y ＝f (x )的周期为4．所以F (3)＝f (3)＋f (－3)＝2f (3)＝2f (－1)＝2f (1)＝2π3．(2)函数f (x )的定义域为R ，且满足：f (x )是偶函数，f (x －1)是奇函数，若f (0.5)＝9，则f (8.5)等于()A ．－9B ．9C ．－3D ．0答案B解析因为f (x －1)是奇函数，所以f (－x －1)＝－f (x －1)，即f (－x )＝－f (x －2)．又因为f (x )是偶函数，所以f (x )＝－f (x －2)＝f (x －4)，故f (x )的周期为4，所以f (0.5)＝f (8.5)＝9．故选B ．(3)奇函数f (x )的定义域为R ，若f (x ＋1)为偶函数，且f (1)＝2，则f (4)＋f (5)的值为()A ．2B ．1C ．－1D ．－2解析：设g (x )＝f (x ＋1)，∵f (x ＋1)为偶函数，则g (－x )＝g (x )，即f (－x ＋1)＝f (x ＋1)．∵f (x )是奇函数，∴f (－x ＋1)＝f (x ＋1)＝－f (x －1)，∴f (x ＋2)＝－f (x )，f (x ＋4)＝f (x ＋2＋2)＝－f (x ＋2)＝f (x )，则f (4)＝f (0)＝0，f (5)＝f (1)＝2，∴f (4)＋f (5)＝0＋2＝2，故选A ．(4)已知f (x )是定义在R 上的奇函数，f (x ＋1)是偶函数，当x ∈(2，4)时，f (x )＝|x －3|，则f (1)＋f (2)＋f (3)＋f (4)＋…＋f (2020)＝________．答案解析因为f (x )为奇函数，f (x ＋1)为偶函数，所以f (x ＋1)＝f (－x ＋1)＝－f (x －1)，所以f (x＋2)＝－f (x )，所以f (x ＋4)＝－f (x ＋2)＝f (x )，所以函数f (x )的周期为4，所以f (4)＝f (0)＝0，f (3)＝f (－1)＝－f (1)．在f (x ＋1)＝f (－x ＋1)中，令x ＝1，可得f (2)＝f (0)＝0，所以f (1)＋f (2)＋f (3)＋f (4)＝0，所以f (1)＋f (2)＋f (3)＋f (4)＋…＋f (2020)＝0．(5)设函数f (x )是定义在R 上的奇函数，对任意实数x 有33()()22f x f x +=--成立．若f (1)＝2，则f (2)＋f (3)＝________．答案－2解析由33()()22f x f x +=--，且f (－x )＝－f (x )，知f (3＋x )＝f 32＋－f 32－＝－f (－x )＝f (x )，所以y ＝f (x )是周期函数，且T ＝3是其一个周期．因为f (x )为定义在R 上的奇函数，所以f (0)＝0，且f (－1)＝－f (1)＝－2，又T ＝3是y ＝f (x )的一个周期，所以f (2)＋f (3)＝f (－1)＋f (0)＝－2＋0＝－2．(6)已知f (x )是定义域为(－∞，＋∞)的奇函数，满足f (1－x )＝f (1＋x )．若f (1)＝2，则f (1)＋f (2)＋f (3)＋…＋f(50)等于()A．－50B．0C．2D．50答案C解析∵f(x)是奇函数，∴f(－x)＝－f(x)，∴f(1－x)＝－f(x－1)．∵f(1－x)＝f(1＋x)，∴－f(x －1)＝f(x＋1)，∴f(x＋2)＝－f(x)，∴f(x＋4)＝－f(x＋2)＝－[－f(x)]＝f(x)，∴函数f(x)是周期为4的周期函数．由f(x)为奇函数且定义域为R得f(0)＝0，又∵f(1－x)＝f(1＋x)，∴f(x)的图象关于直线x＝1对称，∴f(2)＝f(0)＝0，∴f(－2)＝0．又f(1)＝2，∴f(－1)＝－2，∴f(1)＋f(2)＋f(3)＋f(4)＝f(1)＋f(2)＋f(－1)＋f(0)＝2＋0－2＋0＝0，∴f(1)＋f(2)＋f(3)＋f(4)＋…＋f(49)＋f(50)＝0×12＋f(49)＋f(50)＝f(1)＋f(2)＝2＋0＝2，故选C．【对点训练】13．定义在R上的奇函数f(x)满足f(x＋1)是偶函数，且当x∈[0，1]时，f(x)＝x(3－2x)，则()A．12B．－12C．－1D．113．答案C解析∵y＝f(x)是定义在R上的奇函数，∴f(－x)＝－f(x)，∵函数y＝f(x＋1)是定义在R上的偶函数，∴f(－x＋1)＝f(x＋1)＝－f(x－1)，f(x＋2)＝－f(x)，可得f(x＋4)＝－f(x＋2)＝f(x)，则f(x)的周期是4，∴f－12＝－＝－12·(3－1)＝－1，故选C．14．已知偶函数f(x)的定义域为R，若f(x－1)为奇函数，且f(2)＝3，则f(5)＋f(6)的值为() A．－3B．－2C．2D．314．答案D解析因为f(x－1)是奇函数，所以f(－x－1)＝－f(x－1)，即f(－x)＝－f(x－2)．又因为f(x)是偶函数，所以f(x)＝－f(x－2)＝f(x－4)，故f(x)的周期为4，所以f(5)＋f(6)＝f(1)＋f(2)＝0＋3＝3．选D．15．偶函数y＝f(x)的图象关于直线x＝2对称，f(3)＝3，则f(－1)＝________．15．答案3解析解析：因为f(x)的图象关于直线x＝2对称，所以f(x)＝f(4－x)，f(－x)＝f(4＋x)．又f(－x)＝f(x)，所以f(x)＝f(4＋x)，则f(－1)＝f(4－1)＝f(3)＝3．16．已知奇函数f(x)的图象关于直线x＝3对称，当x∈[0，3]时，f(x)＝－x，则f(－16)＝________．16．答案2解析根据题意，函数f(x)的图象关于直线x＝3对称，则有f(x)＝f(6－x)，又由函数为奇函数，则f(－x)＝－f(x)，则有f(x)＝－f(6－x)＝f(x－12)，则f(x)的最小正周期是12，故f(－16)＝f(－4)＝－f(4)＝－f(2)＝－(－2)＝2．17．已知f(x)是定义在R上的奇函数，满足f(1＋x)＝f(1－x)，且f(1)＝a，则f(2)＋f(3)＋f(4)＝() A．0B．－a C．a D．3a17．答案B解析因为函数f(x)满足f(1＋x)＝f(1－x)，所以f(x)关于直线x＝1对称，所以f(2)＝f(0)，f(3)＝f(－1)，又f(x)是定义在R上的奇函数，所以f(0)＝0，又由f(1＋x)＝f(1－x)可得f(x＋1)＝f(1－x)＝－f(x－1)，所以f(x＋2)＝－f(x)，故f(x＋4)＝－f(x＋2)＝f(x)，因此，函数f(x)是以4为周期的周期函数，所以f(4)＝f(0)，又f(1)＝a，因此f(2)＋f(3)＋f(4)＝f(0)＋f(－1)＋f(0)＝－f(1)＝－a．故选B．18．函数y＝f(x)满足对任意x∈R都有f(x＋2)＝f(－x)成立，且函数y＝f(x－1)的图象关于点(1，0)对称，f(1)＝4，则f(2016)＋f(2017)＋f(2018)的值为________．18．答案4解析∵函数y＝f(x－1)的图象关于点(1，0)对称，∴f(x)是R上的奇函数，又f(x＋2)＝－f(x)，∴f(x＋4)＝－f(x＋2)＝f(x)，故f(x)的周期为4，∴f(2017)＝f(504×4＋1)＝f(1)＝4，∴f(2016)＋f(2018)＝f(2016)＋f(2016＋2)＝f(2016)－f(2016)＝0，∴f(2016)＋f(2017)＋f(2018)＝4．。

(3)由题意知 f(x)+g(x)=������1-1,① f(x)-g(x)=-������+1 1.② 由①②解得 f(x)=������21-1.
考点1
考点2
考点3
考点4
-16-
思考函数的奇偶性有哪几个方面的应用? 解题心得1.函数奇偶性的应用主要有:利用函数的奇偶性求函数 解析式;利用函数的奇偶性研究函数的单调性;利用函数的奇偶性 解不等式;利用函数的奇偶性求最值等. 2.已知函数的奇偶性求函数的解析式,往往要抓住奇偶性讨论函 数在各个分区间上的解析式,或充分利用奇偶性产生关于f(x)的方 程,从而可得f(x)的解析式.
随堂巩固
-7-
知识梳理 考点自诊
2.(2018陕西宝鸡中学三模,2)函数 f(x)=4���2���+������ 1 的图像( C )
A.关于原点对称
B.关于x轴对称
C.关于y轴对称
D.关于直线y=x对称
解析:∵f(x)=4���2���+������ 1=2x+21������,且
f(-x)=2-x+21-������
2.3 函数的奇偶性与周期性
知识梳理 考点自诊
随堂巩固
-2-
1.函数的奇偶性
奇偶性 定 义
图像特点
如果对于函数 f(x)的定义域内任意一 偶函数 个 x,都有 f(-x)=f(x) ,那么函数 关于 y轴 对称
f(x)是偶函数
如果对于函数 f(x)的定义域内任意一 奇函数 个 x,都有 f(-x)=-f(x) ,那么函数 关于 原点 对称
(3)若f(x+a)=f(x-a),则T=2a;一般地,若f(x+a)=f(x-b),则T=|a+b|;

A.－1 B.0 C.1 D.2
解析：∵f(x)为定义在R上的奇函数， ∴f(0)＝0 又 f(x＋4)＝f(x)，∴f(8)＝f(4)＝f(0)＝0
题型三、函数性质的综合应用
命题点1：求函数值或函数解析式 例3：函数f(x)是定义在R上的奇函数，当x∈(－∞，0)
时，f(x)＝2x3＋x2，则f(2)＝__1_2___
2
由图像可知，
－2 O
x
满足不等式x f(x)<0的解为：
x<－2或x>2
答案：(－∞，－2)∪(2，＋∞)
三、归纳总结
1.函数的奇偶性是函数在其定义域上的整体性质，定义 域关于原点对称是函数具有奇偶性的必要不充分条 件．因此，判断函数的奇偶性，一要看定义域是否关于 原点对称；二要看f(x)与f(－x)的关系． 2.奇函数在关于原点对称的区间上具有相同的单调性； 偶函数在关于原点对称的区间上具有相反的单调性.
一、基础知识梳理
3.奇(偶)函数的性质
(2)奇函数在关于原点对称的区间上具有相同的单调性； 偶函数在关于原点对称的区间上具有相反的单调性. (3)若函数f(x)是奇函数，且在x=0处有定义，则f(0)=0； (4)在公共定义域内有： ①奇函数±奇函数＝奇函数；
②偶函数±偶函数＝偶函数； ③奇函数×奇函数＝偶函数；
命题点1：求函数值或函数解析式 对点训练3：若函数f(x)是定义在R上的周期为2的奇 函数，当0<x<1时，f(x)＝4x，则
f（－2.5）＋f(2)＝__－__2__
解析：∵f(x)是定义在R上的周期为2的奇函数，
∴f(2)＝f(0)＝0， ∵ 当 0<x<1时，f(x)＝4x ， ∴f(－2.5)＝f(－0.5) ＝－f(0.5) ＝－40.5 ＝－（22）0.5

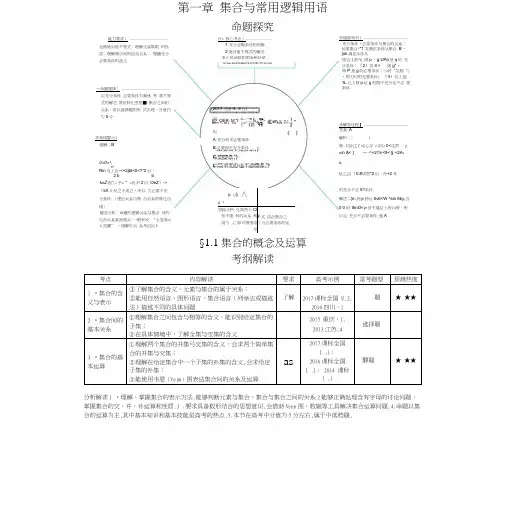
第一章 集合与常用逻辑用语命题探究§1.1集合的概念及运算考纲解读考点内容解读要求高考示例常考题型预测热度 1 •集合的含义与表示①了解集合的含义、元素与集合的属于关系；②能用自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题了解 2017课标全国 U,2;2016四川，1题★ ★★2 •集合间的基本关系① 理解集合之间包含与相等的含义，能识别给定集合的子集；② 在具体情境中，了解全集与空集的含义2015 重庆，1; 2013江苏,4 选择题3 •集合的基本运算① 理解两个集合的并集弓交集的含义，会求两个简单集合的并集与交集；② 理解在给定集合中一个子集的补集的含义,会求给定子集的补集；③ 能使用韦恩（Verm ）图表达集合间的关系及运算as2017课标全国I ,1； 2016课标全国 I ,1； 2014 课标I ,1醪题 ★ ★★分析解读1 •理解、掌握集合的表示方法.能够判断元素与集合、集合与集合之间的关系2能够正确处理含有字母的讨论问题， 掌握集合的交、并、补运算和性质.3 .要求具备数形结合的思想意识,会借助Venn 图、数轴等工具解决集合运算问题.4.命题以集 合的运算为主,其中基本知识和基本技能是高考的热点.5.本节在高考中分值为5分左右,属于中低档题.能力要求） ------------------- 会僧绝对值不等式；理解正裟映数 的性质；理解築合间的包含关系； 理舗充分必要条件的盘义卢> 核心考点） -------------1.充分必製条件的判断 2绝对值不等式的解法 3止弦函数的图彖和性质〜命题规律〕 ------------------------ 以充分条件.必耍条件为栽休.考 賁不等式的解法.零价转化思想■ 集合之间的关系，常以选择題的形 式岀现，分值约为5分孕易错警示} 错解：B0<0<^.nRin 氐丄台-<+2jbt<0<?*2后，2 b b keZ.因为-乎+"”<氐尹2后 OeZ ）->（kX 讣反之不成立•所以 为必耍不充分条件.（逻出关系与集 合关系的转化岀错〉错因分析：命題的逻辑关系与集合 何的包含关系紧密相关.一般来说 “小范国=> 大范圃” •错解中关 系考出反r申储备知识） ----------------------充分条件•必耍条件与集合的关系： 如果集合**1龙满圧条件从集合 B ・{xk 満足朵件从则仏⑴若*6,則p ・g,UPp 是q 的 充分条件；（2）若4 = 則g*・ 即P 是g 的必要条件；⑶若“乩则 勺•即刃切的充要条件；（4）若人创 1L 必人则p 址g 的既不充分也不必 要条件(2017天津.4. 5分)的A. 充分何不必要条件B. 必要而不充分条件C.充要条件m ch 八 u 、思路分析 化简两个Cl知不第 何的关系.利用为 义,即可得別结论F 式.结合集合之 ［分必耍条件的定孕解答过程】 ----------------------答案:A 解析：||林-卡計辽C 说心寻 <寻台0<氐罟， p«in &< } — -^+2/TK <9< § +2A ：x,址乙由（0.#烘罟*2后，舟+2耳的充分不必5?条件.解法二|e -誇|v 誇台0v6<W ^sin 6ky,当0 0时.8inO<y f 但不漏足卜誇|<誇，所以足 充分不必耍条件.选AL ）•既不充分也不必耍条件没OER. M "I 亠二lv IT ■・ 址sin 火亠"12五年高考考点一集合的含义与表示1.（2017 课标全国U 25 分）设集合A二{124}后{xlx—x+nrf}.若ACB={1},则B=（）A.{1,-3}答案c2.（2016四川，1,5分）设集合gxl-20W2},Z为整数集，则集合AQZ中元素的个数是（）A.3B.4C.5D.6答案C3.（2013山东,2,5分）已知集合A二{0,1,2},则集合B={x-y lx^A,yWA}中元素的个数是（）A.lB.3C.5D.9答案C4.(2017江苏,1,5分)已知集合A二{l,2},B={a,a*3}.若ACB={1},则实数a的值为 __________答案1考点二集合间的基本关系1.(2015重庆,1,5分)已知集合A二{123}后{2,3},则( )A.A=BB.Ai^B=nC.AOBD.BOA答案D2.(2013江苏,4,5分)集合{・1,0,1}共有_______ 个子集.答案8考点三集合的基本运算1.(2017课标全国I ,1,5分)已知集合A={xlx<l},B={xl3x<l} )A.AHB=(xlx<0}B.AUB=RC.AUB=(xlx>l}D.AnB=D答案A2.(2017 课标全Bin,1,5 分)已知集合A={(x,y)lx2+y=l}»B={(x,y)ly=x},则ACB 中元素的个数为(A.3B.2C.lD.O答案B3.(2017 天津,1,5 分)设集合A={l,2,6)»B={2,4),C={xeR|-l<x<5} JU(AUB)nc=( )A.{2}B.{1,2,4}C.{1,2,4,6}D.{xERI・lWxW5}答案B4.(2016 课标全国I ,1,5 分)设集合A={x I x2-4x+3<0},B={x 12x-3>0},则ACB=( )A. B. C. D.答案D5.(2016课标全国U ,2,5 分)已知集合A={l,2,3),B={xl(x+l)(x-2)<0,xez},MAUB=( )A.{1}B.{1,2}C.{0,1,2,3}D.{-1,0,1,2,3}答案C6.(2016 天津,1,5 分)已知集合A={l,2,3,4),B={yly=3x-2,xeA},J!!lAnB=( )A.{1}B.{4}C.{1,3}D.{1,4}答案D7.(2014课标I ,1,5 分)已知集合A={xlx2-2x-3^0},B={xl-2^x<2),则ACB=( )A.[-2,-1]B.[-l,2)C.[-l,l]D.[l,2)答案A教师用书专用(8—24)8.(2017北京,1,5分)若集合A={xl-2<x<l},B={xlx<-1 或x>3},则AAB=( )A.(xl-2<x<-l}B.(xl-2<x<3)C.{xl-1<X<1}D.{xll<x<3}答案A9.(2017浙江,1,5 分)已知集合P={xl-l<x<l} ,Q={xl0<x<2}，则PUQ=( )A.(-1,2)B.(0,l)C.(-l,0)D.(l,2)答案A10.(2017山东,1,5分)设函数y二的定义域为A,函数y=ln(l -x)的定义域为B,则AAB=()A.(1,2)B.(l,2]C.(-2,l)D.[-2,l)答案D11.(2016课标全国皿,1,5分)设集^S={xl(x-2)(x-3)>0},T={xlx>0},则S(1T=()A.[2,3]B.(-°O,2]U[3,+OO)C.[3,+S)D.(0,2]U[3,+B)答案D12.(2016 北京，1,5 分)已知集合A={xllxl<2},B={-l,0,l,2,3},则AQB=( )A.(0,1)B.(0,l,2}C.{-1,0,1}D.{-1,0,1,2}答案C13.(2016 浙江,1,5 分)已知集合P二{xURIlWxW3},Q={xWRIx2p4}、则PU((R Q)=( )A.[2,3]B.(・2,3]C.[l,2)D.(・8,-2]U[1,+OO)答案B14.(2016 山东,2,5分)设集合A二{yly二2x,xER},B={xlx2-l<0},则AUB=( )A.(-1,1)B.(0,l)C.(-l,+°°)D.(0,+8)答案C15.(2015 课标n, 1,5 分)已知集合A={-2,-l,0,l,2),B={xl(x-l)(x+2)<0},则AQB=( )A.{-1,0} C.{-1,0,1} D.(0,l,2}答案A16.(2015 天津,1,5 分)已知全集U二{1,2,3,4,5,6,7,8},集合A二{2,3,5,6},集合,3,4,6,7},则集合 A 门血()A.{2,5}B.(3,6}C.(2,5,6}D.{2,3,5,6,8}答案A17.(2015福建，1,5分)若集合AMi,i2,i',r}(i是虚数单位)，隹{1,・1},则人门3等于()A.{-1}B.{1}C.(l,-1}D.口答案C18.(2015 四川，1,5 分)设集合A二{xl(x+l)(x-2)<0},集合B={xll<x<3),则AUB=( )A.(xI -l<x<3}B.(xI -1<X<1}C.(xIl<x<2}D.(xl2<x<3)答案A19.(2015 广东,1,5 分)若集合M={xl(x+4)(x+l)=0},N={xl(x-4)(x-l)=0},则MCN=( )A.{1,4}B.{-l,-4}C.{0}D.口答案D20.(2014课标II ,1,5 分)设集合归{0,l,2},N={xlx2.3x+2W0},5!!lMCN=( )A.{1}B.{2}C.(0,l}D.{1,2)答案D21.(2014 辽宁,1,5 分)已知全集U二R,A二{xlxW0},B={xlxMl},则集合]u(AUB)=( )A. {x 1x^0} BjxlxWl}C.{xlOWxWl}D.(xl0<x<l}答案D22.(2014 浙江，1,5 分)设全集U二{xWNIxM2},集合A二{x^NIx 空5},则[山二( )A.口B.{2}C.{5}D.{2,5}答案B23.(2015江苏,1,5分)已知集合A二{1,2,3}后{2,4,5},则集合人餌中元素的个数为_________ .答案524.(2016 江苏,1,5 分)已知集合A={-l,2,3,6},B={xl-2<x<3},则AAB= ___________ .答案{-1,2}三年模拟A组2016—2018年模拟•基础题组考点一集合的含义与表示1.(2018 广东茂名化州二模」)设集合A二{・101},B={xlx>0,xWA}^!lB=( )A.（-LO） C.（OJ） D.{1}答案D2・（2017河北冀州第二次阶段考试J）若集合A=（xlx2-7x<0, x丘N）则集合匸中元素的个数为（）A.lB.2C.3D.4答案D考点二集合间的基本关系3.（2018四川成都龙泉一中月考,2）已知集合A=,B= {xIax+1 =0},且BUA,则a的取值组成的集合为（）AJ-3,2} BJ-3,O,2} C.{3,・2} D・{3,0,・2}答案D4.(2017河南南阳、信阳等六市一模,1)已知集合A={ (x, y) I y • =0},B={ (x, y) I x2+y2= 1}，C=A C B,则C的子集的个数是( )A.OB.lC.2D.4答案c考点三集合的基本运算5.（2018豫南豫北第二次联考，1）已知集合A二{yIy二2*},B二{xIy=},则A门B=（A・{yly>l}答案BB.{yly>l}C.{yly>0} D・{ylyP0}6.（2018江西重点中学第一次联考，1 ）已知集合归，则帥二（）A.（XI - 1<X<1}B. {x I - l<x^l}C. {xlx<-l 或xMl}D.{xlxW・l 或xMl}答案C7.（2017广东惠州第三次调研,1）已知全集hR,集合A二{1,2,3,4,5},B= {x丘RIx鼻2},则图中阴影部分所表示的集合为（A.（0,l,2）B.（0,l）C.{1,2）D.{1）答案D8.（2017河南濮阳第二次检测,13）已知集合A=（-l,a},B={3a,b},gAUB={-l,0,l},则& _____________答案0B组2016—2018年模拟•提升题组（满分:35分时间:20分钟）一、选择题（每小题5分，共30分）1.（2018 广东茂名化州二模,1）若集合A二{0,1}后{yly 二2x,x^A},则（bA）QB=（）AJO} B•⑵ C.{2,4} D.{0丄2}答案B2.（2018吉林榆树第一高级中学第三次模拟J）设全集U二{1,3,5,6,9},A二{3,6,9}、则图中阴影部分表示的集合是（）A・{1,3,5}答案D3.（2018 四川南充一诊,2）已知集合A二{（x,y）ly=f（x）},B={（x,y）lx=l},则ACB 中的元素有（）A.1个B.1个或2个C.至多1个D.可能2个以上答案C4.（2017湖南永州二模,2）已知集合P二{xl JWxWl},归心},若PQM二□，则a的取值范围是（）C.[-l,l]D.（4,-1）U（1,+8）答案D5.（2017河北唐山摸底,1）已知集合AC （1,2,3,4,5},且AC{1,2,3}={1,2},则满足条件的集合A的个数为（）A.2B.4C.8D.16答案B6.（2016江西南昌十所省重点中学二模,2）设集合A=,B={xly=ln（x2-3x）},5!!jAnB中元素的个数是（）A.lB.2C.3D.4答案A 二、填空题（共5分）7.（2017江西九江地区七校联考,14）设A, B是非空集合淀义A®B={ x I x丘A U B且x电⑴B},已知壯{y I y=・x'+2x,0<x<2}, N二{y I y二2’ 则M®N二.答案U（l,+<XjC组2016—2018年模拟•方法题组方法1与集合元素有关问题的解题方略1.（2016湖南衡阳八中一模,1）已知集合A二{0,1} ,B={zlz二x+y,xWA,yWA}，则集合B的子集个数为（）A・3 B.4 C.7 D.8答案D方法2集合间的基本关系的解题方法2.（2017河北衡水中学七调,1）已知集合A二{x11 og2X<l},B={xl0<x<c}，若AUB=B,则c的取值范围是（）A.（0,1]B.[l,+oo）C.（0,2]D.[2,+oo）答案D3.（2018河北衡水中学模拟，13）已知含有三个实数的集合既可表示成,又可表示成{a2,a+b,0}，则a20,W0,7等于________答案方法3集合的基本运算的解题方法4.(2017安徽淮北第二次模拟,2)已知全集U=R，集合M={ x I x+2诈0} ,N={xll ogi( x・1 )<1}、若集合M C ((uN)二{x I x二1或x M 3},那么a的取值为()A. a=B.aWC. a=-D.aM答案C5.（人教 A 必1,—,1・1A,7,变式）设全集U={xWNIxW8},集合4{1,3,7},B={2,3,8},则（CuA）门（应）=（）A.{1,2,7,8}B.{4,5,6}C.{0,4,5,6}D.{0,3,456}答案C方法4求解集合新定义问题的技巧6.（2018陕西西安长安质检,2）若x & A,且& A侧称A是伙伴关系集合,集合归的所有非空子集中具有伙伴关系的集合的个数是A.31B.7C.3D.1答案B7.(2017湖北武昌一模,1)设A,B是两个非空集合淀义集合A・B={xlxUA,且x年B}.若A二{x£NI0WxW5> ,B={xl/・7x+l(kO},则4 B=()A.(0,1)B.{1,2)C.(0,l,2)D.(0,1,2,5}答案D。

那么函数f(x)就叫做偶函数
一般地，设函数f(x)的定义域为D，如果 奇函数 ∀x∈D，都有－x∈D，且_f_(_－__x_)＝__－__f_(x_)_， 关于_原__点__对称
那么函数f(x)就叫做奇函数
知识梳理
2.周期性 (1)周期函数：一般地，设函数f(x)的定义域为D，如果存在一个非零常数 T，使得对每一个x∈D都有x＋T∈D，且__f(_x_＋__T_)＝__f_(_x_) _，那么函数y＝f(x) 就叫做周期函数，非零常数T叫做这个函数的周期. (2)最小正周期：如果在周期函数f(x)的所有周期中存在一个_最__小__的正数， 那么这个_最__小__正__数__就叫做f(x)的最小正周期.
√A.f(2 023)＝0 √B.f(x)的值域为[－1,2]
C.f(x)在[4,6]上单调递减
D.f(x)在[－6,6]上有8个零点
f(2 023)＝f(506×4－1)＝f(－1)＝f(1)＝0，所以A正确； 当x∈[0,2]时，f(x)＝2x－2单调递增， 所以当x∈[0,2]时，函数的值域为[－1,2]， 由于函数是偶函数，所以函数的值域为[－1,2]，所以B正确； 当x∈[0,2]时，f(x)＝2x－2单调递增， 又函数的周期是4， 所以f(x)在[4,6]上单调递增，所以C错误；
教材改编题
2.已知函数y＝f(x)是奇函数，且当x>0时，有f(x)＝x＋2x，则f(－2)＝_－__6_.
因为函数y＝f(x)是奇函数，且当x>0时，有f(x)＝x＋2x， 所以f(－2)＝－f(2)＝－(2＋4)＝－6.
教材改编题
3.已知函数f(x)是定义在R上的周期为4的奇函数，若f(1)＝1，则f(2 023)＝ _－__1__.

A.f(x)＝x＋sin x
√B.f(x)＝(x－1)
x＋1 x－1
C.f(x)＝ln( x2＋1－x)
D.f(x)＝2x＋21x
A项，f(x)的定义域为R，由f(－x)＝－x＋sin(－x)＝－f(x)知，f(x)为 奇函数； B 项，令xx＋ －11≥0，解得 x≤－1 或 x>1，即函数 f(x)的定义域为(－∞， －1]∪(1，＋∞)，不关于原点对称，即 f(x)为非奇非偶函数； C 项，因为 x2＋1>x2，所以 x2＋1－x>0 恒成立，即 f(x)的定义域为
微拓展
抽象函数 抽象函数主要研究赋值求值、证明函数的性质、解不等式等，一般通过 代入特殊值求值、通过f(x1)－f(x2)的变换判定单调性、出现f(x)及f(－x)判 定抽象函数的奇偶性、换x为x＋T确定周期性. (1)判断抽象函数单调性的方法 ①若给出的是“和型”抽象函数f(x＋y)＝…，判断符号时要变形为f(x2)－ f(x1)＝f((x2－x1)＋x1)－f(x1)或f(x2)－f(x1)＝f(x2)－f((x1－x2)＋x2)；
典例 (1)(多选)已知函数f(x)的定义域为R，且f(x＋y)＝f(x)＋f(y)，当x>0
时，f(x)>0，且满足f(2)＝1，则下列说法正确的是
√A.f(x)为奇函数 √B.f(－2)＝－1
C.不等式f(2x)－f(x－3)>－2的解集为(－5，＋∞)
D.f(－2 024)＋f(－2 023)＋…＋f(0)＋…＋f(2 023)＋f(2 024)＝2 023
所以f(x1)－f(x2)＝f(x1)＋f(－x2)＝f(x1－x2)， 又因为x1>x2，所以x1－x2>0， 所以f(x1－x2)>0，即f(x1)>f(x2)， 所以f(x)在R上单调递增，因为f(－2)＝－1， 所以f(－4)＝f(－2－2)＝2f(－2)＝－2， 由f(2x)－f(x－3)>－2， 可得f(2x)>f(x－3)＋f(－4)，