二级数学下册同步练习题(2017)

2017年上海市杨浦区高考数学二模试卷一、填空题1．（4分）三阶行列式中，5的余子式的值是．2．（4分）若实数ω＞0，若函数f（x)=cos(ωx）+sin（ωx）的最小正周期为π，则ω=．3．（4分）已知圆锥的底面半径和高均为1，则该圆锥的侧面积为．4．（4分）设向量=（2，3）,向量=（6,t），若与夹角为钝角,则实数t的取值范围为．5．（4分)集合A={1，3,a2｝,集合B=｛a+1，a+2}，若B∪A=A,则实数a=．6．（4分）设z1、z2是方程z2+2z+3=0的两根，则｜z1﹣z2|=．7．设f（x）是定义在R上的奇函数,当x＞0时，f（x）=2x﹣3，则不等式f（x)＜﹣5的解为．8．若变量x、y满足约束条件,则z=y﹣x的最小值为．9．小明和小红各自掷一颗均匀的正方体骰子，两人相互独立地进行，则小明掷出的点数不大于2或小红掷出的点数不小于3的概率为．10．设A是椭圆+=1（a＞0）上的动点，点F的坐标为（﹣2,0）,若满足|AF｜=10的点A有且仅有两个，则实数a的取值范围为．11．已知a＞0，b＞0,当（a+4b）2+取到最小值时，b=．12．设函数f a（x）=|x｜+｜x﹣a|，当a在实数范围内变化时，在圆盘x2+y2≤1内，且不在任一f a(x）的图象上的点的全体组成的图形的面积为．二、选择题13．设z∈C且z≠0，“z是纯虚数”是“z2∈R”的(）A．充分非必要条件 B．必要非充分条件C．充要条件D．既不充分也不必要条件14．设等差数列｛a n}的公差为d，d≠0，若｛a n}的前10项之和大于其前21项之和，则（）A．d＜0 B．d＞0 C．a16＜0 D．a16＞015．如图，N、S是球O直径的两个端点，圆C1是经过N和S点的大圆，圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆，圆C1和C2交于点A、B，圆C1和C3交于点C、D，设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长，则a、b、c的大小关系为（）A．b＞a=c B．b=c＞a C．b＞a＞c D．b＞c＞a16．对于定义在R上的函数f(x），若存在正常数a、b，使得f（x+a）≤f(x)+b 对一切x∈R均成立,则称f（x）是“控制增长函数”,在以下四个函数中：①f （x)=x2+x+1；②f（x）=; ③f（x）=sin（x2）；④f（x）=x•sinx．是“控制增长函数"的有（）A．②③B．③④C．②③④D．①②④三、解答题17．（14分）如图，正方体ABCD﹣A1B1C1D1中,AB=4，P、Q分别是棱BC与B1C1的中点．(1）求异面直线D1P和A1Q所成角的大小；(2）求以A1、D1、P、Q四点为四个顶点的四面体的体积．18．（14分）已知函数f（x）=．（1)判断函数f(x）的奇偶性,并证明；(2）若不等式f（x）＞log9（2c﹣1）有解，求c的取值范围．19．（14分)如图，扇形ABC是一块半径为2千米，圆心角为60°的风景区，P 点在弧BC上,现欲在风景区中规划三条商业街道，要求街道PQ与AB垂直,街道PR与AC垂直，线段RQ表示第三条街道．(1）如果P位于弧BC的中点，求三条街道的总长度；（2）由于环境的原因,三条街道PQ、PR、RQ每年能产生的经济效益分别为每千米300万元、200万元及400万元,问：这三条街道每年能产生的经济总效益最高为多少？（精确到1万元）20．（16分）设数列｛a n｝满足a n=A•4n+B•n，其中A、B是两个确定的实数，B ≠0．（1)若A=B=1，求{a n｝的前n项之和;（2）证明：{a n}不是等比数列;（3）若a1=a2，数列｛a n}中除去开始的两项之外,是否还有相等的两项？证明你的结论．21．（18分)设双曲线Γ的方程为x2﹣=1,过其右焦点F且斜率不为零的直线l1与双曲线交于A、B两点,直线l2的方程为x=t，A、B在直线l2上的射影分别为C、D．（1）当l1垂直于x轴，t=﹣2时，求四边形ABDC的面积;（2）当t=0，l1的斜率为正实数，A在第一象限，B在第四象限时，试比较和1的大小,并说明理由；(3）是否存在实数t∈（﹣1，1），使得对满足题意的任意直线l1，直线AD和直线BC的交点总在x轴上，若存在，求出所有的t的值和此时直线AD与BC交点的位置；若不存在，说明理由．2017年上海市杨浦区高考数学二模试卷参考答案与试题解析一、填空题1．三阶行列式中，5的余子式的值是﹣12．【考点】OU：特征向量的意义．【分析】去掉5所在行与列，即得5的余子式，从而求值．【解答】解:由题意，去掉5所在行与列得:=﹣12故答案为﹣12．【点评】本题以三阶行列式为载体，考查余子式，关键是理解余子式的定义．2．若实数ω＞0，若函数f(x)=cos(ωx）+sin（ωx）的最小正周期为π，则ω=2．【考点】H1：三角函数的周期性及其求法．【分析】利用两角和的正弦公式化简函数的解析式,再利用正弦函数的周期性，求得ω的值．【解答】解:实数ω＞0，若函数f（x）=cos（ωx)+sin(ωx)=sin（ωx+）的最小正周期为π,∴=π,∴ω=2，故答案为：2．【点评】本题主要考查两角和的正弦公式，正弦函数的周期性，属于基础题．3．已知圆锥的底面半径和高均为1，则该圆锥的侧面积为．【考点】L5：旋转体（圆柱、圆锥、圆台)．【分析】首先根据底面半径和高利用勾股定理求得母线长，然后直接利用圆锥的侧面积公式代入求出即可．【解答】解：∵圆锥的底面半径为1，高为1，∴母线长l为:=，∴圆锥的侧面积为:πrl=π×1×=π,故答案为：π．【点评】题考查了圆锥的侧面积的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键．4．设向量=（2，3）,向量=(6，t），若与夹角为钝角，则实数t的取值范围为（﹣∞，﹣4）．【考点】9S：数量积表示两个向量的夹角．【分析】由题意可得＜0，且、不共线,即，由此求得实数t的取值范围．【解答】解：若与夹角为钝角，向量=（2，3），向量=（6，t）,则＜0,且、不共线，∴，求得t＜﹣4，故答案为：（﹣∞，﹣4）．【点评】本题主要考查两个向量的数量公式，两个向量共线的性质，属于基础题．5．集合A={1，3，a2},集合B=｛a+1，a+2｝，若B∪A=A，则实数a=2．【考点】18:集合的包含关系判断及应用．【分析】根据并集的意义，由A∪B=A得到集合B中的元素都属于集合A，列出关于a的方程,求出方程的解得到a的值．【解答】解：由A∪B=A,得到B⊆A，∵A=｛1,3，a2},集合B={a+1,a+2},∴a+1=1，a+2=a2，或a+1=a2，a+2=1，或a+1=3,a+2=a2，或a+1=a2，a+2=3，解得：a=2．故答案为2．【点评】此题考查了并集的意义,以及集合中元素的特点．集合中元素有三个特点，即确定性，互异性，无序性．学生做题时注意利用元素的特点判断得到满足题意的a的值．6．设z1、z2是方程z2+2z+3=0的两根，则|z1﹣z2｜=2．【考点】A7：复数代数形式的混合运算．【分析】求出z,即可求出|z1﹣z2|．【解答】解:由题意，z=﹣1±i，∴|z1﹣z2|=｜2i|=2，故答案为2．【点评】本题考查复数的运算与球模,考查学生的计算能力，比较基础．7．设f（x）是定义在R上的奇函数，当x＞0时,f（x）=2x﹣3，则不等式f（x)＜﹣5的解为（﹣∞，﹣3)．【考点】3L：函数奇偶性的性质．【分析】根据函数奇偶性的性质求出当x＜0的解析式，讨论x＞0，x＜0，x=0,解不等式即可．【解答】解:若x＜0，则﹣x＞0，∵当x＞0时，f(x）=2x﹣3，∴当﹣x＞0时，f（﹣x)=2﹣x﹣3，∵f（x）是定义在R上的奇函数，∴f（﹣x)=2﹣x﹣3=﹣f(x),则f（x）=﹣2﹣x+3，x＜0,当x＞0时，不等式f(x）＜﹣5等价为2x﹣3＜﹣5即2x＜﹣2，无解，不成立；当x＜0时，不等式f（x)＜﹣5等价为﹣2﹣x+3＜﹣5即2﹣x＞8,得﹣x＞3，即x＜﹣3；当x=0时,f（0）=0，不等式f(x）＜﹣5不成立，综上,不等式的解为x＜﹣3．故不等式的解集为(﹣∞，﹣3）．故答案为（﹣∞，﹣3）．【点评】本题主要考查不等式的解集的求解,根据函数奇偶性的性质求出函数的解析式是解决本题的关键．8．若变量x、y满足约束条件，则z=y﹣x的最小值为﹣4．【考点】7C：简单线性规划．【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标,代入目标函数得答案．【解答】解:由约束条件作出可行域如图,联立,解得A（8，4),化目标函数z=y﹣x,得y=x+z，由图可知，当直线y=x+z过点A（8，4）时，直线在y轴上的截距最小，z有最小值为﹣4．故答案为：﹣4．【点评】本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．9．小明和小红各自掷一颗均匀的正方体骰子，两人相互独立地进行，则小明掷出的点数不大于2或小红掷出的点数不小于3的概率为．【考点】CC：列举法计算基本事件数及事件发生的概率．【分析】先求出基本事件总数n=6×6=36，再求出小明掷出的点数不大于2或小红掷出的点数不小于3包含的基本事件个数m=2×6+6×4﹣2×4=28，由此能求出小明掷出的点数不大于2或小红掷出的点数不小于3的概率．【解答】解：小明和小红各自掷一颗均匀的正方体骰子,两人相互独立地进行,基本事件总数n=6×6=36，小明掷出的点数不大于2或小红掷出的点数不小于3包含的基本事件个数:m=2×6+6×4﹣2×4=28，∴小明掷出的点数不大于2或小红掷出的点数不小于3的概率为：p==．故答案为：．【点评】本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．10．设A是椭圆+=1（a＞0）上的动点，点F的坐标为(﹣2，0），若满足｜AF|=10的点A有且仅有两个，则实数a的取值范围为8＜a＜12．【考点】K4：椭圆的简单性质．【分析】由题意，F是椭圆的焦点，满足|AF|=10的点A有且仅有两个，可得a ﹣2＜10＜a+2,即可得出结论．【解答】解：由题意，F是椭圆的焦点，∵满足｜AF|=10的点A有且仅有两个，∴a﹣2＜10＜a+2，∴8＜a＜12，故答案为：8＜a＜12．【点评】本题考查椭圆的方程与性质，考查学生的计算能力，比较基础．11．已知a＞0，b＞0，当(a+4b）2+取到最小值时，b=．【考点】7F:基本不等式．【分析】根据基本不等式，，a=4b时取等号，进而得出，进一步可求出a=1,时，取到最小值，即求出了此时的b的值．【解答】解:∵a＞0，b＞0；∴，当a=4b时取“=”；∴（a+4b)2≥16ab；∴=8，当，即，a=1时取“=”；此时，b=．故答案为：．【点评】考查基本不等式，注意基本不等式等号成立的条件，不等式的性质．12．设函数f a(x)=｜x|+|x﹣a|,当a在实数范围内变化时，在圆盘x2+y2≤1内，且不在任一f a（x）的图象上的点的全体组成的图形的面积为．【考点】7F：基本不等式．【分析】根据题意，分析可得函数f a（x）=｜x｜+|x﹣a|（当a在实数范围内变化）的图象，进而可得在圆盘x2+y2≤1内，且不在任一f a（x）的图象上的点单位圆的，由圆的面积公式计算可得答案．【解答】解：根据题意，对于函数f a（x）=|x｜+｜x﹣a|，当a变化时，其图象为在圆盘x2+y2≤1内，且不在任一f a（x）的图象上的点单位圆的,则其面积S=×π=；故答案为：．【点评】本题考查函数的图象，关键是分析函数f a(x）=｜x｜+|x﹣a|（当a在实数范围内变化)的图象．二、选择题13．设z∈C且z≠0,“z是纯虚数"是“z2∈R”的（）A．充分非必要条件 B．必要非充分条件C．充要条件D．既不充分也不必要条件【考点】2L：必要条件、充分条件与充要条件的判断．【分析】z∈C且z≠0，“z是纯虚数”⇒“z2∈R"，反之不成立,例如取z=2．即可判断出结论．【解答】解：∵z∈C且z≠0，“z是纯虚数”⇒“z2∈R”，反之不成立，例如取z=2．∴“z是纯虚数”是“z2∈R”的充分不必要条件．故选：A．【点评】本题考查了纯虚数的定义、复数的运算法则、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．14．设等差数列｛a n}的公差为d,d≠0，若{a n}的前10项之和大于其前21项之和，则（）A．d＜0 B．d＞0 C．a16＜0 D．a16＞0【考点】85：等差数列的前n项和．【分析】由｛a n｝的前10项之和大于其前21项之和，得到a1＜﹣15d，由此得到a16=a1+15d＜0．【解答】解：等差数列{a n}的公差为d，d≠0，∵｛a n｝的前10项之和大于其前21项之和，∴10a1+＞21a1+d，∴11a1＜﹣165d，即a1＜﹣15d,∴a16=a1+15d＜0．故选:C．【点评】本题考查命题真假的判断，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．15．如图，N、S是球O直径的两个端点，圆C1是经过N和S点的大圆，圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆，圆C1和C2交于点A、B，圆C1和C3交于点C、D，设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长，则a、b、c的大小关系为（)A．b＞a=c B．b=c＞a C．b＞a＞c D．b＞c＞a【考点】L*:球面距离及相关计算．【分析】分别计算a，b，c,即可得出结论．【解答】解：设球的半径为R，球心角∠COD=2α，则b=πR，a=2αR,∵CD＜AB,∴c＜b,∵CD=2Rsinα，∴c=2πRsinα，∵0＜α＜，∴=＞1，∴c＞a,∴b＞c＞a,故选D．【点评】本题考查球中弧长的计算，考查学生的计算能力，正确计算是关键．16．对于定义在R上的函数f(x）,若存在正常数a、b,使得f(x+a)≤f（x）+b对一切x∈R均成立，则称f(x）是“控制增长函数"，在以下四个函数中：①f（x）=x2+x+1；②f（x）=；③f（x)=sin(x2)；④f（x）=x•sinx．是“控制增长函数"的有(）A．②③B．③④C．②③④D．①②④【考点】3T:函数的值．【分析】假设各函数为“控制增长函数",根据定义推倒f（x+a）≤f(x）+b恒成立的条件，判断a，b的存在性即可得出答案．【解答】解：对于①，f(x+a)≤f（x）+b可化为:（x+a)2+（x+a）+1≤x2+x+1+b，即2ax≤﹣a2﹣a+b，即x≤对一切x∈R均成立，由函数的定义域为R,故不存在满足条件的正常数a、b,故f（x)=x2+x+1不是“控制增长函数";对于②,若f（x）=是“控制增长函数”，则f（x+a）≤f（x）+b可化为:≤+b,∴｜x+a｜≤｜x|+b2+2b恒成立，又｜x+a｜≤|x｜+a，∴|x|+a≤|x|+b2+2b，∴≥，显然当a＜b2时式子恒成立,∴f（x）=是“控制增长函数”;对于③，∵﹣1≤f（x）=sin（x2）≤1，∴f（x+a)﹣f（x）≤2，∴当b≥2时，a为任意正数,使f（x+a）≤f（x）+b恒成立，故f（x）=sin（x2）是“控制增长函数”；对于④，若f（x）=xsinx是“控制增长函数”，则（x+a）sin（x+a）≤xsinx+b恒成立，∵（x+a）sin（x+a)≤x+a,∴x+a≤xsinx+b≤x+b,即a≤b，∴f（x）=xsinx是“控制增长函数"．故选C．【点评】本题考查了新定义的理解，函数存在性与恒成立问题研究，属于中档题．三、解答题17．（14分)（2017•杨浦区二模）如图,正方体ABCD﹣A1B1C1D1中，AB=4,P、Q 分别是棱BC与B1C1的中点．(1）求异面直线D1P和A1Q所成角的大小；（2）求以A1、D1、P、Q四点为四个顶点的四面体的体积．【考点】LF：棱柱、棱锥、棱台的体积；LM：异面直线及其所成的角．【分析】（1）以D为原点，DA,DC，DD1为x，y,z轴,建立空间直角坐标系,利用向量法能求出异面直线D1P和A1Q所成角．（2）以A1、D1、P、Q四点为四个顶点的四面体的体积V=．【解答】解：（1）以D为原点，DA，DC，DD1为x,y，z轴，建立空间直角坐标系，则D1（0，0，4），P（2，4，0）,A1（4,0,4）,Q（2，4,4），=(2，4，﹣4)，=(﹣2,4,0）,设异面直线D1P和A1Q所成角为θ，则cosθ===，∴θ=arccoa．∴异面直线D1P和A1Q所成角为arccos．(2）∵==8，PQ⊥平面A1D1Q，且PQ=4,∴以A1、D1、P、Q四点为四个顶点的四面体的体积:V===．【点评】本题考查异面直线所成角的求法，考查四面体的体积的求法，是中档题,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想．18．（14分）（2017•杨浦区二模）已知函数f（x）=．(1）判断函数f(x）的奇偶性，并证明；（2）若不等式f（x）＞log9(2c﹣1）有解,求c的取值范围．【考点】3K：函数奇偶性的判断．【分析】（1）利用奇函数的定义，即可得出结论；(2）f（x）===﹣+∈（﹣，），不等式f（x）＞log9（2c﹣1）有解,可得＞log9（2c﹣1），即可求c的取值范围．【解答】解：(1）函数的定义域为R，f（x）==,f（﹣x）==﹣f（x），∴函数f(x）是奇函数；（2）f（x）===﹣+∈（﹣,）∵不等式f（x）＞log9（2c﹣1）有解,∴＞log9（2c﹣1），∴0＜2c﹣1＜3,∴．【点评】本题考查奇函数的定义，考查函数的值域，考查学生分析解决问题的能力,属于中档题．19．（14分）（2017•杨浦区二模）如图，扇形ABC是一块半径为2千米，圆心角为60°的风景区，P点在弧BC上，现欲在风景区中规划三条商业街道，要求街道PQ与AB垂直，街道PR与AC垂直,线段RQ表示第三条街道．（1）如果P位于弧BC的中点,求三条街道的总长度；（2)由于环境的原因，三条街道PQ、PR、RQ每年能产生的经济效益分别为每千米300万元、200万元及400万元，问：这三条街道每年能产生的经济总效益最高为多少？（精确到1万元）【考点】HU：解三角形的实际应用；HS：余弦定理的应用．【分析】（1）由P为于∠BAC的角平分线上，利用几何关系，分别表示丨PQ 丨,丨PR丨，丨RQ丨，即可求得三条街道的总长度；(2）设∠PAB=θ，0＜θ＜60°,根据三角函数关系及余弦定理，即可求得丨PQ丨,丨PR丨，丨RQ丨，则总效益W=丨PQ丨×300+丨PR丨×200+丨RQ丨×400，利用辅助角公式及正弦函数的性质,即可求得答案．【解答】解：(1）由P位于弧BC的中点,在P位于∠BAC的角平分线上，则丨PQ丨=丨PR丨=丨PA丨sin∠PAB=2×sin30°=2×=1,丨AQ丨=丨PA丨cos∠PAB=2×=，由∠BAC=60°,且丨AQ丨=丨AR丨,∴△QAB为等边三角形，则丨RQ丨=丨AQ丨=,三条街道的总长度l=丨PQ丨+丨PR丨+丨RQ丨=1+1+=2+；(2）设∠PAB=θ，0＜θ＜60°，则丨PQ丨=丨AP丨sinθ=2sinθ，丨PR丨=丨AP丨sin（60°﹣θ）=2sin（60°﹣θ）=cosθ﹣sinθ,丨AQ丨=丨AP丨cosθ=2cosθ,丨AR丨=丨AP丨cos（60°﹣θ）=2cos（60°﹣θ）=cosθ+sinθ由余弦定理可知：丨RQ丨2=丨AQ丨2+丨AR丨2﹣2丨AQ丨丨AR丨cos60°, =(2cosθ）2+（cosθ+sinθ)2﹣2×2cosθ（cosθ+sinθ）cos60°，=3,则丨RQ丨=,三条街道每年能产生的经济总效益W，W=丨PQ丨×300+丨PR丨×200+丨RQ 丨×400=300×2sinθ+（cosθ﹣sinθ）×200+400=400sinθ+200cosθ+400，=200（2sinθ+cosθ)+400，=200sin(θ+φ）+400,tanφ=,当sin（θ+φ）=1时，W取最大值，最大值为200+400≈1222,三条街道每年能产生的经济总效益最高约为1222万元．【点评】本题考查三角函数的综合应用，考查余弦定理,正弦函数图象及性质，辅助角公式，考查计算能力,属于中档题．20．（16分）（2017•杨浦区二模）设数列{a n｝满足a n=A•4n+B•n,其中A、B是两个确定的实数，B≠0．(1)若A=B=1，求｛a n}的前n项之和；（2)证明:{a n}不是等比数列;（3）若a1=a2，数列{a n}中除去开始的两项之外,是否还有相等的两项？证明你的结论．【考点】8E:数列的求和；8H：数列递推式．【分析】（1)运用数列的求和方法：分组求和，结合等比数列和等差数列的求和公式，计算即可得到所求和；（2）运用反证法，假设{a n}是等比数列，由定义，设公比为q，化简整理推出B=0与题意矛盾,即可得证；(3）数列{a n}中除去开始的两项之外,假设还有相等的两项，由题意可得B=﹣12A，构造函数f（x）=4x﹣12x，x＞0，求出导数和单调性，即可得到结论．【解答】解：（1）由a n=4n+n，可得{a n｝的前n项之和为（4+42+…+4n）+（1+2+…+n）=+n（n+1）=(4n﹣1）+（n2+n）；（2）证明：假设｛a n｝是等比数列，即有=q(q为公比),即为Aq•4n+Bq•n=A•4n+1+B•（n+1），即Aq=4A，Bq=B，B=0，解得q=4，B=0，这与B≠0矛盾,则{a n}不是等比数列；（3）若a1=a2,数列{a n｝中除去开始的两项之外，假设还有相等的两项，设为a k=a m,（k，m不相等），由a1=a2，可得4A+B=16A+2B,即B=﹣12A．则a n=A•4n+B•n=A（4n﹣12•n)，即有A(4k﹣12•k)=A（4m﹣12•m),即为4k﹣12•k=4m﹣12•m，构造函数f（x）=4x﹣12x，x＞0，f′(x)=4x ln4﹣12,由f′（x)=0可得x0=log4∈(1，2),当x＞x0时,f′（x）＞0,f（x）递增，故数列{a n}中除去开始的两项之外，再没有相等的两项．【点评】本题考查数列的求和方法:分组求和,考查等比数列和等差数列的求和公式，同时考查反证法的运用，以及构造函数法,考查化简整理的运算能力,属于中档题．21．(18分）（2017•杨浦区二模）设双曲线Γ的方程为x2﹣=1，过其右焦点F且斜率不为零的直线l1与双曲线交于A、B两点，直线l2的方程为x=t，A、B 在直线l2上的射影分别为C、D．（1)当l1垂直于x轴，t=﹣2时，求四边形ABDC的面积；（2)当t=0，l1的斜率为正实数，A在第一象限，B在第四象限时,试比较和1的大小，并说明理由；（3）是否存在实数t∈（﹣1,1），使得对满足题意的任意直线l1，直线AD和直线BC的交点总在x轴上，若存在，求出所有的t的值和此时直线AD与BC交点的位置；若不存在，说明理由．【考点】KC：双曲线的简单性质．（1）由双曲线Γ的方程为x2﹣=1,可得c==2,可得右焦点F（2,0）．当【分析】l1垂直于x轴，t=﹣2时,由双曲线的对称性可得：四边形ABDC为矩形．即可得出面积．（2)作出右准线MN：x=．e==2．分别作AC⊥MN,垂足为M；BD⊥MN，垂足为N．利用双曲线的第二定义可得：=,==．（3)存在实数t∈(﹣1,1),t=时,定点．下面给出证明分析：设直线AB的方程为：y=k(x﹣2）,A（x1，k（x1﹣2）），B（x2，k（x2﹣2))．则C（t，k（x1﹣2）），D（t,k（x2﹣2）)．直线方程与双曲线方程联立化为：（3﹣k2）x2+4k2x ﹣4k2﹣3=0，分别得出:直线AD与BC的方程，进而得出．【解答】解：（1）由双曲线Γ的方程为x2﹣=1，可得c==2，可得右焦点F(2，0)．当l1垂直于x轴，t=﹣2时，由双曲线的对称性可得：四边形ABDC为矩形．代入双曲线可得：22﹣=1，焦点y=±3．∴四边形ABDC的面积S=4×6=24．(2）作出右准线MN：x=．e==2．分别作AC⊥MN，垂足为M；BD⊥MN，垂足为N．则==+．===．∵｜AF｜＞｜FB|，∴＜．∴＜1．（3)存在实数t∈（﹣1，1），t=时，定点．下面给出证明:设直线AB的方程为：y=k（x﹣2）,A(x1，k（x1﹣2）），B（x2，k（x2﹣2））．则C（t，k（x1﹣2）），D（t，k（x2﹣2)）．联立，化为：（3﹣k2）x2+4k2x﹣4k2﹣3=0，可得x1+x2=，x1•x2=．直线AD的方程为:y﹣k(x1﹣2）=(x﹣x1），令y=0，解得x=．直线BC的方程为：y﹣k（x2﹣2)=（x﹣x2）,令y=0，解得x=．由=，可得：（2+t）（x1+x2)﹣2x1•x2﹣4t=0．∴（2+t）•﹣2•﹣4t=0．化为:t=，不妨取k=1，则2x2+4x﹣7=0,解得x=．不妨取x1=，x2=．定点的横坐标x===．∴定点坐标．【点评】本题考查了双曲线的第二定义、直线与双曲线相交问题、一元二次方程的根与系数的关系、直线过定点问题，考查了推理能力与计算能力，属于难题．。

二年级下册数学第七单元同步练习4班级：学号：姓名：家长签名：成绩1.数位顺序表中，从右边起，第二位是（）位，第三位是（）位，个位是第（）位，第（）位是万位，第四位是（）位。

2.（1）在5099的后面连续数出3个数：（）、（）、（）。

（2）6900的相邻数是（）和（）。

3.（1）4135是( )位数，最高位是（）位，它是由( )个千、( )个百、( )个十和( )个一组成的。

（2） 5个千和1个十组成的数是（）。

（3） 6个千和7个一组成的数是（）。

（4）一个数的千位和个位上是5，其余各位上都是0，这个数是( )。

4. （1） 36个十是( )， 22个百是( )，10个一千是( )。

（2）520里有( )个十，3900里有( )个百。

5.（1）最大的四位数是（），最小的四位数（），它们相差( )。

（2）比9999多1的数是（）。

6. 读出下面各数。

2017 6003 89007. 写出下面各数。

五千零九十七千零四一万8.把下面各数按照从大到小的顺序排列。

650、 6500、 6005、 506、 5060。

( )>( )>( )>( )>( )。

9.（1）红星电影院有3928个座位，约是（）个。

（2）果园里有桃树589棵,约是（）棵，梨树1090棵，约是（）棵。

10.书店一共进了1000本《故事大王》，上周卖了470本，这周卖了280本。

还剩多少本？答：还剩（）本。

11.果园里有800棵桃树，200棵梨树，一共有多少棵树？答：一共有（）棵树。

12.水果店运进350箱苹果，运进的香蕉比苹果少80箱。

运进苹果和香蕉一共有多少箱？答：运进苹果和香蕉一共有（）箱。

13.图书室有故事书3850本，科技书2006本，童话书1899本，三种书大约一共多少本？答：三种书大约一共（）本。

14.一台风扇487元，一个电饭煲532元，妈妈带1000元够吗？答：妈妈带1000元（）。

二年级数学下册解决问题训练题1、一辆空调车上有42人，中途下车8人，又上来16人，现在车上有多少人?2、面包房一共做了54个面包，第一队小朋友买了8个，第二队小朋友买了22个，现在剩下多少个?3、3个组一共收集了94个易拉罐，其中第一组收集了34个易拉罐，第二纽收集了29个易拉罐。

那第三小组收集了多少个易拉罐?4．新型电脑公司有87台电脑，上午卖出1 9台，下午卖出26台，还剩下多少台?(用两种方法解答)5．班级里有22张腊光纸，又买来27张。

开联欢会时用去38张，还剩下多少张?6．少年宫新购进小提琴52把，中提琴比小提琴少20把，两种琴一共有多少把?7．一辆公共汽车里有36位乘客，到福州路下去8位，又上来12位，这时车上有多少位?8、甲数是20，乙数比甲数多5，乙数是多少？9、有25个苹果，梨比苹果少7个，有多少个梨？10、小青有28张画片，照片比画片多16张。

小青有多少张照片？11、男生有35人，男生比女生多2人，女生有多少人？12、男生有35人，男生比女生少2人，女生有多少人？13、动物园有20只黑熊，黑熊比白熊多8只，白熊有多少只？14、动物园有20只黑熊，白熊比黑熊多8只，白熊有多少只？15、红领巾养鸡场有公鸡44只，母鸡比公鸡多16只。

母鸡有多少只？16、红领巾养鸡场有母鸡60只，母鸡比公鸡多14只，公鸡有多少只？17、红领巾养鸡场有母鸡60只，公鸡比母鸡少14只，公鸡有多少只？18、红领巾养鸡场有公鸡44只，公鸡比母鸡少16只。

母鸡有多少只？19、上手工课，一班节约了15张纸，二班比一班多节约了8张纸。

二班节约了多少张纸？20、上手工课，一班节约了15张纸，比二班多节约了8张。

二班节约了多少张纸？21、书架上的故事书比连环画少15本，书架上有杂志8本，有故事书32本。

连环画有多少本？故事书和连环画一共有多少本？22、小明的妈妈买回来一根16米长的绳子，截去一些做跳绳，还剩6米，做跳绳用去多少米？23、二年级的男同学有35人，女同学有37人，一共有多少人？其中有50人参加了今年暑假的“红色之旅”活动，有多少人没有参加“红色之旅”活动？24、停车场上有65辆小汽车，开走了31辆，还剩下多少辆？又开来6辆。

2017数学二真题一、选择题（每小题4分，共32分） （1）若函数21cos ,0(),0xx f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续，则（ ）。

A. 12ab =B. 12ab =-C. 0ab =D. 2ab =【答案】A【解析】由连续的定义可知：-00lim ()lim ()(0),x x f x f x f +→→==其中-0(0)lim ()x f f x b →==，2000112lim ()lim lim 2x x x f x ax a+++→→→===，从而12b a =，也即12ab =，故选A.【试题点评】本题考查函数的连续性。

此知识点在冲刺阶段的数学冲刺串讲班中第一部分高等数学有重点讲解，在强化阶段数学强化班高等数学第一章函数、极限、连续和强化阶段数学重点题型精讲班也均有涉及。

（2）设二阶可导函数()f x 满足(1)(1)1,(0)1f f f =-==-，且''()0f x >，则（ ）。

【答案】D【解析】limsin )sin nn x x x a a→∞+=+（，而要使sin 0a a +=，只有a=0，故D 正确。

【试题点评】本题考查级数收敛性。

此知识点在冲刺阶段的数学冲刺串讲班中第一部分高等数学有重点讲解，在强化阶段数学强化班高等数学第九章级数和强化阶段数学重点题型精讲班也均有涉及。

（4）微分方程()'''2481cos2xy y y e x -+=+的特解可设为ky=（ ）。

A. ()22cos2sin2xx Aee B x C x ++ B. ()22cos2sin 2xx Axe e B x C x ++ C. ()22cos2sin 2xx Aexe B x C x ++ D. ()22cos2sin 2xx Axexe B x C x ++【答案】C【解析】齐次方程的特征根为22r i =±，原方程可分解为两个非齐次方程：2''4'8xy y y e -+=和2''4'8cos2x y y y e x-+=，可知第一个方程的特解为2xAe ，第二个方程的特解为2(cos2sin 2)xxeB xC x +，故选C.【试题点评】本题考查微分方程的解。

二年级数学下册第四单元生活中的大数检测试卷一、读出下面各数。

5632 读作: 9096 读作: 3030 读作: 7003 读作: 6400 读作: 1230读作: 1111 读作: 9990 读作: 2097读作:二、选择题。

把下面正确答案序号填在括号里。

1.601.106.600这三个数中, ...）最小.A.60.....B.10.....C.6002.605.650、600这三个数中, ...）最大.A.60.....B.65.....C.6003.比最大的三位数多1的数是... ）. A、99.....B、100.... C、11004.一个四位数，千位上和个位上都是1，其它数位上都是0，这个数是... ）。

A.1010B.1001C.11005.读数时, 中间有两个零...）. A、都要读出. B.都不读出..C.只读一个零6.最大的四位数是... ）.A.100.....B.998......C.99997.五千零五十五写作... ）.A.505.....B.555...... C.50558.与10000最近的数是.... ）. A.999.... B.100...... C.90009.用两个0, 两个4组成的四位数中, 不读出0个是.. ）. A.440.B、400.C、404010.9998的近似数是... . A、999..... B、1000..... C、9000三、判断题, 在对的（）里画“√”, 错的画“×”。

1.一千是由十个千组成................... ）2.写八百时, 先要写8, 再在后面写2个0....... ... ）3.五百零四, 写作54................ ... ）4.609读作六百九十.................... ）5.一千零一写.101................ ... ）6.最大的两位数是999................... ）7.2010读作二千零一................ ... ）8.一个四位数最高位是万位................. ）9.读数时, 数的末尾不管有几个0, 都不读.......... ）10.从左边起万位在第四位.............. ... ）四、按要求数出下面各数。

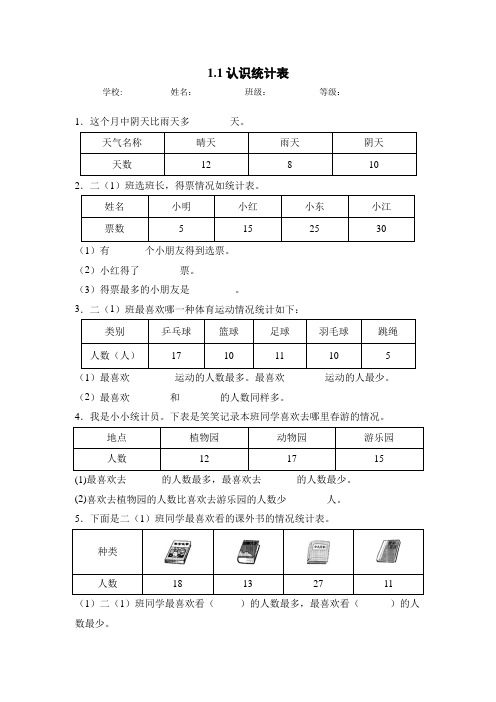
1.1认识统计表学校:___________姓名：___________班级：___________等级：___________ 1．这个月中阴天比雨天多________天。

天气名称晴天雨天阴天天数12 8 102．二（1）班选班长，得票情况如统计表。

姓名小明小红小东小江票数 5 15 25 30（1）有_______个小朋友得到选票。

（2）小红得了________票。

（3）得票最多的小朋友是_________。

3．二（1）班最喜欢哪一种体育运动情况统计如下：类别乒乓球篮球足球羽毛球跳绳人数（人）17 10 11 10 5 （1）最喜欢_________运动的人数最多。

最喜欢________运动的人最少。

（2）最喜欢________和________的人数同样多。

4．我是小小统计员。

下表是笑笑记录本班同学喜欢去哪里春游的情况。

地点植物园动物园游乐园人数12 17 15(1)最喜欢去_______的人数最多，最喜欢去_______的人数最少。

(2)喜欢去植物园的人数比喜欢去游乐园的人数少________人。

5．下面是二（1）班同学最喜欢看的课外书的情况统计表。

种类人数18 13 27 11 （1）二（1）班同学最喜欢看（）的人数最多，最喜欢看（）的人数最少。

（2）最喜欢看《寓言故事》的有（）人。

（3）最喜欢看《少儿百科》的比最喜欢看《故事大王》的多（）人。

（4）最喜欢看《寓言故事》和最喜欢看《唐诗三百首》的共有多少人？6．下面是家家乐超市一天内销售饮料数量的统计情况。

（1）________卖出的最多，________卖出的最少。

（2）一天内一共卖出________瓶饮料。

（3）根据调查的结果，超市应多进哪种饮料?为什么?7．这是某电脑公司一周销售情况统计表。

（1）（）天销售量最多；（）天销售量最少。

相差（）台。

（2）周二、周四、周六三天共销售多少台？（3）按你的推测，下周哪几天销售量可能较大？（4）你还能提出什么数学问题？并解答。

《平均分》习题
一、先用6根小棒摆一摆，再填空。

（1）每2根一份，可以分成（）份。

（2）每3根一份，可以分成（）份。

二、你能按要求圈一圈，填一填吗？
（1）☆☆☆☆
☆☆☆☆
8颗☆，每4颗一份，分成了（）份。

（2）☆☆☆☆
☆☆☆☆
8颗☆，每2颗一份，分成了（）份。

（3）□ □ □ □ □ □ □ □ □
□ □ □ □ □ □ □ □ □
（）个□，每（）个一份，分成了（）份。

三、先想一想怎么分，再填空。

（1）16个桃子，每只猴子吃2个，可以分给（）只猴子吃。

（2）16个桃子，每只猴子吃4个，可以分给（）只猴子吃。

（3）16个桃子，每只猴子吃8个，可以分给（）只猴子吃。

（4）6棵松树，每2棵种一排，可以种（）排。

（5）10个○，每5个可以拼成图形五环，能拼成（）个。

四、分一分。

第二题：圈一圈，分一分。

把（）个苹果，平均分成2份，每份（）个。

把（）个苹果，平均分成3份，每份（）个。

把（）个苹果，平均分成6份，每份（）个。

《混合运算》同步测试1．脱式计算。

12－8÷4 2＋6×9 8×7－28 12＋8×6考查目的：掌握含有两级运算的运算顺序，熟悉脱式计算的书写格式。

答案：10 56 28 60 （脱式计算过程略）解析：这类题学生首先要思考题目属于那种类型，从而正确运用相应的运算顺序进行计算。

2．下面的计算对吗？如果不对，把它改正过来。

2＋4×7 14－4÷2=6×7 =10÷2=42 =5考查目的：熟练掌握含有两级运算的运算顺序，并正确计算。

答案：2＋4×7 14－4÷2=2+28 =14-2=30 =12解析：这是一道判断改错题，相对于直接运用运算顺序进行计算的要求更高些。

对初学者有一定误导性，训练时要注意引导学生细致分析和思考。

3．在里填上“>”“<”或“=”。

40÷5－7 7 7＋2×8 5＋167÷1＋7 16－16÷8 72÷9＋75 8＋9×9考查目的：熟练掌握含有两级运算的运算顺序，并会比较大小。

答案：< > = <解析：这是在正确进行综合算式计算后进行比较大小的扩展训练，难度稍高，注意解决方法的灵活性。

4．先填空，再列综合算式。

考查目的：要求学生根据计算过程列出综合算式。

答案：63÷9 +20 8-8÷2=7+20 =8-4=27 =4解析：本题突出有两级运算时，先算乘、除法，不必使用小括号。

5．看图列式计算。

考查目的：考查学生看图理解数量关系，列出综合算式的能力。

答案：8×4＋10=42或8×5+2=42解析：本题注重学生的读图能力训练，答案不唯一。

6．小红在算 18－÷2时弄错了运算顺序，先算减法后算除法了，结果得数是5。

正确的得数应该是多少？考查目的：巩固混合运算的运算顺序，学会逆向思维。

部编版二年级下册数学全册同步练习(一课一练)说明本文档是针对部编版二年级下册数学全册同步练所做的总结和补充。

通过这些练题，学生可以巩固和提升他们在数学方面的知识和能力。

内容本册练题共包括多个单元，每个单元都有一课一练的练题目。

以下是各个单元的简介：1. 数的认识：这一单元主要介绍了数字的认识和写法，包括自然数、零以及正整数的概念。

练题中有一些填写数字的题目，帮助学生熟悉数字的书写。

2. 数的比较：这一单元教授了数字的比较方法，包括大于、小于、等于等概念的理解。

练题中，学生需要根据给定的数字判断大小关系，并填写正确的符号。

3. 数的计数：这一单元教授了数字的计数方法，包括顺序填数、用数棒表示数目等。

练题中，学生需要填写正确的数字来完成计数题目。

4. 两位数的认识：这一单元主要介绍了两位数的概念和构成，包括十位和个位的认识。

练题中，学生需要根据给定的数字写出它们的十位和个位数字。

5. 两位数的拆解与组成：这一单元教授了两位数的拆解与组成方法，包括十位和个位的划分和组合。

练题中，学生需要将给定的数字进行拆解和组合，并填写正确的数字。

6. 加法与减法：这一单元主要教授了加法和减法运算的基本概念和方法，包括进位与退位等。

练题中，学生需要进行简单的加法和减法计算，并填写结果。

7. 变化量：这一单元教授了变化量的概念和计算方法，包括增加和减少的数量。

练题中，学生需要计算给定数字的增加和减少量，并填写结果。

8. 位置与方向：这一单元主要介绍了位置和方向的基本概念，包括左右、前后等方向的认识。

练题中，学生需要根据给定的方向进行位置判断和描述。

通过完成这些练题，学生能够巩固和提升他们在数学方面的知识和能力，从而更好地应对日常研究和课堂考试。

结束语部编版二年级下册数学全册同步练习提供了丰富的练习题目，帮助学生巩固和提升他们在数学方面的能力。

通过认真学习和完成这些练习题，学生将能够更好地理解和掌握数学知识，为进一步学习打下坚实的基础。

800＋300＝8000＋500＝1000－100＝7×2＋12＝500＋500＝60×9＝9×(52－45)＝42÷2÷3＝300－10＝130－20＝3×2＝42＋7×6＝1200＋500＝50×7＝3×(51－46)＝42÷2÷3＝560－200＝12×3＝32÷8＝73＋49÷7＝800＋80＝24÷4＝90×8＝6×(1＋3)＝100＋50＝14÷2＝30×3＝6×(2＋1)＝1300＋100＝10×8＝9×(54－48)＝30÷2÷3＝600＋20＝4÷1＝90×6＝7×(5＋2)＝1800＋300＝80×5＝6×(55－49)＝30÷2÷3＝500＋900＝5000＋900＝6000－600＝4×5＋19＝900－20＝130－20＝7×8＝21＋4×2＝妈妈买来6袋苹果，每袋10个。

吃去9个，还剩多少个？200＋400＝80×7＝9×(51－50)＝54÷2÷3＝1300＋300＝60×3＝4×(51－50)＝60÷2÷3＝200＋200＝3700＋700＝3000－600＝6×2＋24＝520－300＝38×1＝40÷8＝76＋50÷5＝300＋300＝5600＋300＝6000－700＝1×4＋24＝800＋100＝5100＋200＝9000－200＝2×5＋15＝400＋90＝72÷8＝50×9＝8×(2＋3)＝400＋600＝4300＋700＝7000－400＝3×8＋21＝700＋20＝30÷5＝50×6＝5×(4＋5)＝700＋70＝4÷1＝70×2＝9×(4＋3)＝1300＋900＝30×8＝2×(55－47)＝30÷2÷3＝600＋900＝50×3＝9×(52－49)＝30÷2÷3＝800＋90＝15÷5＝50×9＝5×(2＋3)＝500＋600＝8500＋600＝7000－800＝3×6＋14＝530－300＝32×1＝25÷5＝53＋21÷1＝570－200＝13×2＝15÷5＝37＋6÷1＝900－10＝160－40＝4×8＝22＋2×4＝700－20＝170－70＝5×4＝42＋4×3＝700＋40＝25÷5＝50×1＝4×(2＋2)＝300－10＝170－50＝7×7＝34＋4×5＝新华校办厂生产玩具，张师傅做了186个，李师傅比张师傅多做26个，王师傅比李师傅少做11个，王师傅做玩具多少个？妈妈买来8袋苹果，每袋7个。