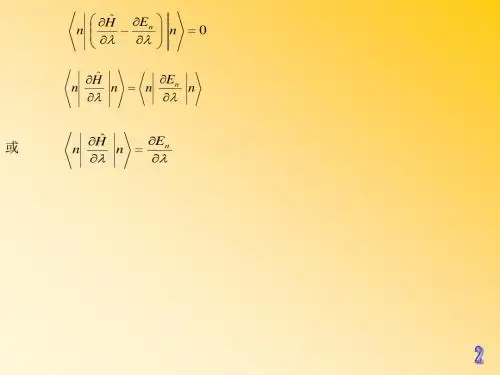§2.8维里定理

格式：ppt
大小：218.00 KB
文档页数：5

下载文档原格式

5维里定理

φn )
=
En (φn ,
∂ ∂λ
φn )
再按假设 (φn ,φn ) = 1，所以有
(φn
,
( ∂H
∂λ
)φn
)
=
∂En
∂λ
定理得证。
（二）维里定理：
当体系在定态时，粒子处于势场V (r) 中。
设哈密顿算符为
H
=
1 2µ
P2
+V (r) ，
设φn 未归一化的束缚态波函数，则有：
< φn
|
1
2µ
P2
2m
∂p 2m
⒁
H 和 H0 的区别，除常数项外，无非是 p 换成 P
点对能级没有影响。由此可知
，后面这一
En
=
E(0) n
−
λ2
2m
⒂
例题 5:粒子在对数函数势场中运动，
V (r) = C ln( r ), r0
C， r0 >0
r C， 0 为与质量无关之常数，试证明：（a）各束缚态动能平
均值相等。（b）能量间距与粒子质量无关。
>
上述是维里定理得两种不同的证明方法，现在我们来讨论一下
维里定理的一种特例
当V (r) 是 x,y,z 的 n 次齐次函数（即V (cx, cy, cz) = cnV (x, y, z) ，c 是常数）时，求势能与动
能平均值的关系。
有已知条件，我们知道
r.∇V (r) = nV (r)
由维里定理得
维里定理
一：定理证明
（一）Hellman—Feynman 定理：
设体系的哈密顿量 H 中含有某参量 λ ， En 为 H 的本征值。相

几个定理

(2)
若 ( ) 为实数，则有：

| |
| H | | H |
(2)简化为
H | 2 | | | 2 | H |
$6-1 海尔曼-费曼定理和维里定理
一海尔曼-费曼定理
20世纪30年代末，Hellmann 和 Feynman 分别提出一个定理，现统称为Hellmann－ Feynman 定理。

在玻恩-奥本海默近似下，电子运动的哈密顿算符 H ，波函数
能量E等都是核间矩R的函数，或者说是以R为参数。推广一下， H ( ) ( ) E ( ) 以为参数，可以是核间矩，核电荷、力常数等。则有：
是一个-3次的齐函数，因为有
f ( sx, sy, sz ) s 3 [
1 1 1 x 3 ] s f ( x, y, z ) 3 3 3 2 2 x y z y z
(2)齐次函数的欧拉定理：如果
f ( x1 , x2 ,, x j )
为n次齐函数，则
f xk nf xk k
q2 ， q3
；相应的动量分量为
p1
p ， 2 ，
i
p3
）。所以
[ H , A] [ H , qi pi ] [ H i , qi pi ] qi [ H i , pi ] [ H i , qi ] pi
i i i
若选择为第P个核的坐标，则有
பைடு நூலகம்E PE
H | | | PV | | FP |
P E | FP |

费曼-海尔曼定理

,
T n lT ˆmnld m rE n
论文的结构和主要内容
上面的具体计算十分复杂，但是如
果用维里定理，问题就十分容易了。根
据题意我们可以知道势能是的 n 1齐次
函数，所以
2T U
,
又因为总能量 EnTUT,
因此
U2T2En .
即平均势能为负值，并且为总能量
的两倍，由于平均动能一定是负值，这
论文的结构和主要内容
3.1.2示例对比分析
在求解一维谐振子问题中的 x 2 、p 2 ，
n
n
以及 xp 时，如果利用量子力学中求期
望值的方法，那么，我们就要将已知的
哈密顿量带入到线性谐振子的本征函数，
即
1
nx1 22nn!2e1 22x2Hnx,
m
令，Hˆ mx2 ，此处利用费曼海尔曼定
理，就可以得到
E nn1 2mx2 n
对上式化简得
x2 n n12m
论文的结构和主要内容
3.2费曼-海尔曼定理解氢原子中一些问题 3.2.1典型示例的选取
在量子力学中，由于氢原子问题有解析解，更简单、更实用，因此它的应用十分广泛、重要。所以，在此选择它作为示例。
费曼-海尔曼定理和维里定理的应用
提纲
一选题的目的、意义和要完成的任务二论文的基本框架和主要内容三完成论文写作存在的问题及收获
一、选题的目的、意义和要完成的任务
费曼-海尔曼定理和维里定理的应用极其广泛, 在量子力学中，处理问题也十分简便，可惜在各种教材中, 只是轻轻带过, 很少充分论述。
论文的结构和主要内容
4.2库仑场问题
若库仑场势能为，如 Ures2

模的Krull维数定理

证明：1.令G(A)
=
⊕
n
Qn/Qn+1，G(M )
=
⊕
n
Mn/Mn+1。G0(A)
=
A/Q是Artin局
部环；G(A)是N orther环，G(A)是有限生成分次G(A)− 模。
每个Gn(M ) = Mn/Mn+1是被Q所零化的N ortherA−模，因此是N ortherA/Q−模，
于是有有限长度(由于A/Q是Artin环)。于是M/Mn有有限长度而
n→∞
以g, g有相同的次数和首项系数。
推论3.2 对所有大的n，长度l(A/Qn)是次数≤ s的一个多项式χQ(n)，这里s是Q的生成元的最小个数。
5
第二章局部环的维数理论
下面命题指出，多项式χQ(n)对于M−准素理想Q的不同选取都有相同的次数。命题3.3 如果A, M, Q如上给出，那么
3
第二章预备知识元。由此推出，如A是AP中的理想而A M，那么A就含一个可逆元，因而是整个环。因此，M是环AP中仅有的极大理想；换句话说，AP是局部环。从A转化到AP的过程叫做在P的局部化。
定义2.12 环A的参数系：如果x1, · · · , xd生成一个M−准素理想，且d = dimA，我们就把x1, · · · , xd叫作环A的一个参数系。
∑n
ln = l(M/Mn) = l(Mr−1/Mr)
(1)
r=1
2. 如果x1, · · · , xs生成Q，那么G(A)作为A/Q−代数由xi在Q/Q2中的象xi的次
数为1。则有l(Mn/Mn+1) = f (n)，
对所有大的n，而f (n)是n的次数≤ s−1的多项式，由(1)我们有ln+1−ln = f (n)，

理论力学课程教学大纲.

《理论力学课程》教学大纲学时：72 时学分：4 分课程类型：必修适用专业：物理学一、课程性质、地位和任务理论力学是四年制高等院校物理学专业的必修的基础课程。

本课程以牛顿运动定律为基础，高等数学为工具，通过严密的逻辑推理，全面的阐述宏观物体机械运动的基本概念和基本规律。

通过教学，应使学生：一，对宏观机械运动规律有比较全面，系统的认识，能掌握处理力学问题的一般方法，培养起一定的抽象思维和逻辑推理能力；二，能较深刻的分析力学教材，能分析生产生活中的问题；三，认识教学与物理的密切联系，能运用数学工具解决物理问题；四，通过本教材的学习为进一步学习理论物理打下了坚实的基础。

本课程总学时为72学时，讲授与习题的比例为3：1，具体情况如下。

二、课程主要内容概述及教学基本要求本课程主要内容：第一篇牛顿力学主要包括：质点力学、质点组力学、刚体力学、非惯性系力学等；第二篇分析力学主要包括：虚功原理、拉格朗日方程、哈密顿正则方程、哈密顿原理等。

理论力学是学生接触到的第一门理论物理课程。

与普通物理力学相比，它在理论上和解决问题的方法上都有较大提高。

通过本课程的学习，使学生受到理论物理研究方法的初步训练，应培养学生严密逻辑推理的能力、抽象思维的能力、从一般到特殊的分析方法及运用高等数学方法解决力学问题的能力，并较好理解数学与物理的密切关系。

三、课程内容绪论1.理论力学的研究对象和方法2.经典力学的运用方法第一章质点力学基本要求：（1）.空间和时间，力和质量，惯性参照系是经典力学的基本概念，牛顿定律是经典力学的基本定律。

它是理论力学的起点。

同时介绍现代科学的观点。

（2）.重点：1.平面坐标系和自然坐标系中速度加速度分量式的推导和应用，也是本章的难点。

2.质点运动微分方程的建立和求解。

要多举几种不同类型（F=F（r,v,t））例题，学会以高等数学为工具把物理问题转化为数学方程，并求数学表达式分析其中的物理意义，从而提高提出问题，分析问题解决问题的能力 3.要求学生明确质点的约束运动在加约束反力后，可按自由质点处理 4.由于质点的三个基本定律及守恒律在力学多半阐述过，要在原有基础上概括提高，对于一些问题要能正确判断一个力为保守力，并能求出相应的势能曲线。

物理化学主要公式定理

物理化学主要公式第一章气体的pVT 关系1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ，V ，T 及n 单位分别为Pa ，m 3，K 及mol 。

m /V V n =称为气体的摩尔体积，其单位为m 3 · mol -1。

R =8.314510 J · mol -1 · K -1，称为摩尔气体常数。

此式适用于理想气体，近似地适用于低压的真实气体。

2. 气体混合物（1）组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量。

A m,*V 表示在一定T ，p 下纯气体A 的摩尔体积。

∑*AA m ,A V y 为在一定T ，p 下混合之前各纯组分体积的总和。

（2）摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量，∑=BB n n 为混合气体总的物质的量。

上述各式适用于任意的气体混合物。

（3）V V p p n n y ///B B B B *=== 式中p B 为气体B ，在混合的T ，V 条件下，单独存在时所产生的压力，称为B 的分压力。

*B V 为B 气体在混合气体的T ，p 下，单独存在时所占的体积。

3. 道尔顿定律p B = y B p ，∑=BB p p上式适用于任意气体。

对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。

5. 范德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa · m 6 · mol -2，b 的单位为m 3 · mol -1，a 和b 皆为只与气体的种类有关的常数，称为范德华常数。

维里定理计算温度

维里定理计算温度
维里定理是一个物理学原理，用于计算气体或液体的温度。

它描述了粒子在机械混合过程中能量的分配。

维里定理的核心思想是，当两个物体接触时，会发生能量转移。

更具体的说，维里定理指出，当两个物体接触时，由于它们的不同温度而存在温度差，温度高的物体会向温度低的物体传递能量，直到能量分布在两个物体之间达到平衡状态。

按照维里定理计算温度，可以通过以下公式来表达：
T1/T2=(m2/m1)*(v2^2/v1^2)
其中，T1和T2分别是接触物体1和物体2的温度，m1和m2分别是物体1和物体2的质量，v1和v2分别是物体1和物体2的速度。

这个公式的实质是，两个物体之间的热传递速率与它们的相对速度成正比，而与它们的质量平方成反比。

在计算过程中，需要确定物体之间的相对速度和质量，然后利用公式计算出它们之间的温度差。

维里定理对于实际的热传递问题非常有用，可以帮助科学家和工程师设计更高效的热交换系统。

它也被用于研究气体和液体的热力学性质，以及许多其他领域的研究。

位力定理

位力定理由上一节我们知道，力矩反映了力的切向分量对物体运动的影响，而角动量反映了物体在切向上的运动，这个直观的图像其结论就是角动量定理。

实际上，关于力的径向分量也有一个有趣的结果，这就是virial （位力）定理，它涉及的是各种力学量的时间平均值之间的关系。

考虑一个受力作用、位矢为F K r K 的粒子，它的切向运动（转动）我们已经知道是用角动量来描述的，为了描述其径向运动，我们引入下面的符号（没什么特别的名称来命名它，不过它是某个类似于转动惯量的量2I mr mr r ==⋅K K 对时间的微商）：G r p =⋅K K (1)这个量对时间的变化率不难得到 dG r p r p dt =⋅+⋅K K K K (2) 第二项中p K 就是力；而由于F K p mr=K K ，第一项两倍于粒子的动能，因此有 2dG T r F dt=+⋅K K (3) 如果对方程两边的项从时刻到时刻积分并除以1t 2t 2tt t 1Δ=−，我们就得到了在时间间隔内的平均值t Δ2112t t dG dG dt T r F dt t dt ==+Δ∫⋅K K (4) 或者把它重新写为()()212T r F G t G t t+⋅=−1⎡⎤⎣⎦ΔK K (5) 对于周期性的运动，如果我们使时间间隔t Δ恰巧等于运动的周期，上式右边的项将等于零。

即便对于非周期性的运动，如果粒子的运动总是在空间中的一个有限区域中进行的（有界运动），也就是说，粒子的坐标始终是有限的数值，那么任何时刻G 都不会取无限大，它必然有一个上限，这样当我们把式中的选的足够大，即时，方程(5)右边的项仍然是等于零的（在这里，很多书上除了假设粒子的坐标有限之外，还附加了另一个条件，即要求动量大小也是有限的。

数学上做这样的要求当然是可以理解的，但是，我们不应忘了，上面所做的一切都不过是来自Newton 定律t Δt Δ→∞F ma =K K ，而Newton 定律只有在粒子速度远远小于光速的情况下才是可以信赖的，这样的话，粒子的速度、从而其动量的数值理所当然应该是有限的。

3.5位力定理力学量守恒量及其对称性

2 2 2 ˆ ˆ ˆ p p p z ˆ ˆ [( r p ), ] [ r , z] p i z 2 m 2 m m
2 2 2 ˆ ˆ ˆ ( p p p ) ˆ p x y z ˆ [( r p ), ] i 2 m m 2
ˆ ˆ 但 [( r p ), V ( r )] r [ p , V ( r )] i r V ( r ) ？ ˆ i 2 2 2 ˆ ˆ ˆ ˆ [( r p ), H ] ( p p p ) i r V ( r ) x y z m
*ˆ E H d H
所以
因此对任意两能级 E 和 E 的差 E E 1 2 1 2 c dE dm 2 m 积分得 c E ln m n n 2 c E m l l ln 2
所以
E E n l n l
这是与m无关的常数量。
这就是数学上的 Euler 定理。
V 写成矢量的形式为将 x nV ( x ,x ,x ) i 1 2 3 x i 1 i r V nV 对此式两边求平均值，利用前面所给出的定理即得 2 T n V
3
将此式用于几个特殊情况，有（1）谐振子势 V 1 m2 x2
ˆ d 1 ˆ ˆ A A ( t ) [A , H] dt i t
则必然有
但是
ˆ,H ˆ]0 [ r p
2 ˆ p ˆ ˆ ˆ [( r p ), H ] [( r p ), V ( r )] 2 m
而
2 2 2 ˆ ˆ p p ˆ p ˆ ˆ i x [( rp ), x ] [ r , x] p 2 m 2 m m 2 2 2 ˆ p ˆy ˆy p p y ˆ ˆ i [( rp ), ] [ r , ] p 2 m 2 m m

FH定理及其应用

3
ˆ nV ˆ 2T
i 1
ˆ i2 p

xi
i 1
3
V xi
i p ˆ i xi p ˆi ) (x
i 1
3
ˆ T ˆ V 的本征函数设|m>是 H
ˆ | m E | m H m
3
m 1,2,3
ˆ nV ˆ) | m 2T nV m | (2T
i p ˆ i xi p ˆi ) | m m | (x
ˆ ˆ m | xi | l l | pi | m m | xi | l l | pi | m i 1 l
i 1 3

i | l m| x
V nV xi xi i 1
( x1 x, x2 y, x3 z)
ˆ (t ) 1 dA ˆ (t ), H ˆ (t )] [A dt i
海森堡方程：
ˆi p 1 ˆ i [ xi , H ] x i
i p
由此得到：
1 ˆ ] V ˆi , H [p i xi

1 1 2 n 3 l a 0 2
a0
e 2

2
~ 玻尔半径
（三）氢原子的径向方程
1 d 2 dR 2m e 2 l (l 1) E 2 R(r ) 0 r 2 2 r r dr dr r
数学中将满足以下关系的函数称为的m次齐次函数并有欧勒定理z的n次齐次函数所以有mf1谐振子2库仑场ex
ˆ E n H n
n 0
ˆ E n H n n n n

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 1 k 2m 1 2 mv (V ) 2 2 r 2
1 T V 2
第二章质点组力学
1. 内力的重要性质:

i 1 i j j 1
n
n
f ij 0
(i ) ri Fi ri fij 0
i j i
质点组内力的元功之和一般不能相消一对内力元功之和与参照系无关.
2. 三个定理及其守恒律 1）对固定点O (e ) dp Fi dt (e) 若 Fi 0, 则
i
(e) 则若 ri Fi M 0 dJ 0 i (e) (i ) dT Fi dri Fi dri
i i
1 2 1 T mvc mi v 'i2 柯尼希定理 2 i 2
变质量物体的运动微分方程： d (mv ) dm uF dt dt
二、若为保守力
1 T Vi ri 2 i 若单质点受有心力作用： V V (r ) ar n1
1 dV 1 1 n T r (n 1)r r (n 1)V 2 dr 2 2 1 n 2 T V 2 mv 2 k 2 m 如：圆周运动: F r r
i i
dJ M dt
(e) d rc m 2 Fi dt i mivi mvc 常矢
2
i
J 恒量
若
dW dV
(i )
(i )
dW (e) dV (e)
(i )
则T VVFra bibliotek(e)
E
2）对知心C mivi 常矢
i
(e) (e) d J ' ri Fi M ' 若 M ri Fi 0 J ' 常矢 dt i i (e) (i ) dT ' Fi dri ' Fi dri '
§2.8维里定理
一、维里定理具有统计性质——时间平均（统计力学量子力学中用到）考虑 G Pi ri , Pi mi vi i dG Pi ri Pi ri Fi ri mi ri ri Fi ri 2T dt i i i i i
1

0
dG 1 dt (G( ) G(0)) Fi ri 2T dt i
若为周期运动，则 G( ) G (0) 若非周期运动，只要 pi.ri有限，则G的上限τ取为足够长，则左端为0，所以:
1 T Fi ri 2 i
——维里定理